复变函数可导充要条件证明的另一种方法及应用

高 敏

(齐齐哈尔工程学院 基础部，黑龙江 齐齐哈尔 161005)

复变函数理论以其完美理论和精湛的技巧深入各个学科中，为航空航天、道路桥梁、通信行业的飞速发展提供了有力的技术支撑[1-4]，李晓焱、王丽颖、高喜花[5-14]等人在基础理论方面研究了复变函数的可微、解析性质等基础理论及应用进行了研究.本文在基本理论[15]的支持下，对复变函数可导充要条件进行了证明，旨在丰富复变函数理论，为判断复变函数可导提供有效的方法.

定理：设复变函数f∶G→G⟺f(x+iy)=u(x,y)+iv(x,y),f(z)在点z=x+iy可导的充要条件为u(x,y)和v(x,y)在ρ(x,y)可微且满足C-R方程

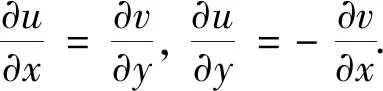
1 定理证明

1.1 必要条件

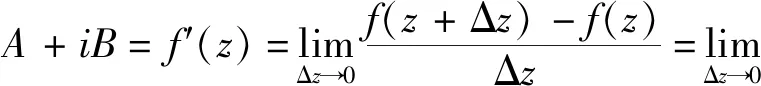
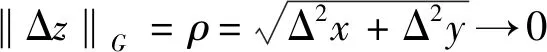
(1)+(2)可知ρ2Δv=ρ2(AΔy+BΔx)+ρ2(Δyo1(ρ2)+Δxo2(ρ2))

Δv=AΔy+BΔx+Δyo1(ρ2)+Δxo2(ρ2)

下证Δyo1(ρ2)+Δxo2(ρ2)=o(ρ)

于是 Δv=AΔy+BΔx+o(ρ)

由*方程组可知,

(3)+(4)可知-ρ2Δu=ρ2(-AΔx+BΔy)+ρ2(Δyo2(ρ2)-Δxo1(ρ2))

同理可证 Δxo1(ρ2)-Δyo2(ρ2)=o(ρ)

于是 Δu=AΔx-BΔy+o(ρ)

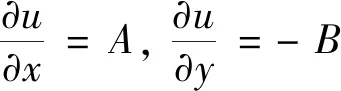
1.2 充分条件

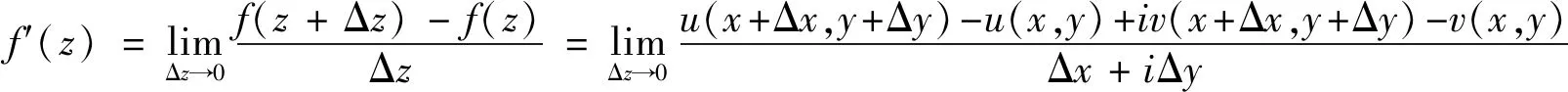
由u,v可微，于是可知

f′(z)=

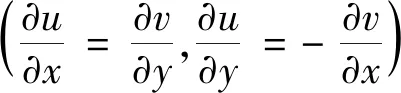
2 算例分析

例：判断f(z)=(x+y)+2yi是否可导？

解法1(定义法)：

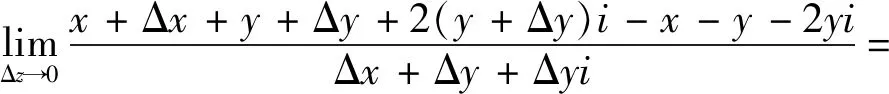
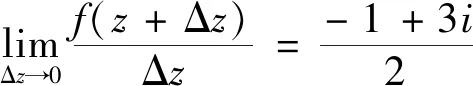
由上可知函数f(z)=(x+y)+2yi不可导

解法2

由题意可知，u=x+y,v=2y

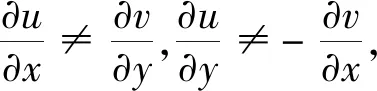
复变函数可导需满足两个条件，二者缺一不可，这两个条件也为快速判断函数是否可导提供了依据，通过对比可知,利用函数是否满足C-R方程来判断，可以大大提升判定的速度，从而可以快速判断实际问题的研究价值.