CT图像校正算法性能影响研究

李长春, 李元金

(1.滁州职业技术学院 信息工程学院，安徽 滁州 239000; 2.滁州学院 计算机与信息工程学院， 安徽 滁州 239000)

近年来，随着科技的发展，CT[1]成像系统越来越广泛地应用于临床医学领域.正常情况下，CT成像系统能够提供清晰的CT图像.但是，当投射区域含有金属等高密度物质时，重建之后的CT图像将出现从金属等高密度物质出发向四周发射的条状伪影，这就是金属伪影.这些条状伪影不仅降低了CT图像的对比度，而且使得金属等高密度物质与人体组织之间变得模糊.有时，这种伪影会阻碍医务工作者对病理的诊断，甚至阻碍了CT成像系统的应用.

为了提高CT图像的清晰度和对比度，以便提高对疾病诊断的正确率，人们提出了多种CT图像金属伪影校正方法.总体上来说，从已发表的论文可以看出，CT图像金属伪影校正方法可以分为基于硬件的CT图像金属伪影校正方法(hardware-based correction approach)和基于软件的CT图像金属伪影校正方法(software-based correction method).基于硬件的CT图像金属伪影校正方法，是CT图像出现金属伪影后最早的校正方法.在这些方法中，可以将投影前的金属等高密度物质从人体中取走，或者增加投影时的电压，但是基于硬件的校正方法不易实现，并且对人体有害，所以人们更多地求助于基于软件的CT图像金属影响校正方法.基于软件的CT图像金属伪影校正方法(software-based correction method)又可以分为基于插值的CT图像金属伪影校正方法(interpolation-based correction method)[2-10]和基于迭代的CT图像金属伪影校正方法[11-13](iteration-based correction method).受限于算法运行速度和现有CT成像系统体系结构等方面的限制，虽然有一些学者研究了基于迭代的CT图像金属伪影校正方法(iteration-based correction method)，但实践中应用甚少.相反，人们更多地求助于基于插值的CT图像金属伪影校正方法(interpolation-based correction method).

1987年，Kalender Willi A在文献[2]中首次提出了使用简单的线性插值方法校正CT图像中出现的金属伪影，这是最早的基于插值的CT图像金属伪影校正方法(interpolation-based correction method).在这之后，学者们在线性插值CT图像金属伪影校正方法的基础上对多项插值在CT图像金属伪影校正方法进行了研究.本文将在前人结果的基础上，研究多项式次数对CT图像金属伪影校正方法性能影响比较研究.

1 多项式插值校正方法

图1(A)、(B)分别显示了基于插值的CT图像金属伪影校正算法流程图.其中，图1(A)的CT图像金属伪影校正算法主要步骤如下：

1)投影数据输入；

2)CT图像重建；

3)CT图像分割和投影；

4)插值；

5)CT图像重建和金属对象补偿.

图1(B)的CT图像金属伪影校正算法主要步骤如下：

1)CT图像重建；

2)CT图像分割和投影；

3)插值；

4)CT图像重建和金属对象补偿.

图1(A)与(B)主要区别在于图1(A)起源于投影数据，而图1(B)起源于CT图像.

1.1 投影数据输入

投影数据来源于CT成像系统，是CT成像系统通过扫描投射体后得到的结果.在基于插值的CT图像金属伪影校正算法流程图中，图1(A)通过输入获取到的投影数据，得到含有金属伪影的CT图像，当CT成像系统中投影数据获取不到或者很难获取到时，直接利用含有金属伪影CT图像，如图1(B).

图1 基于插值的CT图像金属伪影校正算法流程图Figure 1 Metal artifact correction algorithm flow chart for CT image based on interpolation

1.2 CT图像重建

CT图像重建是由投影数据重建成CT图像的过程，为医学诊断提供了手段.在这个过程中，使用的方法主要包括解析法和迭代重建算法.其中迭代法又包括代数重建法(Algebraic reconstruction technique，ART)、联合迭代重建法(Simultaneous Iterative Reconstruction Technique，SIRT)和基于统计学的优化方法(Optimization Method based on Statistics，OMS)；解析法直接傅立叶重建法和波反抽影法.

迭代法重建中首先假设断层截面是由一个未知的数字矩阵组成的，然后由测量投影数据建立一组未知向量的代数方程式，通过方程组求解图像向量.迭代重建算法由于计算代价大、普适性较差，仅在少数场合应用.

相反，由于解析法具有重建速度快而且符合当代CT成像系统体系结构，因此，实际中使用较多.在解析法中，滤波反投影重建算法(Filter Back Projection，FBP)是目前常用的CT图像重建算法，在实际之中使用最多.

1.3 图像分割和重投影

图像分割是图像处理领域常用的名词之一.它的意思是将预处理后的图像根据图像处理目的将图像划分成若干个特定的、具有独特性质的区域.图像分割是图像处理的关键步骤和图像处理后续步骤的前提和基础，也是计算机视觉研究中的一个经典难题，已经成为图像理解领域关注的一个热点.由于不同图像具有自己的特点，因此，时至今日没有统一的图像分割方法. 一般来说，基于阈值法的方法是最早的图像分割方法.根据分割时获取阈值方法的不同，基于阈值法的图像分割方法又可以分为全局阈值法、局部阈值法、自动阈值法等等.除了基于阈值的图像分割方法外，图像分割方法还包括基于区域的图像分割、基于边缘信息的图像分割方法、基于形态学的图像分割方法、基于先验信息的图像分割方法、基于特定理论的图像分割方法等等.

为了实验简单起见，本文实验时使用了基于阈值的图像分割方法对采集来的CT图像进行分割.阈值分割是最常见、最简单，也最适用的图像分割算法.该算法主要根据图像像素的灰度值来确定对应的分割阈值.根据选阈值方式的不同，可以分为以下两种形式.1)如果图像目标单一，只需要选取一个确定的阈值，就可以将图像划分为目标和背景两大类，这就是单阈值分割；2)如果图像目标比较复杂，需要根据目标区域和背景区域的特点选择不同的阈值对图像进行分割，这就是多阈值图像分割.在使用阈值对图像分割过程中，最关键是如何取得一个合适的阈值.式(1)是使用阈值对图像进行分割公式：

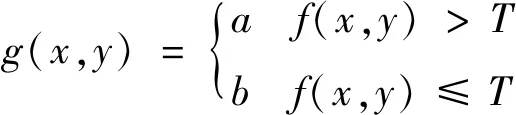
(1)

其中：T是阈值，f(x,y)是待分割的图像在坐标(x,y)处的灰度值，g(x,y)是分割后的图像灰度值.公式(1)的表示图像在(x,y)处的灰度值大于T时，分割之后图像的灰度值为a，表示图像在(x,y)处的灰度值小于等于T时，分割之后图像的灰度值为b.通常情况下，a和b分别为1和0，分别表示前景与背景.从公式(1)中可以看出，T的确定对f(x,y)分割起着关键性的作用，只有确定精确的T才能精确的把图像分割开；相反，如果T确定不好，将很难将目标图像和背景图像分割开.

1.4 插值

通过确定阈值并对图像进行分割后，原图像被分割成金属图像和非金属图像.为了消除原CT图像中的金属伪影，算法将获取到的金属图像与非金属图像进行投影，并得到对应的金属图像投影正弦图，非金属图像投影正弦图.

为了消除CT图像中的金属伪影，首先，根据金属对象投影正弦图确定其在原始CT图像投影正弦图中的位置与形状，然后使用非金属投影正弦图数据对金属对象投影正弦图中的数据进行插值并填充对应的位置.

实验过程中，为了加快算法的运行速度，这里使用了插值方式去除金属伪影.插值法有内插值法和外插值法，这里主要用了内插值法.内插值法是一种根据已经二个或以上端点坐标值，求出端点之间某点坐标及其对应值.

根据插值时所使用基的不同，又可以分为拉格朗日插值、牛顿插值、埃特肯插值、埃尔米特插值和样条插值等.这里重点介绍一下拉格朗日插值，以满足实验的需要.

拉格朗日插值问题可表述为：求作次数≤n多项式Ln(x)使满足插值条件：

Ln(x)=yi(i=0,…,n)即为拉格朗日(Lagrange)插值.

拉格朗日(Lagrange)插值公式的基本思想是：把构造插值多项式的问题转化为构造(n+1)个插值基函数li(x)(i=0,1,…,n).

为了比较次数对CT图像校正结果的影响，这里选择了拉格朗日线性插值、拉格朗日二次多项式插值和拉格朗日四次多项式插值.

1.4.1 拉格朗日线性插值[14-15]

拉格朗日线性插值的问题：已知函数y=f(x)在点x0，x1上的值为y0，y1，求作一次式，使满足条件：

L1(x0)=y0,L1(x1)=y1

(2)

如图2所示可知.由直线两点式可知，通过A，B的直线方程为，

图2 线性插值示意图Figure 2 Linear interpolation diagram

(3)

式(3)称为线性插值公式.该式又可以被写成：

L1(x)=y0l0(x)+y1l1(x)

(4)

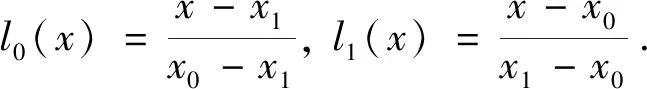
(5)

1.4.2 二次多项式插值

拉格朗日(Lagrange)二次多项式插值问题可以表述为：求作二次多项式L2(x)，使满足条件：

L2(xj)=yj(j=0,1,2)

(6)

拉格朗日二次多项式插值是拉格朗日线性插值的延伸和扩展，在几何解释是用通过三个点的抛物线来近似考察曲线.类似于拉格朗日线性插值，构造基函数，要求满足：

L2(x)=y0l0(x)+y1l1(x)+y2l2(x)

(7)

即拉格朗日二次多项式插值表达式为：

(8)

1.4.3 四次多项式插值

拉格朗日(Lagrange)四次多项式插值问题可以表述为：求作四次多项式L4(x)，使满足条件：

L4(xj)=yj(j=0,…,4)

(9)

同样地，拉格朗日四次多项式插值是拉格朗日线性插值的延伸和扩展，是拉格朗日多项式插值的特例.类似于拉格朗日线性插值，构造基函数，要求满足：

L4(x)=y0l0(x)+y1l1(x)+

y2l2(x)+y3l3(x)+y4l4(x)

(10)

即拉格朗日四次多项式插值表达式为：

(11)

1.5 CT图像重建和金属对象填补

在非金属投影正弦图中，金属对象所在区域使用插值方法获取数据并填充后(不含金属部分)，使用滤波反投影算法重建校正后的正先弦图，得校正后的图像.由于重建后的CT图像中不含有对应的金属对象补充，必须将金属对象填补到重建后的CT图像中，得到最终CT图像.

2 实验与结果分析

为了比较多项式次数对CT图像校正结果的影响，使用了临床CT图像.临床CT图像是从国外某医疗机构网站上下载.实验环境是Matlab R2012a和Win7操作系统.

实验时，参加比较的量主要是均方根差(root mean square error，RMSE)和 以及系统运行时间.其中均方根差，也称为方均根偏移是一种常用的测量数值之间差异的量度，计算公式如(12)所示：

(12)

其中：M和N分别表示图像的宽度和高度.xij是图像中第i行和第j列的灰度值.X是图像灰度值的平均值.

图3显示了理想图像、模拟图像和校正后图像，表1是其对应参数表.

表1 模拟模型参数Table 1 simulation model parameters

表2显示了模型理想图像与含有金属伪影的原始图像、线性插值校正后图像、二次多项式插值校正后图像和四次多项式插值校正图像.其中“L-MAR图像”、“Q1-MAR图像”和“Q2-MAR图像”分别表示使用线性插值校正结果、二次多项式插值校正结果和四次多项式校正结果.

表2 各种图像与参考图像之间的均方根差Table 2 Root mean square difference between various images and Reference image

从表2可以看出，原始图像的均方根差是0.4270，L-MAR图像的均方根差是0.3465，Q1-MAR图像的均方根差是0.3209，Q2-MAR图像的均方根差是0.3102.

图4表示线性插值校正法运行时间、二次多项式插值校正法运行时间和四次多项式插值校正法运行时间.

从图4可以看出，线性插值校正算法运行时间为0.297 704，二次多项式插值校正算法运行时间为0.302 814，四次多项式插值校正算法运行时间为0.325 467.

图4 线性插值、二次多项式插值和四次多项式插值运行时间Figure 4 Running time of linear interpolation,quadratic polynomial interpolation and quartic polynomial interpolation

3 结 语

放射状的金属伪影是影响CT图像质量的重要因素之一.因此，在基于CT图像的临床应用领域，在使用CT图像之前必须要进行CT图像清晰化.线性插值作为最早使用的校正方法具有简单且运行快的特点.在线性插值的基础上，人们又提出的多项式插值.通过实验，本文比较了多项式的次数对CT图像校正结果的影响.实验结果表明，一次线性插值校正方法运行速度最快、二次线性插值校正方法运行速度次之，四次线性插值校正方法运行速度最慢.均方根差(RMSE)方面，原始含有金属伪影的CT图像最大，一次线性插值校正方法次之、二次线性插值校正方法再次之，四次线性插值校正方法最小.

总而言之，在使用多项式插值校正CT图像金属伪影的过程中，随着多项式次数的增加程序运行的越来越慢，运行时间越来越长；图像质量方面，均方根差(RMSE)越来越小.