浅谈转化与划归思想解决简单数学问题

牛松涛

（鞍山市第二十四中学，辽宁鞍山 114000）

1 问题的提出1

现在高中学生在学习数学的过程中普遍存在解题思想的混乱，特别是在有关简单问题时往往找不到方法。所以探寻本质，数学学习的核心是站在思想的高度来思考和引领方向，进而解决数学问题同时提高数学学科核心素养。

2 问题的解决与思考

2.1 实例分析

角度1与圆有关的问题。

数学活动的实质就是思维的转化过程，在解题中，将未知的，陌生的，复杂的问题转化为已知的，熟悉的，简单的数学问题

例如若实数

x

，

y

满足(

x

-2)+

y

＝3.求：

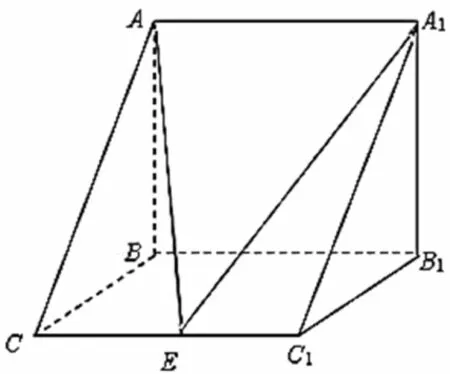
图1 三棱柱

前两问着重考察的立体几何的基本内容，第三问就不同了，如图（1）出现了一个动点，如果要是以点坐标的形式来考虑，那要需要三个未知数，但如果把动点的问题转化为定点问题，即可做到简化问题，使动点变为定点问题，解构便简便许多。

2.2 操作实践

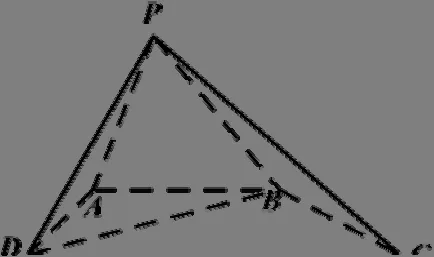
图2 三棱锥

（1）求证：平面

PBD

⊥平面

PBC

；

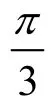
通过变式题的解答过程即通过将未知的问题转化为已知问题，找出解决未知问题的方法，从本质上看即是化归解题过程。所以，要让学生真正掌握并会应用化归思想，增加合理的变式练习。加强学生解答变式题的练习，可使学生获得更具体清晰的思路，明确化归的方向。熟练扎实地掌握基础知识基本技能和基本方法，是转化的基础。

为了实施有效的方法，既可以变更问题的条件，也可以变更问题的结论，既可以变化问题的内部结构，又可以变化问题的外部形式，既可以从代数的角度去认识问题，又可以从几何的角度去认识问题。

3 结论

最后，化归与转化的思想是中学数学解题的重要思想方法，但它并非万能的方法，化归的思想，成功应用是以数学发现为前提的，因此我们不能只停留在划归的分析，而必须有创造的精神，不断地进行新的研究，在研究中获得新方法新理论。