利用软计算技术改善圆锥滚子轴承的工作性能
卢彦群,侯建伟
(河北工程大学,河北 邯郸 057000)
1 前言
双列圆锥滚子轴承(TRBs)用于在静态和动态条件下支撑预紧力(P)、轴向载荷(Fa)、径向载荷(Fr)和扭矩(T)等 4 种载荷及其组合。该类轴承由 2 个内圈、1 个外圈和 2 组圆锥滚子组成,2 个内圈之间由一个等宽的间隙(δ)隔开,圆锥滚子在内、外圈之间形成两列。δ 的作用是便于调整轴承的整体游隙和预紧力,并便于承受 P、Fa、Fr和 T 的作用。组合式载荷会在轴承滚道上产生接触应力(S)和局部变形(α),也会引起滚道自身的旋转和 δ 的变化,这很难进行实验预测和验证,此外,如果轴承上承受的载荷与制造商的建议值不同,则轴承可能出现故障。譬如,如果 P 值较小,Fr和 T 值很高,则可能在滚道上产生超过 1 000MPa 的 S 值和显著的局部变形(αmax)。这可能会导致缺陷产生,如点蚀和疲劳剥落[1]。除了这些不希望的摩擦学问题外,P 的降低可能导致外滚道的某些接触区域产生更大的应力,进而导致滚子脱离外滚道[2]。因此,通常通过分析技术或数值方法(如有限元法——FEM)来确定此类机械装置的最佳载荷组合。虽然使用有限元法有许多明显的优势,但它的确也有一些缺点:比如在利用有限元模型处理机械接触、大位移和材料非线性问题时,会产生高昂的计算费用,且在处理机械接触问题时的一个最大缺陷是网格尺寸及模型收敛问题,也就是说,如果圆锥滚子和滚道之间的接触面较小,而两个接触体之间的单元格尺寸较大,则接触应力的计算将不太准确[3]。一些研究人员[4]采用这种方法,分析了在若干种 P 和 Fr作用情况下的接触体网格尺寸对圆锥滚子和滚道之间接触应力的影响。
众所周知,单独使用有限元(即没有软计算或数据挖掘——DM技术)来优化运转工况或预测轴承故障的设计方法,涉及到不可接受的计算成本问题。因而,为了预测安装在双列 TRB 上的轮毂的接触应力分布,洛斯塔多等人使用了基于 DM 技术的各种类型的回归模型。其应力分布由 P、Fr和摩擦系数决定,所得回归模型可作为该类机械装置设计阶段的可行方案。此外,为了优化这些机械装置的运行状况,洛斯塔多等人[5]还采用了有限元和 DM 相结合的方法,以确定双排 TRB 的最大承载能力。在这种情况下,研究的重点是找到输入载荷(P、Fa、Fr和 T)的组合方式:当两排滚子的接触应力比都接近 25% 时,Fr最大,即此时具有最大承载能力。其他一些研究者使用基于机器学习法的分类技术来事先预测轴承的失效与故障,这些预测滚子大多数仅仅依赖于实验数据。例如,为了预测滚动轴承的失效,苏古曼等人采用了决策树以及基于内核的邻域得分和多类支持向量机(SVM)等手段,其中涵盖了状态良好的轴承、内圈故障的轴承、有外圈故障的轴承和有内外圈同时存在故障的轴承。格里亚斯和安东尼亚迪斯[6]使用 SVM 方法对滚动轴承故障进行自动诊断,这是一种有效的方法,在滚动轴承故障诊断中具有潜在的应用价值。最近,康卡等人采用人工神经网络(ANN)和 SVW 检测和诊断滚珠轴承的机械故障,通过对各种缺陷的振动响应分析,对神经网络和支持向量机进行训练和测试,结果表明,上述算法可用于轴承故障的自动诊断。蒋川等人提出了一种新颖的、基于经验的小波变换和模糊相关分类的滚动轴承故障诊断新方法,实验表明,该方法能有效地诊断滚动轴承的三种不同工作状态,且检测率高于 SVW 和反向传播神经网络(BPANN)。
新近出版的文献采用基于 FEM 和 DM 相结合的分类技术,来探究 TRB 的最佳运行条件。用于对定义承载条件的明确响应进行分类的 DM 技术可分为有监督数据集和无监督数据集[7]。在有监督数据集中,每个数据实例的类标签是已知的,新实例由构建模型进行预测;然而,在无监督数据集中,没有实例标签,且可以用一组特定的相似度量对实例进行分组。有监督数据集和无监督数据集技术都有应用,但鉴于无监督技术的结果不能令人满意,故在该项工作中对有监督技术给与了更多的关注。无监督分类算法是基于有限正态混合模型的一种聚类算法,而有监督分类算法数量较多,本文将其分为以下几种:线性分类法、非线性分类法、分类树和基于规则的分类法。
本文的主要目标是建立精确的模型,以更高的精度自动区分双列 TRB 的预设运行状态——从几个预先配置的 P、Fa、Fr和 T 负载组合来定义该状态(例如:坏、差、好和优)。分类模型可以提供运行状况的相关信息,包括某些不良状况的附加信息,比如过高的接触应力、过大的局部变形、点蚀和疲劳剥落等。为了实现这一目标,将机器学习法应用于从双排 TRB 的有限元模型中所得的数据集,这些若干负载下的数据集可以定义实验设计(DoE)后的运行状况。而后,创建了几个模型并对其特征进行约减、数学变换和参数整定,接下来,根据几个鲁棒性标准对所选模型进行测试,以确定其泛化程度[8]。
2 材料与方法
2.1 双列圆锥滚子轴承的负载组合与滚子条件
图1a 显示了施加在每个 TRB 部件上载荷状况(P、Fa、Fr和 T):内滚道上施加 P 荷载,外滚道上施加 Fa、Fr和 T 荷载。内圈被 δ 分隔成两边对等的滚道,以便于轴承的拆卸和 P 的施加。由此可以理解,影响 TRB 的载荷是怎样组合而成的,轴承是否可能会出现故障。例如,如果 TRB 上的组合载荷值等于制造商的建议值,则 δtop应等于 δbottom(见图 1a),此时,外滚道的顶部和底部区域的接触应力值不等于零(见图1b),在这种情况下,所有滚子始终与内外滚道保持机械接触,而且局部变形量与接触应力也较小,这样可以避免出现疲劳剥落和点蚀。与此相比,如果轴承承受不恰当的载荷(例如:过高的 Fr和 T 值,再加上较低的 P 值),那么 δtop与 δbottom则会不同,其结果会导致的 TRB 故障运行(见图1c)。如图 1d 所示,只有一小部分外滚道(上部区域)承受非常高的应力,而外滚道底部区域的接触应力值则为零。这将导致出现点蚀和疲劳剥落,进而导致 TRB 故障。为了量化具有两列滚道轴承滚子的“悬起”效应,对 TRB 的每列滚子的接触比 S 做如下定义:

图 1 所研究轴承的主要组成与负载
式中,Stop为各列滚子的顶部接触应力,Sbottom为各列滚子的底部接触应力。如果两列滚子的接触比(S1和 S2)大于 20%,则可防止 TRB 滚子悬起。
此外,为了量化轴承滚道的旋转效应,从而判断轴承故障,将间隙差(Δδ)做如下定义:

式中,δtop为 TRB 顶部内圈间隙;δbottom为 TRB 底部内圈间隙。TRB 正确运行的最佳条件是其Δδ 已尽可能减小。
但是,为了尽量减少外滚道的正常局部变形,以避免出现点蚀或疲劳剥落,在埃诗曼等人研究成果的基础上,提出下式:

式中,αmax为最大局部变形量;dr为圆锥滚子的平均直径(此处,其值等于 11.3 mm)。所以,作为一般规则,本案例中的 αmax的值在任何点都不应超过外滚道 0.001 13mm。
一旦确定了 TRB 能够正常工作的条件,就要考虑各工况下 δ、α、S1和 S2的取值范围。本文将工况分为四类(坏、差、好和优),每类工况示踪的实例数如下:“坏”工况,试验 15 例,检测 4 例;“差”工况,试验 16 例,检测 14 例;“好”工况,试验 27 例,检测 6 例;“优”工况,试验 25 例,检测 6 例。表 1 根据检测结果概括了各工况下的参数范围。

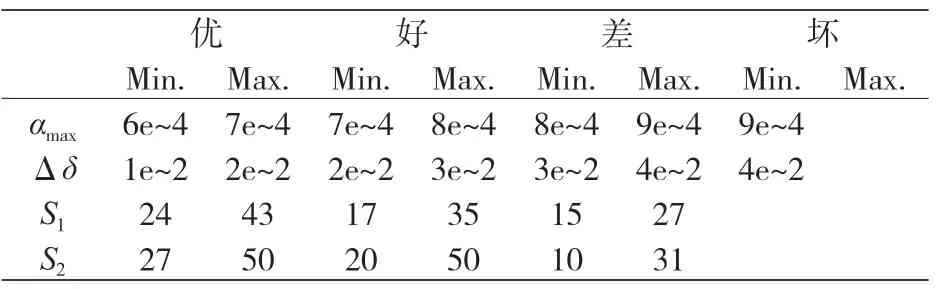
表1 各类工况下的参数取值范围
2.2 双排 TRB 的建模与实验验证
在本案例中,为研究不同载荷组合,建立了的轴承三维有限元模型(其中包括圆锥滚子、内外滚道及用来安装 TRB 的轮轴),并利用一个双列 TRB 的一半模型进行了模拟。为了降低仿真计算成本,本案例仅考虑对称几何条件和对称加载状况,且将 8 节点和 6 节点的三维有限元结合起来,并使用线性函数进行完全积分,从而构建 TRB 有限元模型。该研究所涉及的 TRB的几何尺寸为:孔径 78mm,外径 130mm,宽度90mm,每列 25 个圆锥滚子。根据经验并结合实际情况,假设轮轴和内圈之间的摩擦系数为0.2,滚子与内圈之间以及滚子与外圈之间的摩擦系数为 0.001。完整的 TRB 有限元模型由 734 84个单元、84 009 个节点和 3 289 个自由度组成。与传统的“节点-段”接触检测算法相比,“部分分隔”接触检测算法能够减少计算接触应力的误差,同时可以减少接触应力的网格密度[9],为了改善 TRB 不同部分之间的机械接触检测质量,本研究选择了后者。整个有限元模型的雅可比因子始终大于 0.6,因此,没有生成零体积的元素,此外,任何元素的纵横比(定义为元素最长边缘与其最短边缘之间的比率)从未超过10:1。
在材料属性上,赋予圆锥滚子与滚道以线弹性和各向异性钢,且滚子的杨氏模量(E)为 208GPa,泊松比(ν)为 0.29。轮毂是以E = 200GPa 和 ν = 0.29 的假设而建模。TRB 的不同组成部分如图 2a 所示,调整后的有限元模型最终网格尺寸如图 2b 所示。

图 2 三维有限元模型
该案例对所提出的有限元模型进行了调整和实验验证,使所得结果尽可能真实。这一过程通过对接触运动副(滚子和滚道)的网格尺寸以及滚道之间的相对位移的调整来实现,其中施加的力 P 分别为 300、400、500 和 600 N,力 Fr为 2 000N。
2.2.1 滚子与滚道网格尺寸的匹配
众所周知,机械接触问题中的非线性是有限元法求解实际接触应力的主要难点之一。就这类非线性问题而言,有些有限元模型只具有有限的接触面,而网格尺寸很大,这很可能产生不切实际的接触应力。这一问题往往通过使接触副之间的网格更小化来解决,即增加接触节点的数量,或增加有限元模型函数的多项式次数[10]。为此,德米汉和坎伯对圆柱滚子轴承的有限元模型进行了调整。该案例研究了单元格大小对滚道与滚子接触应力的影响以及内外滚道的相对位移等情况,同时还对滚子和滚道之间不同网格尺寸的接触应力与理论数据进行了比较,其间,当有限元模型所得结果与理论和实验所得结果之间的差异不显著时,模型调整完成。类似于德米汉的工作方式,本案例逐渐递减网格尺寸,相继构建出含局部精细网格接触区域的有限元模型。这种通过使用渐小化网格尺寸来创建连续网格的方法需经过不断改进,直到这些有限元模型外滚道上的接触应力与理论模型上的接触应力几乎没有差异为止。本案例以赫兹[11]圆柱体理论模型为基础,对所提出的有限元模型的不同网格尺寸进行了比较,并使用平均绝对百分比误差(MAPE)来确定有限元模型的网格大小何时有效。MAPE 的定义如下:
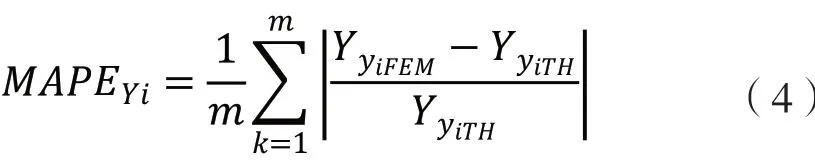
式中,YyiFEM为每个有限元模型在不同拟用网格尺寸时的接触应力;
YyiFEM为理论模型中的接触应力;m 为各尺寸网格下的节点总数;
k 为局部接触区各节点的接触应力之一;
yi 是调整参数,在本案例中对应于接触面积元素的网格大小。当接触元素(包括滚子和滚道)接触区尺寸分别为 5.1、1.0 和 0.2 mm时,网格尺寸调整所获得的 MAPE 如表 2 所示,它显示了预加载 P 分别等于 300、400、500 和 600 N 和
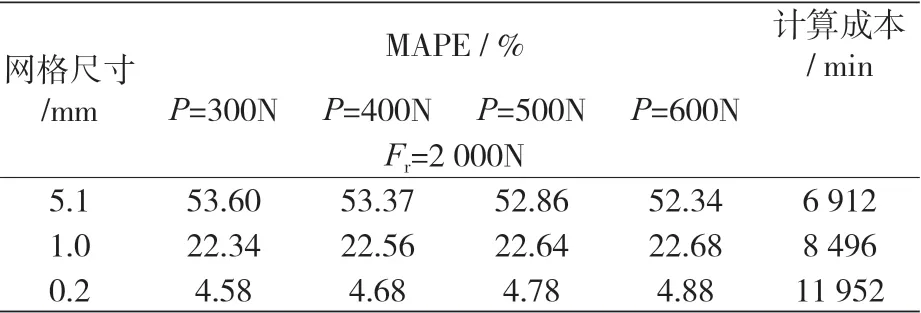
表2 调整网格密度时,有限元模型的MAPE及其计算成本
Fr等于 2 000 N 时的 MAPE,此外还对每个网格所需的平均计算时间进行了探讨。
根据经验,当 MAPE 小于 6% 时,才被认为是合理的,当然还要考虑计算成本,因为对任何使用 FEM 解决的问题,其 MAPE 和计算成本都要达到预期的目标,以此为准则,本案例中满足此要求的要素是那些网格尺寸为 0.2 mm 的单元格(对所有的 P 进行预加载和模拟,其 MAPE 和计算成本均低于阈值)。
2.2.2 基于滚道相对位移的 TRB 的调整
在有限元模型的验证中,但凡对网格尺寸做出调整,都要考虑内外滚道的相对位移的变化,因为内外滚道的相对位移主要用于检验有限元模型的网格尺寸、摩擦系数和弹性特征(E 和 v)的是否恰当。实验中,用图 3a 中所示的、带有 2 只红色铅笔的比较仪来测量该相对位移,在有限元模型中,该位移在属于模型本身对称平面的两个节点之间进行测量,如图 2a 所示。在网格尺寸调整过程中,载荷 P 值分别为 300、400、500 和 600 N,Fr值为 2 000 N。Fr通过加载单元(型号为 HBM U3,加载能力为 5kN)施加于 TRB,P 由一个螺丝通过一个钢质套管施加在轴承内圈上,用一个安装在套管上的应变仪来测量 P 值,在拧动螺丝时,套管压向内圈。图 3b 显示了不同 P 值和 Fr值下,从试验台获得的相对位移与从有限元模型获得的相对位移之间的差异:虚线表示实验产生的相对位移,实线表示有限元模型产生的相对位移。这些成对儿的曲线表明,所获得的这两种相对位移之间的差异较小,此外,图 3b 也表明,无论是有限元模型还是实验数据,当施加最低的 P 时,相对位移较大,当施加最高的P时,相对位移最小,同时图 3b 还表明,随着预紧力的增加,滚道与滚子接触刚度增加,TRB 变形减小。图 3c 表达了通过实验和有限元模型得出的不同相对位移值的详情,这种刚度变化与考兹拉丝和卡尼亚[12]之前报道的荷载-挠度关系非常吻合,这表明 TRB 中的预载值越高,其刚度越大。从图 3b 还可以推断出:如果网格尺寸有效,那么与实验数据和有限元模型的预设参数(Ebearing= 200 Gpa,Ehub= 208 GPa,ν = 0.29,摩擦系数 = 0.001 和 0.2)相一致。虽然优化过程中使用的荷载比网格调整过程中使用的荷载高(见表 4),但在 2.2.1的预设参数和网格尺寸描述中,已经为优化过程中的所有有限元模拟做了设置。这主要是因为在优化过程中 TRB 所承受的载荷始终在厂家规定的范围内,所以,TRB 的所有部件都不会发生永久性变形。
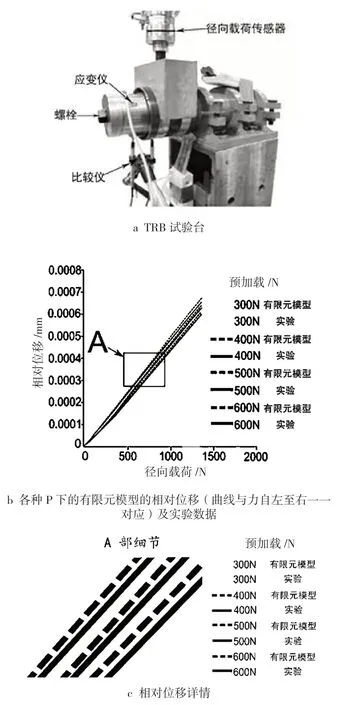
图 3 内外圈相对位移监测
2.3 实验设计
因为需要考虑的变量和因子的数量及每个变量的级差非常多,所以,所取样本数无法覆盖整个可能性空间,因此,实验设计在这项工作中的应用,大大减少了取样组合,在模型所需的样本数量和有限元模拟实际需求之间,提供了一个很好的折衷。本案例实施了 3 个层级的 3k 全因子DoE,其层级与因子数值见表 3。
在建立了如表 3 所示的因子和层级后,生成了设计矩阵和荷载组合。该案例必需要进行 81次实验或有限元模拟,以尽量涵盖所有可能性,并随之优化预设负载,以改善双排 TRB 的工作条件。表 4 给出了所实施实验或有限元模拟的次数,以及要模拟的负载值。

表3 基于各因子和3K全因子法的DOE参数、范围、等级选择

表4 设计矩阵及拟模拟的载荷组合
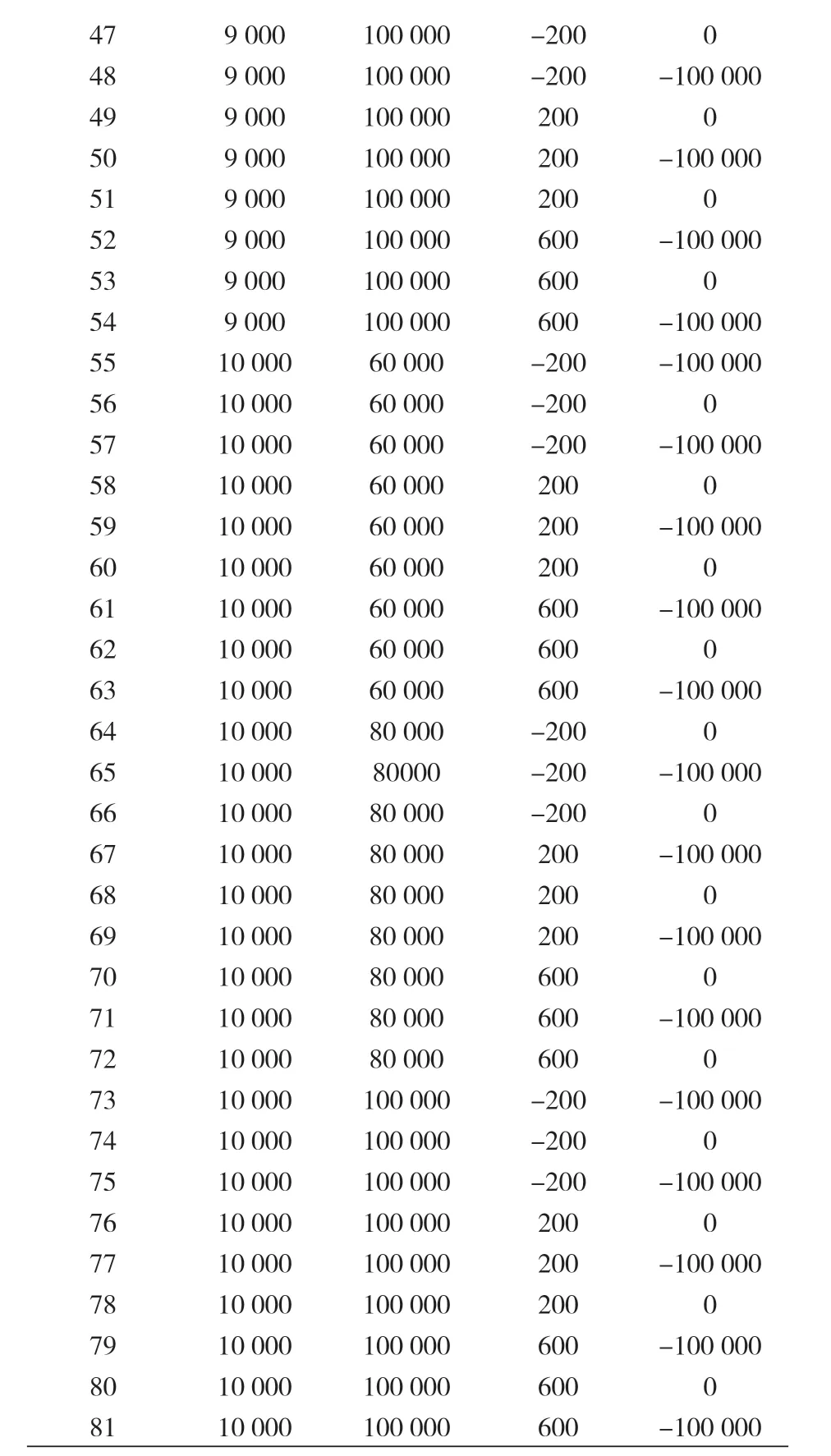
?
2.4 数据的多变量与聚类分析
为了平衡变量的权重并改善统计分析结果,首先,在使用分类方法之前,对所有数据集中的变量,都在 0 和 1 之间进行了规范化处理,然后,对差异性和相关性进行了探索性分析,对方差进行了统计分析。方差统计涵盖参数性分析和非参数性分析,包括方差分析、巴特利特检、布朗-福赛斯分析以及弗莱格-凯琳检测[13]等。这些分析旨在确定每个特征的意义,确定这四类方法之间是否存在显著差异,是否包含任何冗余特性,此外,主成分分析(PCA)生成了一个具有新特征的新的数据集,并在随后对其进行了研究。差异和相关性分析是一种流行的方法,成功地运用于该课题[14],它产生变量初始空间的正交变化,以创建一组称为主成分(PCs)的变量。正交投影捕捉数据中的大部分方差,并将一组相关成分转换成一组非线性相关的成分。此外,为了最终应用所提出的分类方法,对所提出的DoE中的数据进行了聚类分析,以确定输入变量是否能够便捷地定义分类问题。
2.5 监督分类法
该课题采用了几种监督分类技术,按照所研究的四个类别对双排 TRB 的呈现条件进行分类。

表5 采用的分类技术
为完成这一过程,将包含选定特征的数据集用作输入,而这些特征定义了预设条件(P、Fa、Fr和 T)。为了简化模型,建立了鲁棒性更好的分类模型,对其进行了特征约简和参数调整,而后,对这一阶段的模型进行了测试,以确定它们的实际推广能力,此外还对模型的性能测试结果进行了比较,以确定和选择最准确的模型,最后,对结果进行验证,以确保模型能够在不经过量训练的情况下,尽量解决更多问题。
整个分类过程按照以下方法进行:把数据集分成 2 组——第 1 组叫做训练数据集,由计划 DoE 的 81 个样本组成;第 2 组叫做实验数据集,由在 DoE 中所建议范围内的一些随机实例所形成(32 个样本)。选择训练数据集并使用重复 10 次的交叉验证来构建和培训模型。由于某些方法(例如,神经网络或支持向量机)在学习过程中使用随机初始值,因此该培训有必要多次重复(本案例重复了 50 次),以提高结果的准确性。在培训过程中,设法调整每种算法的最重要的参数,以获得更好的结果,对于每种算法,选择最精确的模型进行测试,而且在此期间使用了尚未用于培训的数据集。这种测试可以选择最精确的模型,因为它们的精确性是通过以前未使用的实例来确定的。对于每种分类技术,在选择了最精确的模型后,对该选择过程进行了验证,结果表明,所选模型能够成功地解决各个方面的问题,最后,根据这些最精确的模型,对最优预设值进行了最佳分类,确保了 TRB 的正确的工作条件。
2.6 鲁棒性准则
模型的鲁棒性是模型选择中一个实用的参数,而其作为一个目标函数,通常情况下需要通过 95% 置信水平下的整体分类来验证其精度。当总体分类准确度相似(比如:灵敏性、非加权卡巴统计、特异性、检出率、发病率、阳性预测值、阴性检出率、预测值和平衡精准度等)时,也考虑其他标准(见表 6)。

表6 优化分类模型准确性且可以选择最佳分类模型指标
在 v3.4.1 统计软件环境下,用 R 语言对提议的方法进行编程,并开发分类模型[15]。
3 结果与讨论
3.1 FE 模型结果
一旦 FE 模型通过验证,自动程序则会根据表 4 中所建议的 DoE 进行 81 次有限元模拟,其结果如表 7 所示(S1、S2、αmax和Δδ)。

表7 基于表4定义的DoE的81次有限元模拟结果
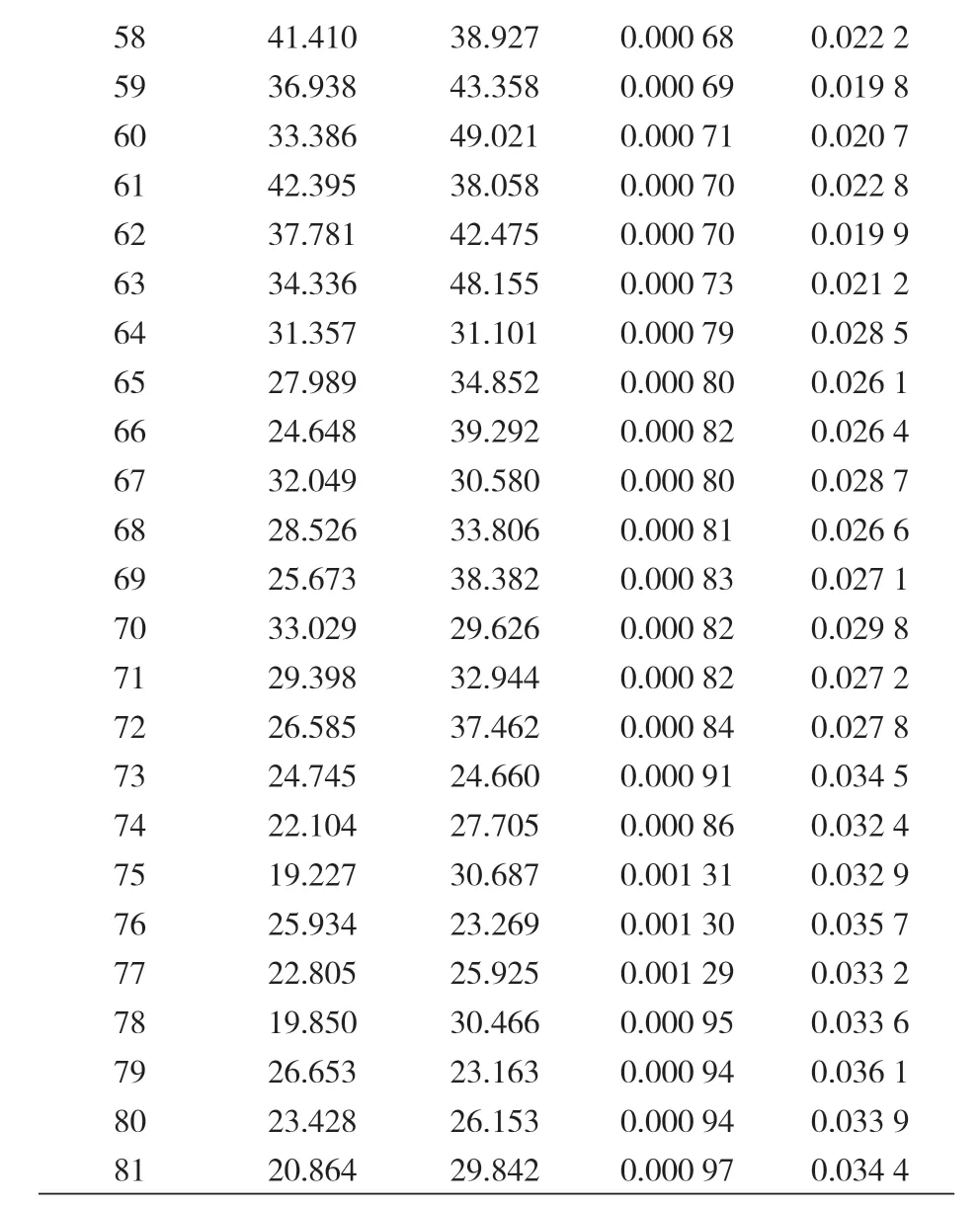
?
图 4 表达了根据施加荷载(见表 1)情况和从有限元模拟(见表 7)结果中获得的数据集分布,其中图 4a 显示了αmax、S1和 S2的三维图形数据集分布,图 4 b 显示了Δδ,S1和 S2的三维图形数据集分布。在这两个图中,都可以看到与优、好、差和坏条件相关的图案结构。
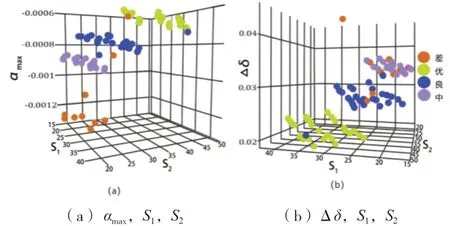
图 4 载荷与模拟数据集分布
此外,32 个新的有限元模型被用于新的荷载组合测试分类程序(见表 8),同样,用一个自动程序来运行 32 个新的有限元模拟,其结果见表 9。

表8 新荷载组合模拟

表9 按表8输入的有FE模拟结果

?

?
3.2 多元分析与无监督分类
实验进行期间,按照提议四种方法的对数据集的四个变量进行了方差同质性的统计检验,表 10 所列的统计数据以及 P 值均为计算值。此外,还进行了相关分析,其结论是:尽管 Fr是最重要的特征,但在当前的实验条件下,四个特征都具有重要意义。
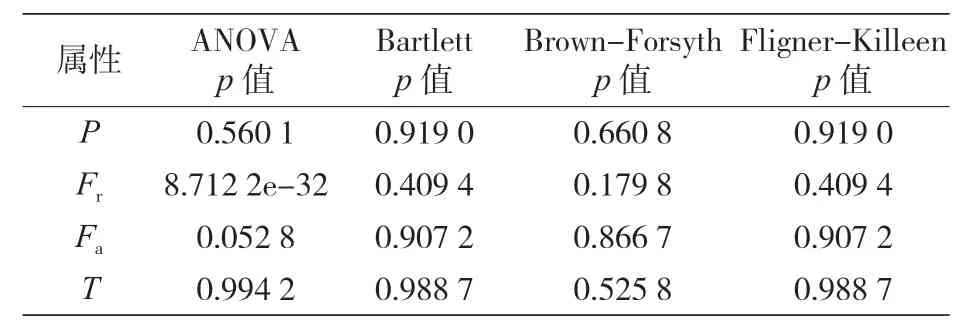
表10 各变量方差均匀性检验结果
随后,将数据集引入 PCA 中,结果表明,所有新的 PCs 所阐释的数据方差比例(见表 11)与原始特征大致相同。鉴于此,人们认为使用原始特性是更好的选择,因为使用已知属性而不是它们的线性组合将构建更容易理解的模型。
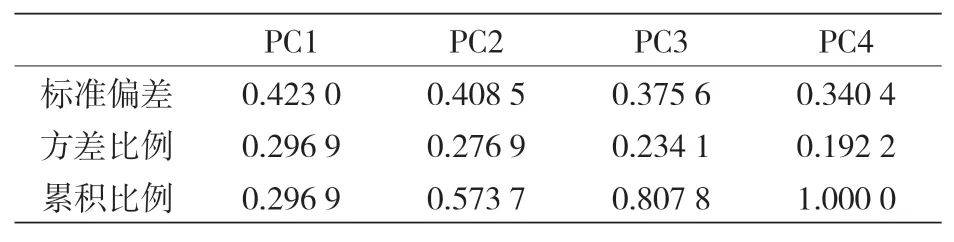
表11 PCs的重要性
从这一点出发,采用无监督聚类方法,根据 4 个原始特征得到 4 组分类。依据 DoE 信息和实例的相似性度量,使用 EM 算法拟合而成高斯有限元混合模型,确定数据的累加是否可以定义和如何定义 4 个集群。对这种无监督算法进行多元混合评价(见图 5),可以看到,贝叶斯信息准则(BIC)在绝对值上随着集群数量的增加而显著增加。进一步的分析结果表明,采用简单的聚类技术,不能将数据按照误差较小的类划分为 4 组。对于一个集群和接下来的 3 个多元混合物(EII、VII、EEI)来说,最好的 BIC 值为343.45。
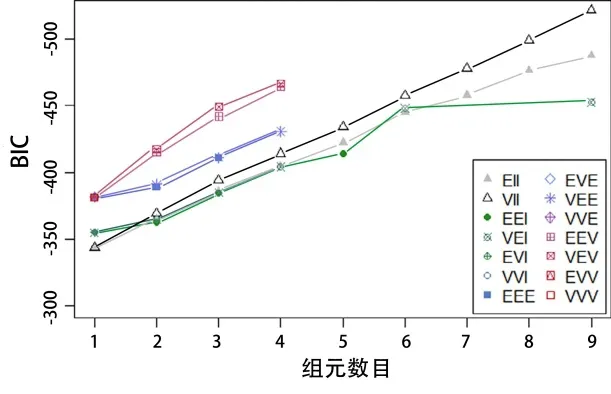
图 5 集群数与BIC的关系
多元混合体如下:EII(球形、等体积)、VII(球形、等体积)、EEI(对角线、等体积、等形状)、VEI(对角线、变体积、等形状)、EVI(对角线、等体积、变形状)、VVI(对角线、变体积、变形状)、EEE(椭圆体、等体积、等形状、同方向)、EVE(椭圆体、等体积、同方向)、VEE椭圆体、等形状、同方向)、VVE(椭圆体、同方向)、EEV(椭圆体、等体积、等形状)、VEV(椭圆体、等形状)、EVV(椭圆体、等体积)和VVV(椭圆体、变体积、变形状、变方向)。
3.3 分类技术结果
至此,由于采用 PCA 对变量进行特征约简,以及使用聚类技术对群组进行分类都没有使分类方法得到改善,因此对所有原始特征进行了监督分类,并利用该方法建立了多个模型,而且利用训练数据集进行了训练,同时,在此阶段对算法的定义参数进行了优化,提高了算法的精度。表 12 显示了技术方法、在分析期间已调优的参数、参数的调优范围以及为最终模型的选用值。一个重复 50 次的十倍交叉验证过程决定了模型的分类精度,而分析该精度的主要准则为总体精度。但是,如果对误差百分比有任何疑问,则也要对其他鲁棒性准则进行审视。

表12 各项技术最重要参数的调整及研究值的选定

?
对每种技术而言,在其最精确模型的训练阶段,都要进行测试,而测试数据集可用来确定每一种方法的实际泛化能力,培训和测试阶段的结果见表 13。这些测试表明,非线性分类方法中的 ANN 和 SVM、分类树中的 C4.5 和 evTree 以及基于规则的方法等方法在训练阶段都能得到非常准确的结果。然而,当将新的实例应用于模型时,精度要低得多。这一现象说明,在训练阶段,一些模型存在过度拟合,所以测试数据集对分析模型的真实泛化能力非常有用。
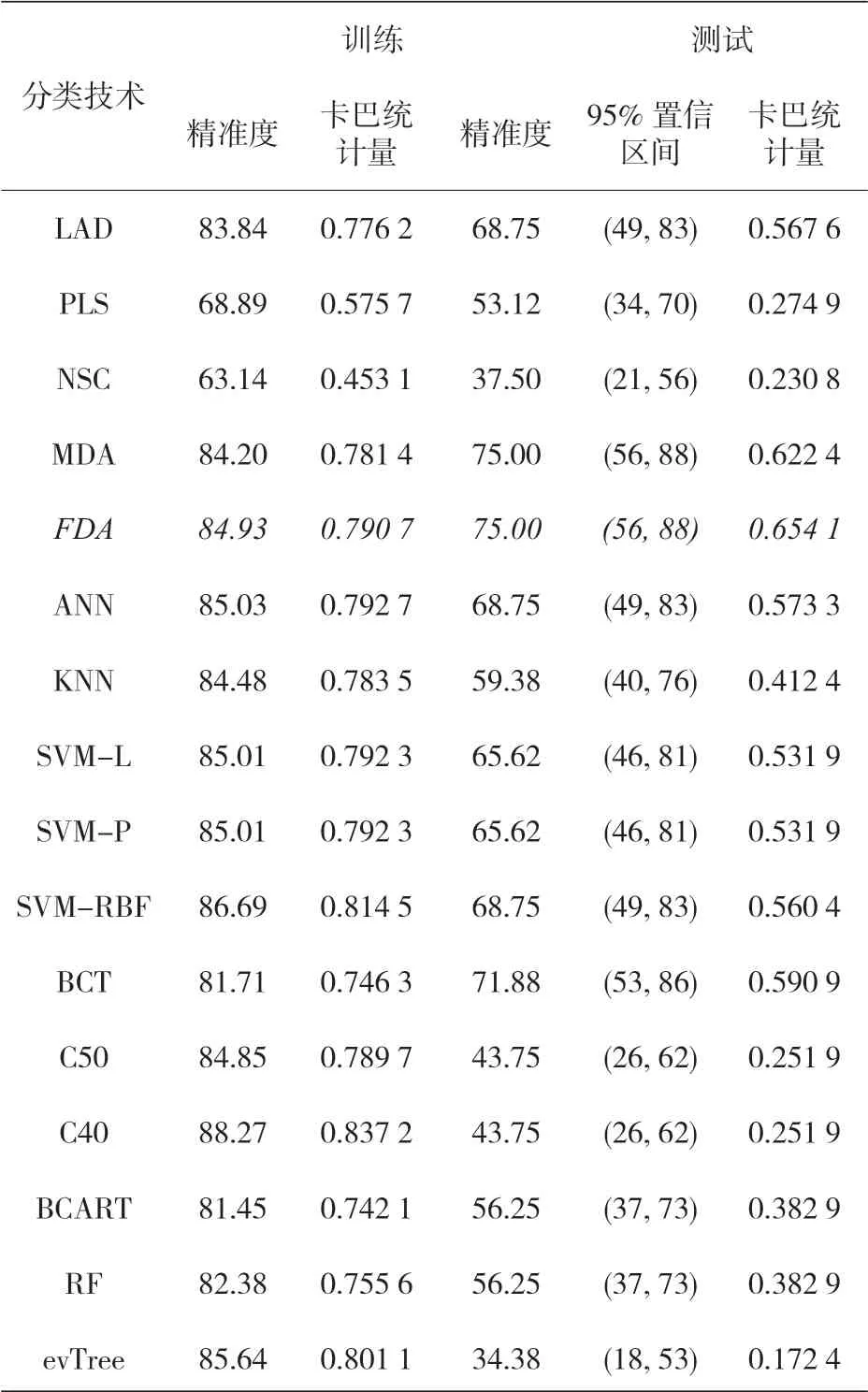
表13 使用所有数据集时,训练和测试阶段的结果(最精确的模型由斜体字表示)
这一具有所有的原始特征并基于 FDA 的模型,在对最佳预设条件进行分类的过程中,提供了最大的准确性,且基于判别分析的不同非线性技术的精度差异也不太显著,此外,为确定哪个FDA 是最准确,我们可以采用其他建议的标准来判别(例如,对于未加权的 kappa 统计,使用FDA 的价值大于使用 MDA)。
表 14 显示了使用所选 FDA 模型的测试数据集的混合矩阵,该矩阵表明,“优秀”级别的预测是相当准确的,该级别必须确保 TRB 的正确工作条件。这个预测显示出每一个被标记为“优秀”的级别是如何被预测为“优秀”的。然而,由于 16 个实例中有 6 个预测错误,所以级别被标记为“差”的实例较难分类,而“坏”和“好”级预测了所有标记的实例,只有一个例外。此外,表 15 显示了分类模型性能的更多统计信息。
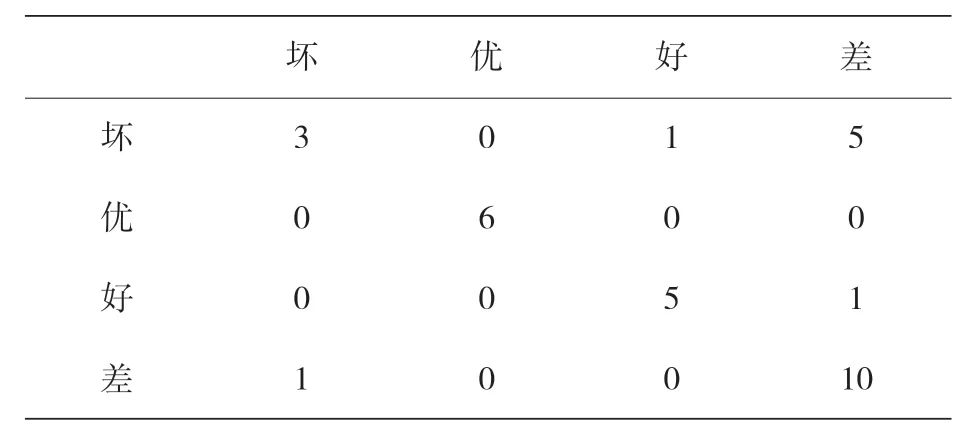
表14 基于FDA的模型在测试阶段的混淆矩阵

表15 测试阶段基于FDA的模型统计
虽然在 FDA 模型中使用测试数据集时总准确率为 75%,但当对这些结果进行分析时,可以看出该准确度可以得到提高。本案例中,可以把所定义的 4 种级别的问题简化为 2 类,第一类涵盖原来的“坏”和“差”,它使得 TRB 在不恰当的条件下运行;另一类包括了“优”和“好”,意味着 TRB 在合适的条件下工作。在本例中,表16 中显示的混淆矩阵表明,只有两个实例被预测为与其标签不同的类。这意味着当合并相关类以减少类的数量时,模型的总精度可以提高到 93.75%。

表16 测试阶段仅为“坏-差”和“好-优”两各级别的基于FDA模型的混淆矩阵
FDA 是基于 LDA 的线性技术,但有一个额外的惩罚策略,该惩罚模型采用弹性网络技术:L1惩罚实际上消除了预测因子,而 L2惩罚降低了判别函数的系数。判别空间构造模型的维数等于 3(θ1,θ2,θ3),解释模型的方差百分比在各个维度上分别为 66%、29.46%、4.54%,此外,得到的三向维度与原始特征的关系如表 17 所示,它表明在四个原始特征中,只使用了 P、Fr和Fa,没有使用 T,其中,h(·)为铰链函数,如式(5)所示。表 18 给出了用于判别空间各维度的预测结果。

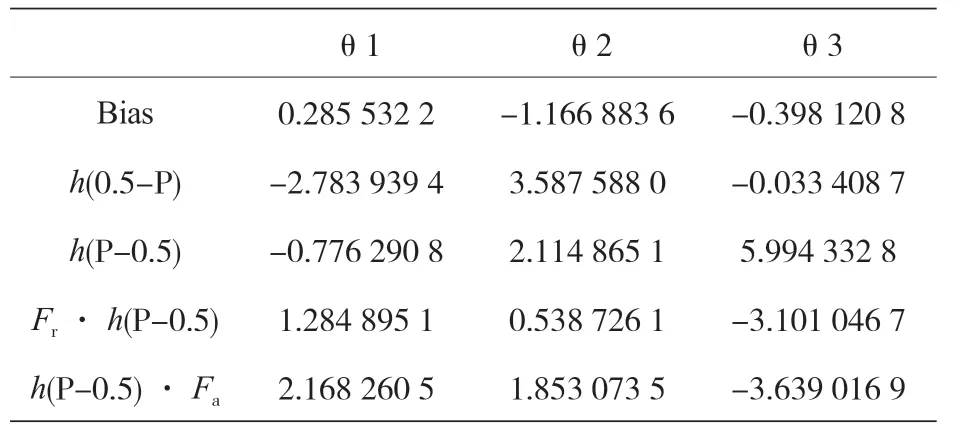
表17 所得3D模型与原始特征的关系

表18 各维和全维度的预测结果
4 结论
本文验证了一种基于数据分析和机器学习技术的两步方法,该方法既可应用于有限元模型分析,也可应用于数据挖掘。其目标是创建一个可以自动分类的组合载荷模型,该载荷可以界定一个双排 TRB 的、与其稳定的工作状态相关的预置条件。为此,建立了双排 TRB 的三维有限元模型,并成功地对其进行了数值模拟,且模拟和实验结果一致。在此模型的基础上,按照所提出的DoE方法,执行了一个将负载与定义工作条件的类别相结合的数据集,随后对数据进行统计分析,其中包括探索性分析以及方差和相关性分析,以消除不重要的变量,同时建立了几种分类模型,并通过特征约简和参数调优技术对它们进行了优化。为了确定方法的性能,使用了新的实例测试和验证了优化的模型,结果表明,一些方法在定义可能性空间时产生了过度拟合,但在生成模型时所使用新的实例没有降低模型的性能。最后,可以看出最精确的模型是在非线性分类方法组内,更具体地说,它是在柔性的判别分析的基础上产生了 93.75% 的、非常准确的结果,而最初的四个类被减少到只有两个。结果表明,将有限元法与机器学习技术相结合,可以成功地确定机械装置的工作状态。

