脉冲噪声下MSK信号解调算法研究*

齐思航 徐争光

（华中科技大学电子信息与通信学院 武汉 430074）

1 引言

在透地通信、水下通信以及大气通信中由于高频电磁波在传输中衰减很快，因此多采用甚低频段的电磁波。在常用的数字信号调制方式中，频移键控调制方式因其抗噪性能好且不易受外界环境的干扰等特点成为甚低频通信中常用的调制方式［1］，其中最小频移键控（MSK）信号作为FSK的特例，因其相位连续、包络恒定、严格正交等优势成为甚低频通信中常用的调制方式。

在传统的高斯白噪声系统下，常用的MSK信号解调算法有MSK正交相干解调以及MSK最大似然解调等［2～3］，但是在Alpha稳定噪声下，直接使用常规解调算法的解调性能很差［4］，因此需要根据脉冲噪声的分布特性对这两种解调算法进行改进，以适应Alpha稳定分布噪声下的解调方法。对于MSK正交相干解调的改进主要在于对脉冲噪声的限幅处理［5～6］；对于MSK最大似然解调［7］，有学者根据Myriad滤波思想对分支度量的表达式进行改进［8～10］。

常用高斯白噪声分布模型并不适合于描述脉冲噪声，而Alpha稳定分布因其具有统计分布的稳定性和概率密度函数的代数拖尾特点成为一种广泛使用的描述脉冲噪声的模型。Alpha稳定分布有四个参数，分别为特征指数(α∈(0，2])，它决定噪声的脉冲性强度，当α=2时，Alpha稳定分布退化为高斯分布；偏斜指数(β∈[-1，1])，它决定Alpha稳定噪声分别的偏斜程度；尺度参数(γ∈(0，+∞))，它决定稳定分布随机变量偏离其均值或者中值的程度；位置参数(δ∈(-∞，+∞))，它指脉冲中心所在的位置［11］。据此特性产生随机变量n服从Alpha稳定分布并记为n～S(α，β，γ，δ)［12］。

2 积分限幅的MSK正交相干解调

MSK信号正交相干解调法［3］是利用MSK信号的正交性将信号分成同相与正交两个部分进行处理，在同相支路中r(t)与cos(πt/ 2TB)cos(ωct)相乘，在正交支路中r(t)与-sin(πt/ 2TB)sin(ωct)相乘，然后分别在2TB内进行积分，两条支路在不同的时刻进行判决，判决后的数据经过并串转换后通过码反变换器就可以恢复最终解调数据，从接收信号进入到并串转换输出部分称为MSK正交相干解调单元，即为图1中虚线框所示部分，具体流程如图1所示。

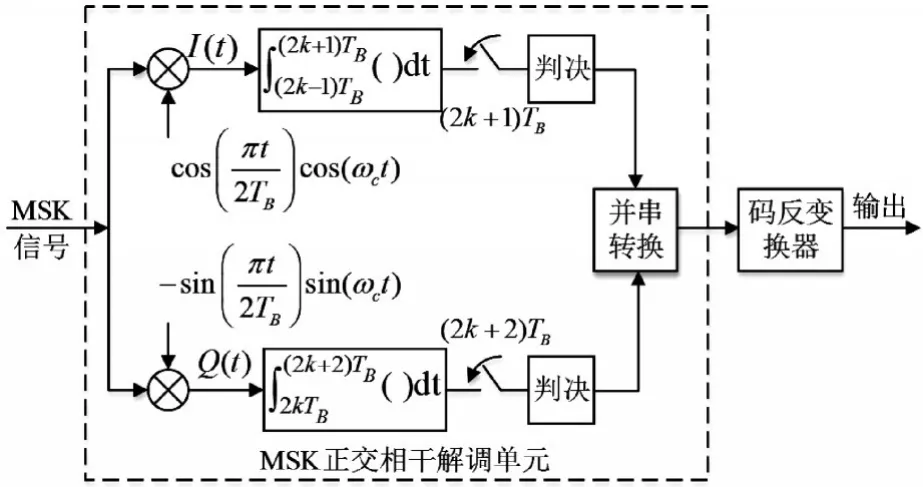
图1 MSK信号正交相干解调框图

码反变换器在判决后会带来误码率的增加，为了消除码反变换器的影响，本文考虑将码反变换器前移到进行MSK信号调制之前［4］，即作如图2所示的变化。

图2 码变换器前移到MSK调制前

若码反变换器在正交相干解调单元的后面，只有当码反变换器的两个相邻输入码元中有且只有一个码元出错时，其输出码元才会出错。假设MSK正交相干解调单元的误码率为Pe，则两个码元中前一个码元出错后一个码元正确的概率为Pe(1-Pe)，同样地，前一个码元正确后一个码元出错的概率也为Pe(1-Pe)，所以最终解调输出码元的错误概率为

当Pe很小时，有；当Pe很大时，有。由此可知：码反变换器会使误码率增加1～2倍，所以将码变换器置前的MSK正交相干解调误码率比码反变换器置后降低了1～2倍。

因为噪声信号具有很强的脉冲性，如果直接使用图1所示步骤进行正交相干解调，在脉冲点处的信号积分值会急剧上升导致判决错误、误码率上升，因此需要对脉冲噪声进行抑制。最直接简单的方法就是利用置零限幅法对含脉冲噪声的MSK信号进行限幅去除脉冲性，即对超过规定阈值的信号置零［5］，表达式如下：

其中D为阈值。这种方法虽然有效抑制了脉冲噪声，但是有用信号同时也被置零了，会带来非线性失真，同时解调性能的优劣完全由阈值的大小决定，因此本文对该限幅方法进行改进。改进之处主要体现在两点，首先不是对接收信号在进行解调前进行预处理，而是在正交相干解调单元中的积分部分进行限幅；其次在限幅阈值的确定上引入了相对阈值。下面具体来介绍实施方案。

在当同相正交的两条支路分别在2TB区间内积分时，将积分区间内所有样点的数值从小到大进行排序，将最大与最小值中各去除一定比例的数据（假设比例值为c），然后对剩余数据求取平均值即为积分单元的输出结果，紧接着按同样的判决规则进行判决。

下面以同相支路为例进行分析，接收端接收到的MSK信号经过乘法器后得到I(t)。因为接收到的MSK信号是一个模拟信号，先将其转换成数字信号进行处理。采样频率为fs，码元时间为TB，传输的码元长度为L，因此可以得到接收信号的总样点数为L×TB×fs，则一个码元时间TB内的样点数为TB×fs。由图1可知I(t)要在区间[(2k-1)TB，(2k+1)TB]内进行积分，则在此区间内样点数为 2TB×fs，即

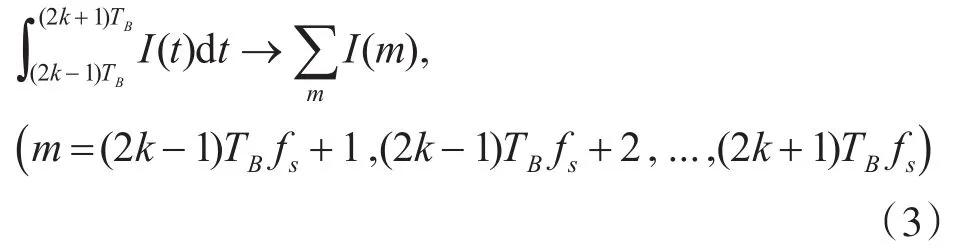
式（3）将连续函数在2TB区间内的积分转换成离散函数的累加和的形式。因为受到脉冲噪声的影响，函数I(m)中有些样点的幅值过大，需要予以舍弃。将I(m)按大小进行排序后，分别去除其中最大值与最小值的样点数为d=2TBfs×c%，即

其中，函数SMALL(I(m)，d)表示将I(m)中的样点值从小到大排序并找到第d小的数值；函数LARGE(I(m)，d)表示将I(m)中的样点值从大到小排序并找到第d大的数值。SMALL(I(m)，d)与LARGE(I(m)，d)称为相对阈值，它们的大小与积分区间2TB内所有样点都有关系，而d值的确定又取决于c值，因此称c为绝对阈值。对于积分限幅法而言，其阈值的确定是由相对阈值和绝对阈值共同确定的。

绝对阈值c的确定取决于Alpha稳定噪声的脉冲性，即主要由特征指数α确定。在不同α值下进行大量的测试，得到对应的最佳的阈值c，再通过二次多项式拟合，得到阈值c与特征指数α的函数关系为

经过上述处理得到函数I′(m)后，去除其中值为0的样点得到函数I(n)，其样点数减少为2TBfs×(1-2c%)。积分区间内的强脉冲噪声点都被剔除，剩余样点的脉冲性并不强，类似于高斯白噪声，均值滤波对高斯噪声具有较好的抑制作用，因此可用求均值方法对剩下的去除脉冲性的噪声进行平滑处理，即

在得到平均值Im后使用图1中所示的判决器进行判决就可解调出最终结果。判决规则：当Im>0时，a2k=1；当Im<0时，a2k=-1。

对于正交支路与同相支路的处理方式一样，得到Qm后进行判决。当Qm>0时，a2k+1=1；当Qm<0时，a2k+1=-1。

3 仿真结果

文献［8］提出的改进分支度量的MSK最大似然解调法是目前性能最好的解调方案，下面将本文提出的积分限幅的MSK正交相干解调与之进行对比，分析二者的解调性能。

对于改进分支度量的MSK最大似然解调，主要根据MSK信号具有相位连续性的特点，在所有可能的相位路径中利用维特比算法［7］找到条与发送序列对应的相位路径最相似的路径，其对应的码元序列即为解调结果。

在高斯白噪声情况下通常采用相关测度来计算分支度量，但是在Alpha稳定噪声下需要对分支度量的计算表达式进行改进，由文献［8］可知第k个码元的分支度量为

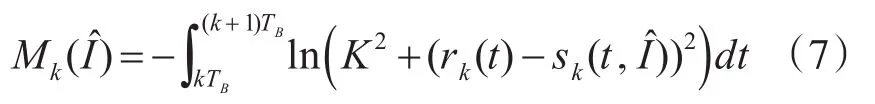
其中rk(t)为接收信号，为发送序列为时对应的发送序列，K是特征指数α的函数，根据经验K取如下式：

得到每个码元的分支度量表达式后，采用维特比算法来执行最大似然序列检测得到解调序列。

由于Alpha稳定噪声为非高斯分布模型，不存在基于第二矩的功率，所以方差这一统计量失去了意义，传统的信噪比公式不适用于Alpha稳定噪声下的信号。当α<2时，采用Alpha稳定噪声的几何功率，表达式如下：

其中，Cg=exp(Ce)≈1.78，Ce是欧拉常数。根据上述几何功率的定义，信噪比Eb/N0计算如下［8］：

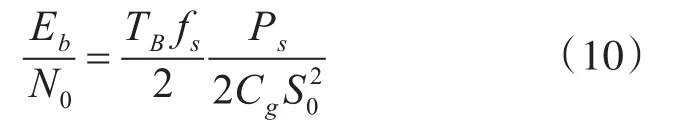
其中Ps为信号功率。

对于VLF通信中的Alpha脉冲噪声，通常假定α>1，因此在下文的讨论中Alpha稳定分布的特征指数范围为1<α<2。下面改变Alpha稳定噪声的参数α，将改进分支度量的最大似然解调与积分限幅的正交相干解调两种方法进行对比。在这里分别设置α=1.1，1.5，1.9，仿真条件如表1所示。

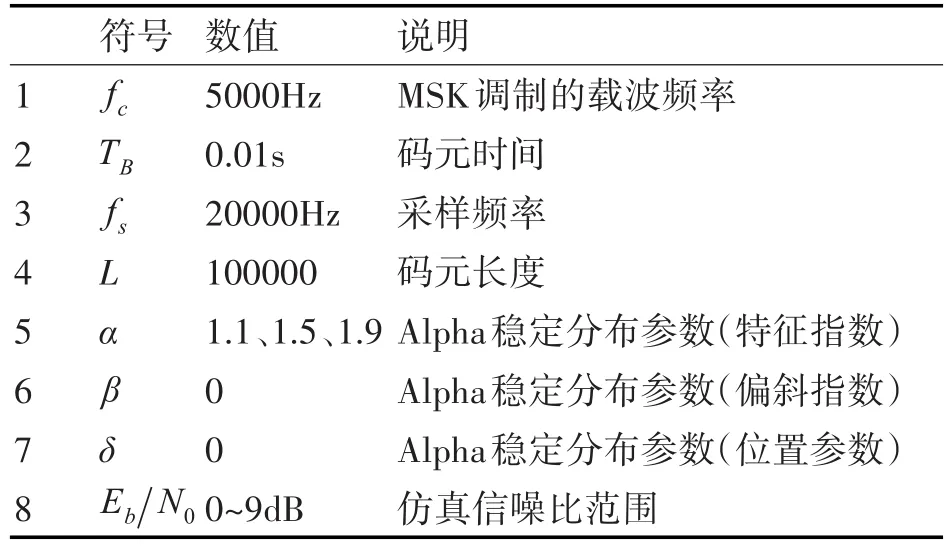
表1 Alpha稳定噪声下MSK信号解调参数设置

Alpha稳定分布的尺度参数γ可由表1中的参数和信噪比Eb/N0计算得到的，根据式（9）可以得到尺度参数γ的表达式如下：

其中S0的值可由式（10）计算得到。

当α=1.1，1.5，1.9时，仿真结果分别如图3～5所示。

图3 α=1.1时积分限幅的正交相干解调与改进分支度量的最大似然解调误码率曲线

图4 α=1.5时积分限幅的正交相干解调与改进分支度量的最大似然解调误码率曲线

图5 α=1.9时积分限幅的正交相干解调与改进分支度量的最大似然解调误码率曲线

由图3可知，在α=1.1的噪声情况下，信噪比较低时积分限幅的MSK正交相干解调的误码率性能优于改进分支度量的最大似然接解调，但在信噪比较高时改进分支度量的最大似然解调法的误码率性能更好。由图4、图5知，在α=1.5和α=1.9的噪声情况下，积分限幅的正交相干解调算法的误码率性能都优于改进分支度量的最大似然解调算法。同时还可以观察到随着参数α的减小，误码率性能变得更好，这是因为α越小，脉冲噪声的能量就越集中在脉冲上，而解调方法的主要目的就在于抑制脉冲噪声，因此就可以抑制大部分噪声能量。

通过仿真对比结果以及理论分析可以发现本论文提出的积分限幅的MSK正交相干解调法相对于改进分支度量的最大似然解调法性能更优。在解调性能上，积分限幅的MSK正交相干解调误码率低；在时间复杂度上，积分限幅的MSK正交相干解调的算法实现简单，运算速度也更快，在码元数量很大的情况下优势更加明显；在空间复杂度上，积分限幅的MSK正交相干解调所耗费的内存空间比最大似然解调要小很多，而最大似然法需要开辟大量的存储空间来储存路径。

4 结语

本文提出的积分限幅的MSK正交相干解调算法在Alpha稳定噪声下可以获得较低误码率的原因主要在于两点，一是前置了码变换器，二是在正交相干解调单元的积分部分采用了改进的限幅法。通过对比可以看到在解调性能、算法时间复杂度、空间复杂度三个方面，积分限幅的MSK信号正交相干解调法都优于改进分支度量的MSK最大似然解调。