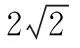基于数学运算素养下“立体几何初步”的教学——“直观图画法”课堂教学设计与感悟

江苏 郑宝生 邓 蓉

数学运算是数学活动的基本形式,也是一种演绎推理.数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.它不只是数字或字母的运算,主要表现为:理解运算对象,掌握运算法则,探求运算思路,求得运算结果.它有助于促进数学思维发展,形成一丝不苟、严谨求实的科学精神.立体几何是研究点、线、面及其位置关系的,重点在于培养学生的空间想象能力,在“立体几何初步”教学中如何落实数学核心素养,立足于数学运算的视角下怎样设计课堂教学,值得我们思考.本文结合“直观图画法”的课堂教学设计谈一谈个人的看法.

一、数学内容分析

立体几何是研究现实世界物体的形状、大小和位置关系的,而“立体几何初步”的学习,恰恰是为学生提供立体几何方面的知识基础,探求解决立体几何问题的方式方法以及公理化体系.而“直观图画法”是学习立体几何的初级门槛,它为“立体几何”的后续学习建立了立体图形的保障.

二、学情分析

学生从小学开始就认识长方体和正方体,接下来了解圆锥和球体,到了初中学习了几种常见的几何体并求其面积和体积,学习了三视图并通过三视图来确定几何体,这给了学生画立体图形以丰富的感性知识,为本节课内容的学习奠定了良好的基础.其实,对于大部分学生来说,他们在初中就已经会画长方体和正方体的直观图,然而他们并不理解每一步操作的合理性,更没有在实际操作中形成优化的、完整的操作程序,所以说对于“直观图画法”的学习既需要思想认识上的理解,又需要实际操作上的掌握.本课施教学生是一所普通高中三星级学校的学生,基础和接受能力不够强.

三、教学策略分析

从教学目标上看,通过情境中的学生活动,增加学生的感性认知;通过问题的提出,探求画水平放置的平面图形的直观图的合理性;通过数学运用,探求任意多边形与其直观图面积的关系;通过归纳整理,求得立体几何图形的斜二测画法.从教学方式上,在直观感知的基础上进行操作确认,在度量计算的基础上探求结论,在推理证明的基础上形成规律.从教学重点和难点的角度出发,重点是掌握几何体的斜二测画法,难点是平面图形与其直观图之间的关系.根据上述学情,侧重于基础,过程教学做得比较细.

四、教学过程

教材采用“苏教版《普通高中课程标准实验教科书·数学》必修2,第一章立体几何初步,§1.1.4直观图画法”.

1.问题情境 学生参与活动

(1)出示一个实物正方体,要求每个学生都把这个正方体画出来,其中让两个学生板演;

(2)让学生相互点评,并尝试提出问题.

【意图】由于小学和初中的知识基础,学生能画出正方体和长方体立体图形,然而他们并不知道为什么要这样画？当然也没有一定的操作流程.

2.提出问题 理解运算对象

问题1:正方体的主视(面)为什么画成正方形,而上下底面要画成平行四边形？

【意图】当学生自己画出正方体的立体图形,但不知道为什么这样操作,这样就产生了认知上的冲突,能更好地激发学生探求其中奥妙的学习热情.

事实上,给学生出示一张正方形纸片,把正方形竖直放置,按照我们看到的原样画出,而水平放置的正方形我们看到的是一条线段,这条线段无法表达它是水平放置的正方形,所以我们需要找到一个好的视角来观察水平放置的正方形,只要站在水平放置的正方形的一个角的上方来观察它,按照近大远小的透视规律,故用平行四边形表达.

问题2:水平放置的正方形我们用平行四边形来表示,画这样的平行四边形有怎样的要求？长与宽的线段各画多少？其锐角应该是多少度？

【意图】引导学生思考,从观察的角度看,其长度不变,而宽度取其一半比较容易计算,同样角度也取其一半为45°,由于同旁内角互补也可以是135°.

问题3:画一个正方形或平行四边形的关键都是确定四个顶点的位置,我们会用怎样的方式来确定平面内的点的位置？

【意图】学生会画正方形和平行四边形,但他们不一定意识到,画正方形和平行四边形其实是确定四个顶点的位置,由于学生能够联想到平面内确定点的位置可以建立平面直角坐标系,类似地画水平放置的正方形的直观图,需要建立夹角为45°或135°的斜坐标系.

3.展示例题 掌握运算法则

例1.画水平放置的正三角形的直观图.

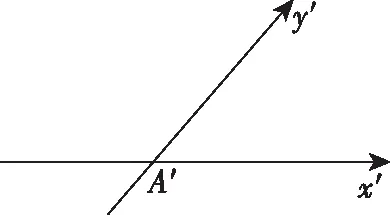
(2)建立平面的斜坐标系,如图2,使∠x′O′y′=45°或135°,写出对应点O′,A′,B′,C′的坐标分别为O′(0,0),A′( ),B′( ),C′( ),并描出三个点.

(3)连接A′C′和B′C′,则三角形△A′B′C′就是△ABC水平放置的直观图.

【回顾】①请把上述的操作过程用语言叙述一遍;

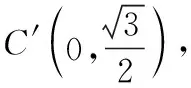
③点P(1,2)在直观图中对应的点P′的坐标是什么？任意点Q(x,y)在直观图中的对应点Q′的坐标是什么？

【意图】通过学生的口述,让学生提炼操作流程,然后通过与平面直角坐标系的类比形成斜坐标系,重点在于让学生理解斜坐标系下点的坐标,这是学生第一次接触的问题,所以在回顾中进行了加强,特别是斜坐标的几何意义,斜坐标中的两个数的绝对值代表哪条线段的长度是关键.

4.数学探究 探求运算思路

问题4:学生练习,画出下列图形水平放置的直观图.

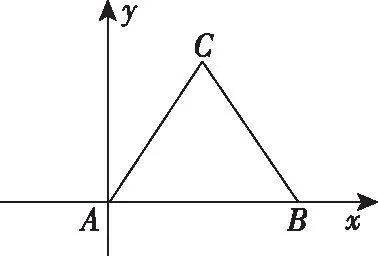
(1)边长为2的正三角形ABC,如图3;

(2)底角为45°的等腰梯形ABCD,其中AB=6,CD=2,如图4.

图4

【回顾】①在上述第一个问题中关键画出哪个点？你能发现△ABC与其直观图△A′B′C′及其对应的元素有怎样的关系？

②在上述第二个问题中关键画出哪些点？等腰梯形ABCD与其直观图梯形A′B′C′D′及其对应的元素有怎样的关系？

③从上述两个问题中,你可以发现怎样的结论？并给出证明.

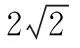
5.归纳整理 形成运算程序

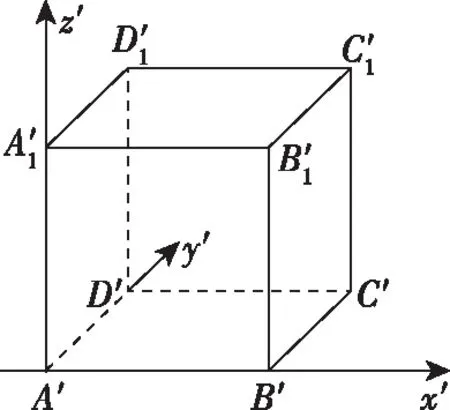
例2.画棱长为2 cm的正方体ABCD-A1B1C1D1的直观图.

画法:(1)以互相垂直的AB为x轴,AD为y轴,AA1为z轴,在正方体ABCD-A1B1C1D1上建立空间直角坐标系;

(2)画其直观图中对应的x′轴,y′轴和z′轴,它们相交于A′,使∠x′A′y′=45°或135°,∠x′A′z′=90°,如图,建立空间的斜坐标系;

【回顾】①口述上述操作过程,并与例1作比较.

②上述画直观图的方法叫作斜二测画法,你认为这里的“斜”是指什么？“二测”又是指什么？

③请归纳直观图斜二测画法的规则.

【意图】通过两个例题的比较容易发现其共同之处,都需要建立对应的两种不同的坐标系,对于平面图形,斜是指y′轴相对于x′轴所成角45°或135°，是斜的,二测是指平行于x轴的线段在其直观图中平行于x′轴,且长度不变;平行于y轴的线段在其直观图中平行于y′轴,且长度变为原来的一半;如果是立体图形,再追加一个条件,平行于z轴的线段在其直观图形中平行于z′轴,且长度不变.这样学生更容易归纳出斜二测画法的操作规则.

6.回顾反思 求得运算结果

(1)两种方法:①画图关键在于描点,怎样把点取得更准确,建立坐标系;②直观图的斜二测画法规则;

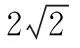
五、三点感悟

从育人的角度看,数学课堂教学要揭示数学本质,开展数学探究,提升学生的数学素养.其一,展示知识的产生过程,揭示数学的本质.对于高中生来说会画正方体,但是不知道为什么这样画,更不知道像写汉字一样还要有一个先后的次序、优化的程序,正所谓知其然不知其所以然,所以我们需要学生在尝试画正方体中提出问题,在问题的解决过程中形成操作的合理性和必然性.画平面图形的直观图关键是确定点的位置,如何确定点在平面的位置,通过直角坐标系建立对应的斜坐标系,在斜坐标系中找出点的位置才是画直观图的本质,这也是学生最熟悉、最容易理解的.