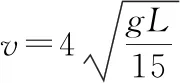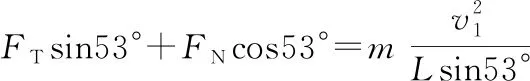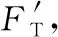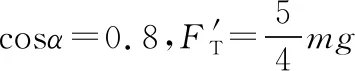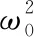圆锥摆模型的拓展与变式

安徽 董廷灿

一、圆锥摆模型

1.结构特点：一根不可伸长的轻绳拴一个可视为质点的摆球，悬挂后在水平面内做匀速圆周运动，如图1所示。

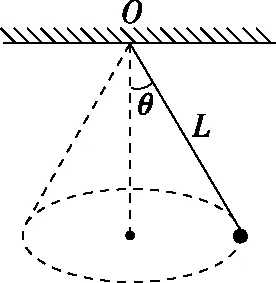
图1

2.受力特点：运动中的小球受到重力和绳对小球的拉力作用，二者的合力提供小球做圆周运动所需的向心力。

3.运动参量：摆线的张力、转动半径、向心力、向心加速度、线速度、角速度、周期。

二、常规问题

【例题】如图1所示，质量为m的小球用长为L的细线拴在天花板上的O点，现将小球拉开，使摆线L与竖直方向的夹角为θ，并使小球在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动)。求：

(1)细线对小球的拉力大小；

(2)小球运动的线速度大小；

(3)小球做圆周运动的角速度及周期。

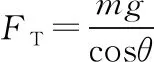
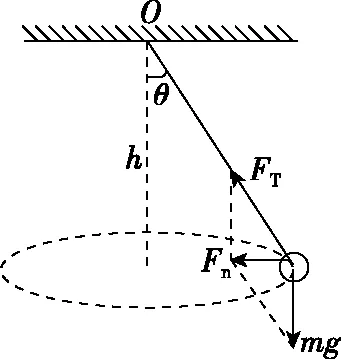
图2

(2)根据牛顿第二定律得

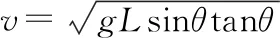
【点评】解决本题的关键在于知道小球做圆周运动向心力的来源，并结合牛顿第二定律进行求解，难度不大。

【拓展】有两根长度不同的轻质细线下面分别悬挂小球a、b，细线上端固定在同一点，若两个小球绕同一竖直轴，在水平面内做匀速圆周运动，相对位置关系分别如下图所示，在两个摆球在运动过程中，小球a的角速度比小球b的角速度小的是

( )

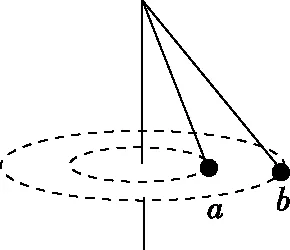
A

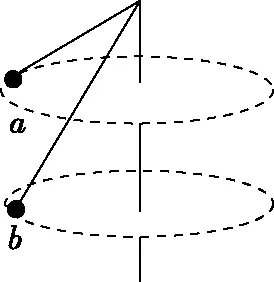
B

C

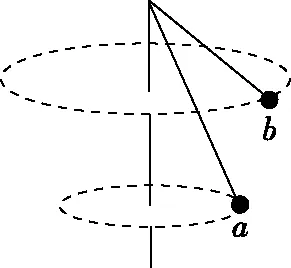
D

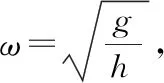
三、变式

1.给圆周摆增加一个面的束缚

【变式1】如图3所示，长为L的绳子下端连着一质量为m的小球，上端悬于天花板上，当把绳子拉直时，绳子与垂线的夹角θ=60°，此时小球静止于光滑的水平桌面上。

图3

【解析】(1)对小球受力分析，作出受力分析图如图4，根据牛顿第二定律得

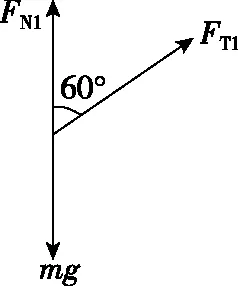
图4

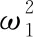
mg=FN1+FT1cos60° ②

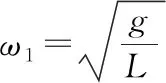
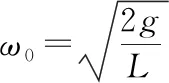
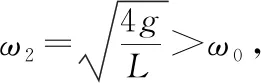
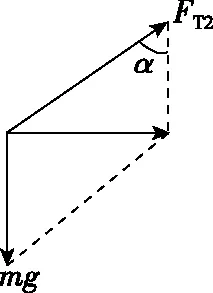
图5

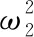
mg=FT2cosα④

联立③④解得FT2=4mg

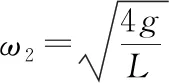
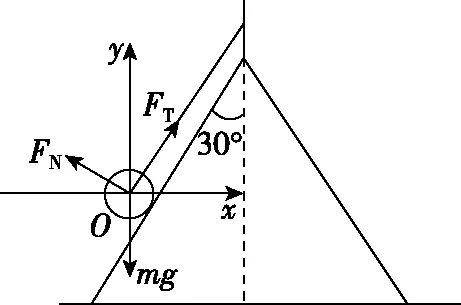
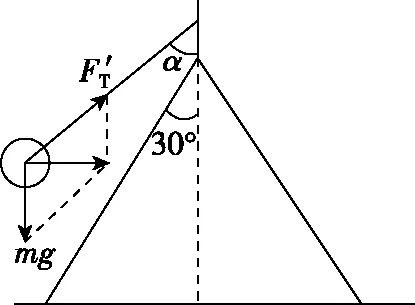
【变式2】如图6所示，一个光滑的圆锥体固定在水平桌面上，其轴线沿竖直方向，母线与轴线之间的夹角为θ=30°，一条长为L的绳(质量不计)，一端固定在圆锥体的顶点O处，另一端拴着一个质量为m的小物体(物体可看作质点)，物体以速率v绕圆锥体的轴线做水平匀速圆周运动。

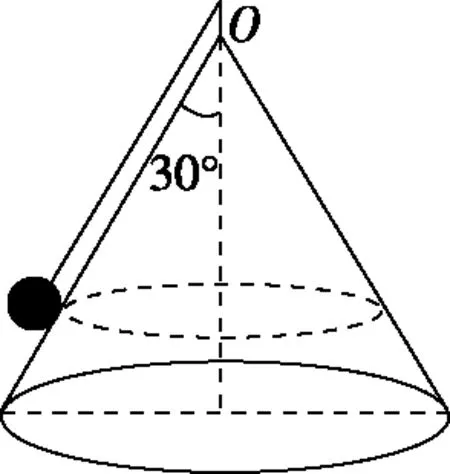
图6

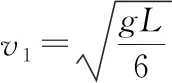
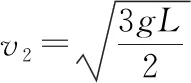
【解析】小球离开圆锥面的临界条件为圆锥体对小球的支持力FN=0，如图7所示，设此时小球的线速度为v0，则

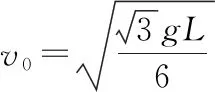
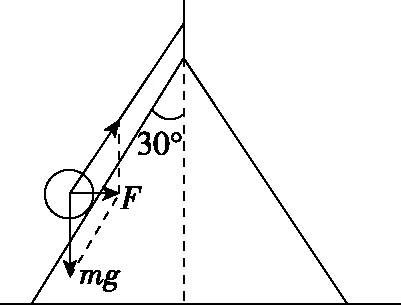
图7

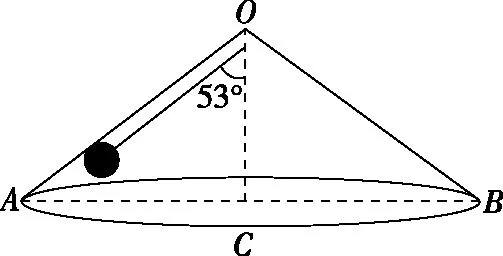
(1)因为v1

FTcos30°+FNsin30°=mg

图8

(2)因为v2>v0，小球离开圆锥面，对小球受力分析如图9所示，有

图9

【点评】变式2与题根相比，增加了一个外侧面的束缚；分析受力、确定向心力来源、抓住小球不脱离锥面的临界状态、求出小球对圆锥面恰好无压力时线速度的大小是解决本题的关键。解题时，需先求出物体刚要离开锥面时的线速度，此时支持力为零，根据牛顿第二定律求出该临界线速度。当小球的线速度大于临界线速度，则小球离开锥面；当小球的线速度小于临界线速度，小球仍受到圆锥面支持力。

【变式3】将一个透明玻璃漏斗倒扣在水平桌面上，如图10所示。OC⊥AB，∠BOC=53°，一条长为L(L

图10

(1)小球的线速度v多大时，小球与漏斗之间刚好没有挤压；

【解析】(1)当小球与漏斗之间刚好没有挤压时，小球只受重力和绳的拉力，根据向心力方程有

(2)因为v1>v，小球挤压漏斗，漏斗对小球的弹力FN≠0，设绳子拉力为FT。

竖直方向FTcos53°-FNsin53°=mg

解得FT=2mg

【点评】变式3与例题相比，增加了一个内侧面的束缚；分析受力、确定向心力来源、抓住小球不脱离漏斗的临界状态、求解出小球对漏斗内侧恰好无压力时线速度的大小是解决本题的关键。解题时，需先求出物体刚要离开漏斗时的线速度，此时支持力为零，根据牛顿第二定律求出该临界线速度。当小球的线速度大于临界速度时，小球挤压漏斗；当小球的线速度小于临界速度时，小球脱离漏斗。

2.给圆周摆增加一条线的束缚

【变式4】如图11所示，两根轻绳同系一个质量m=0.1 kg 的小球，两绳的另一端分别固定在轴上的A、B两处，绳AC长L=2 m，当两绳都拉直时，与轴的夹角分别为30°和45°，小球随轴一起在水平面内做匀速圆周运动，g=10 m/s2。求：

图11

(1)当AC、BC均处于拉直状态，且BC绳拉力恰好为零时，小球的角速度为多少？

(2)当AC、BC均处于拉直状态，且AC绳拉力恰好为零时，小球的角速度为多少？

(3)当小球的角速度为ω=4 rad/s时，上下两根轻绳拉力各为多少？

【解析】(1)当恰好只有AC绳拉紧而BC绳拉直但无拉力时，根据牛顿第二定律可得

解得ω1≈2.4 rad/s

解得ω2≈3.16 rad/s

(3)由(1)(2)可知：当2.4 rad/s<ω<3.16 rad/s时两绳均张紧。当ω=4 rad/s时，AC绳无拉力，BC绳与杆的夹角θ>45°。设此时BC与竖直方向的夹角为θ，对小球有

FBCcosθ=mg

FBCsinθ=mω2LBCsinθ

Lsin30°=LBCsin45°

联立解得FBC≈2.3 N，FAC=0。

【点评】变式4与例题相比，小球多了一根悬线的束缚，但仍然做匀速圆周运动。当小球的转速较小时，AC绳绷紧而BC绳松弛，当小球的转速较大时，BC绳绷紧而AC绳松弛；当AC绳拉直但没有力时，BC绳拉力的水平分力提供向心力，根据牛顿第二定律列式求出此时的角速度，当BC绳拉直但没有力时，AC绳子拉力的水平分力提供向心力，根据牛顿第二定律列式求出角速度，当角速度处于两者之间时，两绳均张紧；当ω=4 rad/s时，BC绳子拉力的水平分力提供向心力，竖直方向分力之和与重力平衡，根据牛顿第二定律列式求解。

【变式5】如图12所示，AC、BC两根绳子系着一个质量为m=0.5 kg的小球，两绳的A、B端分别固定在竖直转动轴上，AC绳长L=2 m，两绳都拉直时与轴的夹角分别为37°和53°，(sin37°=0.6，cos37°=0.8，g=10 m/s2)求：

图12

(1)小球随轴转动的角速度ω=2.5 rad/s时，绳AC、BC的张力分别是多少？

(2)小球随轴转动的角速度ω=3.0 rad/s时，绳AC、BC的张力分别是多少？

【解析】(1)若BC绳子刚好伸直，则

解得ω0=2.5 rad/s

因为ω0=ω，所以BC绳子张力为0；根据牛顿第二定律，有

FACx=mω2Lsin37°=3.456 N

FACy=mg=5 N

(2)当ω=3.0 rad/s>ω0时，BC绳子是伸直的，根据牛顿第二定律，有

竖直方向FACcos37°-FBCcos53°=mg

水平方向FACsin37°+FBCsin53°=mω2Lsin37°

联立解得FAC≈7.24 N，FBC≈1.32 N

【点评】变式5与变式4相比，BC绳子的悬点B由小球重心的上方变为下方，对应的临界条件也有所不同。当小球的转速较小时，AC绳子绷紧而BC绳子松弛，当小球的转速较大时，两根绳子均绷紧；解决本题的关键在于找出BC绳子恰好拉直的临界状态，然后根据牛顿第二定律列式求解。

【变式6】如图13所示，AB为竖直转轴，细绳AC和BC的结点C系一质量为m=2 kg的小球，其中BC=1 m，两绳能承担的最大拉力相等且为F=40 N，小球随转轴以一定的角速度转动，AC和BC均拉直，此时∠ACB=53°，BC⊥AB，ABC能绕竖直轴AB匀速转动，而C球在水平面内做匀速圆周运动(sin53°=0.8，cos53°=0.6，g=10 m/s2)(结果保留3位有效数字)，求：

图13

(1)当BC绳刚好拉直时，角速度多大？

(2)当小球的角速度增大时，通过计算判断AC和BC哪条绳先断？当先断的绳刚断时，角速度多大？

(3)一条绳被拉断后，为了让小球能够做圆周运动，则小球的最大线速度为多少？

【解析】(1)当BC绳刚好拉直时，小球受AC绳的拉力FAC和重力mg，对小球有：

水平方向FACcos53°=mω2·BC

竖直方向FACsin53°=mg

由以上方程解得ω≈2.73 rad/s

(3)当BC绳刚好拉直后，AC绳和BC绳上的拉力分别为FAC和FBC，对小球有：

竖直方向FACsin53°=mg

水平方向FBC+FACcos53°=mω2·BC

当小球的加速度增大时，绳AC的拉力FAC不变，绳BC的拉力FBC增大，所以绳BC先断；由题意可知当FBC=F=40 N时，绳BC被拉断，由以上方程化简可得此时的角速度ω≈5.24 rad/s。

(3)当BC绳被拉断后，设AC绳与竖直方向的夹角为α，则FACcosα=mg

由题意可知，FAC的最大值为FACmax=40 N

由以上方程可知α=60°，即当α=60°时，对应线速度最大，则

由几何关系可知AC=1.25 m

由以上方程解得v=4.33 m/s

【点评】变式6与变式4、5相比，BC绳子的悬点B由小球重心的上、下两侧变为等高，对应的临界条件也有所不同。当小球线速度增大时，BC逐渐被拉直，小球线速度增至BC刚被拉直时，对小球进行受力分析，合外力提供向心力，根据向心力公式求解角速度；线速度再增大些，FAC不变而FBC增大，所以BC绳先断；当BC绳断后，AC绳与竖直方向夹角α因离心运动而增大，当小球线速度再增大时，角α随球速增大而增大，当AC也要被拉断时，速度最大，根据向心力公式求解即可。

综上所述，解决好圆锥摆问题的关键在于明确小球的运动情况、受力情况、临界状态，再结合牛顿运动定律、圆周运动知识进行求解。