硬核点过程随机蜂窝网络能量效率优化研究

罗凤琳，赵军辉,2，张青苗

(1.华东交通大学 信息工程学院，南昌 330013；2.北京交通大学 电子信息工程学院，北京 100044)

0 引 言

随着无线技术的广泛普及和快速发展，用户移动终端设备数量呈指数级增长，传统的网络架构已经难以满足用户对数据速率和覆盖概率的需求。因此，超密集网络被认为是5G系统中解决这个问题的创新型技术之一[1-3]。然而，由于微基站的密集部署，超密集网络在提高系统容量和降低传输时延的同时，也带来了一些挑战，如频繁的移动切换、严重的干扰以及大量的基站能耗开销等[4-5]。为了解决上述问题，在云无线电接入网(cloud-radio access network, C-RAN)的保护下[6]，文献[7]提出了一种控制平面和用户平面逻辑分离的新网络架构。该架构的主要思想是将控制信令传输与数据服务传输分离，其中宏基站提供广覆盖和低速率的数据传输以保证连接性和移动性[8-9]，而微基站负责高速率数据传输以保证系统容量需求[10]。这种分离架构有效地解决了频繁切换和控制开销等问题。大部分网络模型研究中，基站是基于泊松点过程(Poisson point process, PPP)分布的，但是基于PPP建模的基站是完全独立随机分布的，没有考虑基站之间存在一定的空间相关性，因此，该分布模型可能会由于2个基站间距离较近而产生强干扰[11-13]。在实际网络部署中，基站的位置分布比PPP分布更加具有规律性。文献[14]提出的硬核点过程 (hard-core point process, HCPP)具有最小距离约束特性，因此，它比PPP更适合用来建模实际基站的位置。

HCPP的复杂性使其难以用于分析，因此，只有少数关于HCPP的研究。在文献[15]中，考虑了相邻基站间的最小约束距离，并分析HCPP下多用户天线蜂窝网络的平均能量效率。文献[16]提出了基于不同的变异系数度量来分析3个常见的HCPP模型的规律性。文献[17]提出了一种易处理的k层下行链路异构蜂窝网模型并推导了中断概率、平均速率等表达式。但该研究只局限于单天线异构蜂窝网建模，没有考虑多天线技术。文献[18]利用大规模用户行为研究超密集网络中能效的优化问题，其中考虑了基站密度，基站发射功率和服务质量的函数关系，但基站是根据PPP建模的，不符合实际。本文采用HCPP建模基站位置，而在现有的基于HCPP模型的随机蜂窝网络中，优化控制/用户平面分离架构中基站节能优化策略尚未得到研究。

在微基站密集部署的异构蜂窝网中，巨大的能量开销是主要问题之一[19]。基站的能量开销主要与基站配备的天线数量、基站分布密度和基站静态功率等因素有关。为了降低能耗，本文考虑将HCPP模型引入控制/用户平面分离的网络架构中，并基于随机几何原理，提出一种基于HCPP的随机蜂窝网络能耗优化方案，该方案联合优化了频谱分配率、天线数量和基站密度3个网络部署参数以获得基站平均能耗的最小值，仿真结果表明，该算法有效降低了基站的平均能耗。

1 系统模型

1.1 HCPP模型

HCPP是一个排斥点过程，其模型中的2个无线节点间存在最小距离约束。本文将基站的位置建模为近似Ⅱ型的Matérn HCPP，该过程是HCPP的特殊模型，表示为∏HCPP。本质上，Ⅱ型的Matérn HCPP是PPP∏HCPP的一次独立的依赖性细化过程[20]。Matérn HCPP∏HCPP可以表示为

∏HCPP={x∈∏PPP:Φ(x)<Φ(x*)，

x*∈B(x,r){x}}

(1)

(1)式中：Φ(x)为∏PPP中位置为x的基站标记值；B(x,r)是以x为中心，以r为半径的圆形区域。

HCPP的基站分布和控制/用户平面分离的网络架构如图1。图1a中的点均代表随机蜂窝网络中基于PPP所分布的基站，基站密度为λP。在基站间设置最小距离约束后，选出满足约束要求的点并标记成实心点。这些点代表基于HCPP分布的基站，基站密度表示为λ。剩下的空心点代表不满足约束要求则被舍弃的基站。

在现有的研究中，已经得到了HCPP模型的一阶点密度和二阶点密度[14-15]。一阶点密度代表PPP分布的点在满足2点间最短距离为S的约束条件下保留的点。HCPP模型的一阶点密度公式为

(2)

二阶点密度描述了HCPP模型中2点之间分布的依赖关系。HCPP模型的二阶点密度的表达式为

ζ(2)(μ)=λpφ(μ)

(3)

(4)

(5)

(3)—(5)式中，μ是位于无穷小区域的2点之间的距离。

1.2 控制/数据平面分离架构

本文将HCPP模型引入控制/用户平面分离架构，如图1b。该架构的主要思想是将通信系统的控制平面和用户平面的信息解耦分离，控制平面支持低频带的宏蜂窝，目的是保持可靠的覆盖范围和良好的移动性，而用户平面支持较高频段的微蜂窝以保证较高的容量并提高用户数据速率。用户根据所需数据传输速度的不同来选择接入宏基站或微基站，高数据速率的用户更适合接入宏基站以避免频繁切换的问题和保证信息的可靠传输，低速移动的用户则接入微基站以保证用户所需的高传输速率。由于宏基站和微基站使用的频带不同，因此，本文的研究忽略宏基站与微基站之间同信道干扰。

图1 HCPP的基站分布和控制/用户平面分离的网络架构示意图Fig.1 Illustration of HCPP BSs distribution and C/U separation architecture

1.3 能耗损耗模型

(6)

(6)式中：ηl是功率放大器的效率；Ml是基站的发射天线的数量；Pcl是额外的发射天线电路功率消耗；Psl是基站的固定功率。

2 HCPP的网络能耗优化问题与算法

2.1 问题建模

本文用平均空间速率(average spatial rate, ASR)衡量宏基站和微基站在用户层的性能[18]。ASR与频谱分配比、基站密度和用户的可达速率相关，其中宏基站的ASR反映接入宏基站的用户的数据传输速率，而微基站的ASR反映接入微基站的用户的数据传输速率。其表达式分别表示为

ASRm=βWλmR(Mm)

(7)

ASRs=(1-β)WλsR(Ms)

(8)

(7)—(8)式中，R(Mm)和R(Ms)分别代表宏基站和微基站为用户提供的平均可达速率。根据HCPP的干扰模型[23]，推导出的用户平均可达速率的表达式为

(9)—(10)式中：Pj为信号发射功率；Pt为导频信号功率；v是无线信道的阴影效应；τc是阴影标准差；τn是噪声功率。

本文的目的是在HCPP模型结合控制/数据分离的架构下，联合优化基站密度，天线数量和频谱分配比以最小化网络中的基站平均能耗。因此，结合约束条件，基站平均能耗优化模型可以表示为优化问题P1得

s.t. C1:ASRl≥Gl,l∈{m,s}

C2:R(Ml)≥Rt,l∈{m,s}

C3: 0≤β≤1

(11)

(11)式中：Gm表示控制层的ASR阈值；Gs代表用户层的ASR阈值；Rt是确保通信系统性能的QoS需求。

C2: 0≤β≤1

(12)

根据优化问题P2，本文分别用最优算法和次优算法获得频谱分配、基站密度和天线数量的最优解，并验证算法的有效性。

2.2 最优算法

首先，将频谱分配比β的n+1种情况代入优化问题P2，并分别求出每个β对应的最优的基站密度和天线数量，因此可以得到n+1种最优系统参数组合及基站平均能耗，最后通过穷举法选出最小的基站平均能耗所对应的参数组作为最优解。

优化问题的宏基站最佳天线数可以通过将目标函数对Mm求一阶导后，将导式置零求出。目标函数的一阶导函数为

(13)

(14)

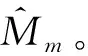
(15)

(16)

通过(16)式可以求得所有可能的宏基站与微基站的最优天线数后，将其代入(7)式和(8)式，可分别求出对应的最优基站密度。将所得的最优天线数和基站密度组代入优化目标函数，通过枚举法可找出使基站平均能耗最低的最优部署参数组。

2.3 次优算法

最优算法由于需要获得所有可能的β对应的基站密度和天线数，因此在计算中需要进行n次比较。在最优算法中，由于β是属于[0,1]的离散变量，因此优化目标函数是一个离散且非凸的优化问题。为了降低计算的复杂度以及将优化问题转化为凸优化问题，本节将β松弛为[0,1]的连续变量，由此可得优化问题P2是关于β的线性函数。此外，可证明优化问题的约束条件都是线性的。因此，在次优算法中，优化问题P2是个凸优化问题。本文进一步根据二分法为优化问题P2提出一种迭代算法。首先将优化的目标函数对β求一阶导，其中一阶导函数为

(17)

将一阶导函数置0，即H(β)=0，可得到最优频谱分配比与基站天线数的函数关系式为

(18)

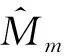
2.4 复杂度分析

对于最优算法以及次优算法的复杂度，本文假设计算中带宽分配比穷举次数为D。由于求解(14)式是采用二分法以获得最佳天线数的唯一解，故其复杂度为O(lbD)。其次，最优算法是通过穷举法线性搜索获得频谱分配比，因此，其复杂度为O(DlbD)。对于次优算法，假设迭代次数为N，则次优算法的复杂度为O(NlbD)。因此可得，次优算法比最优算法复杂度降低D/N倍，即次优算法有效降低了计算基站平均能耗的复杂度。

3 仿真分析

3.1 仿真参数设置

本节对提出的HCPP模型的优化算法的有效性进行分析，证明本文的较低复杂度迭代算法可以实现接近最优算法的性能。此外，在最优系统参数配置的情况下分析了基站密度，基站间的最小距离与基站平均能耗的关系。表1列出了用于仿真的关键参数。

表1 系统仿真关键参数Tab.1 Key parameters of system simulation

3.2 仿真结果

图2为HCPP模型与PPP模型下Gm/Gs与基站平均能耗之间的关系。首先，由图2可知，在同一Gm/Gs下，HCPP模型的基站平均能耗始终小于PPP模型。其次，仿真验证了该低复杂度迭代算法的性能能够接近最优算法的性能。其中，次优算法比最优算法功耗降低了220～400 W/km2，该差值与基线能耗的比值是0.048～0.095。由于该比值低于0.1，故该差值对算法性能的影响可忽略不计。此外，基站平均能耗将随着Gm/Gs的递增而增加，这是因为宏基站的ASR阈值越大，则需要部署更多的高能耗宏基站才能满足所需的吞吐量，因此基站平均能耗也将随之增加。

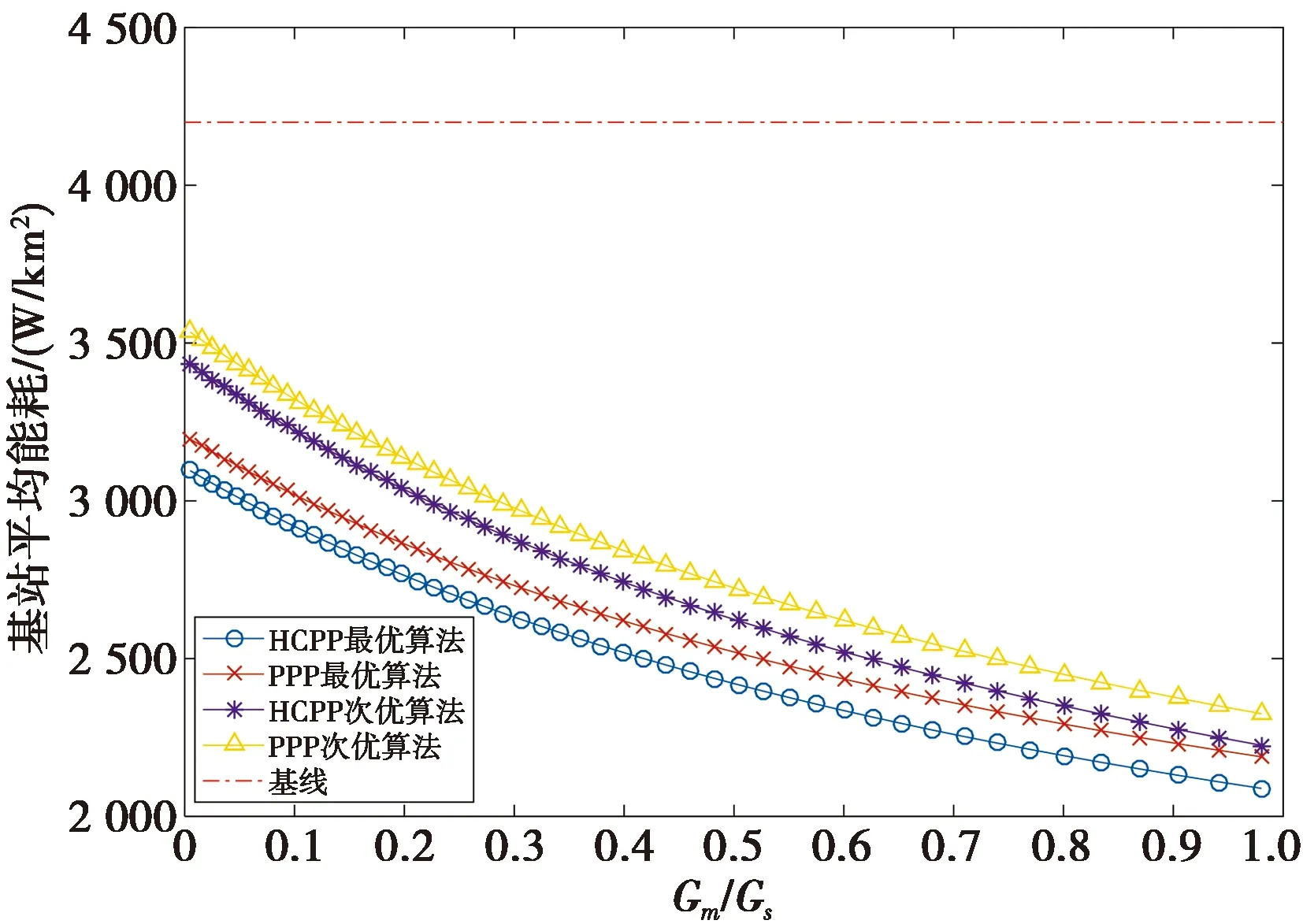
图2 不同算法与基站平均能耗的关系Fig.2 Energy consumption of BSs vs. Gm/Gs

图3说明了在本文所求得的最优系统参数配置下，基站间最小距离在3种不同基站部署密度取值的情况下的基站平均能耗。由图3可以观察到，HCPP蜂窝网络的平均能耗随着基站间最小距离的增加而降低，当最小距离小于0.4 km时，基站平均能耗随着基站密度的增加而增大；当最小距离超过0.4 km时，基站平均能耗将趋于一个稳定值。

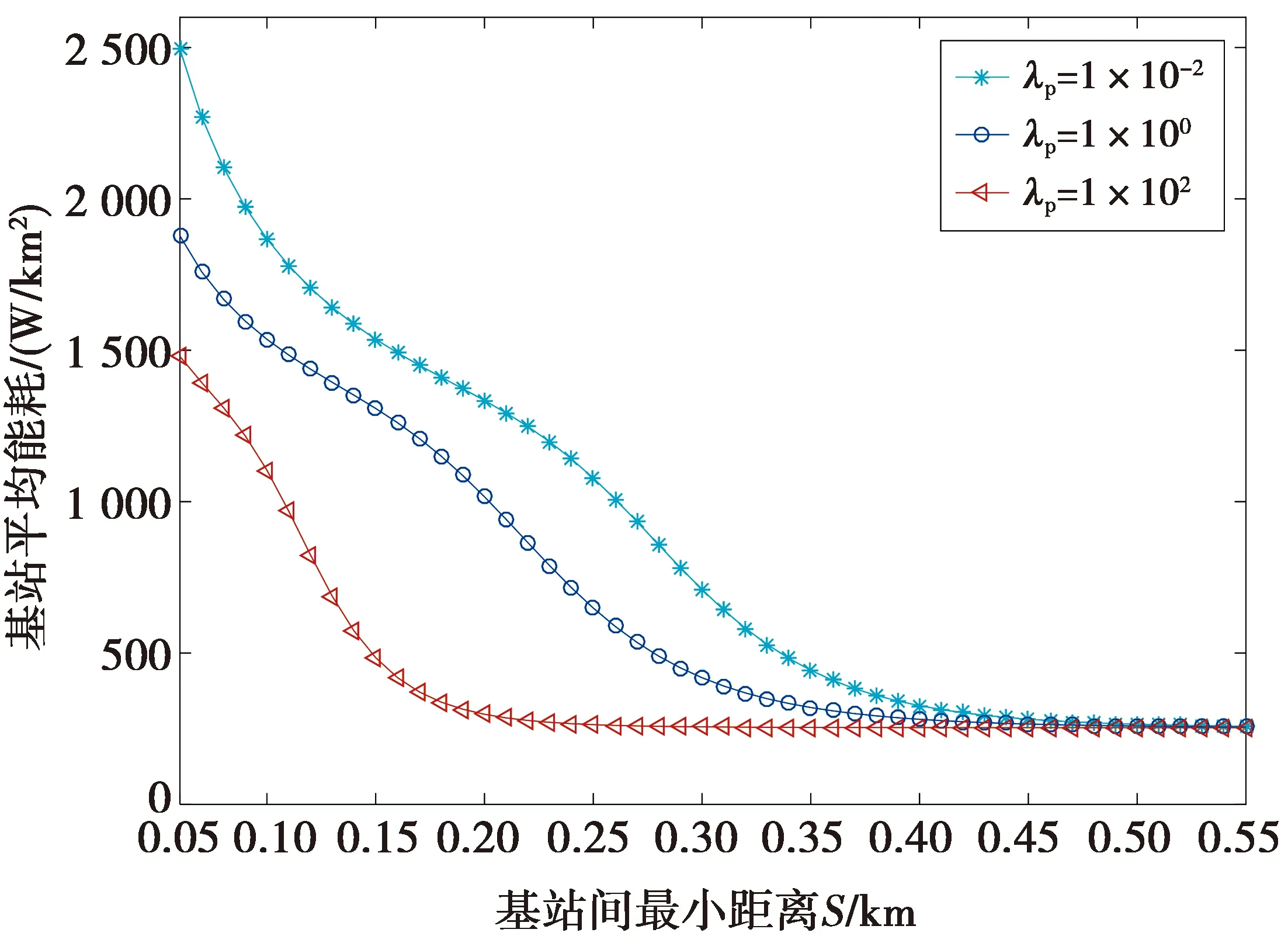
图3 基站间最小距离与基站平均网络能耗的关系Fig.3 Energy consumption of BSs vs. the minimum distance

图4反映了频谱分配比和基站密度随基站间最小距离变化的情况。 随着基站之间最小距离的提高，频谱分配比和基站密度都逐渐增加，因为更高的频率分配比意味着基站之间的距离将增大，并且宏基站占据更多频谱。同时，随着基站密度增加，频谱分配比率变小。然而，当最小距离超过0.5 km时，不同基站密度所对应的频谱分配比将趋于相同值。

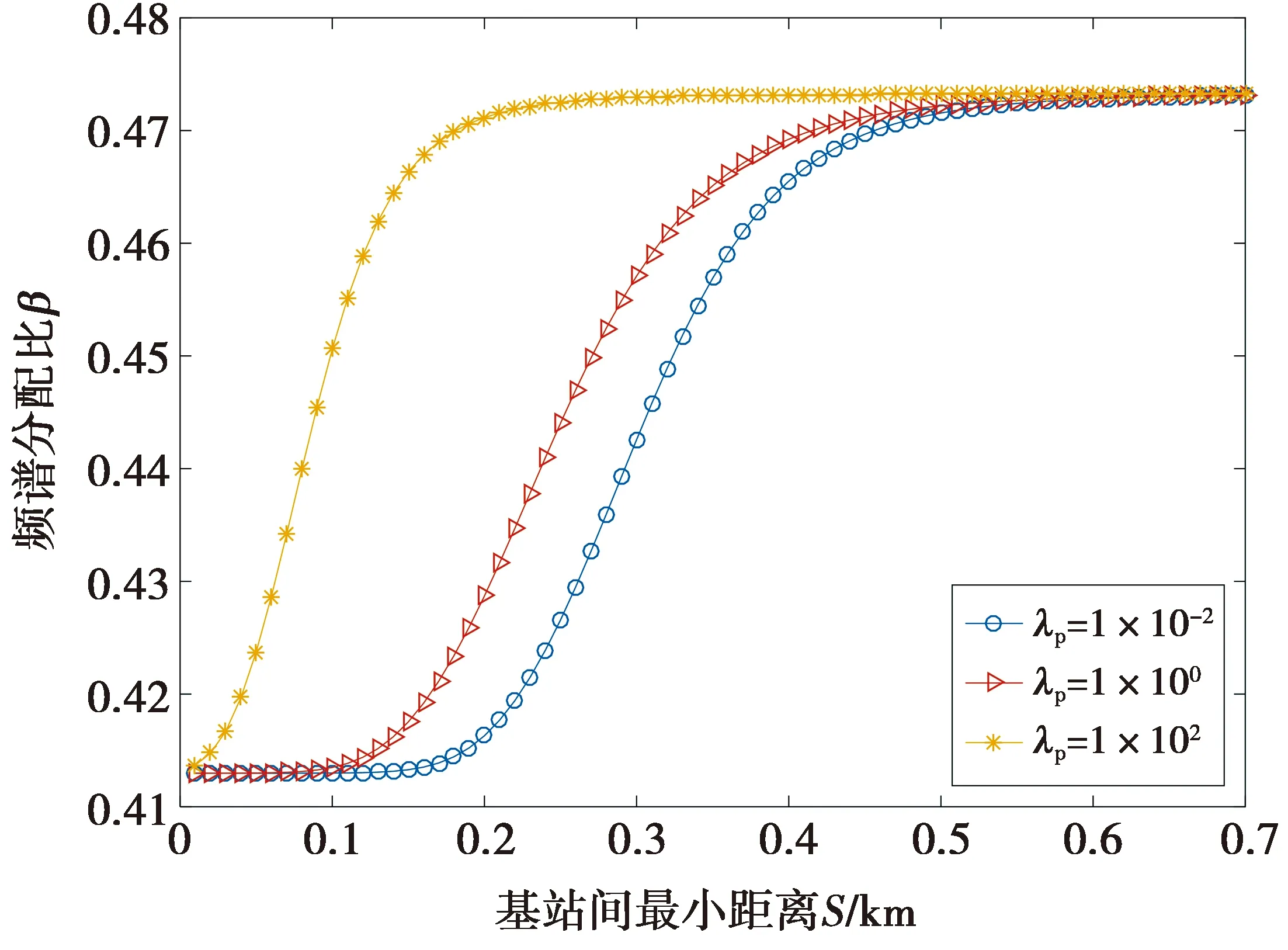
图4 基站间最小距离与频谱分配比的关系Fig.4 Spectrum allocation ratio vs. the minimum distance

图5分析了HCPP蜂窝网络中相对于基站密度和基站间最小距离的基站平均能耗。对于相同的基站密度，基站平均能耗随着最小距离的增加而降低。在不同的最小距离下，HCPP蜂窝网络存在不同的最大能耗值。最大功耗分别为1 009.7，648.1，423.7，334 W/km2，其对应的基站间最小距离分别是0.25，0.3，0.35，0.4 km。最小距离的减小意味基站密度增大，并导致基站吞吐量提高，因此基站平均能耗也随之上升。

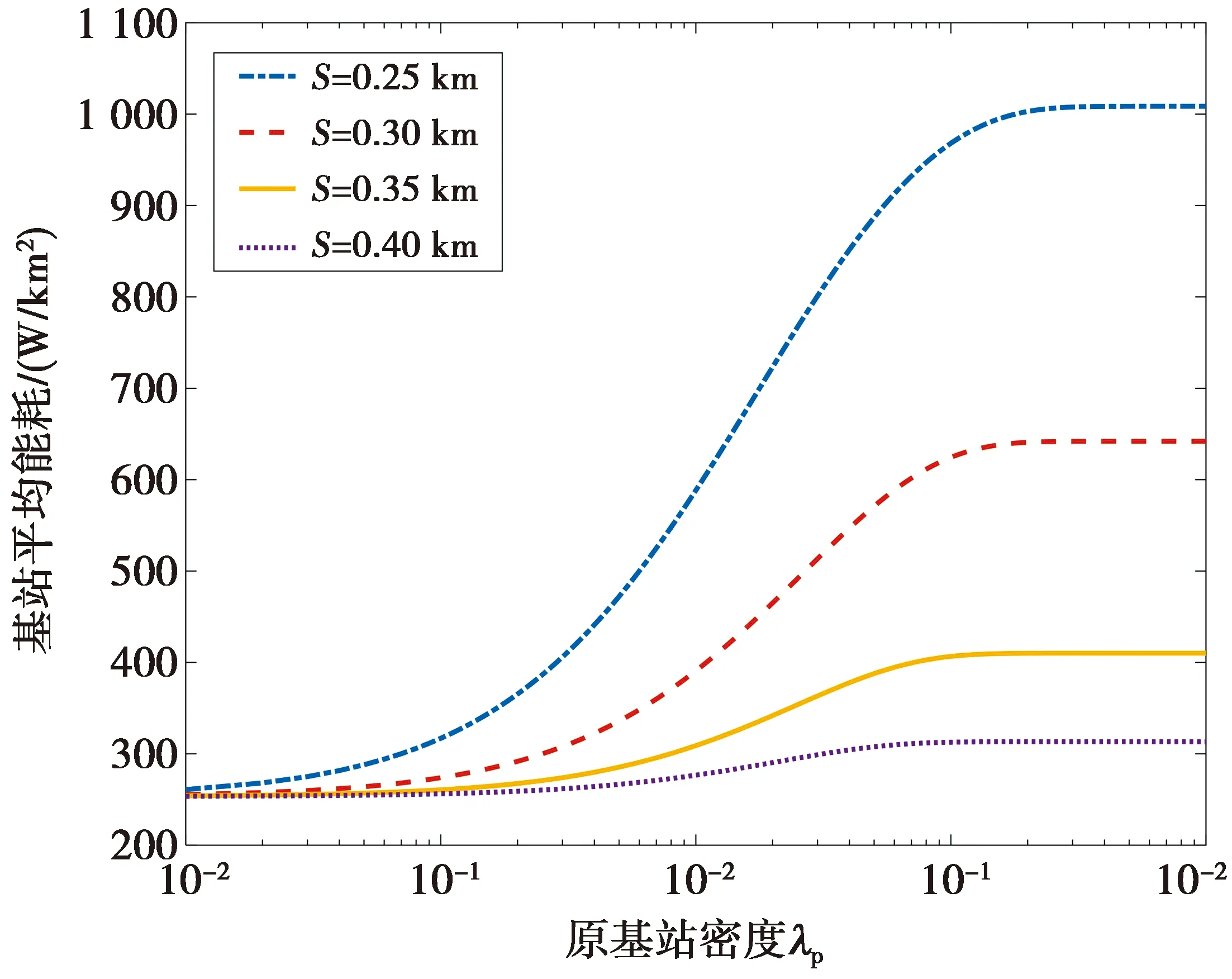
图5 基站密度与基站平均网络能耗的关系Fig.5 Energy consumption of BSs vs. the intensity of BSs

图6给出了基站平均能耗和覆盖率之间的变化曲线。在控制/数据分离架构中，由于控制平面全由宏基站承载，因此系统覆盖率仅与宏基站网络性能有关，即系统覆盖率等于控制层的覆盖率。本文基于文献[19]中给出的覆盖率与基站天线数的函数关系式，仿真覆盖率与基站平均能耗之间的关系。由图6可知，基站平均能耗随覆盖率的增大而提高。

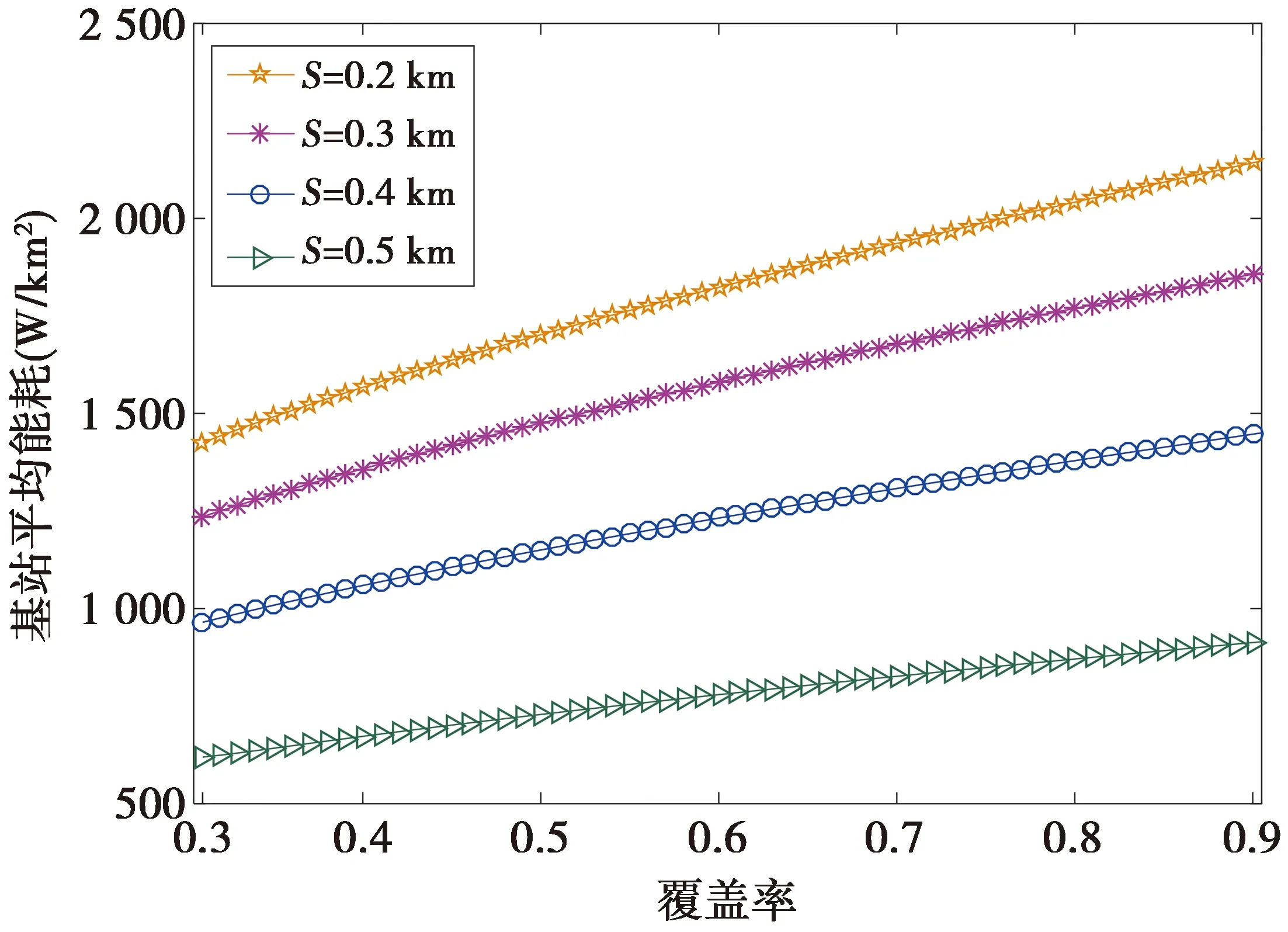
图6 覆盖率与基站平均能耗的关系Fig.6 Energy consumption of BSs vs. the coverage efficiency

4 结 论

本文将具有基站间最小距离约束特性的HCPP模型引入控制/用户平面分离的网络架构，研究了随机网络中能效优化问题。在保证QoS的条件下，通过联合优化基站密度、频谱分配比和基站天线数以最小化基站平均能耗。此外，提出了次优的低复杂度迭代算法来解决问题的非凸性。仿真结果表明，本文所提的次优算法能够逼近最优算法性能。此外，分析表明，基站平均能耗随着基站间最小距离的增加而降低，同时随着基站密度的增加而增大。