基于竞争双深度Q学习的智能电表隐私保护与成本管理
王 峥,郭 彦,聂 峥,庞振江,臧志成,巩永稳
(1.北京智芯微电子科技有限公司 国家电网公司重点实验室、电力芯片设计分析实验室,北京 100192;2.浙江华云信息科技有限公司,杭州 310000)
0 引 言
随着5G、人工智能等技术的发展,传统电网变得更加智能化和泛在化,从而逐渐更新换代为当前热门的智能电网。近年来被业界广泛研究的物联网技术被布局到智能电网中,极大地提升了电力系统对海量数据的处理和分析能力[1-2]。高级计量体系是实现智能电网的重要组件,它依赖于拥有传感、计算、存储、通信等能力的智能电表。智能电表能实现电能的智能管理,已经被广泛部署到包括智能家居、智能楼宇、智能园区等新兴应用场景中。
智能电表应用面临的一个主要威胁是电表数字化和网络化带来的数据泄露问题,尤其对于部分工商业用户,用电数据属于敏感的商业机密。为了降低电表数据泄露的风险,需要采取有效的数据隐藏技术降低智能电表数据泄露的风险。电表数据隐藏技术可以大致分为基于电量[3]和基于负载[4]2类方法。基于电量的电表数据隐藏技术主要通过控制电表所监控的储能设备的充放电功率,使用电输出负载趋近于常数;基于负载的电表数据隐藏技术通过转移用户可控负载的能耗需求,使能耗速率趋近于常数。这2种方法均是从信号和数据处理的角度隐藏智能电表端用电规律的变化,实现电表数据的隐藏。然而,无论使用哪种方法都会增加用电成本的代价[5],因此,如何平衡电表的隐私保护效能和用电成本是一个被广泛关注的问题。
现有的研究主要将智能电表的隐私保护和成本控制建模为一个数学优化问题,并寻找最优的策略权衡性能。文献[6]使用平稳高斯模型建模电力负载,并使用隐形马尔科夫过程建模智能电表的读取过程,探讨了电表负载门限设置与噪声对数据泄露的影响;文献[7]使用动态规划方法求解研究了可充电电池的智能电表隐私和用电成本的平衡问题,传统的凸优化和动态规划方法在解决复杂问题时面临复杂度高、计算僵化等问题;考虑到这个问题,文献[8]使用了Q学习的方法,通过Q表计算和更新学习最优的资源分配策略,提升了传统方法因电表状态空间增加而受限的计算性能;文献[9]基于深度强化学习方法更新Q表,提升了学习的效率,然而当储能设备数量较多时,电表负载较重,上述方法存在过度估计和收敛速度慢的问题,不仅浪费大量的计算资源,也会带来明显的延迟,大大降低系统效能。
本文研究了智能家居场景中智能电表隐私保护与用电成本管理的权衡问题。系统模型考虑了热能和化学能储电设备,并分别对电表数据泄露与家居用电成本建模,并建立了权衡2个指标的目标代价函数。为了解决已有方法存在的问题,本文提出了一种基于深度竞争双Q学习的储能电器功率分配方法。该方法智能调节储能设备功率,隐藏用电电量数据,减少数据被入侵者窃取的概率,实现隐私保护目的;动态优化用电量,减少用电成本,实现成本管理目的。在功率分配的过程中,使用2个具有竞争结构模型的Q神经网络,提升传统深度强化学习的收敛速率,并解决学习过程中过度估计问题。仿真结果验证了本文算法的性能增益。
1 系统模型
本文考虑的智能家居储电系统模型如图1。其中,储电设备表示为集合ψ,总数为N,大致可以分为化学能储电和热能储电2种类型[8]。热能储电设备表示为集合ψT,总数为NT,化学能储电设备表示为集合ψC,总数为NC,满足ψ=ψT∪ψC,N=NT+NC。智能电表利用传感器实时读取2种类型的储电设备的电量数据,同时收集不同类型的储电设备状态参数,实现对家居储电电器的智能感知。智能电表收集、归类和处理储能设备的用电数据,将数据反馈给智能管理单元。智能管理单元通过内置功率控制器连接储电设备的控制电路,实现对储电设备的反馈控制。家庭用户通过智能电表连接到电力运营商,并进一步连接到智能电网。
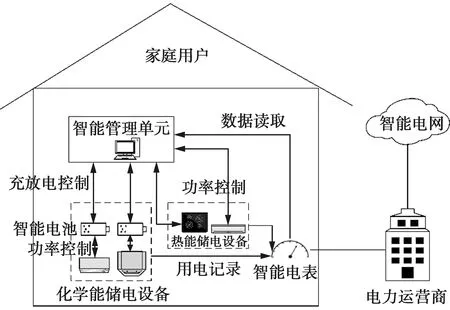
图1 配备储能设备的智能家居系统Fig.1 Smart home system equipped energy-storage devices
本文将系统时间离散化为若干个时间段t∈Ω,Ω为总的时间长度,每个时间段有若干个时隙,时隙长度为Δt。智能管理单元的电力管理策略以时间段为周期执行,也就是在一个时间段t内,智能管理单元收集传感器的采样数据,并按照一定的策略,通过传感器给储电和用电设备下达指令,达到电力管理目的。下面将分别介绍热能储电和化学能储电模型。
1.1 热能储电模型
热能储电设备主要包括用于实现恒温控制的家用电力设备,例如智能暖风系统、电水箱等。热能储电的过程即设备充电,过程中将电能转化为热能进行存储。热能储电过程与设备i∈ψT的热平衡动态有关,表示为[10]
(1)
考虑热能储电设备的实际使用参数以及用电安全等因素,需要设置警戒的最高温度Tmax和最低温度Tmin,额定功率也存在最大值qmax。(1)式的热动态方程参数受以下约束条件限制
(2)
1.2 化学能储电模型
化学能储能设备主要包括安装了可充电智能电池的家用智能电力设备,例如电力汽车、智能电瓶车等。在智能调节中,化学能储能设备i∈ψC的电池电量可以表示为
(3)
(3)式中:qi,t是电池充放电速率,当qi,t>0时处于充电状态,qi,t<0处于放电状态;Ci是电池容量,与设备对电池储存的要求有关。

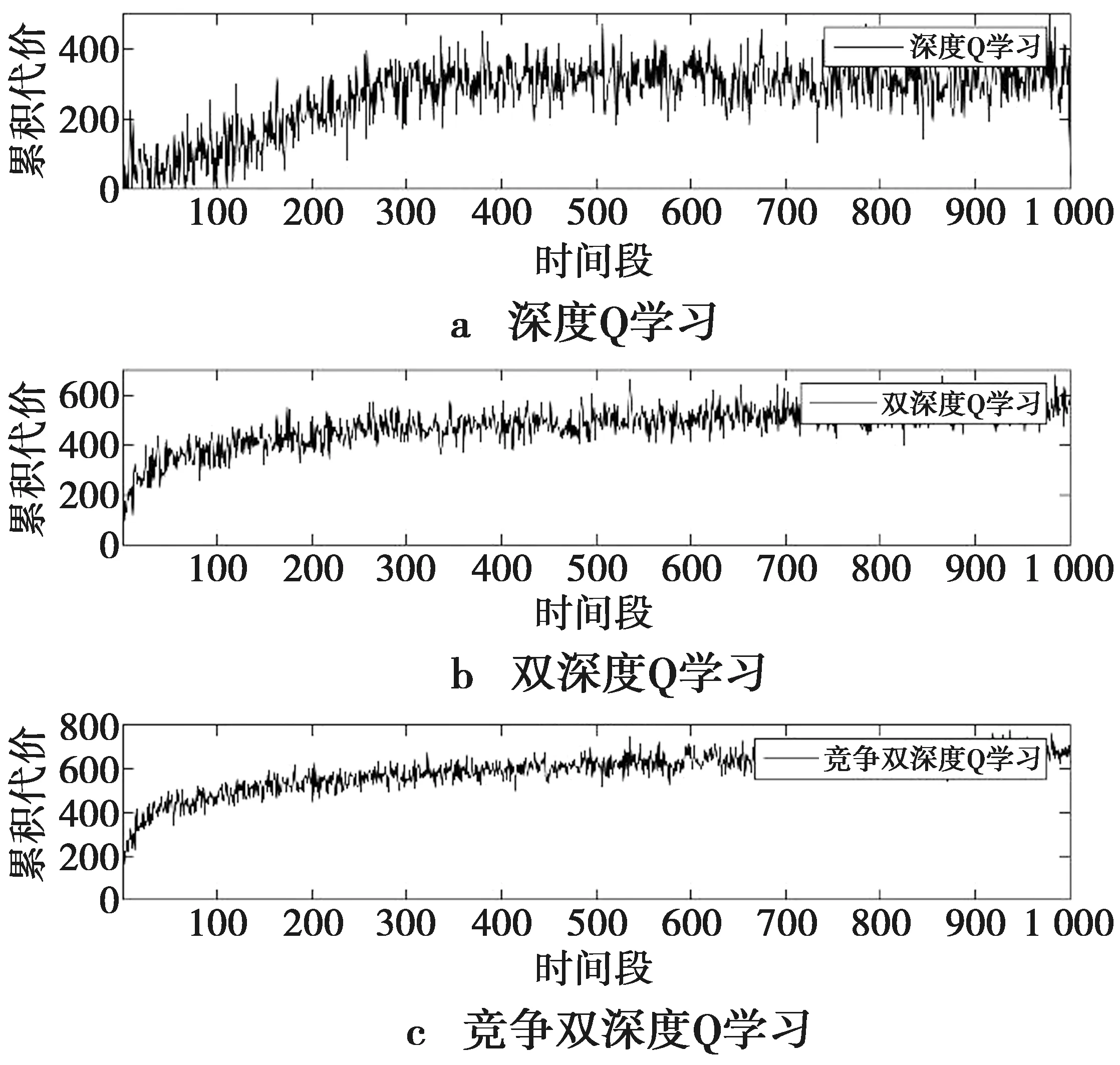
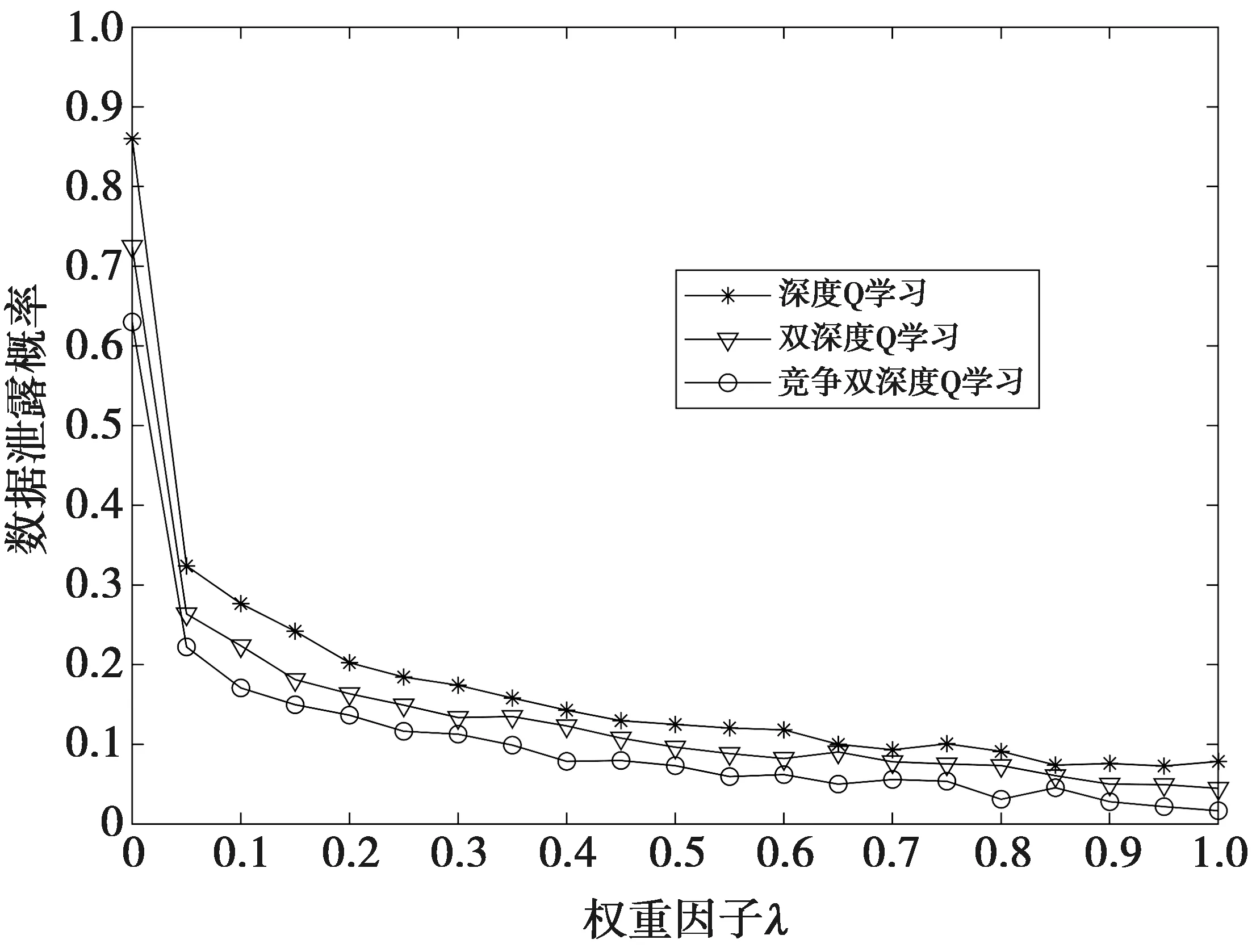
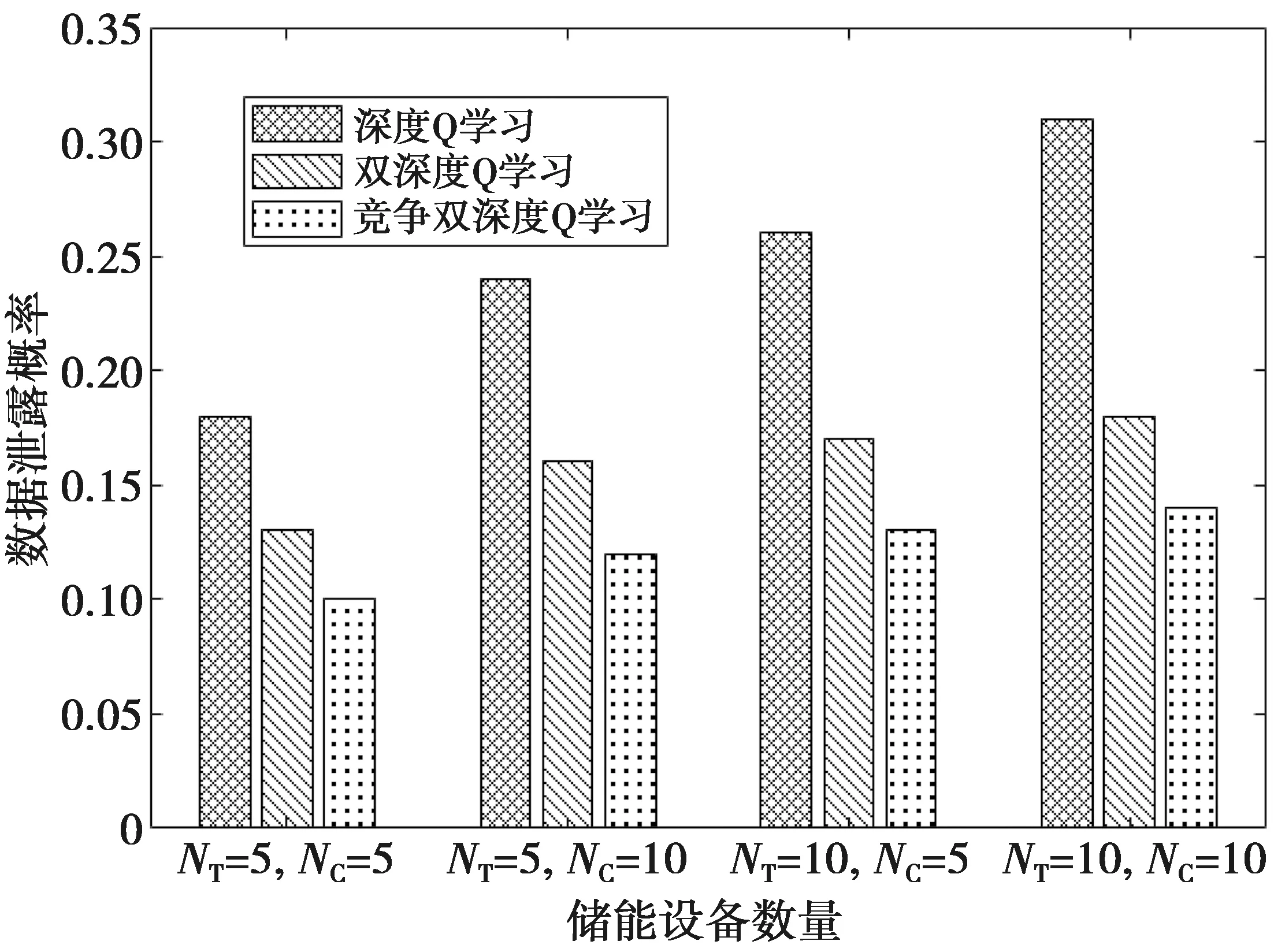
0 0≤Ei,t≤Ci,i∈ψC,t∈Ω (4) 本节从智能电表的数据隐私泄露概率和用电成本量化2方面建立了性能权衡的数学模型。 用电场景的隐私保护主要解决电力数据泄露带来的威胁。本文考虑的场景中,家用电表采用数据隐藏技术,监听者通过读取和还原电力数据引发数据泄露问题。基于信息论在数据泄露问题的广泛应用[12],本文提出了一种基于互信息熵的电力数据泄露概率模型。 如果用X表示家用电表的进过变换处理后的原始离散数据,计算为N个电器在M∈Ω个时隙内用电功率与单位时间的乘积,并做模数转换处理 (5) (5)式中:S(·)是模数转化函数;Y表示窃密者还原的数据,这里采用互信息熵量化数据泄露,表示为 (6) (6)式中:p(Xi)是X的分布概率,与电表数据的编码和处理相关,二进制计数编码方式是简单的方式;p(Yj|Xi)是从原始离散数据转化到还原数据的概率,该概率分布越均匀,表示数据被泄露的概率越小。因此,p(Yj|Xi)与电表的隐私保护处理技术有关。 (7) (7)式中:g(·)表示数据隐藏处理函数。常见的处理方法有加冗余、数据加密、数据映射等。 用电成本与电力单价、电器储电功率、电器使用时间有关。电力公司的电力单价在短期内假定为固定值,记为ξ。用户电器使用功率变化与储电模型类别有关,已经在前面阐述。电器的使用时间与用户习惯有关,电器i运行的时隙数记为τi。用户在M个时隙内的用电成本计算为 (8) 本文的目标是在减小信息泄露概率的同时尽可能优化成本。基于公式Lt和Gt的计算结果,单步目标代价函数表示为 Jt=λLt+(1-λ)Gt (9) (9)式中:λ∈[0,1]是目标代价函数的权重因子。 智能电表连接的用户边缘控制单元能根据电表采集的数据制定策略π,并智能调节用户储能设备的功率参数。策略的制定随着时间而变化,目标代价函数也随电表数值变化。在一个时间段的M个时隙内,需要最小化累计折扣目标代价函数的平均值,表示为 (10) (10)式中:β∈[0,1]是目标代价函数的折扣系数。 传统的深度强化学习具备感知和决策能力,但在现实使用中存在过度估计和收敛慢等问题。本文提出一种竞争双深度Q学习的储能电器功率分配方法。竞争双深度Q学习是一种演进的深度强化学习方法[13-14],它的网络框架结构如图2。通过迭代优化(10)式的性能指标,在隐藏用电量变化的同时尽可能减少用电成本,实现数据隐私保护与用电成本管理的权衡。 图2 竞争双深度Q学习网络框架Fig.2 Framework of dueling double deep Q-learning network 图3 竞争双深度Q神经网络结构Fig.3 Structure of dueling double deep Q-learning neural network (11) 状态空间St是深度强化学习的输入,通过对观测数据进行进一步处理得到。观察2种储能电器的观测空间,额定功率qi,t是共同的参数。同时,通过控制qi,t也能实现对观测空间中其他参数的直接或间接控制。因此,状态空间定义为St={qi,t},i∈N,t∈Ω。 动作空间At是智能管理单元根据现实反馈的观测状态以及反馈做出的决策行为。智能体通过决策动作改变环境状态,逐渐达到优化代价函数的目标。 动作空间At与状态空间St紧密相关,本文的At定义为St的在单位时隙的改变量,表示为Zt={Δqi,t},i∈N,t∈Ω。其中,Δqi,t=qi,t-qi,t-1。假设储电电器的额定功率是按照最小变化单位δΔ的整数m倍进行变换,则Δqi,t可以表示为Δqi,t=m·δΔ。 回报函数以调节环境状态为目标,为训练提供搜索方向。在训练过程中,本文中设立的回报函数与(10)式的目标代价函数一致。 训练过程基于当前的环境状态获得最丰厚的回报,为智能体制定最优的策略,表示为 (12) (12)式中:θt表示深度神经网络权重矩阵。 训练过程分为多个时间片,本文关注每个时间段内的训练目标,即最小化与目标代价函数相关的均方差损失函数 (13) (13)式中:Zt是时隙t的代价估计函数,表示为 (14) 在上述过程中,采用ε-贪婪算法进行学习探索,即在下一个时隙以概率ε采取随机行动,以概率1-ε采取估计值最大Q估计值的行动。神经网络的权值矩阵采用随机梯度下降法进行调整 θt+1:=θt-ν·∇K(θt) (15) (15)式中:ν是学习率,满足ν>0;∇(x)表示对x进行梯度求解运算。 训练过程中,随机选择一个Q网络作为在线网络,另一个Q网络作为目标网络。基于环境状态和回报函数选取动作,并随机选择在线网络,利用目标网络的迭代更新在线网络的Q值。训练算法的具体流程如下。 算法1竞争双深度Q学习网络训练算法 1 初始化环境、仿真器、储存空间Λ 3 for时间段do 5 for时隙do 6 观察并获取St 7 基于Rt和St,使用ε-贪婪算法选择At 8 计算更新Rt+1,St+1 9 将St,St+1,At,Rt,Rt+1存入Λ 10 从2个Q网络中随机选择一个 11 使用神经网络x计算At+1为 12 计算Zt为 14 end for 15 end for 图4展示了3种训练方法的单步目标函数Jt随训练时间段增长的累积变化趋势。可以看出,竞争双深度Q学习能获得最大的累积代价,略大于双深度Q学习,深度Q学习获得的累积代价最小。同时,竞争双深度Q学习的累计代价在变化过程中抖动最小,且变化速度最快,竞争双深度Q学习所需的计算资源和收敛时间段最少。因此,从代价函数的计算、收敛速度这2方面来看,竞争双深度Q能获得更优的性能。 图4 累积代价与训练时间段Fig.4 Accumulative cost with the training episodes 图5展示了用户用电成本与目标代价函数的权重因子之间的关系。总体来看,权重因子越大,表明代价函数更侧重于对隐私泄露的优化,日均用电成本缓慢上升。相比于深度Q学习和双深度Q学习,竞争双深度Q学习能略微降低日均用电成本,表明该方法在多指标的性能优化上更均衡,也能获得更大的增益。 图5 用电成本与目标代价函数权重因子Fig.5 Electricity cost with the weighting factor of target cost function 图6展示了电力数据泄露概率与目标代价函数的权重因子的关系。仿真其他参数设为默认值。当权重因子为0时,家庭电表的用户隐私缺乏保护,有较大的概率泄露隐私。当权重因子大于0时,用户的智能管理单元开始对数据隐私保护进行优化,因此,数据泄露概率急剧下降。然而,当继续增加权重因子时,数据泄露概率下降并不明显。对比3种方法,竞争双深度Q学习有最好的隐私保护性能。 图6 数据泄露概率与目标代价函数权重因子Fig.6 Data leakage probability with the weighting factor of target cost function 图7展示了用电成本与2种储能设备数量的关系。仿真其他参数设为默认值。当热储能和化学储能设备数量均为5时,日均用电成本最小,2种设备数量均为10时,日均用电成本最大。也就是说,日均用电成本与设备的数量整体上呈正相关。对比3种方法,可以看出竞争双深度Q学习在设备数量不同的情况下均能获得更优的用电成本性能。 图7 用电成本与设备数量Fig.7 Electricity cost with the number of devices 图8展示了数据泄露概率与2种储能设备数量的关系。仿真其他参数设为默认值。从图8中可以看出,2种设备的数量增加时,数据泄露的概率增大,可能的原因是更多的设备数增加了数据量隐藏的难度。相比于另外2种方法,竞争双深度Q学习对于抑制数据泄露的方面具有比较明显的优势,表明该方法对智能电表的隐私保护有较强的优化效果。 图8 数据泄露概率vs.设备数量Fig.8 Data leakage probability with the number of devices 本文研究了智能家居场景中智能电表的隐私保护和成本管理问题。在系统中考虑了化学储电和热力储电2种设备,建立了量化的数据泄露和用电成本模型,提出了一种基于竞争双深度Q学习的储电设备功率分配方法,实现了隐私保护和成本管理的权衡。实验结果表明,所提方法在所研究问题上,比基于传统的深度Q学习和双深度Q学习的方法更大尺度地降低数据泄露概率,并降低用电成本。本文仅考虑了单个智能电表,下一步将研究多个智能电表的隐私保护和成本优化的联合管理策略。2 问题建模
2.1 数据隐私


2.2 用电成本
2.3 目标代价函数
3 基于竞争双深度Q学习的功率分配方法

3.1 竞争双深度Q网络结构


3.2 观测与状态空间

3.3 动作空间
3.4 回报函数
3.5 训练算法

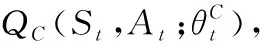

4 仿真分析
4.1 仿真参数设计

4.2 仿真结果分析


5 结 论

