宏微网络中基于后决策状态学习的基站关断节能策略

陈端云，夏炳森，陈卓琳，王威丽

(1.国网福建省电力有限公司，福州 350003；2.国网福建省电力有限公司 经济技术研究院，福州350012；3.重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

随着无线蜂窝网络中用户数目的不断增加及其所需数据速率的不断提高，蜂窝网络的规模也在逐渐扩大，巨大的网络规模和较多的无线设备造成了巨大的能量消耗，这给环境和经济带来了严重的影响[1-2]。为了提高蜂窝网络的环境效益和经济效益，节能减排已经成为当前通信网络的重要设计目标。为了在满足蜂窝网络中日益增加的用户需求的同时减少网络的能量消耗，无线宏微网络已经成为当前的热门研究方向之一[3]。在宏基站覆盖范围内密集部署高容量、低功耗的小基站成为目前在满足用户所需服务质量(quality of service, QoS)的同时降低能源消耗的主要方式[4-6]。

宏微网络中的小基站一般是按照巅峰时期网络的业务水平进行部署的，而不考虑网络业务随着时间动态变化的情况[7]。调查结果表明，每天有超过40%的时间里网络业务量不到巅峰时期业务量的10%，若在网络负载较低时依然开启所有基站，会明显造成网络带宽资源和能量资源的浪费[8-9]。因基站的能量消耗在整个网络能耗中占60%～80%[10]，当网络中的负载水平较低时，关闭利用率较低的小基站可在很大程度上减少网络的能源消耗。

近年来，基于基站关断策略实现网络节能的思想得到了广泛关注。YANG等[11]提出了基于集合覆盖的贪婪式算法通过最小化开启基站数目来达到降低网络能耗的目的。GHAZZAI等[12]设计了基于迭代算法的基站关断和资源分配联合策略在保证用户QoS的同时最小化网络能耗。KUANG等[13]设计了一种联合基站关断、资源分配和干扰协调策略的次优启发式算法以达到减少异构网络能量消耗的目的。但上述研究均忽略了实际网络中业务到达过程的随机性问题，当网络状态改变时，上述算法机制需要重新设计新的解决方案适应当前网络状态。

为了根据网络状态制定动态的基站关断策略，当前部分研究将基于基站关断的节能问题建模为马尔科夫决策过程(Markov decision process, MDP)，根据动态变化的网络环境制定基站关断的序贯策略以达到网络节能的目的。LI等[14]使用MDP刻画业务的动态变化情况并采用基于迁移学习的actor-critic算法获得了能耗-时延折衷的基站关断机制。AYALA-ROMERO等[15]将基站关断和干扰协调联合优化问题建立为MDP并通过近似动态规划来制定满足QoS保证的节能机制。然而，据作者所知，当前基于MDP的动态基站关断策略制定机制均要求系统状态为已知的先验知识，然后进行长时间的行为探索来寻找对应每个网络状态的最佳节能策略，但在长时间的行为探索过程中，算法性能的下降会不可避免。

为了解决MDP模型在求解过程中面临的上述问题，本文引入后决策状态学习算法[16]求解基于基站关断的节能问题，所谓后决策状态即在已知系统状态发生后而未知系统状态发生前的中间状态。后决策状态学习算法的关键优势是可以充分利用基站关断行动执行前已知的网络信息学习关断策略执行后未知的网络状态，从而快速制定出相应的关断策略，在减少算法学习时间和运行时间的同时，提升算法的整体性能。

将宏微网络中的用户根据关联的基站进行分类，当关闭网络中某一个利用率较低的小基站时，接入该小基站的用户会关联到宏基站接受服务，其中宏基站将始终处于开启状态以保证网络的有效覆盖。为了在保证用户服务质量的同时降低异构网络在整个时间周期上的能量消耗，本文建立了时延限制条件下最小化长期平均能耗的数学模型。通过将网络中每个基站的用户数目定义为系统状态，将每个小基站的开/关操作定义为网络行动，本文将基于动态负载变化的基站关断问题映射为CMDP模型。

本文的主要贡献和创新可总结为以下几点。

1)本文引入后决策状态学习算法对CMDP模型进行求解，并推导出了基站关断决策执行前和执行后宏基站和小基站的负载状态；利用已知的决策前状态值函数更新决策后状态值函数直至收敛，得到最优的基站关断节能策略；

2)本文对基于后决策状态学习的基站关断节能算法进行了收敛性分析，证明了该算法可收敛于最优的节能策略。

3)本文通过数值仿真评估了后决策学习算法的性能，并把它和2种经典的增强学习算法(Q学习和实时动态规划算法)进行了对比。仿真结果表明，本文提出的算法不仅收敛速度最快，性能最优，且可在满足时延限制的同时大幅度降低网络的能量消耗。

1 系统模型

本文研究的网络场景是由一个宏基站和部署在这个宏基站覆盖范围内的多个小基站组成的2层宏微网络，如图1。其中，宏基站用于保证网络覆盖，用K表示宏基站覆盖区域下的小基站集合，则小基站的数目K=|K|。将网络覆盖区域内的每个基站编号为k=0,1,…,K，其中，0表示宏基站。把网络中的用户根据关联基站的不同进行分类，将关联宏基站的用户定义为第0类用户，并用x0(t)表示t时刻和宏基站关联的用户个数。将关联小基站k(k=1,2,…,K)的用户定义为第k类用户，并用xk(t)表示t时刻和小基站k关联的用户个数。为了节约网络能耗，可把网络中利用率较低的小基站关闭，当关闭某个小基站k时，第k类用户会转变为第0类用户，此时由宏基站为其提供服务。

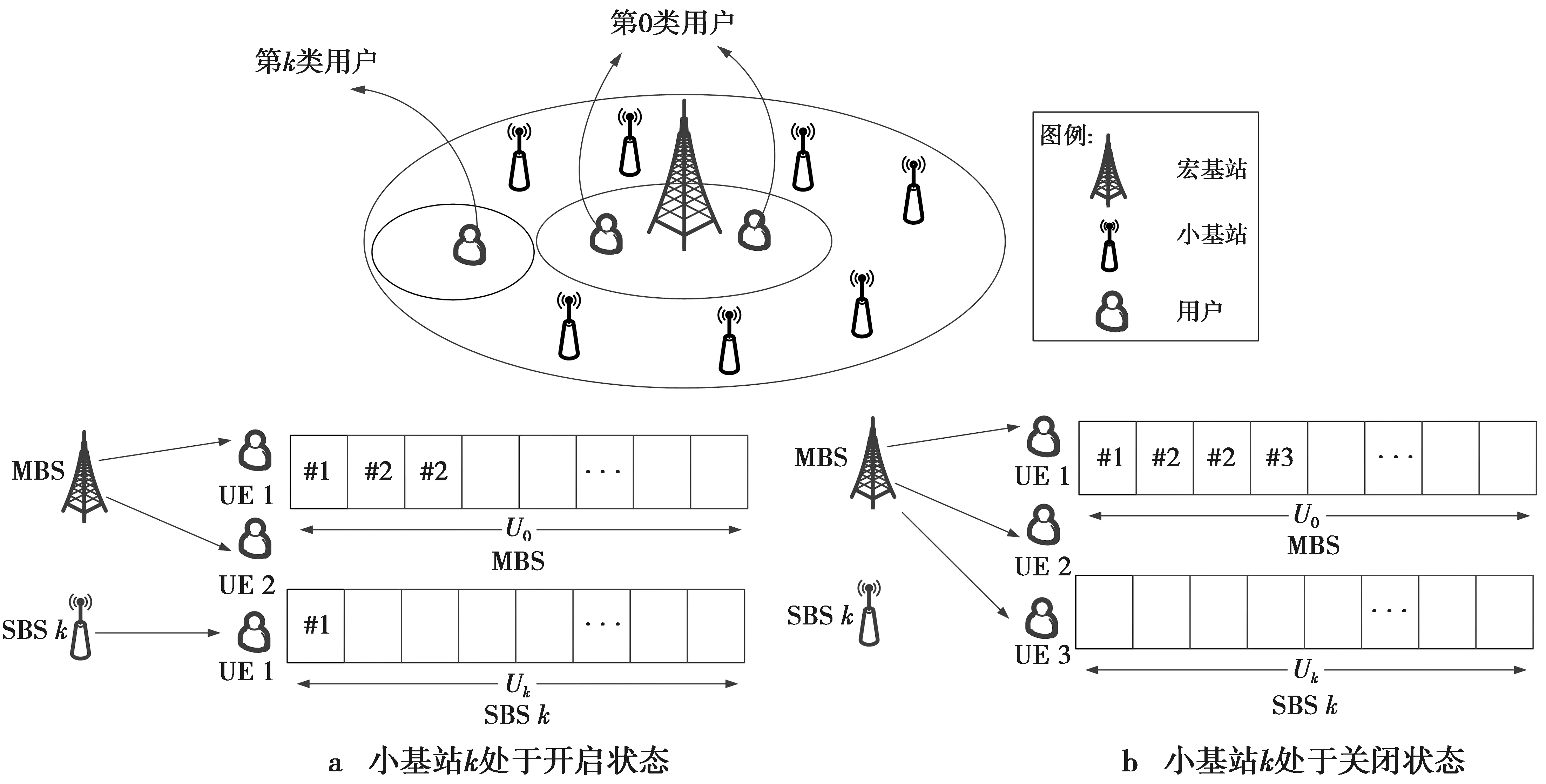
图1 系统模型图 Fig.1 System model diagram

本文考虑离散时间模型，将时间域划分为等长的时隙，每个时隙的时长为T，则第n个时隙就可以表示为nT≤t<(n+1)T,n=0,1,…，因此，本文中的时间t和时隙n表示的意义等价。

采用随机过程x(t)∈X表征时间域上网络负载状态的变化过程，其中，X为网络状态空间，则时间t上的网络负载状态可表示为

x(t)=(x0(t),x1(t),…,xK(t))

(1)

(1)式中，xk(t)表示时间t上第k类用户的个数。根据t时刻网络的网络负载状态x(t)可以制定t+1时刻每个小基站的开/关策略。用y(t)∈Y表示每个时间周期t上小基站的开/关策略集合，其中，Y为网络行为空间，y(t)的具体定义为

y(t)=(y1(t),y2(t),…,yK(t))

(2)

(2)式中，元素yk(t)用来表征小基站k所处的工作状态，若yk(t)=0，表示小基站k处在关闭状态，若yk(t)=1表示其处在开启状态。

2 问题建立

假设rk,i(t)表示第k个基站的第i个用户在时刻t所需要的资源单元数，Uk为基站k包含的资源单元总数，则基站k的负载情况可由(3)式计算得到。

(3)

为了保证网络覆盖，宏基站将一直处于开启模式，则在每个时间周期t上，宏基站的功耗模型可以表示为

(4)

当网络负载水平较低时，可通过关闭一些小基站以达到节能的目的。当小基站处于开启状态时，其功耗模型与宏基站相同，而当小基站处于关闭状态时，其产生的功率消耗可近似为0，故在时间周期t上，小基站的功耗模型可表示为

(5)

虽然关闭某些小基站能够达到节能的目的，但这会不可避免地增加宏基站的服务时延，因基站的时延和基站的队列长度成正比，则宏基站的时延可等价为

(6)

同理，小基站的时延可等价为

(7)

因此，为了在保证用户服务质量的同时降低网络能耗，本文的优化目标是在基站平均服务时延的限制下最小化整个时间域上网络的平均功耗。

根据(4)式和(5)式给出的宏基站和小基站的功耗模型，网络总能耗可表示为

(8)

本文的主要目标是找到一个基站关断策略w:X→Y，在网络状态为xx时为网络选择最佳的小基站工作模式y，其中，y=(y1,y2,…,yK)，当小基站k处于开启模式时，yk的值为1，否则为0。最佳工作模式y可在基站平均服务时延的限制下最小化整个时间域上的平均能耗。基于上述分析，本文的优化目标可表示为

k=0,1,…,K,∀t

(9)

(9)式中：Ω是所有可能的基站关断策略集合；Dth为时延约束门限值。

根据凸优化理论，上述时延受限节能问题的拉格朗日对偶问题为

(10)

(10)式中：β为拉格朗日乘子；g(β,x(τ),y(τ))的完整表达式为

g(β,x(τ),Ω(x(τ)))=

(11)

3 CMDP建模

(11)式建立的拉格朗日对偶模型表示的是网络在某一时刻t上的成本函数，但仅通过最小化时刻t上网络的成本函数无法捕捉网络状态随时间的动态变化情况，实现整个时间域上的能耗最小化。MDP模型是可实现与环境不断交互的一种序贯决策模型，可根据观测系统在每个时间周期上的状态制定相应的策略。因此，为了根据每个时间周期的网络负载状态制定相应的基站关断策略以实现整个时间域上平均能耗的最小化，本文将时延受限的节能问题建立为CMDP模型，如图2。

图2 基于CMDP的基站关断策略原理图Fig.2 Schematic diagram of on/off strategies based on CMDP

基于CMDP的基站关断问题可建立如下概念。

状态空间：{x:∀x∈X}，网络负载状态；

行为空间：{y:∀y∈Y}，小基站关断策略；

转移概率矩阵：{P(x′|x,y)∈A}，P(x′|x,y)代表状态转移概率，定义为当前网络负载状态为x，采取的行动为y，下一时刻网络负载状态为x′的概率；

单步代价函数：{C(x,y)=g(β,x,y)}，单步代价函数定义为每个周期上的成本函数。

在基于CMDP的基站关断模型中，针对每一个负载状态x∈X，都会为其匹配相应的关断策略y∈Y，基于每一对网络状态和网络行动，都有与之相对应的状态转移概率P(x′|x,y)∈A，成本函数C(x,y)。网络控制器感知当前的负载状态x(t)并根据当前负载水平给出相应的小基站关断策略y(t)，基于t时刻的负载状态和关断策略，网络在t+1时刻的负载水平为x′的概率为P(x′|x,y)，与此同时，系统的单步代价函数C(x,y)会反馈给网络控制器，由网络控制器来判定当前采取策略的优劣。

解决上述建立的时延受限长时间平均能耗最小化目标，等价于求出CMDP模型中使当前时隙的成本和未来时期的期望成本之和最小化的行动，因为未来时期成本的不确定性，故未来时期的成本函数需要乘以一个折扣因子来降低它的影响[18]。

本文的最终目标是求得小基站关断策略w，该策略不仅需要实现从负载状态x到基站关断行动w(x)的映射，还需要在保证基站服务质量的同时最小化网络能耗。在CMDP模型中，该目标可通过最小化状态值函数实现，值函数的定义为[19]

(12)

(12)式中，参数γ(γ∈(0,1))为折扣因子。因为问题(9)为长时间平均优化目标，折扣因子可以把网络未来的代价函数以一定的水平对当前基站策略产生影响，从而使得整个时间周期上的平均成本最小化。基于状态值函数，长期平均优化目标(9)的最佳策略w*可通过对下面的贝尔曼方程求解得到

(13)

4 基于后决策状态的在线学习

解决上述贝尔曼方程的经典算法包括值迭代和策略迭代，但这2种方法均需要状态空间和状态转移概率作为先验知识。因用户到达的随机性，实际上很难准确得知网络的状态空间和状态转移概率，因此，本文提出了一种基于后决策状态的在线学习算法，在没有先验知识的条件下动态学习网络的状态空间和状态转移概率，从而获得最优的小基站关断策略。所谓后决策状态即是在已知系统状态发生后而未知系统状态发生前的中间状态，其具体意义如图3。

图3 后决策状态原理图Fig.3 Schematic diagram of the post-decision state

定义λ(t)=(λ0(t),λ1(t),…,λK(t))和μ(t)=(μ0(t),μ1(t),…,μK(t))为t时刻网络用户的到达率和离开率集合，其中，元素λk(t)和μk(t)分别为t时刻第k类用户的到达率和离开率，则用户到达过程和用户离开过程可分别用Ak(t)=E(λk(t))和Dk(t)=E(μk(t))表示，其中，k=0,1,…,K。每个时刻t包含2个负载状态，也即是根据基站关断决策执行前后划分的决策前负载状态和决策后负载状态，假设每个时刻t上的用户到达过程发生在基站关断决策之前，则t时刻的决策前负载状态只和t-1时刻的决策后负载状态以及用户到达Ak(t)有关，为网络已知状态；而t时刻的决策后负载状态和t时刻的决策前负载状态以及基站关断策略执行后的用户转移和用户离开Dk(t)有关，为未知状态。后决策状态学习算法的关键优势就是可以充分利用基站关断行动执行前已知的网络信息减少算法需要学习的知识和运行时间，从而提升算法的整体性能。

(14)

对于宏基站来说，t时刻的决策后负载状态等于t时刻的决策前负载状态加上从关闭小基站转移来的负载再减去离开的用户数；对于小基站来说，若小基站保持开启，则t时刻的决策后负载状态等于决策前负载状态减去离开的用户数，若小基站关闭，则t时刻的决策后负载状态为0。

(15)

(16)

观察上式可知，后决策状态值函数表示未知系统状态的成本期望，把(16)式代入状态值函数(12)可得

(17)

在后决策状态在线学习方法中，后决策状态值函数和拉格朗日乘子会在每个时间周期t上分别根据(18)式和(19)式进行更新。

α(t)Ut(x(t))

(18)

βt+1=βt+εt(D0(t)-Dth)

(19)

状态值函数的更新过程表示为

(20)

算法1基于后决策状态的在线学习算法

2)while TRUE do

4)针对当前的网络状态x(t)执行关断策略y(t)，并根据(20)式更新Ut(x(t))；

6)更新拉格朗日乘子:βt+1=βt+εt(D0(t)-Dth)；

8)end while

5 后决策状态学习算法的收敛性分析

将(18)式—(20)式联合可得到

βt+1=βt+εt(D0-Dth),β∈[0,L]

(21)

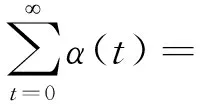
(22)

根据文献[20]可知，和后决策状态的更新速率相比，拉更朗日乘子的更新速率要慢得多，且文献[21]已经证明本文提出算法的收敛性等价于受限常微分方程(ordinary differential equation，O.D.E.)的收敛性，其中和(21)式相关联的受限O.D.E.为

(23)

(24)

6 仿真分析

为了验证本文提出的基于后决策状态学习基站关断算法的性能，在MATLAB平台上建立了一种较为典型的2层宏微网络，该网络由一个处于中心位置的宏基站和部署在这个宏基站覆盖范围内的12个小基站组成。具体仿真参数如表1。

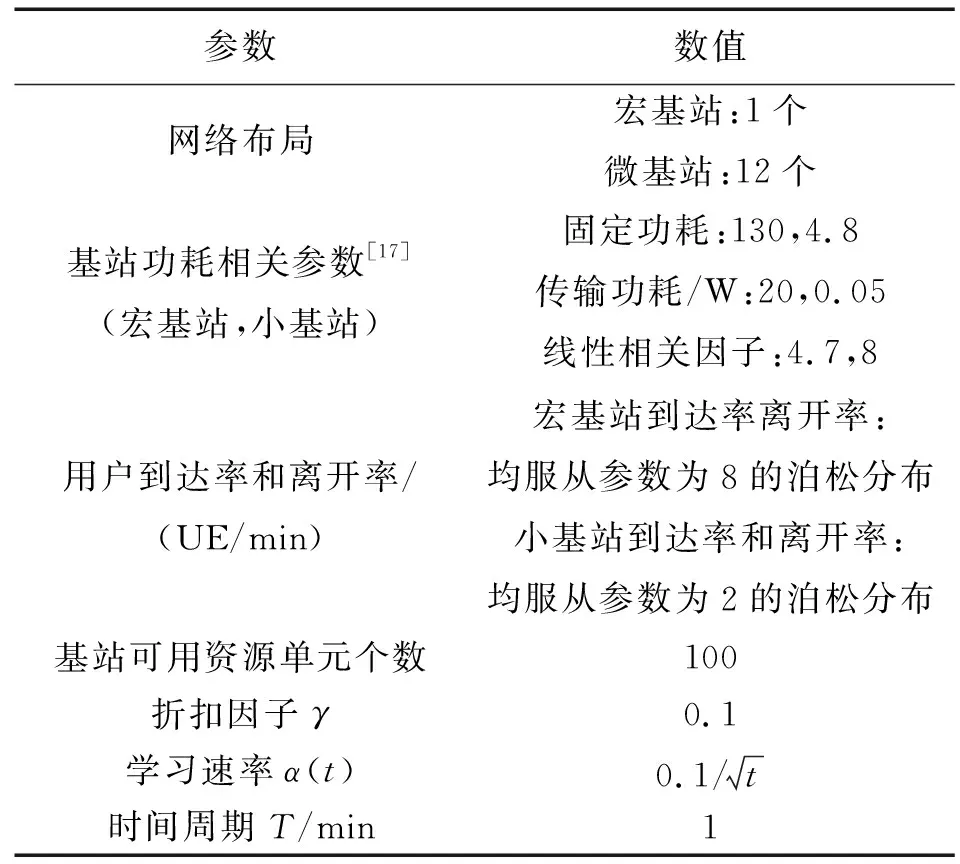
表1 仿真参数Tab.1 Simulation parameters

为了充分验证本文提出的基于后决策状态学习节能算法的有效性，本文将其和另外2种算法进行了性能对比。

1)Q学习[16]：Q学习是一种无模型的增强学习算法。该算法不需要状态转移概率和效用函数的先验知识，但其收敛速度较慢；

2)实时动态规划[16]：实时动态规划是一种基于模型的在线学习算法。当网络执行实时动态规划时，学习智能体首先构建一个潜在MDP的统计模型，然后在这个统计模型中使用过去的经验更新状态转移概率。因此，该算法要求MDP的状态空间是已知的。

图4给出了本文提出的基于后决策学习的节能算法和基于Q学习和实时动态规划的节能算法的收敛对比图。观察图4可以看出，后决策学习因引入了中间状态获取每个时间周期里系统动态的已知部分，故其收敛到最佳性能的速度最快。此外，本文提出的基于后决策学习的节能算法达到的节能效果也比基于Q学习和基于实时动态规划的节能算法要好。由此验证了本文提出的基于后决策学习的小基站关断算法在收敛速度和节能效果上的有效性。

图4 3种节能算法的收敛对比图Fig.4 Convergence comparison among threedifferent energy-saving algorithms

为了进一步验证本文提出的基于后决策状态学习的基站关断节能策略的性能，我们进一步将其与基于Q学习[22]和动态规划[23]的基站关断节能策略在不同宏基站到达率下的能量消耗进行了对比，对比结果如图5。由图5可以看出，本文提出的基于后决策学习的节能算法达到的节能效果比基于Q学习和基于动态规划的节能算法要好，这是因为本文提出的算法可以充分利用基站关断行动执行前已知的网络信息学习关断策略执行后未知的网络状态，从而快速制定出相应的基站关断策略，避免了长时间的行为探索过程中算法性能的下降。

图5 3种节能算法的性能对比图Fig.5 Performancecomparison among threedifferent energy-saving algorithms

图6给出了不同时延条件限制下拉格朗日乘子随时间周期变化的收敛图。图6中仿真了当宏基站的队列长度限制分别为10，15，20时，拉格朗日乘子的收敛趋势。由图6可知，在经过大约500个时间周期后，3种时延限制下的拉格朗日乘子均趋近于收敛。此外，观察图6可知，网络对时延限制越严格，拉格朗日乘子的值就越大。这是因为拉格朗日乘子决定了时延限制在优化目标中所占的比重，严格的时延限制需要通过增加拉格朗日乘子的值实现。

图6 不同时延限制下的拉格朗日乘子收敛图Fig.6 Convergence of the Lagrangian multiplierunder different delay constraints

图7给出了小基站开启数量和宏基站用户到达率之间的相关关系图。观察图7可知，当网络中宏基站用户到达率增大时，网络中需要开启的小基站数目也会相应增加。此外，观察2个变量的变化趋势可知，用户达到率和小基站开启数目的变化过程并不是完全一致的，这是因为在本文提出的基于后决策状态的节能策略中，网络的当前决策不仅和当前的负载情况有关，且会受到未来网络负载的影响，故当宏基站的用户到达率有增大趋势时，网络会在宏基站的资源单元被完全占用之前调整小基站的开关策略以避免未来可能发生的宏基站资源短缺的情况。

图7 小基站开启数量和宏基站到达率关系图Fig.7 Relationship between the active numbersof SBSs and the arrive rates of MBS

图8给出了不同时延限制对网络总能耗的影响。图8中仿真了当宏基站时延限制分别为10，15，20时，网络总能耗的对比情况。观察图8可知，当把宏基站时延限制设置为10时，网络的总能耗值最高，而当把宏基站时延限制设置为20时，网络总能耗值最小。由此可知，更宽松的时延限制可带来更多的能量节约，但这是通过牺牲网络的服务质量实现的。因为网络可接受的时延限制越大，需要开启的小基站数量就越少，从而所需的能量消耗值就越少。因此，根据特定网络环境对时延和能耗的要求不同，可动态调整时延限制来满足不同网络的多样化需求。当网络环境对服务质量的要求更严格时，可设置较小的时延来满足网络需求，而当网络环境对能耗的要求更高时，可适当地放宽时延限制，以更低的能量消耗为相同数量的用户提供服务。

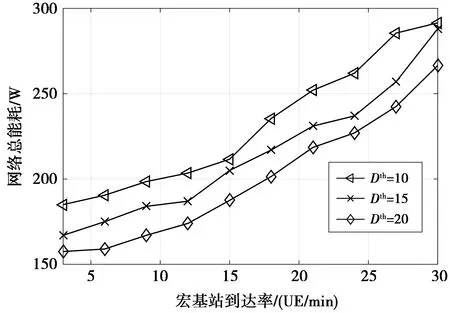
图8 时延限制和网络总能耗之间的关系Fig.8 Relationship between the delay constraintand the total energy consumption

7 结束语

因基站的能量消耗在整个网络能耗中占比最高，当网络中的负载水平较低时，关闭利用率较低的小基站是实现宏微网络节能的主要方式。为了根据动态变化的网络业务制定最优的小基站关断策略，本文将时延限制下长期平均能耗的最小化问题映射为CMDP，并引入后决策状态学习算法对模型进行求解。此外，本文还理论验证了后决策状态学习算法的收敛性。通过和Q学习以及实时动态规划这2种经典的增强学习算法对比可知，本文提出的后决策状态学习算法不仅收敛速度最快，性能最优，且可在满足时延限制的同时大幅度降低网络的能量消耗。

高效的资源分配方式也可达到节约网络能源消耗的目的，在未来的研究工作中，考虑采用后决策状态学习算法解决动态资源分配和基站关断策略联合优化问题已达到保证用户QoS的同时最小化网络能耗的目的。