网络切片中物理节点的分布式在线异常检测方法
王兆堃,陈前斌,唐 伦,王威丽
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆邮电大学 移动通信重点实验室,重庆 400065)
0 引 言
网络切片将一个物理网络划分为多个虚拟网络,每个虚拟网络都可以针对特定类型的应用程序或用户进行定制和优化,根据不断变化的用户需求将共享的物理网络资源动态高效地分配给各逻辑网络切片[1]。软件定义网络(software defined network, SDN)和网络功能虚拟化(network function virtualization, NFV)等技术,可以为运营商提供创建多个虚拟网络切片所需的可编程、灵活和模块化特性[2]。网络切片由虚拟网络功能(virtual network function, VNF)根据用户场景或业务模型进行组合,形成有序的VNF集合,即服务功能链(service function chain, SFC)。
网络切片增加了网络管理的复杂性,尤其是在大量网络切片的情况下,因此,对网络切片的自动化管理至关重要。实现网络切片的自动化管理,首先要能够迅速检测到网络切片中的异常。
文献[3]对比了基于机器学习的异常检测算法在NFV场景下的性能,证明了算法对VNF异常检测的有效性,但算法易受老化效应影响,模型不能及时更新会导致算法检测准确率出现明显的恶化。文献[4]通过分析服务功能链中相邻VNF各项观测数据的相关性,来推断SFC的运行状态。文献[5]提出了一种基于反馈告知机制的主动探测方法,通过探测包与VNF节点的告知信息判断SFC中异常发生的位置。文献[6]将基于多元线性回归和马氏距离的异常检测方法应用于NFV场景下的VNF异常检测,但该方法对特征指标的选择有较高要求,同时需要设定检测阈值。文献[7]将网络切片中底层物理节点运行状态细分为正常(normal)、退化(degradation)、恶化(deterioration)、中断(outage),通过引入迁移学习和隐马尔科夫模型,提出了迁移学习隐马尔可夫(transfer learning hidden Markova model, TLHMM)算法实现物理节点的快速异常检测。文献[8-10]在增量学习的基础上,通过对训练样本的动态更新,有效缓解了历史样本重复参与训练导致的训练时间增长。文献[11]在各子节点上独立运行聚类算法,最后在控制节点中合并子节点聚类簇群,实现网络异常检测。
现有网络切片与NFV场景下的异常检测研究主要有以下问题:①现有研究多关注VNF的部署和迁移问题,部分研究针对VNF异常检测问题。网络切片底层物理节点的异常会影响其上部署的多个网络切片的运行状态,但很少有研究针对底层物理节点实施异常检测;②部分研究在网络中引入了额外的通信开销,占用了宝贵的带宽资源,带来不必要的时间成本。
此外,机器学习类异常检测方法常采取的离线或增量学习方式,与VNF的灵活性、可调整性冲突,检测模型易受老化效应影响,同时也无法完全解决数据集增大带来的计算开销上涨;现有分布式异常检测方法在一定程度上避免了原始观测数据在网络中的传输,但其分布式节点独立完成训练,无法在训练阶段有效利用网络中其余节点的观测数据。
针对以上问题,本文提出了一种基于支持向量数据描述(support vector data description, SVDD)的分布式在线网络切片中物理节点异常检测方法,主要贡献如下:①提出了一种基于SVDD的网络切片中集中式离线物理节点异常检测模型;②为了解决VNF观测信息共享面临的技术保密难题和通信开销问题,提出一种分布式的物理节点异常检测模型,利用随机近似函数解决了核函数计算问题;③采用随机梯度下降(stochastic gradient descent, SGD)提出了一种分布式在线物理节点异常检测算法,在线的算法机制保证了模型的动态更新,同时有效地减轻了网络中异常数据导致的算法检测准确率下降。
1 系统模型
1.1 网络模型
假设底层物理网络由M个相互联通的物理节点组成,网络中映射到物理节点m上的虚拟网络功能共有N个,如图1。网络切片管理器根据不同业务的特定需求定制网络切片实例,每个网络切片实例都包含一组有序的VNF,这些VNF经由网络切片管理与编排器部署在同一个底层基础设施上,提供多样化的服务。基础设施管理模块负责管理网络切片部署所需的底层物理资源。

图1 网络切片部署场景Fig.1 Network slice deployment scenario
网络切片是一个共享的架构,不同的厂商可以同时在共享的物理网络上提供差异化的服务,出于技术保密和安全保护等原因,不同服务厂商间不愿共享彼此信息。部署于同一物理节点上的分属不同网络切片的VNF中各自蕴含着与所在物理节点运行状态相关的观测信息,但各VNF可能分属不同的服务厂商,这使得VNF观测信息共享面临困难。
网络切片按需定制、实施部署、动态保障的特性赋予了网络更多的灵活性,但其依托于虚拟化网络功能的架构也给网络带来了更多的安全挑战。3GPP等国际化标准组织针对网络切片的安全威胁、安全特性和解决方案展开了标准化研究。参考文献[12]指出,切片间的通信安全要求对网络中切片接口和通信进行保护,以加密隧道的方式保证切片与外部网络的通信安全。
切片间通过加密隧道的方式共享VNF观测信息会导致通信开销增大,同时也给网络切片运营商的技术保密带来挑战。因此,利用VNF观测信息检测物理节点异常的同时,必须保证观测数据在切片内本地处理,从而化解网络切片运营商的信息泄露担忧,降低切片间通信开销,减小切片间信息共享带来的安全威胁。
各网络切片管理器采集本切片内虚拟网络功能的观测数据,p时刻对物理节点m的观测数据为sp=(x1p,x2p,…,xnP)T,其中,xnP为部署在物理节点m上的VNFn在p时刻的观测数据向量,由流速率、排队时延、处理时延、协议类型等组成,分布式存储于各个网络切片管理器上。
为了在切片内本地化处理观测信息的同时,利用VNF观测数据,本文提出了一种分布式的网络切片中物理节点异常检测方法,将物理节点异常检测模型分布式部署在各网络切片中,从而解决VNF观测信息共享面临的难题,实现底层物理节点异常检测。
1.2 基于SVDD的分布式在线物理节点异常检测模型
传统移动通信网络相比,网络切片将底层物理网络划分为多个互相隔离的虚拟网络。每个网络切片逻辑上都是一个独立的端到端网络,由一组有序排列的VNF组成,可以在共享的底层物理网络上满足业务多样化需求[13]。与此同时,底层网络中单个物理节点的异常可能导致多个网络切片的性能下降。为了满足网络切片的高性能需求,快速发现底层网络中物理节点的异常具有重要的意义。
异常检测是数据挖掘领域的一个重要分支,传统的异常检测采用基于统计的检测方法,一般需要假设数据的分布模型,而基于机器学习的异常检测方法通过学习历史数据,生成代表正常或异常的行为模型。基于机器学习的异常检测方法也分为有监督和无监督2种:①有监督方法采用带有正常和异常标签的训练数据构建检测模型;②无监督检测方法则直接利用无标签的训练数据构建模型。在某些领域,由于异常数据样本获取难度大,且人工标记数据费时费力,为了充分利用目标系统运行时采集的无标签数据,单分类支持向量机得到了广泛的研究。
SVDD[14]是一种单分类支持向量机,该模型仅考虑正常类样本,通过将数据点从输入数据空间映射到高维特征空间,找到一个覆盖特征空间中大多数映射数据点的最小超球面,包含在超球面内的数据点为正常点,而超球面外的数据点则为异常点。
SVDD对无标签和样本不平衡数据有着良好的处理能力,网络切片在运行过程中会不断产生未标记的观测数据,并且,由于网络基本运行在正常状态,其产生的异常数据远远少于正常数据。本文采用SVDD对网络切片中物理节点异常检测问题建模,可以直接利用网络运行时产生的未标记观测数据实现物理节点异常检测。假设网络中收集到的数据均来自对网络切片正常运行状态的观测,对上述网络模型所给定的数据集S=(s1,s2,…,sP),构造凸二次规划问题
s.t. ‖φ(sp)-a‖2≤R2+ξp,
ξp≥0,p=1,2,…,P
(1)
(1)式中:φ(·)为将原始数据映射到高维特征空间的映射函数;a和R分别是特征空间中所得超球面的球心和半径;ξp是减少离群值影响的松弛变量;C为平衡超球面大小与错判数据点个数的惩罚参数。
对(1)式引入拉格朗日乘子βp≥0和ηp≥0构造如下拉格朗日函数
(2)
对(2)式关于变量a,R,ξ分别求偏导并置0
(3)
(4)
0≤βi≤C
(5)
φ(·)是形式未知的映射函数,通过引入核函数k(x,y)=〈φ(x),φ(y)〉求解,一般采用常见的高斯核函数k(x,y)=〈φ(x),φ(y)〉=exp[-‖x-y‖2/σ2],其中,σ是核宽度。
将(3)式、(4)式代入(2)式,求解对偶规划问题,可以得到判别函数
g(sp)=‖φ(sp)-a‖2-R2
(6)
当g(sp)<0时,观测数据处于超球面内,物理节点对应的时刻处于正常运行状态,反之则为异常。
(1)式对应的异常检测模型为集中式模型,需要在单个节点集中处理所有观测数据,无法满足VNF观测数据在所属切片内分布式处理的原则,为了满足这一原则,本文将上述优化目标分布式化。
同一物理节点上部署的各VNF可能分属不同网络切片,切片间安全和隔离需求使得VNF观测信息共享面临着巨大困难。为了解决这一问题,我们分布式化异常检测模型,在各切片内分布式处理观测数据,避免切片间VNF观测信息共享带来的巨大切片间通信开销和安全、隐私风险,实现物理节点异常检测。

C2:ξnp≥0,p=1,2,…,P
C3:an=am,Rn=Rm,n,m=1,2,…,N
(7)
(7)式中:xnp为p时刻VNFn的观测数据;N为映射到当前物理节点上的VNF数量,在(7)式中作为缩放变量。C1和C2为SVDD模型约束条件,约束条件C3保证各VNF对应局部参数最终收敛到相同的值。
由约束条件C3可知,对(11)式任意可行解都有a1=a2=…=aN,R1=R2=…=RN,满足这一条件时,(7)式等价于
s.t. ‖Φ(Xn)-a‖2≤R2+ξn,
ξn≥0n,n=1,2,…,N
(8)
(8)式中,Φ(Xn)=[φ(xn1),…,φ(xnp)]T。因为缩放变量N为常数,不难发现(8)式与(1)式等价,a*,R*也是(1)式的可行解,因此,我们提出的分布式优化目标(7)式也等价于(1)式。
与原优化目标相似,因为映射函数φ(·)是未知的,无法直接计算φ(xnp),通过引入高斯核函数的方式,转而求解k(xnp,xmp)。但在VNF观测数据分布式处理模式中,观测数据在各VNF对应的网络切片管理器中分布式存储,收集到的观测信息不在网络切片间传输,因此,无法通过高斯核函数计算k(xnp,xmp)=exp[-‖xnp-xmp‖2/σ2]。为解决此问题,本文参考文献[15]引入随机近似函数z(·)来近似φ(·),通过随机近似函数z(·):d→D将数据映射到随机特征空间,其中,d是输入空间的维度,D是随机特征空间的维度,D>d。通过引入随机近似函数,〈φ(xnp),φ(xmp)〉可由(9)式计算
〈φ(xnp),φ(xmp)〉≈z(xnp)Tz(xmp)
(9)
(9)式中,z(xnp)=[zω1(xnp),…,zωD(xnp)]T,随机近似函数z(·)是一个实值映射函数,其表达式
(10)
(10)式中:vi服从[0,2π]的均匀分布;ωi由高斯核函数的傅里叶变换p(ω)=(2π)-D/2e-[‖ω‖2/2]得到。
z(·)与映射函数φ(·)在再生希尔伯特空间中有相似的特性,与采用高斯核的φ(·)相似,z(·)同样可以将VNF观测数据xnp映射到一个圆心为0,半径为1的超球面中。参考文献[15]已经证明,D足够大时k(xnp,xmp)可以很好地被z(xnp)T·z(xmp)近似。
对(7)式采用随机近似函数后可得
C2:ξnp≥0,p=1,2,…,P
C3:an=am,Rn=Rm,n,m=1,…,N
(11)
经过随机近似映射函数映射后,(11)式中各参数的维度可能与(7)式中不同,为了避免再次引入复杂的变量定义,本文中仍以相同变量表示。在模型收敛到最优的全局共同参数a*和R*后,有判别函数
g(xnp)=‖φ(xnp)-a*‖2-(R*)2
(12)
对S=(s1,s2,…,sP)中任意xnp,g(xnp)<0表示该数据点正常,反之则为异常。
2 基于SVDD的分布式在线物理节点异常检测算法
网络切片中每个时刻都有新的VNF观测数据产生,如果存储所有数据进行离线的模型训练,不仅会占用大量的存储资源,离线训练的老化效应也会降低模型检测准确率;即使采取增量学习的训练方法,也需要存储历史观测数据,且历史观测数据重复参与模型训练。为了实现模型的及时更新,减小存储和计算资源占用,本文提出一个基于分布式SVDD的在线物理节点异常检测算法(distributed online support vector data description, DOSVDD)。
首先对(11)式引入朗格朗日乘子L和K,得到
s.t.ξnp≥0,n=1,2,…,N;p=1,2,…,P
(13)
(13)式中,l(an,Rn,ξnp;z(xnp))是损失函数,只有在保证损失函数可导的前提下,才能实现优化目标求解。为此,本文参考二次方平滑铰链损失函数给出l(an,Rn,ξnp;z(xnp))的定义
(14)
当(14)式满足(11)式中的约束条件C1时,l(an,Rn,ξnp;z(xnp))=0。将(14)式代入(13)式,得
(15)
s.t.ξnp≥0,n=1,2,…,N;p=1,2,…,P
SVDD模型训练一般采用增量学习方式,文献[10]提出一种基于支持向量合并的SVDD训练方法,以子数据集支持向量作为初始训练集,通过合并支持向量,限制训练过程中支持向量数量,加快了算法训练速度。但该方法仍然需要存储历史支持向量数据,且保留的支持向量样本重复参与新的训练过程。为了最大限度减小存储空间占用,动态更新模型参数,本文将(15)式转换为
Kmax(0,(‖z(xn(t))-an(t)‖2-
s.t.ξn(t)≥0,n=1,2,…,N
(16)
(16)式中,z(xn(t))=[zω1(xn(t)),…,zωD(xn(t))]T;t为在线学习的时隙;xn(t)表示VNFn在t时刻的观测数据,ξn(t)是xn(t)对应的松弛变量。
SGD是一种在机器学习和信号处理等多个领域广泛应用的优化方法,其每次迭代的计算复杂度低,不仅可以保留历史数据中的特征信息,也能够充分利用新的观测数据。对(16)式引入SGD可得
an(t+1)=an(t)-α1(t)∇anfn(t)
Rn(t+1)=Rn(t)-α2(t)∇Rnfn(t)
(17)

(17)式中,运算符(·)+表示对参数取正,以确保ξn(t)满足约束条件,an(t),Rn(t),ξn(t)分别为t时刻VNFn对应的参数an,Rn,ξn,αi(t)>0,i=1,2,3为SGD的学习速率,控制着参数更新的收敛速度,∇anfn(t),∇Rnfn(t),∇ξnfn(t)是t时刻VNFn对应的局部参数an,Rn,ξn的梯度,由(18)式给出
(18)
图2是DOSVDD算法的框图,算法主要分为实时数据收集、分布式在线SVDD参数更新和实时异常决策3个模块,实时数据收集与分布式在线SVDD参数更新在网络切片管理器中完成,实时异常决策在物理节点管理模块中完成。物理节点管理模块根据分布式参数更新值 将决策变量等参数返回给各分布式参数更新模块,各分布式参数更新模块据此进行下一轮参数更新。算法第11步丢弃异常数据更新的参数,减小了异常数据点对模型参数更新的影响,切片网络正常运行产生的少量异常数据不会导致检测准确率下降,因此,本算法可以部署在切片网络中,通过无标签的VNF观测数据实现物理节点异常检测。

图2 DOSVDD框图Fig.2 Block diagram of DOSVDD
一般认为SVDD的时间复杂度为O(P3),其中,P为数据集大小,而本文提出的DOSVDD算法中运算部分主要涉及到核函数近似与模型的参数迭代,与数据集大小无关。在网络切片中,每一时刻T都不断产生新的观测数据,当P=T足够大时,DOSVDD的时间复杂度要小于SVDD。在存储空间占用方面,DOSVDD的存储空间占用仅与观测数据种类相关,由于SVDD中需要存储每个时刻上产生的观测数据,其复杂度为DOSVDD的T倍。
网络切片中基于SVDD的分布式在线物理节点异常检测算法如下。
初始化:初始化迭代次数T,随机近似维度D,以及各虚拟节点n的对应变量an(0),Rn(0),ξn(0)
1:fort=0,1,2,…,Tdo
2: forn=0,1,2,…,Ndo
3: 虚拟网络功能n产生新的观测数据xn(t),通过随机近似函数计算φ(xn(t))的随机近似z(xn(t))
4: 根据(18)式计算∇anfn(t),∇Rnfn(t),∇ξnfn(t)
5: 根据公式计算an(t),Rn(t),ξn(t)

7: 将结果传输到VNF所属物理基础设施管理模块
8: end for
10: 决策变量d(t)=1 表示物理节点在t时刻处于正常状态,将所有节点的an(t),Rn(t),ξn(t)传递给各虚拟网络功能对应的参数更新模块
11: elsed(t)=-1,物理节点状态异常,丢弃an(t),Rn(t),ξn(t),以参数an(t-1),Rn(t-1),ξn(t-1)继续t+1时刻参数更新
12: end if
13:end for
3 仿真与性能分析
为了验证算法性能,首先参考文献[7]在MATLAB平台中搭建一个简单的网络切片场景。网络中有10个物理节点和6条服务功能链。服务功能链对应3种类型的网络切片,假设增强型移动宽带(enhanced mobile broadband, EMBB)切片对应的SFC由6个VNF组成,超可靠低时延(ultra reliable low latency communication, URLLC)切片对应的SFC由5个VNF组成,海量机器类型通信(massive machine type communication, MMTC)切片对应的SFC由4个VNF组成。各类SFC的数据包大小和包到达率根据其自身的特征定义,随机的将SFC映射到底层基础设施上,每一时刻都可以获取VNF上的观测数据如处理速率、流速率、排队时延、处理时延等。仿真参数如表1。

表1 网络切片场景仿真参数Tab.1 Simulationparameters of network slice
本文提出的DOSVDD算法以切片网络中单个物理节点上各VNF的观测数据为输入,训练过程不需要标签数据,但为了有效验证算法性能,网络切片仿真生成的模拟数据是有标签的,每一时刻都有物理节点运行状态标签b(t)=±1。当故障率为0时,网络切片仿真数据中没有异常值,当故障率为0.1时,网络切片仿真数据中异常值的比例为1/10。
为了评估所提出算法的性能,本文使用3个指标:检测准确率(DA)、真阳率上(TPR)和伪阳率(FPR),其定义如下
(19)
(19)式中,TP,FP,TN,FN的定义如表2。
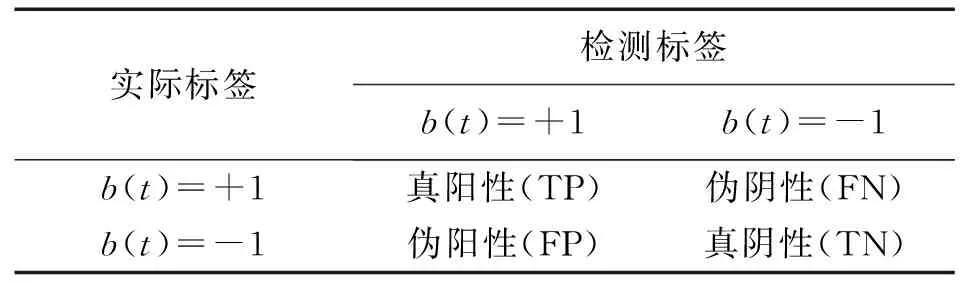
表2 性能评估参数定义Tab.2 Definition of performance parameter
完成网络切片场景搭建后,DOSVDD算法的拉格朗日乘子与惩罚参数的取值对比如图3,当L,C固定时,K的取值在0.3~0.7时算法性能最优,K值大于0.8后算法性能开始出现明显下降;当K,C固定时,L的取值在0.4~0.7性能最优,L大于0.8后算法性能也出现了下降,但下降程度较小,这是因为L控制各分布式参数的一致性,相对于控制超球面形成的K来说,其在一定范围内变化带来的影响相对较小。当L,K固定时,C的取值基本不对算法性能产生影响,因此,可以自由选取惩罚参数C的值。

图3 仿真参数对算法性能的影响Fig.3 Effect of simulation parameter on performance
综上,取拉格朗日乘子L=0.5,K=0.4,惩罚参数C=0.6,随机近似维度D=100,运行500次蒙特卡洛仿真,取均值作为算法输出。
图4评估了SGD学习速率αi(t)对算法性能的影响,其中,T为迭代次数,网络切片中故障率为0,即观测数据中无异常值。学习速率为算法收敛速度与收敛效果的折中,学习速率越大,算法收敛的速度越快,但较大的更新步长使得算法难以收敛到比较稳定的an(t),Rn(t),ξn(t)值;随着学习速率变小,收敛后的an(t),Rn(t),ξn(t)值波动较小,从而提升了算法检测准确率,但收敛速度变慢。取αi(t)=0.1/sqrt(T)时,初始阶段较大的学习速率可以有效加快算法收敛速度,随着迭代次数增多,学习速率逐渐减小,收敛后参数振动幅度更小更稳定,最终获得较好的检测准确率。

图4 SGD学习速率对算法性能的影响Fig.4 Effect of SGD learning rate on performance
图5对比了不同网络故障率情况下各算法的检测准确率,SVDD算法[16]采用集中式离线训练,OSVDD为集中式的在线SVDD算法。当模型训练数据中含有异常数据时,从图5中可以看出,SVDD和OSVDD的检测准确率受到了较大的影响,而DOSVDD算法则一定程度上避免了异常数据的影响,这验证了算法中步骤9-11的有效性。故障率达到0.2时DOSVDD才会出现较明显的性能下滑,但是网络在出现0.2的故障率时很难不被发现运行异常,这说明DOSVDD算法能够直接利用正常运行网络中收集到的无标签观测数据完成模型训练,少量的异常数据对算法性能影响不大。

图5 网络故障率对算法性能的影响Fig.5 Effect of network failure rate on performance
图6是几种异常检测算法检测准确率的对比。由图6可知,DOSVDD检测准确率与SVDD,OSVDD相当,因为分布式化的DOSVDD实现了与集中式SVDD相同的检测性能,并且DOSVDD具有更快的收敛速度,其分布式参数更新机制减小了切片间通信需求,避免了VNF原始观测数据共享带来的安全隐私问题。同时,DOSVDD算法有优于TLHMM算法检测准确率,因为TLHMM常用于解决多分类问题,其单分类性能弱于SVDD算法。

图6 不同算法检测准确率对比Fig.6 Comparisonon DA of different algorithm
图7表示DOSVDD算法的TPR相对于SVDD和OSVDD算法有轻微下降,这是算法的决策机制使得FN增大导致的,但异常检测算法更关注是否将故障节点误判为正常节点即FPR,而DOSVDD有着优于OSVDD的FPR。与SVDD相比,DOSVDD以可接受的TPR和FPR性能损失为代价,避免了切片间原始观测数据的传输,降低了检测模型的存储需求,缓解了算法更新过程中异常数据导致的算法性能恶化。

图7 不同算法TPR与FPR对比Fig.7 Comparisonon TPR and FPR of different algorithm
4 结束语
本文基于网络切片场景,针对网络切片物理节点的异常检测问题,建立了基于SVDD的异常检测模型并将其分布式化,提出了DOSVDD算法,避免了跨切片的VNF观测数据传输,实现VNF观测数据切片内处理,降低了检测节点存储性能需求,实现了模型的实时更新。仿真结果表明,算法可以在避免切片间传输原始VNF观测数据的同时,有效利用VNF观测数据实现网络切片中物理节点异常检测。

