CNLSTM模型预测城市积水
周小力,李 云,,王国胤,张 毅
(1.重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065;2.重庆邮电大学 计算智能重庆市重点实验室,重庆 400065;3.中电科技集团 重庆声光电有限公司,重庆 400060)
0 引 言
近年来,暴雨天气频发。巨大的降雨量容易导致城市内涝甚至洪灾,造成严重的经济财产损失。因此,精准且快速预测内涝积水从而为防灾减灾措施提供依据成为亟待解决的问题。
传感器技术与物联网技术的迅速发展使各地积水数据可以实时获取,并且能够为水位预测提供海量数据基础。因此,本文利用物联网平台中的传感器监测数据构建积水水位预测模型。
传感器监测数据具有时序性特点,传统的时间序列分析模型,如自回归滑动平均模型(autoregressive moving average, ARMA)[1]、差分自回归移动平均模型(auto regressive integrated moving average model, ARIMA)[2],灰色模型(grey model, GM)[3]等能够有效提取数据间的时序性及线性关系,但无法处理非线性关系。而神经网络可以通过有效的训练来识别数据间复杂的非线性关系,因而被广泛应用于各个领域,如降雨径流预报,水位预测等。A.Hamzic等[4]使用非线性自回归神经网络与前馈反向传播神经网络对湖泊水位进行预测,得到了较好的预测结果;J.Zhang等[5]使用灰色径向基神经网络(radial basis function neural network, RBF)构建水文预报系统,结果表明,模型拥有较好的精度和稳定性,验证了神经网络在预测中的可靠性;邵月红等[6]通过对比Elman动态神经网络和水文模型分析河流日径流量的情况,证明Elman动态神经网络可以更好地模拟日径流量,预报结果更为准确;张梦等[7]利用粒子群优化算法优化回声状态网络的超参数并将优化后的网络用于预测积水,与BP神经网络相比,得到了更精确的预测结果,验证了递归神经网络在积水预测方面的优越性。
虽然传统递归神经网络(recursive neural network, RNN)在水文时间序列预测领域取得了一定成果,但存在梯度消失或爆炸的问题,容易导致预测效果不理想。长短时记忆网络(long short-term memory, LSTM)是RNN的一种变体,其在很大程度上改进了对长期依赖性问题的处理能力,能够很好地处理与时间相关的数据。因此,LSTM被广泛应用于时间序列预测中[8-10],但是这种方法无法提取多变量数据之间的空间特征关系。卷积神经网络(convolutional neural network, CNN)是一种拥有强大空间数据处理能力的网络,已被广泛应用于图像识别领域[11-12],而将其用于多变量积水数据间的空间特征提取也是合理的,CNN能够通过卷积核自动提取原始数据中的局部特征,从而得到具有空间相关性的特征向量,组合模型理论上来说能够弥补单一模型的不足,拥有比单一模型更加优越的性能。冯钧等[13]提出了一种LSTM-BP组合模型进行水文预报,结果表明,此模型的预报结果优于单一模型,验证了组合预测模型的可行性及优越性。
因此,本文提出了一种基于神经网络的组合的时序预测模型(CNLSTM)来模拟复杂的积水动态过程,它同时拥有CNN和LSTM的优点,能够同时捕获多变量积水数据间的时空特征。具体而言,首先使用CNN卷积层作为特征提取的基础层;CNN通过共享局部权值降低网络的复杂度,构建出具有高级空间特征的特征向量;然后利用LSTM模拟当前积水状态和历史输入之间的关系,并根据时间序列数据中包含的特征对未来积水水位做出预测。
1 物联网中的积水监测
为了有效监测积水状态,本文利用物联网平台实时获取积水相关的传感器数据。物联网平台架构如图1,共分为4层:感知层,网络层,机器学习层和应用层。感知层包含了多种传感器,如水位传感器,流量传感器,雨量计等感知水位和排水情况,感知数据通过网关实时传输到网络层,经过路由寻址最终被送入到机器学习层,数据在此层能够得到有效的处理分析,最终得到的积水水位预测结果将会在应用层中展示。本文提出的CNLSTM积水预测模型是一种基于人工智能和大数据的先进算法,通过处理多变量积水数据对未来积水水位进行准确预测。详细的模型架构将在以下章节中介绍。

图1 物联网体系架构Fig.1 Internet of things architecture
2 建模原理
2.1 CNN基本原理
CNN在处理二维图像方面取得了巨大成功,而将这一理念应用于处理一维数据也并不困难[14]。本文采用一维卷积来捕捉积水数据之间的空间特征,可用公式表示为
hk=σcnn(wcnn⊙xk+bcnn)
(1)
(1)式中:⊙表示输入的一维积水特征量xk和过滤器权重wcnn之间进行逐元素相乘;bcnn表示偏差参数;σcnn是激活函数。
为了捕获不同的特征,在一个卷积层中采用了几个相同大小的过滤器,即多个卷积核。输入信号与每个过滤器进行卷积运算,然后将结果堆叠在一起作为输出。以卷积层中有2个卷积核为例,如图2,卷积操作被可视化为尺寸为卷积核大小的滑动窗口,沿着输入的序列以一定步幅移动。滑动窗口在图2中用红框表示。在过滤器1中,蓝线表示第1次卷积,绿线表示滑动窗口以步幅1前进了一个单位后,进行的第2次卷积。假设过滤器1的尺寸为4,权值为(1,-1,0,1),在不考虑偏差的情况下,第1个输出值为3×1+4×(-1)+1×0+2×1=1;第2个输出值为4×1+1×(-1)+2×0+2×1=5。输入序列以相同的方式与第2个过滤器进行卷积运算,输出13,11两值组成的向量,最后,将2个卷积核的运算结果组合成长度为4的向量(1,5,13,11)输出。由于积水相关的特征变量空间维数有限,因此不使用池化层。

图2 一维卷积层机制Fig.2 One-dimensional convolution layer mechanism
2.2 LSTM基本原理
LSTM是RNN最热门的变体之一。它通过门结构改善了梯度消失的问题。LSTM单元中包含3种类型的门:①输入门,它可以自适应的分配比例到单元存储器中;②遗忘门,主要表征给定输入的单元存储器的遗忘率;③输出门,主要控制单元存储器以影响节点输出。
假设输入序列为(x1,x2,…,xn),隐藏层输出序列为(h1,h2,…,hn),那么在t时刻,记忆细胞的输入输出结构表示为
it=σ(whiht-1+wxixt+bi)
(2)
ft=σ(whfht-1+wxfxt+bf)
(3)
ct=ft⊙ci-1+it⊙tanh(whcht-1+wxcxt+bc)
(4)
ot=σ(whoht-1+wxoxt+bo)
(5)
ht=ot⊙tanh(ct)
(6)
(2)—(6)式中:it为输入门输入;ct为细胞状态更新;ot为输出门输出;ht为隐藏层输出;σ为Sigmoid激活函数;whi,whf,whc,who为前一时刻LSTM细胞输出量对应的权重参数;wxi,wxf,wxc,wxo为输入量对应的权重参数;bi,bf,bc,bo为各部分的偏置值。可以通过梯度下降法迭代更新,直到模型收敛,从而确定最终模型的权重参数。
3 模型框架
积水状态具有空间和时间2种特征。空间特征表征不同传感器数据之间的相互关系,时间特征表征当前积水水位与过去输入之间的相关性。为了兼顾积水数据的2种特征,本文建立了一种组合的CNLSTM网络,用于准确预测积水水位。CNLSTM由2部分组成:①CNN,用于提取特征量数据之间的空间特征;②LSTM,用于预测未来的积水水位。
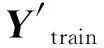

图3 CNLSTM预测模型结构图Fig.3 CNLSTM combined model structure figure
3.1 数据清洗
由于积水相关数据由传感器采集得来,而传感器容易受到温度、电压等环境因素的影响而发生漂移,从而造成数据缺失或异常等现象。因此,首先需要对收集到的传感器数据进行清洗。
本文使用文献[15]的方法对数据进行清洗。首先结合滑动窗口和莱茵达法剔除异常数据;然后运用自回归方法对缺失及剔除的异常数据进行填补。整个过程可描述如下。
假设某一传感器采集的数据为x1,x2,x3,…,x4,对于异常数据,可用以下步骤进行判断
(7)
(8)
(9)
由于当前积水相关的多变量数据与历史数据之间存在依赖关系,t时刻的数据xt依赖于前面时刻的值,因此,可用自回归模型对缺失数据进行填补,xt的自回归模型可表示为
xt=w1xt-1+w2xt-2+…+wpxt-p+εt
(10)
(10)式中:xt为t时刻的值;w1,w2,…,wp为各历史分量的权值;εt为服从标准正态分布的白噪声。将xt视为因变量,xt-1,xt-2,…,xt-p为自变量,可用最小二乘法得出w1,w2,…,wp的估计值。从而求得xt的值,对数据进行填补。
3.2 数据标准化
由于多变量传感器数据在单位量纲及数量级上存在较大差异,容易导致神经网络难以收敛,增大模型的训练难度,因此,需要对数据进行标准化处理。本文采用Min-max标准化方法。
(11)
(11)式中:x*为某积水因子标准化后的数据;x为某一类积水因子的原始数据;xmax为某一类积水因子的最大值;xmin为某一类积水因子的最小值。
3.3 模型训练
根据所提网络模型的结构,网络训练步骤如下。
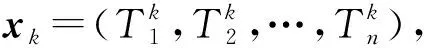
X=(x1,x2,…,xn)
(12)
步骤2划分训练集和测试集
Xtr=(x1,x2,…,xm)
(13)
Xte=(xm+1,xm+2,…,xn)
(14)
(13)—(14)式中,Xtr和Xte分别表示经清洗和标准化处理后的训练集和测试集数据,将数据集的前一部分设置为训练集,后一部分设置为测试集。满足约束条件m 步骤3处理数据为适合模型训练的时间序列。设置时间步长为L来分割Xtr,分割后数据可表示为 Xtrain={(x1,x2,…,xL),(x2,x3,…,xL+1),…, (xm-L,xm-L+1,…,xm-1)} (15) Ytrain=(xL+1,xL+2,…,xm) (16) (15)—(16)式中:Xtrain为模型的输入向量集,被送入CNN隐含层中;Ytrain为模型预测值对应的实际值向量。通过前L个时间步长的数据,预测L+1时刻的积水水位。 步骤4模型输出。数据经CNN隐含层处理后送入到LSTM隐含层中。最后,经过LSTM中的全连接层作为回归层输出,从而得到积水水位预测值。 (17) 以海口某地积水情况的监测数据来进行建模预测。本文通过采集2017年到2018年共1年的积水点水位数据以及积水点附近的泵站、河道、闸门、排水道水流速度、雨量数据来研究积水状态。这些数据来源于各自的监测传感器。数据为每小时采集一次。 其中,积水水位用yd表示;泵站状态由2个水位传感器联合监控,实时上报进水侧水位pi与出水侧水位po数据;河道状态包括河流的水位与流量情况,分别用rl,rf表示;闸门开合度由g表示;水流速度和降雨量分别由wv和rn表示。数据经过清洗和标准化处理后送入预测模型中,t时刻的输入量可表示为 (18) 网络输出为水位预测值,表示为 (19) 本文采用keras神经网络学习框架对模型进行搭建,使用Python语言实现建模与计算。根据多次试验,设置卷积层具有2个长度为3的过滤器最为合理,然后设置LSTM隐藏层为1层,其中具有100个隐藏节点。最后设置一个具有1个节点的全连接层作为回归层。将样本划分为2部分,选取前70%的数据作为训练集来训练模型,后30%的数据作为测试集来验证最终模型的预测准确度。模型的输入层输入积水向量,输出层输出预测结果。在训练期间,训练的批量大小batch size设置为80,epoch设置为60。所有网络参数都是随机初始化的。在训练过程中使用0.5的截止率。优化器使用Adam优化器,它根据损失函数的梯度选择网络权重和偏差。初始学习率设置为0.01。模型中具体的参数设置如表1。 表1 CNLSTM模型参数设置Tab.1 CNLSTM model parameter settings 训练过程的损失函数采用预测积水水位与实际积水水位之间的均方误差(mean-square error, MSE)。损失函数表示为 (20) 在测试过程中,使用均方根误差(root mean squared error,RMSE)和平均绝对误差(mean absolute error,MAE)评估网络的性能,分别表示为 (21) (22) 本文所提模型预测结果如图4。图4a中显示了预测值与实测值的对比效果,其中包含了300组数据。可以看出,预测水位值与实测水位值曲线高度拟合。观察图4b,模型中超过90%的采样点的预测偏差在0.5%以内,最大偏差也没有超过1%。预测模型的收敛情况见图4c,loss在快速下降到0.02之后缓慢下降,最后几乎稳定保持在0.013左右,达到收敛。根据训练集和测试集的损失函数收敛情况,可以发现所提模型拥有很好的准确性和泛化性,没有出现高偏差和高方差的情况,即没有欠拟合和过拟合。 图4 CNLSTM预测结果Fig.4 CNLSTM prediction result 将所提网络的性能与CNN,BP网络和文献[10]中使用的LSTM网络进行比较。所有网络的epoch都设为60。图5显示了4种网络的预测结果与实际水位。可以看出,BP网络的误差最大。与LSTM网络和所提网络相比,CNN网络的预测结果产生了较大波动。相比之下,LSTM网络和所提网络的积水估计更加准确。图6显示了所提网络模型与LSTM网络的估计误差,其中,所提网络的估计误差基本保持在0.5%左右,而LSTM网络的最大估计误差几乎达到了2%。从整体来看,LSTM网络的误差大于所提网络的误差。因此,相比于LSTM网络,所提网络的预测结果更好一些。由此可见,本文所提网络优于BP,CNN和LSTM网络。 图5 预测结果对比Fig.5 Comparison of prediction results 图6 估计偏差对比Fig.6 Estimated deviation comparison 表2中列出了更多的统计结果,可以看出,相较于BP,CNN和LSTM,所提网络的RMSE和MAE值均最小,预测精度最高。 表2 预测精度表Tab.2 Prediction accuracy table mm 本文提出了一种组合的CNLSTM时序预测模型来预测积水点水位。首先利用CNN网络提取输入量之间的空间特征,然后将经过CNN处理后的数据送入LSTM网络中,利用LSTM网络提取数据之间的时间特征,从而预测未来时刻的积水水位。利用物联网平台收集积水点传感器数据,并评估CNLSTM的性能。实验结果表明,所提网络能够成功提取积水水位与输入变量之间的非线性关系。与CNN,LSTM和BP网络相比,所提网络呈现更平滑的预测结果和更好的精度。准确预测积水趋势能够为城市积水情况的改善及预防措施提供依据,减少因积水造成的财产损失。4 结果分析
4.1 数据收集
4.2 参数设置

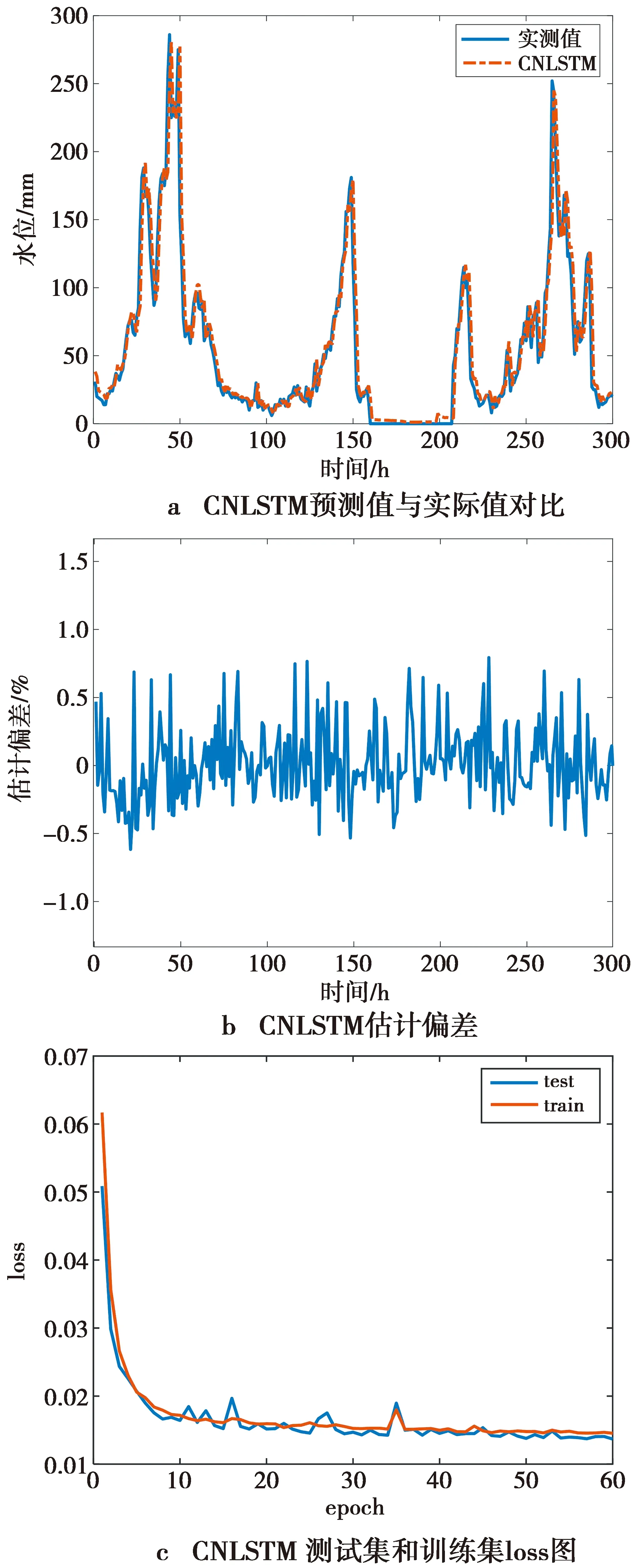
4.3 预测结果
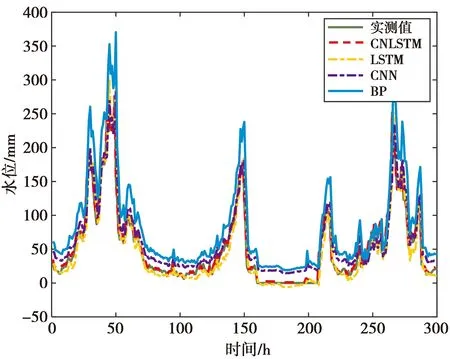
4.4 模型对比分析


5 结束语

