某高层住宅大震作用下结构整体性能评价

洪承禹 （安徽省施工图审查有限公司，安徽 合肥 230000）

为达到建筑物受罕遇地震影响时，不发生倒塌或严重破坏的抗震设计目标，通常采用以抗震性能为基准的设计思想和以位移为基准的设计方法。

基于结构性能的抗震设计方法是使被设计的建筑物在使用期间满足各种预定功能或性能目标要求，使抗震设计从宏观定性的目标向具体量化的多重目标过渡，具体来说就是对结构进行复杂的非线性地震反应分析，通过对结构各构件及结构整体性能的研究，得到结构系统在地震下的反应，以证明结构可以达到既定的性能目标。

结构丧失稳定以致倒塌一般是由于重力作用在有过大侧向变形的结构上所引起的，这种效应被广泛称为“P-Δ”效应。因而达到防倒塌设计目标的中心思想是限制结构的最大总弹塑性变形在规定的限值以内。

1 工程概况

某6度区高层住宅地下3层，地上60层，剪力墙结构，建筑高度约190m，抗震设防类别为标准设防类，标准层平面见图1。根据本工程结构特点和超限类型并征询业主的意见，按照《高层建筑混凝土结构技术规程》第3.11节，本工程抗震性能目标选为C；各地震工况下的性能水准依次为1、3、4。

图1 标准层平面图

本文对该工程进行罕遇地震作用下的动力弹塑性时程分析，研究结构在大震作用下的基底剪力、顶点位移、层间位移角等综合指标，评价结构在大震作用下的力学性能。

2 分析方法

采用有限元软件Midas Building对本工程进行动力弹塑性时程分析，考虑以下因素。

①几何非线性：结构的动力平衡方程建立在结构变形后的几何状态上，可以精地考虑“P-Δ”效应、非线性屈曲效应、大变形效应等非线性影响因素。

②材料非线性：直接在材料应力-应变本构关系的水平上进行模拟，真实地反映了材料在反复地震作用下的受力与损伤情况。

③采用直接积分，可以准确模拟结构的破坏情况直至倒塌形态。

3 非线性地震反应分析结构模型[4]

3.1 剪力墙模拟

剪力墙采用的是基于材料本构的纤维束模型，用不同的纤维束分别模拟混凝土和钢筋材料。

3.2 钢筋/型钢混凝土梁模拟

钢筋/型钢混凝土梁采用的是基于构件的非线性模型，其塑性损伤采用集中的塑性铰来模拟，塑性铰采用的是PM铰。

3.3 阻尼比取值

结构阻尼采用瑞雷阻尼，选择T=0.25T和，在5%的阻尼比下计算质量矩阵和刚度矩阵比例系数α和β的数值，随着地震波的输入，结构部分构件进入塑性状态，程序自动更新阻尼矩阵。

4 地震波选取

本工程选取了两条天然波及一条人工波。地面运动峰值加速度：125cm/s(主方向)；106.3cm/s(次方向)。地震波有效持续时间不小于5倍基本周期；地震波输入时间间隔0.02秒。大震弹性时程分析基底总剪力值与规范振型分解反应谱法计算基底总剪力值满足规范要求的多条地震波计算所得结构底部剪力的平均值不小于振型分解反应谱法计算结果的80%，单条地震波计算底部剪力不小于65%的要求。所选波基本满足规范要求的多组时程波计算的平均谱与振型分解反应谱法计算所用的规范谱相比在统计意义上相符的要求。

5 结构整体性能评价

5.1 基底剪力时程曲线

图2～图3为大震地震波（天然波1）作用下结构基底剪力时程(弹性时程和弹塑性时程对比)，本文仅列出天然波1作用主方向的基底剪力时程。

图2 天然波1X主方向基底剪力时程

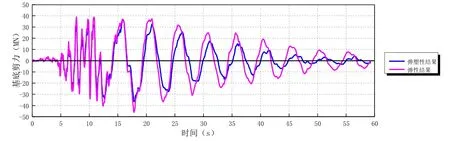
图3 天然波1Y主方向基底剪力时程

X方向和Y方向情况有所不同：①从结构的平面尺寸和构件布置可知，结构的X方向平面尺寸较长，但除个别几道长墙肢外，均为小墙肢，靠较多的框架梁和连梁等耗能构件连接而成形成抗侧力体系；Y向平面尺寸较短，但几乎均为长肢墙，耗能构件较少。②本工程X向风荷载下基底剪力、倾覆力矩和小震水准下计算结果基本相当，但是Y向为显著的风控，风荷载作用下基底剪力、倾覆力矩和中震水准下计算结果基本相当，因此在弹性计算时风荷载控制也使得Y方向结构的抗震承载力有较大的富余。③在地震波作用的初始数秒，结构仍然处于弹性阶段，弹性和弹塑性分析基底剪力基本吻合；随着时间的推移，地震作用的加大，输入能量逐步累积，结构也相继进入塑性，地震力也出现相应的偏差。X方向进入塑性更为明显，周期延长显著，Y方向弹塑性基底剪力和弹性基底剪力时程曲线趋势基本一致，数值差距不大，说明Y方向的抗侧刚度削弱不明显，Y方向的抗侧力构件(剪力墙和耗能构件)进入屈服阶段的数量较少。

5.2 顶点位移时程曲线

图4～图5为大震地震波（天然波1）作用下结构顶点位移时程(弹性时程和弹塑性时程对比)，本文仅列出天然波1作用主方向的顶点位移时程。可见，在地震波作用的初始数秒，结构仍然处于弹性阶段，弹性和弹塑性分析顶点位移基本吻合；随着时间的推移，地震作用的加大，输入能量逐步累积，结构也相继进入塑性，结构周期延长，顶点位移也出现相应的偏差。从各条波作用下顶点位移时程来看，结构仍然处于直立状态，满足大震不倒的要求。

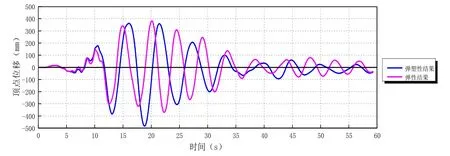
图4 天然波1X主方向顶点位移时程

图5 天然波1Y主方向顶点位移时程

5.3 最大层间位移角曲线

图6～图7分别为三组大震地震波作用下结构各楼层最大层间位移角曲线，本文仅列出地震波作用主方向的层间位移角。可见，各楼层层间位移角最大值均满足1/120的限值要求。

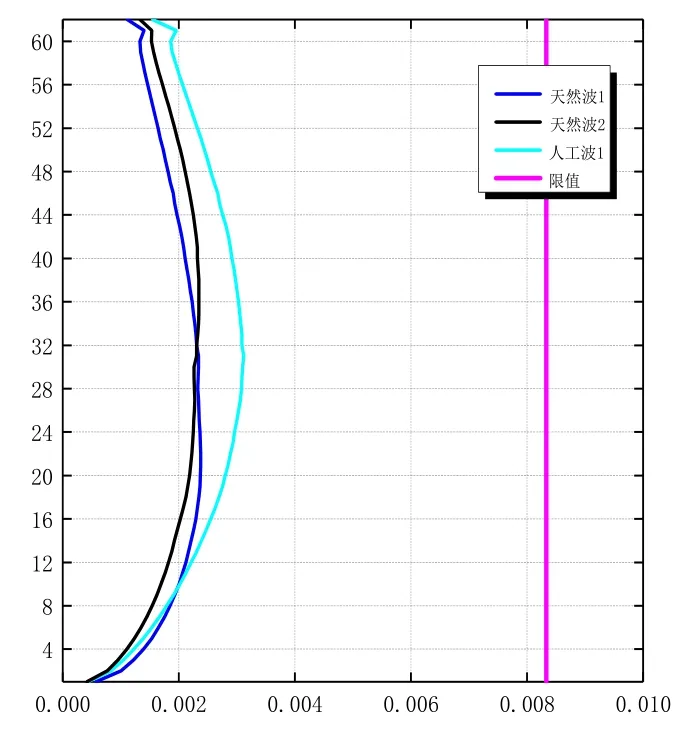
图6 X主方向层间位移角曲线

图7 Y主方向层间位移角曲线

5.4 结构屈服机制

由于计算分析的波较多，本文仅给出天然波1作用下结构屈服情况。从图7可以看出剪力墙均未进入屈服阶段，下面仅通过耗能构件塑性铰在不同时刻的开展情况直观了解结构的屈服机制。

图8～图14给出地震波作用不同时刻框架梁及连梁的塑性开展情况，由图可见：在5s时，部分框架梁及连梁出现塑性铰，但铰状态均为第1屈服状态，即混凝土开裂；在15s时，结构的中下部区域的耗能构件已经进入第2屈服状态，即梁内纵筋屈服，可有效参与耗能；在30s时，进入第2屈服状态的耗能构件数量进一步增多，在结构的上部区域也陆续出现塑性铰；30s之后新增的塑性铰数量不是太多(见图11)，最终时刻进入第2屈服状态的塑性铰数量约占64%。顶部框架柱并未出现塑性铰，剪力墙未进入屈服阶段。

图8 剪力墙受压应变等级

图9 5s时耗能构件整体屈服状态

图10 15s时耗能构件整体屈服状态

图11 30s时耗能构件整体屈服状态

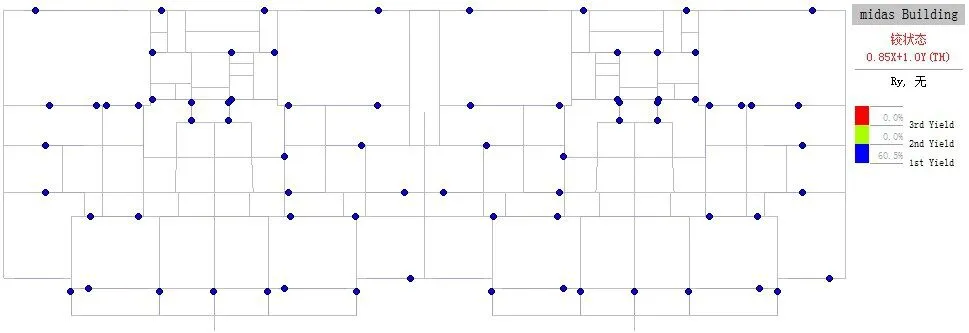
图12 20层框架梁及连梁（梁单元）5S时屈服状态

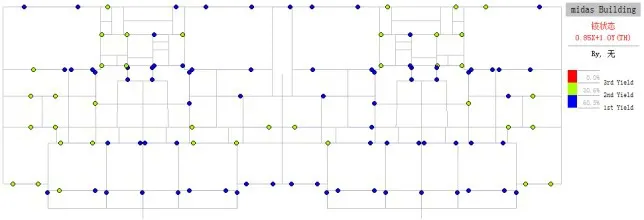
图13 20层框架梁及连梁（梁单元）15S时屈服状态

图14 20层框架梁及连梁（梁单元）30S时屈服状态

可见，连梁作为结构抗震第一道防线，在地震作用下能迅速进入损伤阶段，并在整个地震过程中保持耗能作用，有效保护了剪力墙肢免受破坏，结构有合理的屈服机制，有较好的耗能能力。

6 结语

通过大震动力弹塑性分析结果表明：结构体系在罕遇地震作用下整体变形(最大楼层层间位移角)小于规范最大值1/120的允许限值；结构体系拥有合理的屈服机制，有较好的耗能能力。可见，本工程结构构件在大震下均能达到预定的性能目标，满足大震不倒的设防要求。