采用分离变量法的载荷位置识别技术研究
张景 张方 姜金辉

摘要: 基于分离变量法提出了一种新的识别动载荷位置及时间历程的方法,以提高载荷定位的效率。根据结构系统参数建立响应与外部载荷之间的卷积关系式并离散化;采用分离变量法将载荷位置信息从脉冲响应函数矩阵中提取出来,根据响应信息选取合适的模态;利用正则化技术对载荷识别过程中的不适定问题进行求解;结合简支梁的仿真计算和实验测试对该载荷定位方法进行验证。研究结果表明,基于分离变量法的载荷识别方法能够准确地定位结构载荷位置并识别载荷时间历程,总体误差较小,相关性系数较大。相对于传统载荷位置识别算法,分离变量法减少矩阵求逆次数,提高了载荷定位的效率。
关键词: 载荷识别; 载荷定位; 载荷重构; 分离变量法; 模态截断法
中图分类号: TB123; O327 文献标志码: A 文章编号: 1004-4523(2021)03-0584-08
DOI:10.16385/j.cnki.issn.1004-4523.2021.03.016
引 言
载荷识别技术是一种在结构系统参数及响应已知的情况下,反向识别结构外部载荷的技术。
近年来,大量学者参与了载荷识别技术的研究,使得各种动载荷识别方法得到了快速发展。目前,关于动载荷识别方法的研究主要分为两大类:频域识别方法和时域识别方法。Bartlett 和Flannelly[1]于1979年首次将频域识别方法应用到了直升机桨毂力的识别。Hillary和Ewins[2]于1984年建立了较为系统的频域动载荷识别方法。1993年,Doyle[3]提出了一种小波模型,并利用谱分析法来识别作用于复合梁上的动载荷。频域载荷识别方法经过多年的研究已经较为成熟。在频域法中,需要利用傅里叶变换等类似的谐波变换将足够长的时域数据转换到频域下,这使得频域法的应用范围受到数据的长度限制。频域法对于识别频率成分较为简单的载荷具有很好的准确性,而对于频率成分比较复杂的载荷,例如冲击载荷来说并不适用,由此发展了时域载荷识别方法。Desanghere等[4]建立了时域动载荷识别方法,并首次利用模态坐标变换的方法来识别结构的外部动载荷。结构动载荷识别问题是一个逆问题,且在大多数情况下是病态的。针对这一情况,学者们提出了几种正则化方法来解决动载荷识别过程中的病态性问题。Jacquelin等[5]分别研究了Tikhonov正则化方法和截断奇异值分解法两种方法识别板上作用载荷的有效性。高伟等[6]采用范数拟合正则化方法识别载荷,并提出一种单调性检验方法用于最优正则化参数的选取。缪炳荣等[7]基于Green核函数方法建立动力学方程,通过混合正则化算法对不适定问题进行求解,并比较了不同正则化参数选取方法对识别结果的影响。由于载荷识别模型的建立需要依赖于测点的分布信息和载荷作用位置信息,因此,大部分研究都是在载荷作用位置已知的前提下进行的。但在实际工程中,载荷作用位置通常情况下是未知的。为了解决这一问题,Gaul和Hurlebaus[8]利用小波变换得到冲击波到达各个传感器的时间差,从而识别出冲击载荷的作用位置。Alajlouni等[9]利用波在传递过程中存在衰减这一原理来识别板上的冲击载荷位置。顾慧芝等[10]采用了一种新的载荷识别方法,即等效点动标定法来识别在作用位置未知情况下的动载荷。周晚林等[11]采用BP神经网络与有限元逆分析相结合的方法来识别载荷的作用位置以及载荷的幅值大小。严刚和周丽[12]将响应计算值与实际测量值的差作为最小优化目标函数,从而将动载荷识别问题转化为参数优化问题,该方法能够识别出冲击载荷的作用位置并且近似地重建作用载荷的时间历程。祝德春等[13?14]建立了一种识别动载荷作用位置的方法,即最小判定系数法,該方法利用不同测点的响应在虚拟载荷作用位置处识别得到相应的当量动载荷,令其差值作为最小优化目标函数,通过识别最小优化参数来确定载荷作用位置。赵银燕等[15]基于奇异值分解和模态空间理论识别了梁上多点动载荷的位置和大小。文献[16?17]将载荷识别问题转化为约束优化问题,采用复合形法来定位载荷,并利用梯度投影法识别载荷时间历程。前面介绍的一些算法各有优点和缺点。在一些位置识别的算法中,对于每一个虚拟载荷位置,都需要进行两次矩阵求逆,当虚拟载荷作用位置较多时,要识别出真实的载荷作用位置就需要进行大量的矩阵求逆,这会消耗大量的计算时间。
本文提出一种基于分离变量法的载荷位置识别方法,该方法将载荷位置信息从脉冲响应函数矩阵中分离出来,使得整个位置识别过程中只需进行一次矩阵求逆,极大地缩短了计算时间。通过简支梁的仿真计算和实验测试,验证了该载荷定位方法的准确性和实用性。
1 动载荷识别的基本理论
对于一般的线性系统,外激励引起的系统响应等于时间区间上所有脉冲激发起的系统响应总和,即
式中 表示系统的单位脉冲响应函数。上式称作Duhamel积分或卷积积分。
对于一个自由度数为N的系统,假定载荷的作用位置为,则系统点的响应可由下式得到
式中 为在点作用单位脉冲载荷,系统点的单位脉冲响应函数。中包含了系统的响应点位置信息以及系统的加载点位置信息。
为了重构动载荷,通常将式(2)中的卷积积分离散化。对于初始条件为零的系统,设采样间隔为,采样点数为,时间刻度,则式(2)可以离散化为以下矩阵形式
对于一个载荷未知的系统,式(4)中的未知量只有载荷的加载位置以及载荷向量。当载荷的加载位置确定以后,只需要对式(4)进行求逆,就可以得到载荷的时间历程。为了定位该载荷的加载位置,至少需要两个测量点的响应数据。
假设已知点1和点2的响应,指定系统中任一点作为可能的载荷激励点,将该点称之为虚拟载荷位置,分别利用点1和点2的响应对式(4)进行求逆,得到两个当量动载荷和。理论上,若此时的虚拟载荷位置恰好与真实的载荷作用位置相一致,那么求得的两个当量动载荷应该相等。但由于响应测量过程中的误差难以避免,因此求得的两组当量动载荷可能存在较小的差异。此时,可以将识别动载荷位置的问题转化为最小优化问题,引入优化参数表示当量动载荷和的差值,则优化参数为位置变量的函数。当位置变量恰好为真实的载荷作用位置时,优化参数取得最小值。因此,动载荷位置识别就转化为寻找优化参数的最小值所对应的位置变量。的表达式如下
通过寻找优化参数的最小值来确定真实的载荷加载位置。在此过程中,每假定一次虚拟载荷位置,就需要进行两次矩阵求逆。若系统的自由度数为N,为了确定动载荷的位置,则通常需要进行2N次矩阵求逆。由于矩阵求逆过程较为耗时,因此当N较大时,整个识别过程需要耗费大量的计算时间,这将给动载荷识别研究和实际工程应用带来极大的不便。
2 基于分离变量法的动载荷定位
为了提高动载荷位置识别的效率,提出一种基于分离变量法的动载荷位置识别方法,该方法将位置变量从脉冲响应函数矩阵中分离出来,以减少式(4)的求逆次数。
从式(10)可以看出,动载荷的位置信息包含在向量中,而矩阵中只含有系统的固有参数以及测点信息,因此当测点位置确定后,矩阵就可以确定下来。由于式(10)是一个欠定的方程组,所以无法通过该方程组直接得到未知向量的唯一解。为了确定向量的唯一解,这里采用模态截断法,通过响应分析选取对响应贡献较大的几阶模态,此外联合多个测点的响应数据。假设测点个数和选取的模态个数都为,可以得到以下方程组。
通过方程组(11)可以得到向量的唯一解,然后利用向量的各个分量可以得到个载荷向量
而对于真实的载荷作用位置,个载荷向量应该近似相等,因此,引入优化参数
将载荷定位问题转化为最小参数优化问题。当优化参数取得最小值时,所对应的即为真实载荷位置。
在此载荷位置识别方法中,只进行了一次矩阵求逆的步骤,这极大地缩短了识别计算时间。通常情况下,对于一个维的矩阵,在采用初等行变换法对其进行求逆的过程中,需要进行次加法运算和次乘法运算。而对维的矩阵进行求逆,需要进行次加法运算和次乘法运算。在传统载荷位置识别方法的过程中需要进行2N次维矩阵的求逆,而基于分离变量法的载荷位置识别方法,只需要进行一次维矩阵的求逆。由于加法运算比乘法运算时间短,仅以乘法运算来比较两种算法的时间,下式为两种算法运算时间的比值
若取,则当系统的自由度数N和模态个数分别取不同值时,两种算法的时间比值如表1所示。
通过以上比值可以看出,当系统的自由度数N较大以及选取的模态数较少时,基于分离变量法的载荷位置识别方法将极大地缩短运算时间。
在实际应用中,由于测量误差以及模态截断的影响,直接对式(11)求逆可能不会得到较为理想的结果,因此可以利用正则化算法来减小误差的影响,以确保结果的准确性。此外,由于模态截断的影响,通过此方法得到的载荷时间历程可能并不十分精确。因此,在识别得到载荷位置之后,可以利用式(4)进行载荷时间历程的识别。
3 仿真验证
以两端简支的梁模型为例,在其上作用集中载荷,通过有限元仿真计算,分别研究了分离变量法对于简谐载荷和冲击载荷位置识别的有效性。其中,简支梁的长度 m,宽 cm,高 cm,泊松比,弹性模量 GPa,密度 kg/m3。将简支梁的有限单元模型划分为1000个单元,共1001个节点。
3.1 简谐载荷的识别
在距离简支梁一端0.31 m处施加一个正弦载荷,该正弦载荷的频率为60 Hz,幅值为100 N,如图1所示。
距离一端 m和 m两点为测量点,测点的响应通过仿真计算得到,并加入5%的高斯白噪声(最大响应值的5%)。测点的响应如图2和3所示。
为了识别简谐载荷的作用位置,选择截取简支梁的前两阶模态。在识别计算的过程中,为了减小噪声误差及模態截断对识别计算结果的影响,采用了Tikhonov正则化方法,并通过L曲线法来确定正则化参数的大小。为确定真实的载荷加载位置,分别假设除去两个端点外的999个节点为虚拟载荷位置,计算相应的优化函数值。简支梁各个位置的优化函数值如图4所示,其中优化函数在0.311 m处取得最小值。因此识别出的简谐载荷加载位置为0.311 m,与真实载荷位置较为接近,可以认为识别结果较为准确。
在识别载荷过程中,计算得到的两个载荷向量和如图5所示。图5已经可以近似表示真实的载荷时间历程。此外,分别利用两个测点的响应,通过式(4)直接识别得到载荷向量,如图6所示。
识别载荷与真实载荷之间的相对误差及相关系数计算公式为:
式中 和分别表示识别载荷与真实载荷,为求平均值。
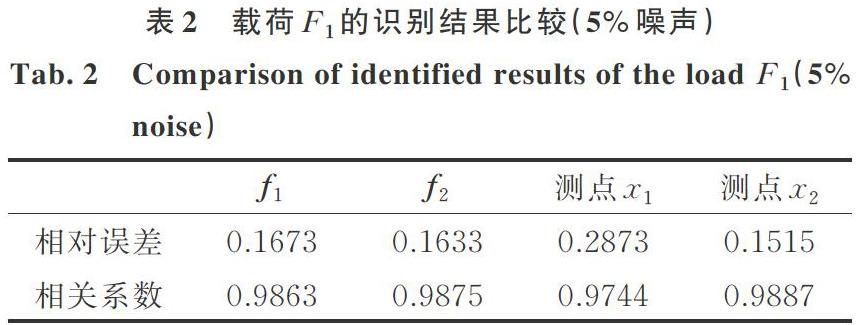
4组载荷向量与真实载荷向量的相对误差和相关系数如表2所示。可以看出4组载荷向量都有较高的精度,其中,通过测点的响应识别得到的载荷向量相关系数最高,误差最小,最为接近真实载荷,这是由于测点的响应幅值相对于测点的响应幅值较大,因此测点的响应信噪比较好。
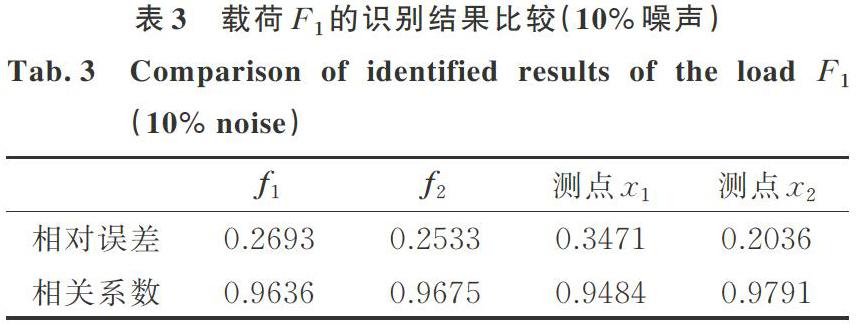
当响应中加入10%的高斯白噪声后,根据分离变量法识别得到的载荷加载位置为0.313 m,与真实载荷位置较为接近。另外识别得到的4组载荷向量与真实载荷向量的相对误差和相关系数如表3所示。可以看出,当响应中的噪声水平增加时,根据分离变量法识别得到的载荷位置以及载荷时间历程的误差会有一定的增大,但是与真实载荷依然较为接近。
3.2 冲击载荷的识别
本节对识别冲击载荷进行仿真验证,在距离梁一端0.28 m处加载一个冲击载荷,的真实载荷曲线如图7所示。同样以距离一端 m和 m两点为测量点,测点的响应通过仿真计算得到,并加入5%的高斯白噪声(最大响应值的5%)。
为了识别冲击载荷的作用位置,同样选择截取简支梁的前两阶模态。图8显示了简支梁上各位置的优化函数值,在图上显示出最小优化函数值对应的位置为0.283 m,与真实载荷加载位置0.28 m较为接近,满足识别精度要求。
此外,图9和10分别显示了由分离变量法和常规算法识别出的载荷曲线。4组识别得到的冲击载荷曲线的相对误差和相关系数如表4所示。由表4可以看出,利用测点响应采用常规算法得到的载荷曲线精度更高,同样,通过测点的响应识别得到的冲击载荷向量最为接近真实载荷。
同樣在响应中加入10%的高斯白噪声,根据分离变量法识别得到的冲击载荷加载位置为0.288 m,识别得到的载荷向量与真实载荷向量的相对误差和相关系数如表5所示。可以看出,根据分离变量法识别得到的载荷位置及载荷曲线较为接近真实载荷。
4 实验验证
为了进一步验证基于分离变量法的载荷定位方法的准确性以及工程实用性,利用一简支梁模型建立了动载荷识别实验,如图11所示。该梁长 m,宽 m,高 m,泊松比,弹性模量 GPa,密度 kg/m3。
通过有限元建模,将该简支梁模型均匀地划分为695个单元,共有696个节点。通过仿真计算得到该梁的前3阶固有频率,将其与实验测量得到的数据进行比较(如表6所示)。从表6可以看出,建立的有限单元模型与实际简支梁模型较为一致。
在梁上距离右端 m处利用力锤作用冲击载荷。通过传感器采集得到 m和 m两处的加速度响应信号,并通过两次积分得到两个测量点的位移响应数据。通过对位移响应信号进行FRF分析(如图12所示)。可以看出位移响应信号主要集中梁模型的在前两阶模态中,因此,选择截取前两阶模态来识别冲击载荷的作用位置。
通过分离变量法识别计算,得到冲击载荷的优化函数曲线(如图13所示)。从图中可以看出,识别的载荷位置为0.251 m处,与冲击载荷真实加载位置基本一致。详细的识别位置信息如表7所示。
对于简谐载荷的识别验证,在梁上距离右端 m处利用激振器施加一个频率为60 Hz的简谐载荷。测量点选择 m和 m两处,同样通过两次积分得到两个测量点的位移响应数据。截取前两阶模态,通过分离变量法识别计算的结果为0.148 m,与真实载荷加载位置基本吻合。简谐载荷的优化函数曲线如图14所示。详细的识别位置信息如表7所示。
从上述实验识别结果可以看出,冲击载荷位置和简谐载荷位置的识别结果都较为接近真实位置,因此认为该方法具有较高的准确性以及工程实用性。在确定载荷作用位置之后,为了更为准确地识别出载荷时间历程,可以直接利用式(4)来计算出载荷时间历程,为消除噪声误差及模态截断的影响,可以采用正则化算法来得到稳定的载荷曲线。
5 结 论
本文提出的基于分离变量法的动载荷位置识别方法,通过将载荷位置变量从脉冲响应函数矩阵中提取出来,并采用模态截断的方法来识别动载荷位置。在利用该方法识别计算的过程中,仅需进行一次矩阵求逆的运算,这极大地提高了动载荷位置识别的运算效率。仿真和实验的结果验证了该方法的可行性及准确性。
参考文献:
[1] Bartlett F D, Flannelly W G. Model verification of force determination for measuring vibration loads[J]. Journal of the American Helicopter Society, 1979, 24(2): 10-18.
[2] Hillary B,Ewins D J. The use of strain gauges in force determination and frequency response function measurements[C]. Proceedings of the 2nd International Modal Analysis Conference ( IMAC), Florida, USA, 1984: 627-634.
[3] Doyle J F. Force identification from dynamic responses of a biomaterial beam?[J]. Experimental Mechanics, 1993, 33(1): 64-69.
[4] Desanghere G, Snoeys R. Indirect identification of excitation forces by modal coordinate transformation?[C]. Proceedings of the International Modal Analysis Conference & Exhibit, 1985,1: 685-690.
[5] Jacquelin E, Bennani A, Hamelin P. Force reconstruction: Analysis and regularization of a deconvolution problem[J]. Journal of Sound and Vibration, 2003, 265(1): 81-107.
[6] 高伟, 于开平,盖晓男. 范数拟合正则化方法在飞行器动态载荷识别中的应用[J].振动与冲击,2017, 36(9): 101-107.
Gao Wei, Yu Kaiping, Gai Xiaonan. Application of norm fitting regularization method in dynamic load identification of spacecrafts?[J]. Journal of Vibration and Shock, 2017, 36(9): 101-107.
[7] 缪炳荣, 周凤,陈翔宇,等.利用核函数和不同正则化方法的结构载荷识别混合技术研究[J].振动工程学报,2018, 31(4): 553-560.
Miao Bingrong, Zhou Feng, Chen Xiangyu, et al. Research of the structure load identification hybrid technology using kernel function and different regularization method[J]. Journal of Vibration Engineering, 2018, 31(4):553-560.
[8] Gaul L, Hurlebaus S. Identification of the impact location on a plate using wavelets[J]. Mechanical Systems and Signal Processing, 1998, 12(6): 783-795.
[9] Alajlouni Sa'ed, Albakri Mohammad, Tarazaga Pablo. Impact localization in dispersive waveguides based on energy-attenuation of waves with the traveled distance[J]. Mechanical Systems and Signal Processing, 2018, 105(5): 361-376.
[10] 顾慧芝, 聂君剑, 丁锡洪. 载荷识别的等效点动标定法[J]. 振动工程学报, 1997, 10(3): 329-334.
Gu Huizhi, Nie Junjian, Ding Xihong. An equivalent-point calibration method for dynamic load identifications[J]. Journal of Vibration Engineering, 1997, 10(3):329-334.
[11] 周晚林, 王鑫伟, 胡自力.?压电智能结构载荷识别方法研究[J].力学学报,2004,36(4): 491-495.
Zhou Wanlin, Wang Xinwei, Hu Zili. On load identification for piezoelectric smart structures[J]. Acta Mechanica Sinica, 2004, 36(4): 491-495.
[12] 嚴刚, 周丽. 加筋复合材料结构的冲击载荷识别[J].航空学报,2008, 29(5): 1150-1156.
Yan Gang, Zhou Li. Impact load identification for stiffened composite structure[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1150-1156.
[13] 祝德春, 张方, 姜金辉. 动态载荷激励位置识别技术研究[J]. 振动与冲击, 2012,31(1): 20-23.
Zhu Dechun, Zhang Fang, Jiang Jinhui. Identification technology of dynamic load location[J]. Journal of Vibration and Shock, 2012, 31(1): 20-23.
[14] 祝德春, 张方, 姜金辉,等. 动态载荷激励位置时域识别技术研究[J]. 振动与冲击, 2013, 32(17): 74-78.
Zhu Dechun, Zhang Fang, Jiang Jinhui, et al. Time-domain identification technology for dynamic load locations[J]. Journal of Vibration and Shock, 2013, 32(17): 74-78.
[15] 赵银燕, 李懿, 徐斌.梁上多点动载荷位置和大小识别方法研究[J].机械科学与技术,2014, 33(11): 1672-1676.
Zhao Yinyan, Li Yi, Xu Bin. Identification of the locations and amplitudes of multiple dynamical loads on elastic beam?[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(11): 1672-1676.
[16] Li Qiaofeng, Lu Qiuhai. Impact localization and identification under a constrained optimization scheme[J]. Journal of Sound and Vibration, 2016, 366(12): 133-148.
[17] Li Qiaofeng, Lu Qiuhai. Force localization and reconstruction using a two-step iterative approach[J]. Journal of Vibration and Control, 2017, 7(5): 1-12.
作者简介: 张 景(1993-),男,博士研究生。电话:18014850293; E-mail: 609356721@qq.com
通讯作者: 张 方(1962-),男,教授,博士生导师。电话:(025)84892227; E-mail: zhangfangyy@163.com

