新型贴片式扭振压电作动器的设计与实验研究

王瑞锋 王亮 贾博韬 金家楣 张泉 吴大伟

摘要： 提出了一种新型贴片式扭振压电作动器，采用沿厚度方向极化的方形压电陶瓷片，通过特殊的布置方式来激发矩形梁结构的扭转振动。该压电作动器通过不同的激励方式，可以激发出奇数阶和偶数阶扭转振动，具有结构简单、紧凑、易于加工和安装等特点。为了验证所提出的扭振压电作动器设计方案和工作原理的正确性，建立了理论模型，并采用有限元方法对其进行了动力学特性仿真分析，通过实验对原理样机进行了振动特性测试和动力学行为研究。结果表明，理论模型计算结果、有限元仿真计算结果和实验测试结果基本一致，验证了所提出的压电作动器设计方案的可行性和工作原理的正确性。

关键词： 扭振压电作动器; 动力学特性; 扭转振动; 贴片式; 谐响应

中图分类号： TH113.1    文献标志码： A    文章编号： 1004-4523（2021）03-0481-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.005

引 言

作动功能的压电作动器是利用压电材料的逆压电效应实现电能转化为机械能的器件[1]。根据振动模式，压电作动器通常分为纵向振动（纵振）、弯曲振动（弯振）、扭转振动（扭振）以及复合振动压电作动器四类。其中，扭振压电作动器广泛应用于超声电机[2?4]、压电传感器[5]、超声钻孔[6]、超声拉丝[7]、超声焊接[8?10]、深滚压加工[11]、超声喷涂[12]和微滴生成[13?14]等领域。

扭振压电作动器根据压电陶瓷片的安装方式和激励模式，可以分为夹心式和贴片式两种类型。夹心式扭振压电作动器是利用螺栓在一定预紧力的作用下将d15或d33振动模式的压电陶瓷片固定安装在两块弹性体的中间构成“三明治”结构。贴片式压电作动器是利用环氧树脂胶将d31振动模式的压电陶瓷片粘贴在弹性体表面构成压电复合结构。其中，利用d15振动模式的压电陶瓷片（俗称“扭振压电陶瓷片”）作为扭振激励源是最常用的：Harada等[14]和Morita 等[15]设计了基于扭振压电陶瓷片的夹心式压电作动器;鹿存跃等[16]总结介绍了采用d15剪切模式激发扭转振动的压电陶瓷环、筒以及压电陶瓷盘。利用压电陶瓷片的d33振动模式构建扭振压电作动器主要是通过特殊的结构将纵向振动转化为扭转振动：Al?Budairi等[17]和袁松梅等[18]在兰杰文换能器前端设置了椎体质量块，并沿着椎体轴线切割了螺旋槽，从而实现兰杰文换能器的纵向振动转化为整个结构的纵扭复合振动;Bai等[19]基于d33振动模式的压电陶瓷片设计了夹心式压电作动器，通过前端设置的两个结构转化器，将纵向振动转化为扭转振动。采用d31振动模式的压电陶瓷片构建的扭振压电作动器分为纵振诱发扭振和通过分区极化的压电陶瓷片的布置直接激励扭振两种类型：Yang等[20]将6片矩形压电陶瓷片均匀粘贴在圆柱金属基体表面，并且相邻2片压电陶瓷片连接的电信号存在90°相位差，由于相邻2片压电陶瓷片的不同步伸缩运动，间接激发圆柱体产生弯曲振动，进而诱发整个压电作动器的扭转振动;Friend等[21]在矩形梁上、下表面分别粘贴了三分区的矩形压电陶瓷片，其中压电陶瓷片中间分区未极化，且不通电，其余两个分区均沿压电陶瓷片的厚度方向极化，且极化方向相反;此外，上、下两片压电陶瓷片的对应位置分区极化方向相反。因此，上、下2片压电陶瓷片均会激发矩形梁产生相反方向的弯曲振动，从而激发出矩形梁的扭转振动。

虽然上述研究中设计的压电作动器均可以激发出扭振，但也存在一些問题：1） 采用压电陶瓷片的d15振动模式激发扭振，要求压电陶瓷片沿着周向极化，因此对压电陶瓷片的制造工艺提出了高要求，导致其制造难度大、价格昂贵;2） 采用螺旋槽诱发扭振的方法存在定子基体设计与加工困难，以及不利于压电作动器的小型化等问题，并且能量转化效率低;3） 采用贴片式压电陶瓷片直接激发金属基体的扭振，需要对压电陶瓷进行分区极化，增加了制造的难度和加工成本;4） 其他纵振诱导扭振的激励形式，也存在能量转化效率低以及所激发出的扭振不纯等问题。

针对上述问题，本课题提出了一种激励压电作动器扭转振动的新方法。利用压电陶瓷的d31振动模式，采用特殊的布置方式，将沿厚度方向极化的压电陶瓷片粘贴在金属基体表面构成扭振压电作动器。相比上述文献所提到的几种激励方式，该激励方式对压电陶瓷片的制造和安装工艺没有特殊要求，可以很容易地激励出扭转振动，具有结构简单、紧凑、经济性强等特点。

1 结构与工作原理

1.1 结构设计

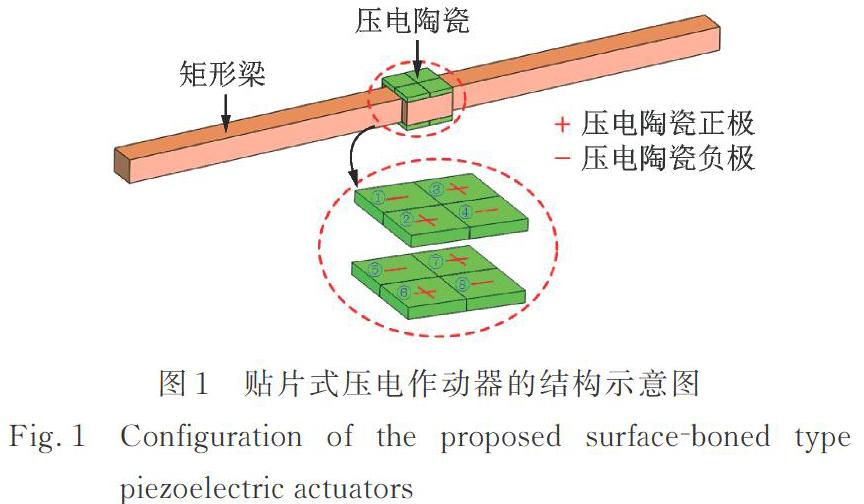
所提出的扭振压电作动器结构是由矩形梁和8片沿厚度方向极化的正方形压电陶瓷片组成，如图1所示。其中矩形梁由三段截面积不同的梁组成，包括两端截面积相同的弹性梁和横向尺寸略大的中间弹性梁。8片正方形陶瓷片均匀粘贴在中间弹性梁的上、下表面，同时相邻的2片压电陶瓷片的极化方向相反且上、下表面相对的2片压电陶瓷片极化方向相同。上述压电陶瓷的布置方式可以同时激发整个结构的奇数阶和偶数阶扭转振动。

1.2 激励方式

通过沿厚度方向极化的压电陶瓷片的特殊布置方式激发结构的扭转振动是本文所提出的压电作动器的一个显著特点。为了实现压电作动器的奇数阶和偶数阶扭转振动的激发，采用了两种不同的电信号施加方式，如图2所示。当压电作动器的所有压电陶瓷片连接相同的电压信号时，可以产生奇数阶扭转振动，如1阶和3阶扭振，如图2（a）所示。当压电陶瓷组左端上、下4片压电陶瓷（压电陶瓷片①，②，⑤和⑥）施加电信号A，压电陶瓷组右端上、下4片压电陶瓷（压电陶瓷片③，④，⑦和⑧）施加电信号B，并且两相电信号在时间上具有π的相位差，可以产生偶数阶扭转振动，如2阶和4阶扭振，如图2（b）所示。本文主要研究压电作动器的前4阶扭转振动。

2 理论建模

对提出的扭振压电作动器建立了理论模型，以揭示其动力学特性。

由高等材料力学可知，矩形梁的扭矩与扭转角关系为

式中 φ（x，t）为矩形梁沿轴向任意坐标x和任意时刻t的转角函数;β1为与b/a有关的系数;G为剪切模量;2a=h为矩形梁的高度，2b=W为矩形梁的宽度。

根据扭振偏微分方程，可以得出

利用莫尔圆原理可得梁的表面主应力方向（与x轴夹角）上的应变和扭转角应变之间的关系[22]。

式中 为梁的表面主应力方向上的应变，为沿轴向任意坐标x位置的扭转角应变函数。

矩形梁的扭转角应变与扭转角之间的关系为[23]

对于压电复合梁，存在压电本构方程：

式中 为短路柔度常数，为压电应变常数，为自由介电常数，和分别为沿纵向的应变和应力，和分别为极化方向的介电电位移和电场。

由于压电材料在1?2平面各向同性，所以主应面上的主应力Tp可以表示为

根据材料力学理论，在纯剪切状态下，压电体主应面上的正应力等于对应切平面的切应力

压电复合梁截面上的总扭矩为

压电复合梁的扭转角与扭矩分别为：

联立方程（4），（5），（13）和（14），根据连接界面处合力矩为零和扭转角相等的法则，结合电学边界条件和机械边界条件可以算出扭转角及扭矩的大小。

3 有限元仿真分析

3.1 有限元建模

为了验证所提出的扭振压电作动器工作原理的正确性，采用有限元仿真软件Ansys/Workbench对其进行仿真分析。首先确定扭振压电作动器的边界条件：机械边界条件和电学边界条件。由于所提出的压电作动器工作在自由?自由的边界条件下，因此机械边界条件是自由状态。电学边界条件是指施加在压电陶瓷片上的电信号，在此以100 V电压作为电学边界条件。压电作动器的弹性梁采用磷青铜材料，压电元件为PZT?8（无锡海鹰集团提供，机电耦合系数Kp=0.31，品质因数Qm=1500，尺寸为5 mm×5 mm×1 mm），具体材料的参数如表1所示。根据压电陶瓷片的尺寸以及布置方式，确定了压电作动器的尺寸，如图3所示，具体尺寸参数如表2所示。在有限元建模中，采用六面体单元划分网格，网格单元尺寸为0.8 mm，共有4884个网格单元，所提出的压电作动器的有限元模型如图4所示。

3.2 谐响应分析

对有限元模型进行了谐响应分析，得到了以压电作动器的扭转角作为参量的频率响应特性曲线，如图5所示，其中实线为压电作动器激发的奇数阶扭转振动频响曲线，虚线为换能器激发的偶数阶扭转振动频响曲线。计算得到的前4阶扭振的谐振频率分别为7.946，12.018，23.820和26.277 kHz，并且可以看出偶数阶扭振的幅值小于奇数阶扭振的幅值。

在计算得到的谐振频率的基础上，仿真计算了前4阶扭振的振型，如图6所示。可以看出，计算得到的前4阶扭振振型与设计的振型一致，说明压电作动器的工作原理是可行的。

为了验证理论模型的正确性，用MATLAB软件计算了该压电作动器理论模型的前4阶扭振振型，并与有限元仿真软件Ansys/Workbench提取出的前4阶扭振振型进行比较，如图7所示。图7（a）为压电作动器奇数阶扭振振型对比图，图7（b）为压电作动器偶数阶扭振振型对比图。从图中可以看出，理论模型和有限元软件的计算结果基本一致，从而验证了所建立的理论模型的正确性。

为了研究压电作动器的动力学特性，在有限元模型上选取了A点、B点和C点三个点作为研究对象，如图4中所示。计算得到了前4阶扭振模态下上述3个点的动力学特性，如图8所示。从图中可以看出，每阶扭振模态下A点与C点在y和z两个方向上均产生运动且耦合运动方向基本正交，B点位于扭转振动的中性面上，所以基本只在y方向运动，符合扭振模态的振动特性。由于弹性体在扭转振动的过程中，存在材料的泊松效应（回转效應），导致径向产生微幅的收缩运动，所以每阶扭振模态下3个目标点的运动轨迹均为椭圆。从图中可以看出1阶、2阶和4阶扭振模态下3个目标点的轨迹基本呈直线状（即椭圆的短轴非常短），而3阶扭振模态下3个目标点的椭圆轨迹较为明显，说明3阶扭振的径向收缩运动大于其他3阶扭振的径向收缩运动。

4 实验研究

为了进一步对所提出的扭振压电作动器的设计方案和工作原理以及有限元仿真结果进行验证，加工制造并安装了原理样机，如图9所示。为了测试原理样机的振动特性，搭建了基于多普勒三维激光测振仪（PSV 500， Ploytec Company， Germany）、两台功率放大器、一台示波器和气浮台的实验平台，如图10所示。在测试过程中，将扭振压电作动器原理样机的上表面作为测试面，用来接收和反射多普勒三维激光测振仪所发出的激光束。利用上述实验平台对扭振作动器进行扫频和定频实验。设置扫率范围5?35 kHz，采样频率为6400 Hz，对原理样机进行扫频试验，确定各阶振动模态的共振频率点。然后根据扫频测试得到的共振频率点，进行定频实验，测试原理样机在每一共振频率点处的振型。最后基于实验得到的原理样机的每一阶扭振模态的共振频率进行动力学特性测试，在激光投射面上划分所需网格并选取测试点，测试其振幅随电压的变化趋势。

4.1 频率响应特性

首先，利用实验平台对原理样机进行了频率响应特性测试。由于无法测试得到原理样机的扭转角，因此在测试过程中利用扭振压电作动器测试面的位移来表征频响特性。

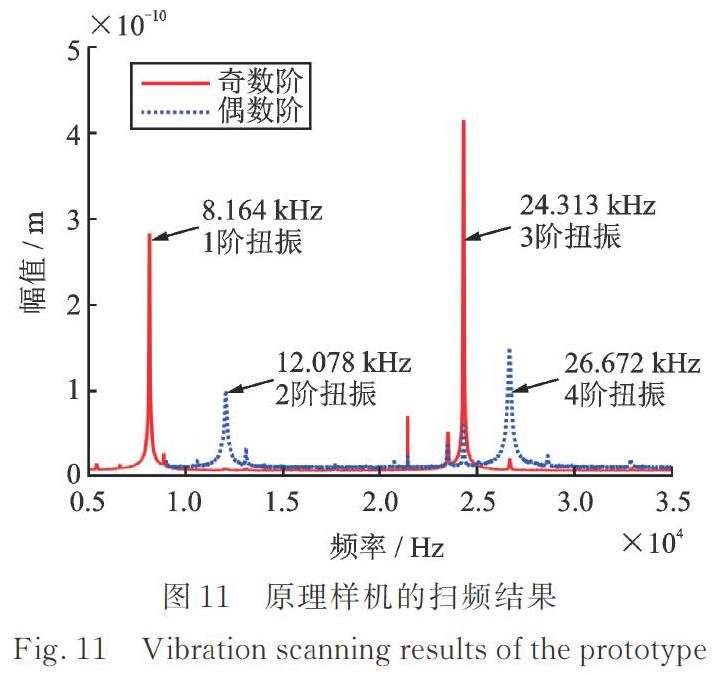
原理样机前4阶扭振模态的扫频实验结果如图11所示。可以看出，压电作动器的奇数阶扭振模态的幅值大于偶数阶的幅值，与有限元仿真分析结果基本一致。频率响应特性得到的原理样机前4阶谐振频率分别为8.164，12.078，24.313和26.672 kHz。与理论模型计算、有限元仿真计算和实验测试得到的压电作动器前4阶谐振频率进行了比较，如表3所示。其中，差值比1为理论模型计算结果与实验得到的谐振频率的差值比，差值比2为有限元计算结果与实验得到的谐振频率的差值比。从对比结果可以看出，差值比1最小为0.52%，最大为2.02%;差值比2最小为0.5%，最大为2.67%，说明所建立理论模型的正确性，以及有限元计算的准确性。理论模型计算结果、有限元计算结果与实验结果的差别主要来源于：（1）在理论模型与有限元模型中没有考虑胶层对压电作动器振动特性的影响;（2）压电作动器在加工制造、装配以及测试过程中所产生的误差;（3）选用的材料参数理论值与实际值有差别。

4.2 扭振振型

为了更详细地描述扭振压电作动器原理样机的振动特性，利用搭建的实验平台测试了前4阶扭振模态下的振型，如图12所示。测试过程中，机械边界条件为两端自由，电学边界条件为20 V的电压。从实验结果可以看出，原理样机前4阶的扭振振型与有限元仿真计算结果完全一致，从而进一步验证了所提出的扭振压电作动器方案和工作原理的正确性。

4.3 动力学特性

为了测试扭振压电作动器原理样机的动力学特性，以其端部的动态响应特性作为参考标准。由于扭转角难以直接测量，本文选择压电作动器端部的两个相邻面上的6个点作为测试目标点，如图13所示。其中B点、E点理论上位于上表面与侧表面的中性面上，A点、C点以B点为对称中心，位于上表面的边缘位置，D点、F点以E点为对称中心，位于侧表面的边缘位置。利用多普勒三维激光测振仪在前4阶扭振谐振频率下测试了上述6个点的位移幅值，从而间接地反映出压电作动器原理样机输出的扭转动力学特性。

压电作动器原理样机的前4阶扭振动力学特性测试结果如图14所示。可以看出，在同一电压下，B点与E点处的位移基本为0，说明这两点位于扭转振动的中性面上;A点与C点的振动位移关于B点基本对称;D点与F点的振动位移关于E点基本对称;A点与F点运动方向相反;C点与D点运动方向相反。此外，从图中的测试结果可以看出，压电作动器的奇数阶扭振的振幅大于偶数阶的振幅，同时每一阶扭振的振动幅值随着电压升高逐渐线性增加。上述6个点的动力学特性可以间接反映出压电作动器端部的扭转运动，并且验证了本文所提出的压电作动器方案设计和工作原理的正确性与有效性。

有限元仿真计算结果和实验结果均表明本文所提出的激励方式能够激发出扭振，从而验证了本文所提出的扭振压电作动器设计方案和工作原理的可行性。此外，理论分析和实验结果均表明扭振压电作动器偶数阶扭振的振幅明显小于奇数阶扭振的振幅，这是由于扭振模态下压电陶瓷片布置在奇数阶扭振的节点位置，而不处于偶数阶扭振的节点位置，导致偶数阶扭振的幅值相对较小[24]。但仅通过改变激励信号的相位，就可以在一个压电作动器上分别激发出奇数阶与偶数阶扭振模态，这本身就是本文所提出的扭振压电作动器激励方式的优势所在。

5 结 论

本文采用沿厚度极化的方形压电陶瓷通过特殊的布置方式构建了一种工作在扭转振动模式下的新型贴片式压电作动器。通过改变激励信号的相位，可以分别激发出压电作动器的奇数阶扭振和偶数阶扭振，降低了扭振压电作动器对压电陶瓷片制造工艺的特殊要求，并且简化了压电作动器的结构。通过理论模型、有限元分析方法和实验研究验证了所提出的新型压电作动器设计方案和工作原理的正确性。本文所提出的扭振压电作动器具有结构简单、紧凑，激励方式简便、有效，易于加工、安装的特點，并且有利于扭振压电作动器的微型化。

参考文献：

[1] Ru C， Liu X， Sun Y. Nanopositioning Technologies || Piezoelectric Motor Technology： A Review[M]. Switzerland： Springer International Publishing， 2016：33-59.

[2] 杨  淋， 赵淳生. 大力矩应力型纵扭复合超声电机[J]. 振动、测试与诊断， 2012，32（S1）：126-131.

Yang Lin， Zhao Chunsheng. Stress-type hybrid ultrasonic motors using longitudinal and torsionali vibration modes with large torque[J]. Journal of Vibration， Measurement & Diagnosis， 2012， 32（S1）：126-131.

[3] 易幼平， 钟  掘. 复合型超声马达纵-扭振动固有频率简并研究[J]. 振动工程学报， 2005， 18（2）：194-199.

Yi Youping， Zhong Jue. Study on eigenfrequency degeneration of longitudinal and torsional vibrations in a hybrid ultrasonic[J]. Journal of Vibration Engineering， 2005， 18（2）：194-199.

[4] 娄军强， 魏燕定， 杨依领，等. 空间柔性机械臂弯扭耦合振动的主动控制研究[J]. 振动工程学报， 2014， 27（3）：400-407.

Lou Junqiang， Wei Yanding， Yang Yiling， et al. Active control of bending-torsion-coupled vibration of a space flexible manipulator[J]. Journal of Vibration Engineering， 2014， 27（3）：400-407.

[5] Melchor J， Rus G. Torsional ultrasonic transducer computational design optimization[J]. Ultrasonics， 2014， 54（7）：1950-1962.

[6] Wang X， Jiao F， Wang D， et al. Development of a longitudinal-torsional ultrasonic vibration-aided drilling system for drilling carbon fiber-reinforced polymer materials[J]. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering， 2019， 233（12）：1-11.

[7] Yang C， Shan X， Xie T. A new piezoelectric ceramic longitudinal-torsional composite ultrasonic vibrator for wire drawing[J]. Ceramics International， 2015， 41：S625-S630.

[8] Kaneko S， Nomoto S， Yamamori H， et al. Load characteristics of a bolted Langevin torsional transducer[J]. Ultrasonics， 1996， 34（2-5）：239-241.

[9] Kaneko S， Takeda K， Yamamori H， et al. Load characteristics of bolted Langevin torsional transducer II[J]. Ultrasonics， 1998， 36（1-5）：111-113.

[10] Adachi K， Saito M. Construction of torsional-vibration systems with a hollow cylindrical bolt-clamped langevin-type transducer and their application to ultrasonic plastic welding[J]. International Journal on Software Tools for Technology Transfer， 1995， 34（Part 1， No. 5B）：2735-2739.

[11] 郑建新， 侯雅丽. 纵-扭复合振动超声深滚加工工艺试验[J]. 中国机械工程， 2016， 27（19）：2636-2640.

Zheng Jianxin， Hou Yali. Technological experiments of ultrasonic deep rolling with longitudinal torsional vibration[J]. China Mechanical Engineering， 2016， 27（19）：2636-2640.

[12] Tsuyuki S， Kanda T， Suzumori K， et al. Low flow rate spraying using a torsional ultrasonic transducer[C].2015 IEEE International Ultrasonics Symposium， Taipei， China，2015：1-4.

[13] Kishi T， Kiyama Y， Kanda T， et al. Microdroplet generation using an ultrasonic torsional transducer which has a micropore with a tapered nozzle[J]. Archive of Applied Mechanics， 2016， 86（10）：1751-1762.

[14] Harada T， Ishikawa N， Kanda T， et al. Droplet generation using a torsional Langevin-type transducer and a micropore plate[J]. Sensors and Actuators A：Physical， 2009， 155（1）：168-174.

[15] Morita T， Yoshida R， Okamoto Y， et al. A smooth impact rotation motor using a multi-layered torsional piezoelectric actuator[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control， 1999， 46（6）：1439-1445.

[16] 鹿存跃， 周铁英， 陈宇，等. 压电陶瓷剪切模式用于超声波电动机的研究[J]. 微特电机， 2007，（10）：14-17.

Lu Cunyue， Zhou Tieying， Chen Yu， et al. Application research of piezoelactric ceramic components with shear modes in ultrasonic motors[J]. Small & Special Electrical Machines， 2007，（10）：14-17.

[17] Al-Budairi H， Lucas M， Harkness P. A design approach for longitudinal-torsional ultrasonic transducers[J]. Sensors and Actuators A： Physical， 2013， 198：99-106.

[18] 袁松梅， 唐志祥， 吳奇， 等. 纵扭超声换能器设计及其性能测试研究[J]. 机械工程学报， 2019，55（1）：139-148.

Yuan Songmei， Tang Zhixiang， Wu Qi， et al. Design of longitudinal torsional ultrasonic transducer and its performance test[J]. Journal of Mechanical Engineering， 2019， 55（1）：139-148.

[19] Bai D， Quan Q， Tang D， et al. Design and experiments of a novel rotary piezoelectric actuator using longitudinal-torsional convertors[J]. IEEE Access， 2019， 7： 22186-22195.

[20] Yang L， Ren W， Ma C， et al. Mechanical simulation and contact analysis of the hybrid longitudinal-torsional ultrasonic motor[J]. Ultrasonics， 2020，100：105982.

[21] Friend J， Nakamura K， Ueha S. A torsional transducer through in-plane shearing of paired planar piezoelectric elements[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control， 2004， 51（7）：871-878.

[22] Qian F， Zhou W， Kaluvan S， et al. Theoretical modeling and experimental validation of a torsional piezoelectric vibration energy harvesting system[J]. Smart Materials and Structures， 2018， 27 （4）：1-13.

[23] Adnan Elshafei M， Farid A， Omer A A. Modeling of torsion actuation of beams using inclined piezoelectric actuators[J]. Archive of Applied Mechanics， 2015， 85 （2）：171-189.

[24] 趙淳生.超声电机技术与应用[M]. 北京：科学出版社， 2010：23-38.

Zhao Chunsheng. Ultrasonic Motors Technologies and Applications[M]. Beijing： Science Press， 2010： 23-38.

作者简介： 王瑞锋（1988-），男，博士研究生。电话：（025）84891812;E-mail：ruifengw@nuaa.edu.cn

通讯作者： 王  亮（1990-），男，博士，讲师。电话：（025）84896661;E-mail：lwang@nuaa.edu.cn