非线性三参数隔振器动力学特性研究

刘海平 申大山 赵鹏鹏

摘要： 在保持三參数隔振器高频段良好的隔振效果基础上，采用X形结构引入几何非线性可有效抑制其谐振频段的动态响应。建立含X形结构的非线性三参数隔振器的动力学模型;采用谐波平衡法推导出其动态响应的解析表达式;通过与时域数值解和实验数据对比，验证了非线性三参数隔振器模型解析解的正确性。与传统两参数隔振器和传统三参数隔振器的力传递率相比，非线性三参数隔振器可以显著降低其谐振频率幅值;而高频区域的减隔振性能影响较小。讨论设计参数，如刚度比γ1和γ2、阻尼系数Ca、初始夹角θi、激励力幅值F0对隔振系统传递特性的影响。研究表明，刚度比γ1和γ2，阻尼系数Ca和初始夹角θi可影响隔振器在谐振频率和高频区域的减隔振效果，激励力幅值F0则对系统减隔振性能无影响。通过合理的参数选择，可使非线性三参数隔振器在谐振频率衰减效果优于传统三参数隔振器，且保证在高频区域的隔振性能不变。

关键词： 非线性特征; 三参数隔振器; X形结构; Ruzicka模型; Zener模型

中图分类号： O328; TB535    文献标志码： A    文章编号： 1004-4523（2021）03-0490-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.006

1 概 述

在振动工程领域，两参数隔振器（通常采用Voigt模型表征）是一类通用隔振器，但是，为了有效抑制谐振频率的振幅导致该类隔振器在高频段隔振效果变差，对应传递率下降率约为-20 dB/dec。由此，三参数隔振器（常采用Ruzicka模型或者Zener模型表征）应运而生，不仅可以有效抑制谐振频率振幅，而且高频区域传递曲线的下降速率也显著减小为-40 dB/dec[1?2]。由于三参数隔振器具有良好的减隔振性能，因此得到了更为广泛的工程应用[3?7]。

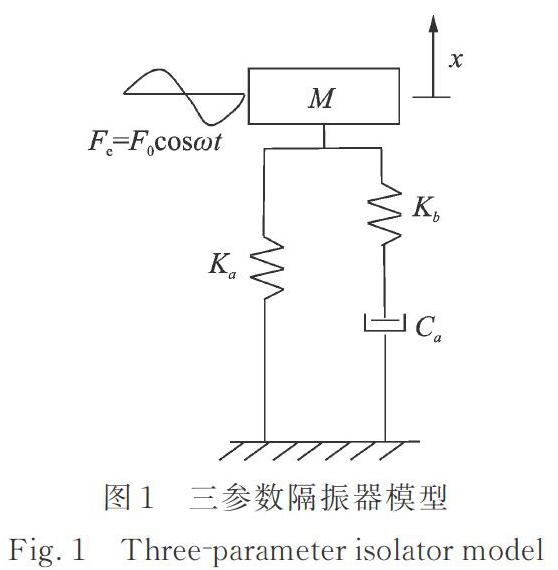
三参数隔振器模型，主要由主弹簧Ka、阻尼元件Ca和辅助弹簧Kb组成，如图1所示。主弹簧Ka与阻尼元件Ca并联安装共同支承系统质量M，阻尼元件Ca与辅助弹簧Kb串联并与基础连接。针对三参数隔振器的研究，Ruzicka[8]分别采用黏性阻尼元件和库伦摩擦阻尼元件构建三参数隔振器模型，并对其受迫振动响应进行了深入研究。Brennan等[9]重点针对三参数隔振器在自由振动和受迫振动（简谐激励和白噪声随机激励）条件下，从物理角度研究其特征方程不同特征根的物理含义，并给出相应的最优阻尼值。楼京俊等[10]研究发现在一定参数区域内三参数隔振器具有更优的抗冲击性能。

为了进一步改善三参数隔振器的减隔振性能，科研工作者开展了大量探索研究。考虑黏性流体阻尼器中流经阻尼孔黏性流体质量的影响，Shi等[11]建立隔振器的四参数Zener模型，研究发现该隔振器在高频段的减隔振性能得到了改善。为了改善三参数隔振器在谐振频率和高频区域的传递特征，Wang等[12]将与阻尼元件Ca串联的辅助弹簧Kb替换为立方刚度弹簧，Silva等[13]将主弹簧Ka替换为立方刚度弹簧。研究表明：不论将非线性立方刚度弹簧引入三参数隔振器的哪个位置均可在一定程度上改善其在高频段的减隔振性能，而对其他频段的传递率影响较小。因此，引入非线性元件将成为有效提升三参数隔振器减隔振性能的热点研究方向之一。

近年，内含几何非线性特征X形结构的高性能减隔振装置得到持续广泛的关注。Bian等[14?15]从仿生学角度提出采用X形结构引入非线性阻尼，研究发现谐振振幅极大衰减，而在其他频段由于阻尼增大并未使系统响应传递特性变差。Liu等[16]将多层X形结构与杠杆系统组合构成新型准零刚度隔振器，通过采用力控制可以有效调节系统反共振频率和低频范围的传递特性。Jing等[17]以建筑工程中普遍使用的冲击钻为研究对象，为了改善工人操作过程中所受恶劣力学环境的影响，创新性地提出采用多层X形结构构建反共振装置。仿真和试验均表明，在保证设备正常负载条件下，反共振装置可显著减小系统动态载荷的传递特性。Dai等[18]以航天器在轨非合作目标抓捕过程中周期或者冲击载荷作用下产生的微振动为控制目标，采用多层X形结构建立机械臂和末端执行机构之间的隔振装置。研究表明，多层X形结构组成的隔振装置可以有效控制自由悬浮状态卫星平台和被捕获目标之间的动态响应，且通过调整各设计参数可以灵活调整隔振装置的减隔振性能。Feng等[19]通过观察人体四肢运动过程中的力学关系，建立内含X形结构的反共振隔振器模型。研究表明，此类反共振隔振器具备优良的低频宽频减隔振性能。Cheng等[20]提出采用受拉伸载荷作用的X形结构建立准零刚度隔振装置。研究发现，通过引入几何非线性阻尼可有效控制谐振振幅，且在高频区域的减隔振性能未受其影响。综上，X形结构的几何非线性特征对隔振器的刚度和阻尼均具有放大功能，并且可以兼顾高/低频率区域不同的减隔振需求。

基于三参数隔振器和X形结构在减隔振方面的优良性能，本文在传统三参数隔振器中附加X形结构，提出一种含几何非线性三参数隔振器模型。利用谐波平衡法推导出该模型动态响应的解析表达式，并利用时域数值解对解析结果进行验证。通过与传统两参数隔振器和传统三参数隔振器对比，证明X形结构引入的几何非线性使非线性三参数隔振器在减隔振方面具有优势，能够显著降低谐振频率幅值，且对高频区域的传递特性未产生显著的负面影响。

2 非线性三参数隔振器建模

含几何非线性三参数隔振器模型如图2所示。与传统三参数隔振器Ruzicka模型或者Zener模型相比（参见图1），在阻尼元件Ca和辅助弹簧Kb之间安装X形结构，并将该结构一侧与辅助弹簧连接，另一侧接地;阻尼元件沿X形结构水平方向安装。从工程实际出发，阻尼元件（如：流体阻尼器）往往存在一定刚度，故在模型中引入与阻尼元件并联的辅助弹簧Kc。此处，为了保持与传统三参数隔振器模型一致，则考虑辅助弹簧Kc刚度为零。

模型中，实线为考虑负载时的静平衡状态，虚线为未考虑负载时的初始状态。X形结构由4根刚性铰接杆组成，单根刚性杆长度为l;与水平轴y的初始夹角为θi;受外部负载Fe作用，刚性铰接杆与水平轴夹角的变化量为φ;定义模型中坐标原点位于负载安装面中点，垂直向上为x轴正方向，水平向右为y轴正方向。

由图2所示力学模型，得到系统沿x轴方向的运动微分方程

其中，ωn为隔振器固有频率，τ为无量纲时间，γ1和γ2为隔振器刚度比，Ω为频率比，u1和u2为无量纲长度，ξ为阻尼比，f0为无量纲激励力。

进而化简得到

采用谐波平衡法对式（9）求解其稳态响应近似解，假设其稳态解为

式中 u10和u20为位移幅值。系统的稳态响应频率和激励频率相同。实际中，系统的响应也可能会引起其他频率的谐波。但是，受迫振动的响应中与激励频率相同的基础频率占主要部分，故式（10）并不影响对系统非线性特性的认识。

2.2 隔振性能

采用力传递率作为含几何非线性三参数隔振器隔振性能的评价指标。力传递率定义为传递到基础上的力幅值和激励力幅值之比，即

式中 T为非线性三参数隔振器的力传递率，ftr为通过隔振器传递到基础上的力。其中，通过非线性三参数隔振器传递到基础的力为

3 验证与对比分析

3.1 数值验证

为了验证几何非线性三参数隔振器动力学方程采用谐波平衡法求解的正确性，选取刚度比γ1=0.05，γ2=3，主弹簧刚度Ka=2000 N/m，刚性杆长度l=0.1 m，刚性杆与水平轴y的初始夹角为θi=60°，负载质量M=1 kg，阻尼系数Ca=1 N·s/m，激励力幅值F0=1 N。

选取计算时间为50 s，利用四阶龙格?库塔法得到隔振系统在定频激励下的数值解，选取稳态解的最大值为响应幅值并做归一化处理，由此得到位移响应的幅频曲线如图3所示。图中还给出系统的解析解。其中，“AS”表示解析解，“NS”表示数值解。可以看出，数值解与采用谐波平衡法求解方程（4）所得结果吻合良好，验证了本文求解过程的正确性。

3.2 实验验证

为了进一步验证所建模型及解析解的正確性，设计非线性三参数隔振器实验件并搭建实验装置如图4所示。

非线性三参数隔振器具体设计参数：M=2 kg，l=0.15 m，θi=65°，Ka=7500 N/m，Kb=26250 N/m，Kc=2250 N/m。另外，阻尼部分包括各部件之间相对运动产生的摩擦阻尼、结构材料阻尼和空气阻尼。

测试系统主要包括：电磁激振器、信号采集仪、信号发生器、功率放大器、计算机等。分别在惯性质量与电磁激振器连接位置和隔振器安装底板粘贴力传感器1#和2#。

图5分别给出实测和解析计算获得非线性三参数隔振器的力传递率曲线。可见，在50 Hz以下频段，解析结果和实测数据一致性较好;随着频率增加，实测力传递率曲线出现波动且与解析结果误差较大。该现象主要由隔振器高频局部模态所致，由于所建理论模型主要用于表征隔振系统在中低频段的减隔振效果，不包含高频模态的影响，说明理论模型和解析结果正确有效。

3.3 与其他隔振器模型对比

为了验证本文所提出的含几何非线性三参数隔振器模型的减振效果，将该模型与传统两参数隔振器模型（又称为Voigt模型）和三参数隔振器模型（又称为Ruzicka模型或者Zener模型参见图1）进行对比。此时不同类型隔振器的力传递率曲线如图6所示。其中，“V?M”表示Voigt模型，“R?M”表示Ruzicka模型和“M?R?M”表示非线性Ruzicka模型。

从图6中可以看出，在选用相同设计参数情况下，本文所提出的含几何非线性三参数隔振器模型和传统三参数隔振器模型在高频区域（即：频率比Ω>2）传递率曲线保持一致，且减隔振效果优于两参数隔振器。相比于传统三参数隔振器模型，通过X形结构引入几何非线性后非线性三参数隔振器模型的谐振振幅更小（由19.1减小为11.5），说明隔振系统在谐振频率的阻尼显著增大，有利于改善系统的减隔振性能。此外，受水平方向辅助弹簧Kc的影响，谐振频率比由1增大到1.07。在高频范围，传统三参数隔振系统和非线性三参数隔振系统的减隔振效果均优于两参数系统。

3.4 设计参数影响分析

相比传统三参数隔振器模型，含几何非线性三参数隔振器模型通过引入X形结构实现独特的力学特性。因此，本节重点针对非线性三参数隔振器的部分设计参数，即：刚度比γ1和γ2，阻尼系数Ca和刚性杆与水平轴y，初始夹角θi和激励力幅值F0对其减隔振效果的影响展开讨论。

3.4.1 γ1对系统传递率的影响

为方便对比，给出传统三参数隔振器模型的力传递率。保持其他设计参数不变，仅改变刚度比γ1分别取值-0.05，0，0.05和1.5。此时得到刚度比γ1对系统力传递率的影响如图7所示。可见：当系统振动频率较低时，系统力传递率等于0;当系统振动频率较高时，系统力传递率与传统三参数隔振器一致。在谐振频率附近，刚度比γ1增大，谐振振幅增大且谐振频率向高频移动。另外，隔振系统刚度比γ1<0时，系统频率向低频移动，有效隔振频带变宽;刚度比γ1=0时，X形结构引入的几何非线性系统参数与传统三参数隔振器完全相同，显见除谐振幅值大幅衰减之外，其他频点的响应特性均未发生变化;当刚度比0<γ1<1时，谐振频率及峰值略有增加但不明显;当γ1>1时，谐振频率向高频发生明显移动且峰值增加显著，由此导致系统中频段的减隔振效果变差。综上，合理选择刚度比γ1可分别实现“低刚度”或者“高阻尼”的振动控制效果。

3.4.2 γ2对系统传递率的影响

为了便于评价刚度比γ2对系统力传递率的影响，选择刚度比γ1=0，仅改变刚度比γ2分别取值-0.3，0.3，1和3。刚度比γ2对系统力传递率的影响如图8所示。可以看出：刚度比γ2<1时，随着刚度比增大系统谐振频率和峰值均增加，在高频范围隔振效果也随着刚度比增大而变差;刚度比γ2>1时，谐振频率对应峰值显著减小，高频范围减隔振效果进一步变差。综上，合理选择刚度比γ2可对系统谐振频率的峰值实现最优控制，但刚度比γ2增加使系统高频范围的隔振效果变差。

3.4.3 γ1和γ2组合参数对系统传递率的影响

为了进一步明确非线性三参数隔振器中不同刚度比γ1和γ2的组合特性对系统力传递率的影响。结合前述分析结果，当γ1≤0时更利于改善系统的减隔振性能且不影响其他频段的力传递特性。因此本部分重点讨论选择γ1≤0和不同γ2时，系统的力传递率曲线如图9所示。

首先，不考虑水平刚度的影响γ1=0，γ2的变化主要对系统高频段的减隔振效果产生影响，即：当γ2>1时高频段的减隔振效果由20 dB/dec提高为40 dB/dec;而在谐振频率附近的系统力传递特性不受γ2变化的影响。然后，分析水平刚度为γ1<0与γ2的组合刚度控制效果。可见，γ1<0和γ2>1时系统力传递特性得到显著改善，在谐振频率实现无谐振峰的控制效果，而在高频段的减隔振效果则与传统三参数隔振系统相同。但是，当γ1<0和0<γ2<1时系统在全频段的振动控制效果最差。

3.4.4 Ca对系统传递率的影响

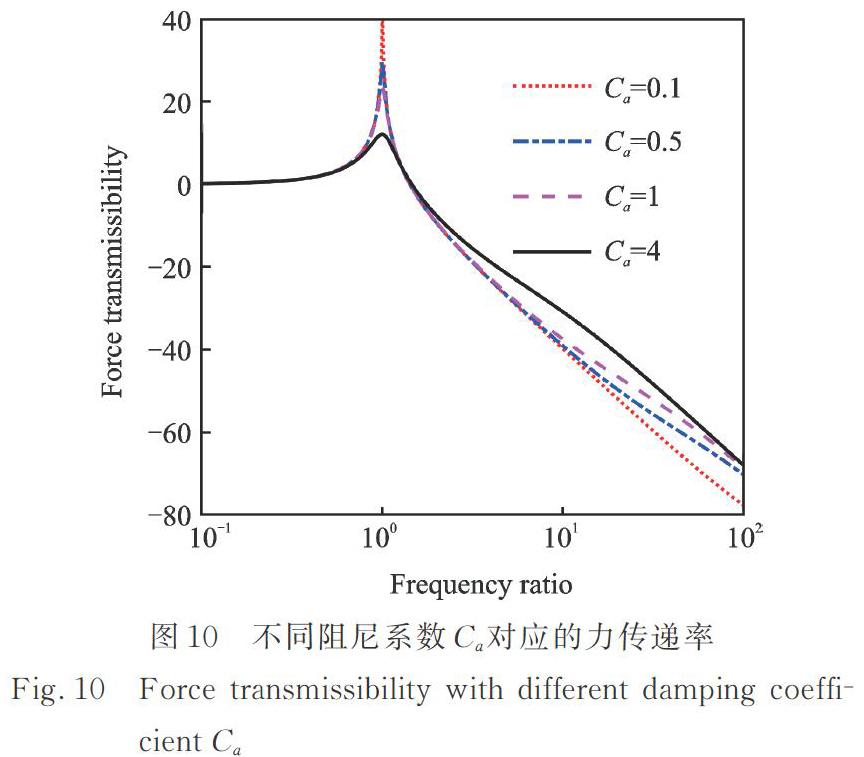
阻尼系数作为本文所讨论隔振器中唯一的耗能单元将显著影响隔振器在谐振频率和高频区域的振动控制效果。为了充分考虑阻尼系数的影响，选择刚度比γ1=0和γ2=3，保持其他參数不变，阻尼系数分别取值0.1，0.5，1和4 N·s/m。阻尼系数Ca对系统力传递率的影响如图10所示。可以看出，谐振频率处阻尼系数增大响应幅值减小;在高频区域，随着阻尼系数增大减隔振效果变差。此外，利用传统Zener模型的传递率可以给出最优阻尼比的解析表达式，但由于X形结构几何非线性特征的影响，非线性三参数隔振器无法直接给出阻尼系数Ca的最优值表达式。

3.4.5 θi对系统传递率的影响

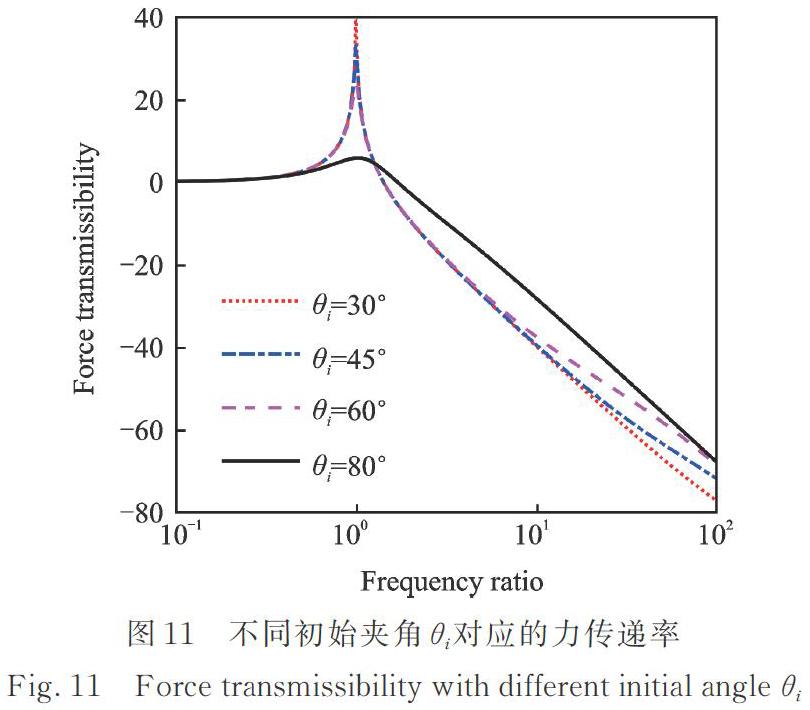
选择刚度比γ1=0和γ2=3，保持其他参数不变，仅改变刚性杆初始夹角θi分别取值30°，45°，60°和80°，对系统力传递率的影响如图11所示。由图可见，随着初始夹角增大系统输出阻尼增大，由此导致谐振幅值减小甚至达到无谐振峰的振动控制效果;在高频区域的隔振效果则受系统阻尼增大而变差。

3.4.6 F0对系统传递率的影响

选择力幅值F0=1 N和F0=10 N，保持其他参数不变，其对系统力传递率的影响如图12所示。由图12可见，在不同力激励幅值条件下，传递率曲线完全重合，由此可说明，激励力幅值的大小对该隔振系统的传递特性影响较小，基本可忽略。

另外，根据非线性三参数隔振器的力传递率公式（14）和（15），可见X形结构的杆长l和激励力幅值F0无关，也证明了上述关于力激励幅值F0影响的计算结果，故未考虑X形结构的杆长l对系统力传递特性的影响。而且，根据文献[21]，X形结构相比准零刚度和负刚度等非线性隔振系统不存在稳定性问题，故关于非线性三参数隔振器的稳定性问题也不在此讨论。

3.5 时域响应对比

通过分析几何非线性对三参数隔振器频域力传递率的影响，非线性三参数隔振器可以显著提高传统三参数隔振器在谐振频率的阻尼且谐振振幅被减小，如果参数选择合适可以保持系统高频区域的衰减效果不受影响。为了全面了解含几何非线性三参数隔振器的响应特性，以下分别在时间域和频率域讨论其受多频稳态激励的振动控制效果。

具体计算过程：针对不同隔振系统的运动微分方程，引入状态变量化简为一阶微分方程组;然后，采用四阶龙格?库塔法进行数值计算即可得到隔振器各部分的时域响应位移和速度;进而可以得到传递到基础的力的时域响应曲线;最后，采用快速傅里叶变换将时域结果转换到频率域，对比不同隔振系统对多频稳态激励的振动控制效果。

实际应用中，环境激励呈现宽频特性，假设隔振器所受外激励Fe=nωnt，n=0.1，0.5，1，5，10，20，30，40，50为多频激励，ωn为隔振系统固有频率。多频力激励下不同隔振器传递到基础的力在时间域和频率域的计算结果如图13和14所示。可以看出，非线性三参数隔振器对多频宽频激励的控制效果明显优于传统三参数隔振器，且系统谐振频率未发生变化。

4 结 论

利用X形结构引入几何非线性实现对三参数隔振器的改进，研究了此类隔振器的动力学特性。与传统三参数隔振器不同，通过对阻尼元件的几何非线性布置，系统的阻尼特性被放大，建立了非线性三参数隔振器的数学模型，采用谐波平衡法求解系统动力学方程，获得了隔振器的力传递率。通过与时域数值解对比，证明谐波平衡法求解结果的正确性。可以得到如下结论：

（1）设计参数中刚度比γ1和γ2，阻尼系数Ca和初始夹角θi可改善隔振系统在谐振频率和高频区域的减隔振效果，X形结构的杆长l和激励力幅值F0对减隔振效果没有影响;

（2）通过合理的参数选择，可使非线性三参数隔振器在谐振频率衰减效果优于传统三参数隔振器，且在高频区域的传递曲线衰减率与传统三参数隔振器保持一致;

（3）通过对时域响应和频域传递特性的对比，几何非线性使非线性三参数隔振器的振动控制性能明显优于传统三参数隔振器。

参考文献：

[1] Ruzicka J E， Derby T E. Influence of damping in vibration isolation[R]. Shock and Vibration Information Centre， US Department of Defense， 1972.

[2] 丁文镜. 减振理论[M]. 北京：清华大学出版社，1988.

Ding Wenjing. Theory of Vibration Isolation[M]. Beijing： Tsinghua University Press， 1988.

[3] Boyd J， Hyde T T， Osterberg D， et al. Performance of a launch and on-orbit isolator[C]. SPIEs 8th Annual International Symposium on Smart Structures and Materials， International Society for Optics and Photonics， 2001.

[4] Quenon D， Boyd J， Buchele P， et al. Miniature vibration isolation system for space applications[C]. SPIEs 8th Annual International Symposium on Smart Structures and Materials， International Society for Optics and Photonics， 2001.

[5] 刘兴天，钟  鸣，申军烽，等. 松弛型阻尼隔振模型的动刚度试验研究[J]. 噪声与振动控制，2016， 36（5）：180-182.

Liu Xingtian， Zhong Ming， Shen Junfeng， et al. Experimental analysis of the dynamic stiffness of a vibration isolation system with relaxation type damping[J]. Noise and Vibration Control， 2016， 36（5）：180-182.

[6] 谢溪凌，陈燕毫，刁建超， 等. 波纹管-黏滞流体隔振器特性与实验[J]. 噪声与振动控制，2017，37（4）：201-230.

Xie Xiling， Chen Yanhao， Diao Jianchao， et al. Experiment of an isolator fabricated with diaphragm bellows and viscous fluid[J]. Noise and Vibration Control， 2017， 37（4）：201-230.

[7] 孙靖雅. 三参数流体阻尼隔振器及并联隔振器的设计方法研究[D]. 上海：上海交通大学，2014.

Sun Jingya. Research on design method of three parameter isolator and parallel supported vibration isolation system[D]. Shanghai： Shanghai Jiao Tong University， 2014.

[8] Ruzicka J E. Forced vibration in systems with elastically supported dampers [D]. Cambridge： Massachusetts Institute of Technology， 1957.

[9] Brennan M J， Carrella A， Waters T P， et al. On the dynamic behavior of a mass supported by a parallel combination of a spring and an elastically connected damper[J]. Journal of Sound and Vibration， 2008， 309： 823-837.

[10] 楼京俊， 朱石坚， 唐斯密. Ruzicka隔振器在沖击隔离中的特性和作用[J]. 噪声与振动控制， 2011， 31（4）： 37-41.

Lou Jingjun， Zhu Shijian， Tang Simi. Study on effect of Ruzicka isolator on shock isolation[J]. Noise and Vibration Control， 2011， 31（4）： 37-41.

[11] Shi Wenku， Qian Chen， Chen Zhiyong， et al. Modeling and dynamic properties of a four-parameter Zener model vibration isolator[J]. Shock and Vibration， 2016， 6： 1-16.

[12] Wang Xing， Yao Hongxiang， Zheng Gangtie. Enhancing the isolation performance by a nonlinear secondary spring in the Zener model[J].Nonlinear Dynamics， 2017， 87（4）： 2483-2495.

[13] Silva Lucas de Haro， Goncalves Paulo J Paupitz， Wagg D. On the dynamic behavior of the Zener model with nonlinear stiffness for harmonic vibration isolation[J]. Mechanical Systems and Signal Processing， 2018， 112： 343-358.

[14] Bian Jing， Jing Xingjian. Nonlinear passive damping of the X-shaped structure[J]. Procedia Engineering，2017， 199： 1701-1706.

[15] Bian Jing， Jing Xingjian. Superior nonlinear passive damping characteristics of the bio-inspired limb-like or X-shaped structure[J]. Mechanical Systems and Signal Processing， 2019， 125： 21-51.

[16] Liu Chunchuan， Jing Xingjian， Li Fengming. Vibration isolation using a hybrid lever-type isolation system with an X-shape supporting structure[J]. International Journal of Mechanical Sciences， 2015， 98： 169-177.

[17] Jing Xingjian， Zhang Linli， Feng Xiao， et al. A novel bio-inspired anti-vibration structure for operating hand-held jackhammers[J]. Mechanical Systems and Signal Processing， 2019， 118： 317-339.

[18] Dai Honghua， Jing Xingjian， Wang Yu， et al. Post-capture vibration suppression of spacecraft via a bio-inspired isolation system[J]. Mechanical Systems and Signal Processing， 2018， 105： 214-240.

[19] Feng Xiao， Jing Xingjian. Human body inspired vibration isolation： Beneficial nonlinear stiffness， nonlinear damping & nonlinear inertia[J]. Mechanical Systems and Signal Processing， 2019， 117： 786-812.

[20] Cheng Chun， Li Shunming， Wang Yong， et al. Force and displacement transmissibility of a quasi-zero stiffness vibration isolator with geometric nonlinear damping[J]. Nonlinear Dynamics， 2017， 87（4）： 2267-2279.

[21] Wu Zhijing， Jing Xingjian， Bian Jing， et al. Vibration isolation by exploring bio-inspired structural nonlinearity[J]. Bioinspiration & Biomimetics， 2015， 10： 056015.

作者簡介： 刘海平（1982?），男，副教授。电话： （010）62334845;E-mail： liuhaiping@ustb.edu.cn