塔梁间设置BRB跨海斜拉桥减震约束体系及其地震反应

陈宝魁 王东升 李宏男 陈少林 李超

摘要： 提出在塔（墩）梁间设置防屈曲支撑（BRB）的斜拉桥耗能减震新型结构约束形式。以某跨海斜拉桥为工程背景，建立包括全漂浮体系、塔（墩）梁间设置黏滞阻尼器，以及塔梁间设置BRB的三类斜拉桥模型。通过比较不同约束方式斜拉桥结构在地震作用下桥塔的位移与弯矩反应，关键位置的相对位移与内力，以及耗能装置的滞回耗能响应等，确定设置BRB跨海斜拉桥新型减震约束体系的地震反应性态。研究发现斜拉桥结构设置黏滞阻尼器可以有效地减小支座以及塔（墩）梁间的相对位移，对塔顶相对于塔底的位移也有较好的控制，但明显增大了塔底及桥墩的弯矩。而设置BRB的斜拉桥结构可以大幅度降低塔（墩）底的弯矩，并且表现出了良好的耗能能力。

关键词： 斜拉桥; 防屈曲支撑; 减震耗能; 地震反应分析; 海底地震动

中图分类号： U448.27; U441+.3    文献标志码： A    文章编号： 1004-4523（2021）03-0452-10

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.002

引 言

中国拥有总长约为1.8万公里的海岸线，近年来建成包括港珠澳大桥在内的40余座跨海桥梁。考虑到东南沿海地区处于环太平洋地震带，且已发生的震害中，作为生命线工程的跨海桥梁的破坏将极大地阻碍震后救援与恢复工作。例如奥克兰海湾大桥（Oakland Bay Bridge）在1989年美国Loma Prieta地震中发生落梁，造成了极大的经济损失[1]。1995年日本Kobe地震中有几座跨海桥梁也发生了不同程度的破坏[2]。因此，本文尝试提出一种塔梁间设置防屈曲支撑（BRB）的大跨斜拉桥新型减震体系，即在桥塔（桥墩）与主梁间沿纵桥向安装BRB。

BRB属于金属耗能器范畴，其支撑内芯受外套筒约束，在拉压两个方向都具有稳定的滞回性能，自20世纪80年代中后期被文献[3]提出。在1994年美国Northridge地震和1995年日本Kobe地震后被美日逐步应用于建筑结构，1999年中国台湾集集地震后，更是在世界范围内得到重视。随着BRB产品屈服力与尺度的增长，已具备了在桥梁结构中应用的商业化产品支持。近年逐渐有学者进行了一些将BRB作为减震耗能构件在桥梁结构中应用的相关研究。Usami等[4]尝试将BRB用于钢桁架拱桥的减震加固中。Chen等[5]提出在钢桥排架桥墩间设置BRB的抗震设计方法。Celik等[6]尝试在钢桁架桥的两端横隔板位置布置BRB，讨论水平双向地震荷载作用下BRB对结构的抗震与耗能作用[7]。EI?Bahey等[8?10]发展了“保险丝””的设计理念，并将BRB应用于双柱墩分析其作为保险丝构件的耗能与滞回性能。其后，较多研究集中于BRB作为“保险丝”与减震构件在多柱排架墩间的应用与减震效果。谢文等[11?12]将BRB应用于大型斜拉桥的双柱式辅助墩，进行了相关试验与数值研究。孙治国等[13]基于“保险丝”的理念，利用BRB实现桥梁排架墩的抗震加固设计，验证了其对排架在地震中损伤的影响。石岩等[14]基于“保险丝”与损伤控制的抗震理念，发展了设置BRB桥梁排架墩基于位移抗震的设计方法。李晓莉等[15]以含高低墩的双柱式桥墩山区桥梁为例，研究了双柱式桥墩排架间设置BRB的耗能与减震效果。Dong等[16]开发出自复位防屈曲支撑（SC?BRB）并应用于双柱墩桥梁，通过试验与数值研究分析其对结构减震与限制残余位移的作用。Bazaez和Dusicka[17?18]利用大比例拟静力试验与数值分析，发现在钢筋混凝土桥梁排架墩间设置BRB可以有效地提高排架的横桥向抗震性能与位移延性，并起到“保险丝”构件的作用。Wang等[19]以某三跨钢筋混凝土梁桥为实例，通过在桥墩排架间设置BRB改善既有桥梁的抗震性能。Upadhyay等[20]比较了BRB与自复位耗能装置（SCED）对某既有桥梁排架墩加固后的残余位移及减震效果。

目前，BRB引入桥梁工程的研究主要集中于在排架墩间作为“保险丝”构件增强排架的延性与耗能能力，提高其横桥向的抗震性能。但以BRB作为大跨桥梁纵桥向的减震耗能构件及形成约束体系的研究十分有限。Lanning等[21]尝试以BRB替換黏滞阻尼器，安装于Vincent Thomas悬索大桥的纵桥向，发现在大跨桥梁的纵桥向布置BRB可以起到很好的减震耗能作用。本文针对大型跨海斜拉桥，尝试在塔（墩）梁间纵桥向设置BRB，替换既有跨海桥梁纵桥向设置的黏滞阻尼器。这种新型斜拉桥减震构造以BRB代替常用的黏滞阻尼器，将兼顾控制塔顶与主梁纵向位移，降低塔（墩）底内力，以及耗能减震的功能，并避免黏滞阻尼器可靠性弱、存在漏油及后期维护费用高的问题。设置BRB的斜拉桥结构在正常使用条件下，防屈曲支撑提供的刚度可使大跨度桥梁接近塔梁固结或弹性支承体系，也可以产生良好的抗风性能。

基于海底实测强震记录的分析，发现海底与陆地地震动的特性存在明显差异，海底水平向地震动反应谱具有更丰富的长周期成分，这可能对自振周期较高的跨海桥梁结构产生不利的影响[22?23]。因此，研究结合波动分析程序与有限元动力分析软件ADINA，实现了考虑桩?土?海水?跨海桥梁耦合的精细化地震反应分析模型，通过考虑海底地震动特性的非线性时程分析对BRB提高跨海桥梁纵桥向抗震性能的有效性进行分析。

1 桩-土-海水-跨海桥梁耦合地震反应分析模型

本文结合有限元动力分析软件ADINA与自编自由场地波动分析程序，建立包括海水层、海底覆盖层、跨海桥梁耦合的地震反应分析模型。

1.1 海底场地建模

首先，利用ADINA有限元软件模拟海底场地模型，其中海水层被视为势流体，并使用流固耦合边界（FSI）、流体无限边界（Infinite Element）和流体自由表面边界（Free Surface）等建立海底场地模型。在海底模型土体介质边界建立黏弹性人工边界，并利用自编地震波动程序对人工边界位置不同节点，输入考虑地震波动效应的等效应力，实现地震波在海底场地输入和传播过程的模拟。

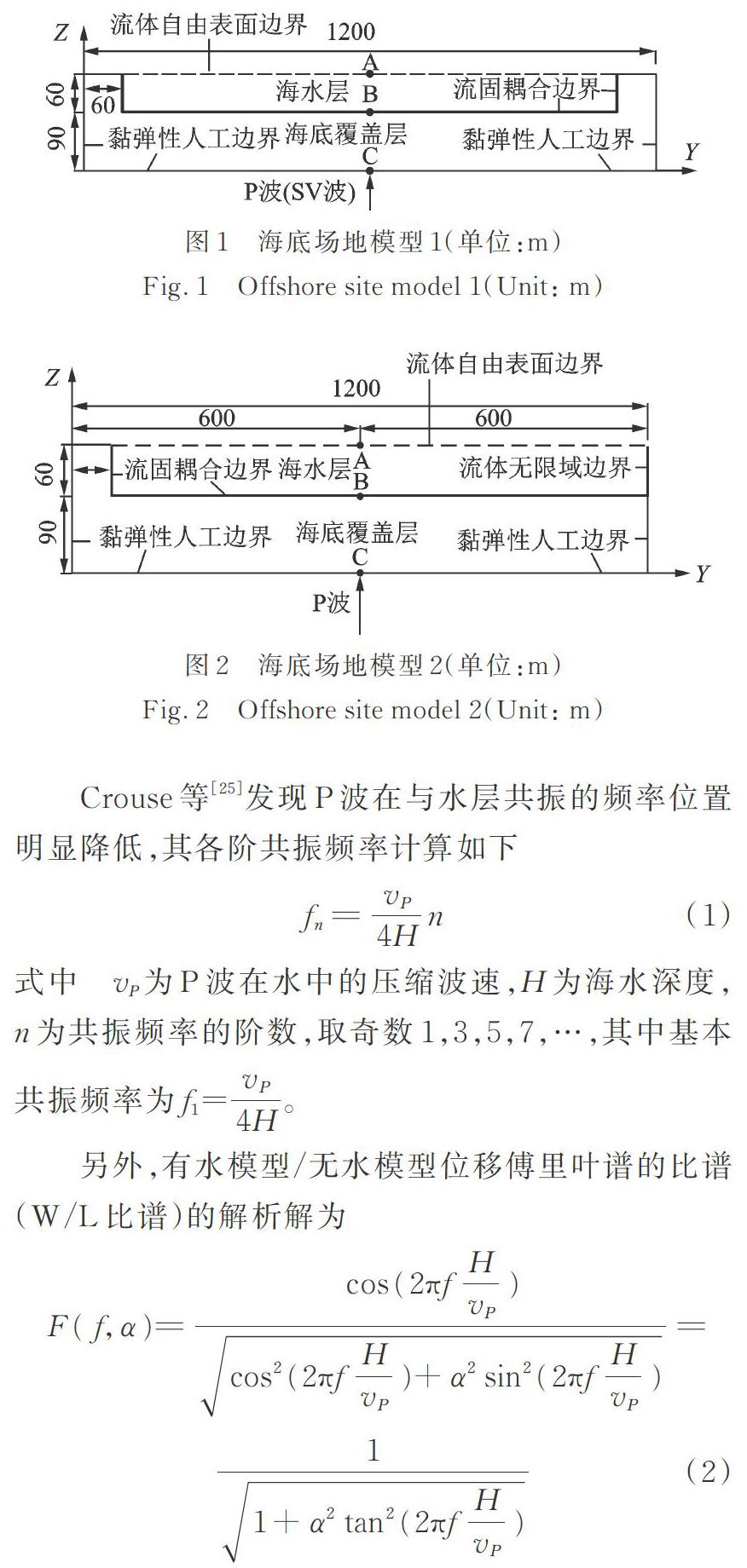
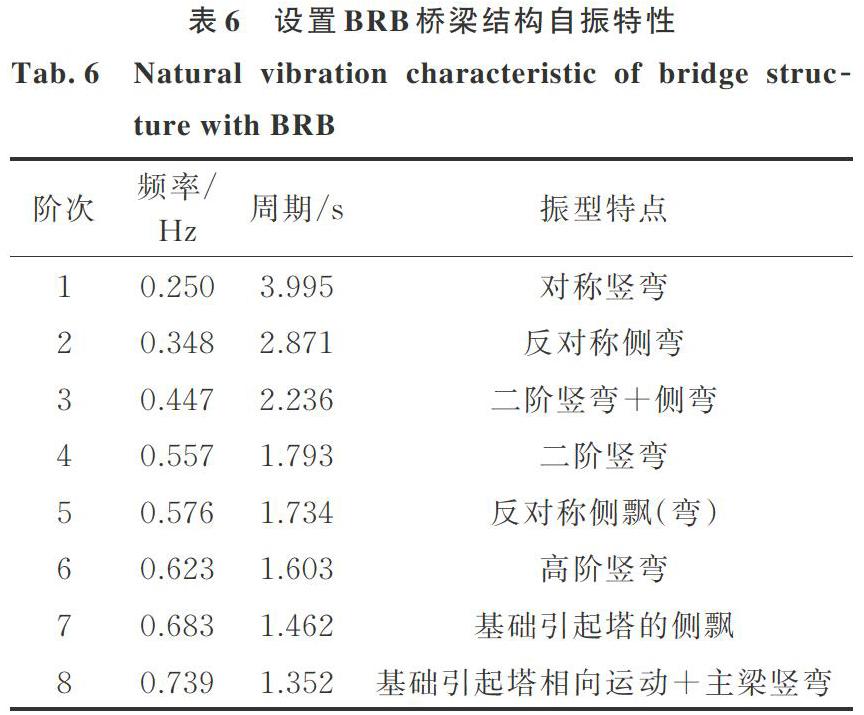
其次，为验证海底地震波动分析模型的准确性，以实际土层数据建立3类（无限半空间）单覆盖层海底场地模型，并以脉冲型P波作为输入荷载[24]。为了验证海水层势流体单元侧边界约束形式对分析结果的影响，分别建立如图1所示海水层双侧（岸）土层约束模型1，以及如图2所示左侧（岸）约束右侧应用流体无限域边界的模型2。另外，为了对比模型尺度对分析结果的影响，在模型2基础上，建立仅缩减模型宽度至600 m的模型3。

Crouse等[25]发现P波在与水层共振的频率位置明显降低，其各阶共振频率计算如下

另外，有水模型/无水模型位移傅里叶谱的比谱（W/L比谱）的解析解为

式中 H为水深;f为频率;α=ρ1vP/（ρ2v2）为海水与海床间的阻抗比;ρ1为水层的密度;ρ2为海底的密度;v2为海底覆盖层P波波速。

对比各海底场地模型海床（B点）W/L比谱的（平滑处理后）数值解与理论解如图3所示，发现3类模型的数值分析结果均与理论解十分接近。由此初步验证了本文提出的海底地震动波动分析方法的准确性，并确定了海水层侧边界约束形式与模型尺度对数值分析结果的影响。

1.2 桩-土-海水-跨海桥梁耦合地震反应建模

基于上述海底场地地震波动分析模型，输入基岩地震动可以得到海底场地中各节点地震响应。实际上，此时海床位置的地震反应已具备了海底地震动的特性，有利于更精确地分析跨海桥梁结构的地震反应。

在海底场地模型中加入桥梁结构，将桥梁的桩基础单元与海底覆盖层和海水层单元合理地连接，实现“桩?水”和“桩?土”间的耦合作用，将不同海底场地位置的等效地震应力作用于模型的黏弹性人工边界处，即实现考虑桩?土?海水?跨海桥梁耦合的地震反应分析。

2 设置BRB跨海斜拉桥新型减震结构建模

2.1 工程算例概述

以港珠澳跨海大桥青州航道桥作为工程案例，建立考虑桩?土?海水相互作用的跨海斜拉桥地震反应分析模型。该桥为双塔双索面钢箱梁航道桥，全桥长1150 m。斜拉桥通航孔主跨458 m，边跨236 m，边跨两侧连接110 m不设斜拉索的端跨。全桥主梁与桥塔间共布置56对扇形双索面斜拉索。桥塔位于主梁以上高117.822 m，主梁至承台高49.178 m。下部体系为现浇承台和钢管复合群桩基础[26]。

2.2 海底场地模型参数

本桥位于中国南海的伶仃洋，该海域的海底地形平坦地质条件简单，水深较浅，一般在5?15 m之间[27]。桥段水深10 m左右，覆盖层厚约为74.5?82.4 m[28]，通过工程海域的勘探作业，发现海底覆盖层主要分为四层，即厚度在20?30 m左右的淤泥软土层、黏土层、砂土层、以及分为上部强风化岩层与下部为弱风化岩层的基岩层。因此，研究建立130 m厚（包括海水层）海底场地模型，具体参数如表1所示。其中淤泥软土层参数通过考虑土体的孔隙率与孔隙水的饱和度，将含有水和土的双相介质转化为单相介质的参数进行计算[29]。

2.3 跨海桥梁结构计算模型

本文提出一种在塔（墩）梁间设置防屈曲支撑（BRB）的斜拉桥新型耗能减震结构。为了确定该结构的抗震与耗能能力，共建立包括全漂浮体系斜拉桥结构（模型I）、塔（墩）梁间设置黏滞阻尼器的斜拉桥结构（模型II）、以及塔（墩）梁间设置BRB的斜拉桥结构（模型III）的三类数值模型，比较各类（纵桥向）未约束和耗能减震约束体系跨海斜拉桥结构在地震作用下的响应。

模型Ⅰ：全漂浮体系（半漂浮体系）斜拉桥梁属于塔梁分离结构，在主梁与桥塔之间不设置水平向支承。

模型Ⅱ：塔（墩）梁间设置黏滞阻尼器的斜拉桥结构，塔梁分离，桥塔与主梁间除设置滑动铰支承外，还增加了纵桥向的耗能约束构件黏滞阻尼器。该数值模型中，以非线性阻尼的弹簧单元模拟黏滞阻尼装置。其中非线性阻尼力的输出方程为

式中 F为阻尼力;C为阻尼器阻尼系数;v为速度;α为速度指数（α的取值范围一般在0.1?2.0之间，抗震分析中常在0.3?1.0范围内取值）。从式（3）中不难发现，随阻尼系数C增大，黏滞阻尼器提供的阻尼力与耗能能力增加。速度指数α对阻尼器耗能的影响与速度v有關;当v<1时，阻尼力随α减小而增大;当v>1时，阻尼力随α增大而增大。本实例中桥塔（墩）设置黏滞阻尼器的相关设计参数如表2所示。

模型Ⅲ：塔（墩）梁间设置BRB的斜拉桥结构，是指在桥塔（墩）支座处布置连接主梁的沿纵桥向的BRB（如图4所示），数值模型中采用双线性理想弹塑性材料的桁架（truss）单元模拟。模型中BRB装置的设计参数参考实例桥黏滞阻尼器的设计屈服力、额定限位位移等参数设定，如表3所示，其中屈服位移取为黏滞阻尼器设计行程的1/10，使BRB尽早屈服耗能，但带来的问题是初始弹性刚度可能较大，对温度荷载不利。三个模型中，各模型的桥梁、海水、覆盖层场地的参数均相同。具体截面几何参数与材料参数不作赘述，可参见文献[30]。

2.4 地震输入时程的选择

对不同桥梁结构模型均输入3条选自日本KiK?net台网的基岩强震记录，其中2条选自临近海岸台站SZOH35在2006?04?21和2009?08?11地震中的强震记录，另1条强震记录选自日本3.11（2011?3?11）大地震福岛附近陆地台站FKSH20。3次地震的震级在Mw 5.8?Mw 9.0之间，所选地震波分别来自中震与大震的近海基岩台站。具体震源与强震台站信息参如表4所示。

该桥梁工程抗震设防标准以该桥结构完整性状态为2400年（基准期120年超越概率5%）为设计标准，基岩位置输入地震动峰值加速度（PGA）为190gal，地表处输入地震动的PGA为235gal。本文所选基岩强震记录按照设防标准进行调幅。利用自编波动分析程序将地震荷载采用外源波动输入法施加于模型的外人工边界节点。图5列出日本3.11地震的加速度时程曲线。限于篇幅，下文主要列出日本3.11地震的计算结果，并总结3次地震中对结构反应的主要共同认识。

3 设置BRB的跨海斜拉桥地震反应及比较

3.1 自振特性分析

自振特性分析使用ADINA软件的重启动功能，首先考虑桥梁结构在重力荷载作用下的受力平衡，然后以此为初始条件重启动进行自振特性分析，考虑了初始索力等几何非线性的影响。本文虽考虑了土层、海水等因素，但更关心的是桥梁结构的反应，因此在表5中仅列出了以桥梁结构振动为主的振型，以供参考。表5列出了全漂浮体系桥梁结构的前8阶的自振频率，因黏滞阻尼器不附加结构刚度，自身质量很小，因此表5中列出的自振特性同样适用于塔梁间设置黏滞阻尼器的斜拉桥结构。

表6列出了塔（墩）梁间设置BRB的桥梁结构的前8阶的自振频率，因BRB有初始弹性刚度，因此其自振频率明显高于漂浮体系斜拉桥。

3.2 桥塔的地震反应分析

以跨海斜拉桥在重力荷载作用下的受力平衡为初始条件，利用ADINA重启动进行地震反应时程分析。分析过程中阻尼模型采用Rayleigh阻尼，取计算模型的第1阶与第2階自振频率f1和f2控制α与β参数。因主梁为钢桥，阻尼比较小，取为3%。

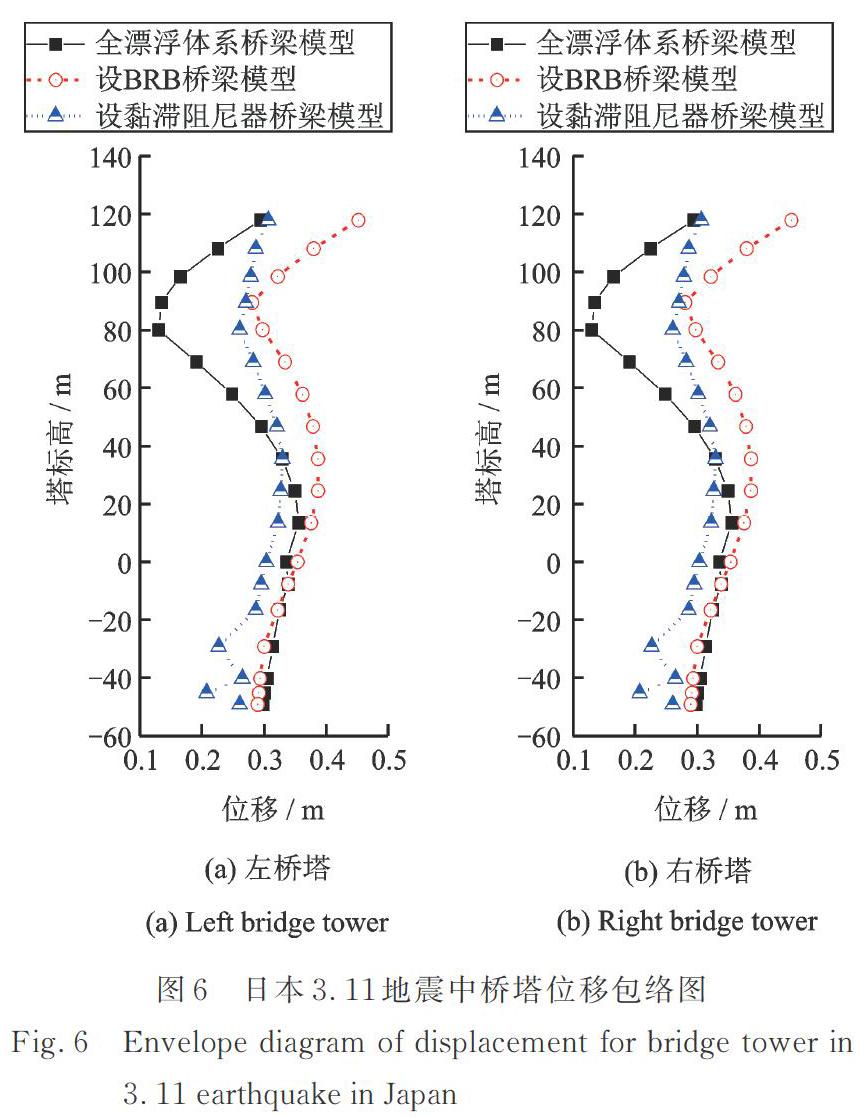
3.2.1 桥塔的位移反应

图6为桥塔在日本3.11地震中的位移包络图。图中左、右桥塔的位移包络图总体是一致的，但也有些许差异，可能原因是初始索力并非严格对称而地震波一般也非对称输入造成的。可以发现：在桥塔横梁以下（主梁支座处，标高0 m），漂浮体系结构桥塔的最大位移比另两个结构体系更大;在桥塔横梁以上，漂浮体系塔身位移相对于塔底的相对位移更大。由此可见，安置纵桥向约束耗能装置可以有效地控制桥塔绝对位移反应。

3.2.2 桥塔的弯矩反应

图7所示为桥塔在日本3.11地震中的弯矩包络图。图中各单元均为计算时间内最大反应的绝对值，因桥塔结构的内力反应主要由其各部分（截面）相对位移控制，相当于减去了地震动输入的绝对位移影响，因此作为桥塔反应分析的重点。在桥塔横梁以上，不同体系桥梁结构桥塔地震受力相近。在桥塔横梁以下至桥塔承台顶部，其受力几乎都表现为漂浮体系最小、设置BRB桥梁次之，设置黏滞阻尼器桥梁最大。其他两次地震中，桥塔位移及弯矩包络图的反应规律均与日本3.11地震一致。

3.3 关键节点位移与单元受力

为更全面了解水平地震输入下不同纵向约束体系斜拉桥的地震反应情况，表7和表8统计了在日本3.11地震水平地震波激励下，关键节点的位移与单元内力（弯矩与剪力）反应结果。从表中结果可见，设置黏滞阻尼器的桥梁结构可以有效地减小支座的相对位移（主梁与塔（墩），对塔顶相对于塔底位移也有较好的控制，但明显增大了塔底及辅助（过渡）桥墩的弯矩;设置BRB的桥梁结构对支座和塔顶的相对位移影响有限，但很大程度降低了塔底及辅助（过渡）桥墩的弯矩与剪力。其他两次地震中（2006?04?21与2009?08?11），跨海桥梁结构地震反应规律相同。

要说明的是，本文中BRB设计参数主要参考黏滞阻尼器的设计参数，以更好地与之对比，如果可以进一步地独立优化BRB设计参数，可能会发挥其更佳的减震效果。

3.4 黏滞阻尼器和BRB的反应比较

图8给出日本3.11地震激励下，在设置黏滞阻尼器桥梁结构中，左侧桥塔和过渡桥墩位置处黏滞阻尼器的反应骨架曲线和滞回曲线，前者为黏滞阻尼器的相对速度和黏滞阻尼力的关系，后者则是其相对位移和阻尼力的关系。

在日本3.11地震中桥塔与桥墩位置的黏滞阻尼器在地震荷载作用下均达到其设计阻尼力，其中桥塔位置黏滞阻尼器的阻尼力达到12000 kN，与设计阻尼力相近;桥墩位置黏滞阻尼器的阻尼力达到6000 kN，要大于设计阻尼力4500 kN，其最大相对速度达到0.8?1.2 m/s，要大于设计预估的0.5 m/s，这对抗震设计而言可能是危险的信号。因为无法准确预估黏滞阻尼器在未来地震中的最大受力，导致节点的设计面临困难。1995年Kobe地震中东神户大桥的黏滞阻尼器的锚栓就发生脱落破坏。在2006?04?21地震和2009?08?11地震中桥塔位置的黏滞阻尼器的阻尼力基本为6000 kN，桥墩位置黏滞阻尼器的阻尼力在3000 kN左右，由此可见，在2006?04?21地震和2009?08?11地震作用下，桥塔（墩）位置的黏滞阻尼器并未发挥其全部作用，它们的地震反应相对速度也小于预估值0.5 m/s。

图9给出了在日本3.11地震激励下设置BRB桥梁结构中，左侧桥塔（过渡墩）位置BRB的滞回曲线，即BRB的相对位移和其轴向力之间的关系曲线。从分析结果中发现，在3次地震中桥塔（墩）位置BRB的轴向力基本达到设计屈服轴力（桥塔位置BRB的设计屈服轴力为12000 kN，桥墩位置BRB的设计屈服轴力4500 kN）。同样，在日本3.11地震中BRB的地震反应较强烈，其滞回耗能反应也较大。

作为比较，表9量化了日本3.11地震中桥梁不同位置黏滞阻尼器与BRB的滞回耗能值，发现桥塔处设置BRB的滞回耗能明显高于桥塔处设置黏滞阻尼器的耗能。这点可以用来解释设置BRB桥梁模型中桥塔底部的内力小于设置黏滞阻尼器桥梁模型的现象。

4 结 论

本文提出了在塔（墩）梁间纵桥向设置防屈曲支撑（BRB）的跨海斜拉桥结构新的耗能减震方式，并与全漂浮斜拉桥结构和在塔（墩）梁间设置黏滞阻尼器的斜拉桥结构的地震反应进行了比较。数值计算中开发了考虑桩?土?海水?跨海桥梁结构耦合的精细化地震波动反应分析模型，并输入包含东日本3.11大地震在内的基岩地震波作为激励。就本文实例桥梁分析发现：

（1）设置黏滞阻尼器的斜拉桥结构可以有效地减小支座（或主梁与桥塔（墩）间）的相对位移反应，对塔顶相对于塔底（承台顶）的位移也有较好的控制，但明显增大了塔底及辅助（过渡）桥墩的弯矩。

（2）设置BRB的斜拉桥结构对支座和塔顶的相对位移控制较为有限，但相对于设置黏滞阻尼器的桥梁结构，很大程度降低了塔底及辅助（过渡）桥墩的弯矩。

（3）对东日本3.11大地震跨海斜拉桥地震反应进行比较，设置的BRB与黏滞阻尼器均达到设计轴力和设计阻尼力，并表现出了较好的耗能能力。但桥墩位置黏滞阻尼器的阻尼力与相对速度均超过设计值，存在损坏风险。

参考文献：

[1] Chou C C， Uang C M， Seible F. Experimental evaluation of compressive behavior of orthotropic steel plates for the New San Francisco-Oakland bay bridge[J]. Journal of Bridge Engineering， 2006， 11（11）： 140-150.

[2] Todor G， Fumio Y， Hiroshi I， et al. Response analysis of the Higashi-Kobe Bridge and surrounding soil in the 1995 Hyogoken-Nanbu Earthquake[J]. Earthquake Engineering and Structural Dynamics， 1998， 27（6）： 557-576.

[3] 杨昌民， 牧野俊雄， 李宏男. 防屈曲支撑的研究进展及其工程应用[J]. 建筑科学与工程学报， 2011， 28（4）： 75-85.

Yang Changmin， Makino Toshio， Li Hongnan. Research progress and its engineering application of buckling-restrained brace[J]. Journal of Architecture and Civil Engineering， 2011， 28（4）： 75-85.

[4] Usami T， Lu Z， Ge H. A seismic upgrading method for steel arch bridges using buckling-restrained braces[J]. Earthquake Engineering and Structural Dynamics， 2005， 34（4-5）： 471-496.

[5] Chen Z， Ge H， Kasai A， et al. Simplified seismic design approach for steel portal frame piers with hysteretic dampers[J]. Earthquake Engineering and Structural Dynamics， 2007， 36（4）： 541-562.

[6] Celik O C， Bruneau M. Seismic behavior of bidirectional-resistant ductile end diaphragms with buckling restrained braces in straight steel bridges[J]. Engineering Structures， 2009， 31（2）： 380-393.

[7] Wei X， Bruneau M. Analytical investigation of buckling restrained braces applications in bidirectional ductile end diaphragms for seismic performance of slab-on-girder bridge[J]. Engineering Structures， 2017， 141： 634-650.

[8] El-Bahey S， Bruneau M. Bridge piers with structural fuses and bi-steel columns. I： Experimental testing[J]. Journal of  Bridge Engineering， ASCE， 2012， 17（1）： 25-35.

[9] El-Bahey S， Bruneau M. Bridge piers with structural fuses and bi-steel columns. II： Analytical investigation[J]. Journal of Bridge Engineering， ASCE， 2012，17（1）：36-46.

[10] El-Bahey S， Bruneau M. Buckling restrained braces as structural fuses for the seismic retrofit of reinforced concrete bridge bents[J]. Engineering Structures， 2011， 33（3）： 1052-1061.

[11] 謝  文， 孙利民. 采用新型辅助墩的超大跨斜拉桥顺桥向损伤控制新体系研究[J]. 土木工程学报， 2014， 47（S2）： 28-34.

Xie Wen， Sun Limin. Studies on controlling structural systems of super long-span cable-stayed bridge by novel supporting pier in longitudinal direction [J]. China Civil Engineering Journal， 2014， 47（S2）： 28-34.

[12] 謝  文， 孙利民， 魏  俊. 附有结构 “保险丝” 构件的桥墩抗震性能试验研究及其应用[J]. 中国公路学报， 2014， 27（3）： 59-70.

Xie Wen， Sun Limin， Wei Jun. Experimental study on seismic performance of bridge piers with structural fuses and its application [J]. China Journal of Highway and Transport， 2014， 27（3）： 59-70.

[13] 孙治国， 华承俊， 石  岩， 等. 利用 BRB 实现桥梁排架基于保险丝理念的抗震设计[J]. 振动与冲击， 2015， 34（22）： 199-205.

Sun Zhiguo， Hua Chengjun， Shi Yan， et al. Seismic design of bridge bents with BRB as a structural fuse[J]. Journal of Vibration and Shock，2015，34（22）： 199-205.

[14] 石  岩， 王东升， 韩建平. 设置 BRB 桥梁排架墩基于位移抗震设计方法[J]. 土木工程学报， 2017， 50（7）： 62-68.

Shi Yan， Wang Dongsheng， Han Jianping. Displacement-based design method for bridge bents with buckling-restrained braces （BRBs） [J]. China Civil Engineering Journal， 2017， 50（7）： 62-68.

[15] 李晓莉，孙治国，刘  昕，等. 山区桥梁双柱式桥墩设置BRB的减震效果研究[J]. 振动与冲击， 2018， 37（22）： 173-180.

Li Xiaoli， Sun Zhiguo， Liu Xin， et al. Seismic responses of double column bridge bents with buckling-restrained braces in mountain areas[J]. Journal of Vibration and Shock， 2018， 37（22）： 173-180.

[16] Dong H， Du X， Han Q， et al. Performance of an innovative self-centering buckling restrained brace for mitigating seismic responses of bridge structures with double-column piers[J]. Engineering Structures， 2017， 148： 47-62.

[17] Bazaez R， Dusicka P. Cyclic behavior of reinforced concrete bridge bent retrofitted with buckling restrained braces[J]. Engineering Structures， 2016， 119： 34-48.

[18] Bazaez R， Dusicka P. Performance assessment of multi-column RC bridge bents seismically retrofitted with buckling-restrained braces[J]. Bulletin of Earthquake Engineering， 2018， 16（5）： 2135-2160.

[19] Wang Y， Ibarra L， Pantelides C. Seismic retrofit of a three-span RC bridge with buckling-restrained braces[J]. Journal of Bridge Engineering， 2016， 21（11）： 04016073.

[20] Upadhyay A， Pantelides C P， Ibarra L. Residual drift mitigation for bridges retrofitted with buckling restrained braces or self centering energy dissipation devices[J]. Engineering Structures， 2019， 199： 109663.

[21] Lanning J， Benzoni G， Uang C M. Using buckling-restrained braces on long-span bridges. I： Full-scale testing and design implications[J]. Journal of Bridge Engineering， 2016， 21（5）： 04016001.

[22] Chen B， Wang D， Li H， et al. Characteristics of earthquake ground motion on the seafloor[J]. Journal of Earthquake Engineering， 2015， 19（6）： 874-904.

[23] Chen B， Wang D， Li H， et al. Vertical-to-horizontal response spectral ratio for offshore ground motions： Analysis and simplified design equation[J]. Journal of Central South University， 2017， 24（1）： 203-216.

[24] 陳少林， 张莉莉， 李山有. 半圆柱型沉积盆地对SH波散射的数值分析[J]. 工程力学， 2014， 31（4）： 218-224.

Chen Shaolin， Zhang Lili， Li Shanyou. Numerical analysis of the plane SH waves scattering by semi-cylindrical alluvial valley[J]. Engineering  Mechanics， 2014， 31（4）： 218-224.

[25] Crouse C B， Quilter A. Seismic hazard analysis and development of design spectra for Maul A platform [C]. Proceedings of Pacific Conference on Earthquake Engineering， New Zealand， 1991： 137-148.

[26] 刘明虎， 孟凡超， 李国亮. 港珠澳大桥青州航道桥工程特点及关键技术[J]. 桥梁建设， 2013， 43（4）： 87-93.

Liu Minghu， Meng Fanchao， Li Guoliang. Engineering characteristics and key techniques of Qingzhou ship channel bridge of Hong Kong-Zhuhai-Macao bridge[J]. Bridge Construction， 2013， 43（4）： 87-93.

[27] 刘明虎， 孟凡超. 港珠澳大桥青州航道桥结构设计方案研究[J]. 中外公路， 2014， 34（1）： 148-153.

Liu Minghu， Meng Fanchao. Study on structural design program for Qingzhou ship channel bridge of Hong Kong-Zhuhai-Macao bridge[J]. Journal of China and Foreign Highway， 2014， 34（1）： 148-153.

[28] 廖建航. 港珠澳大桥岛隧工程精细化地质勘察管理[J].水运工程， 2013， （7）： 15-18.

Liao Jianhang. Management of fine soil investigation for Hong Kong-Zhuhai-Macao bridge island-tunnel project[J]. Port & Waterway Engineering， 2013， （7）： 15-18.

[29] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range[J]. The Journal of the Acoustical Society of America， 1956， 28（2）： 168-178.

[30] 陈宝魁. 海底地震动特性及跨海桥梁地震反应分析[D].大连： 大连理工大学，  2016.

Chen Baokui. Characteristics of offshore ground motions and seismic response analysis of sea-crossing bridges[D]. Dalian： Dalian University of Technology， 2016.

作者简介： 陈宝魁（1982?），男，博士，讲师，硕士研究生导师。电话：15180166744;E-mail： baokui_2000@163.com