摇摆-自复位双层桥梁排架墩抗震体系研究
孙治国 赵泰儀 韩强 王东升 亓兴军
摘要: 为实现摇摆?自复位(Rocking Self?Centering, RSC)双层桥梁排架墩的地震损伤控制设计和震后功能快速恢复,结合外置角钢、耗能钢筋、无黏结预应力筋设计了仅上层摇摆(模型1)、仅下层摇摆(模型2)以及双层均摇摆(模型3)的3种RSC双层排架墩。同时设计了一个普通钢筋混凝土(Reinforced Concrete, RC)双层排架墩(模型4)作为参考。建立了不同排架墩的抗震数值分析模型,并结合1个RSC单层排架墩的拟静力试验结果验证了建模方法的准确性。定义了RSC双层排架墩在强震下的失效准则,分析了近断层地震动下各双层排架墩的地震反应。结果表明:与普通RC双层排架墩相比,各RSC双层排架墩基本自振周期显著增大。PGA为0.1g时,RSC双层排架墩的角钢屈服并耗能。PGA为0.4g时,普通RC双层排架墩的层间残余位移角为0.82%,RSC双层排架墩的层间残余位移角接近0,且各RSC双层排架墩中预应力筋均未屈服;除模型1中的外置角钢未被拉断破坏外,其余模型中的角钢均被拉断。模型4下层桥墩截面的曲率延性系数远大于模型1下层(非摇摆层)桥墩以及模型2上层(非摇摆层)桥墩截面的曲率延性系数值。
关键词: 桥梁; 抗震结构; 摇摆?自复位; 双层排架墩; 失效准则
中图分类号: U441+.3;TU352.11 文献标志码: A 文章编号: 1004-4523(2021)03-0472-09
DOI:10.16385/j.cnki.issn.1004-4523.2021.03.004
引 言
为解决城市交通拥堵问题或受山区地形的限制,中国若干重点桥梁工程中采用了双层高架桥梁,并以双层排架墩为主要承重构件。代表性的工程有上海共和新路高架桥[1]、甘肃省武罐高速洛塘河特大桥[2]、以及跨越江河的公铁两用双层桥梁等[3]。由于横桥向地震动下,桥墩易形成矮墩且承受显著的变轴力影响,双层排架墩在震害中破坏严重,其抗震设计问题值得关注[4?6]。同时,随着地震损伤控制设计理论的发展,重大桥梁工程对桥墩(排架墩)的地震损伤破坏提出了更为严格的限制。如桥墩纵筋的屈服、混凝土的开裂或压碎破坏等都将严重影响桥梁的震后使用功能,传统的桥梁延性抗震设计理论已难以保证此类重大桥梁工程的地震安全。
在此背景下,摇摆?自复位(Rocking Self?Centering, RSC)桥墩受到了广泛重视[7?9]。该类结构的主要优点在于:其一,RSC桥墩基于预制拼装结构,可加快施工进度,减轻施工过程对现场交通和环境的影响;其二,强震下桥墩的摇摆反应将显著降低上部结构的地震力,通过合理的构造措施可有效抑制桥墩的损伤破坏;其三,RSC结构中广泛采用的无黏结预应力筋,可有效减少结构震后残余变形,有利于震后修复,快速恢复结构震后使用功能。目前,通过在RSC桥墩的接缝部位设置内置或外置耗能装置以增加结构耗能能力并减小结构的变形,成为新一代RSC墩柱的重要特点[10]。Cheng[11]完成了一个单层RSC排架墩模型的振动台试验,发现最大层间位移角超过5%时,结构仍无明显破坏和残余变形。ElGawady等[12]等则结合RSC单层排架墩模型的拟静力试验,讨论了基于外置角钢实现排架墩地震耗能和震后功能恢复的可行性。孙治国等[13]提出了外置角钢和内置耗能钢筋的RSC单层排架墩并建立了其抗震数值分析模型,讨论了近断层地震动下结构的地震反应。随着研究工作的不断深入和工程需求的增加,Thonstad等[14]完成了一座2跨桥梁模型振动台试验,使用的RSC单层排架墩采用承插式连接;Han等[15]则以北京市的一座RSC桥梁为背景,完成了3个含外置可替换耗能装置的RSC单层排架墩抗震拟静力试验。上述试验进一步证实了利用RSC体系实现桥梁地震损伤控制和震后功能恢复的有效性。
受上述研究背景的启发,结合双层桥梁排架墩的工程背景和地震损伤控制设计要求,本文设计了3种不同形式的RSC双层排架墩以及1个各层均不摇摆的普通钢筋混凝土(Reinforced Concrete, RC)双层排架墩。基于OpenSees平台建立了各双层排架墩的数值分析模型,在验证建模方法准确性的基础上,揭示了RSC双层排架墩在近断层地震动下的地震反应规律,以期为双层桥梁的抗震分析和设计提供参考。
1 RSC双层排架墩
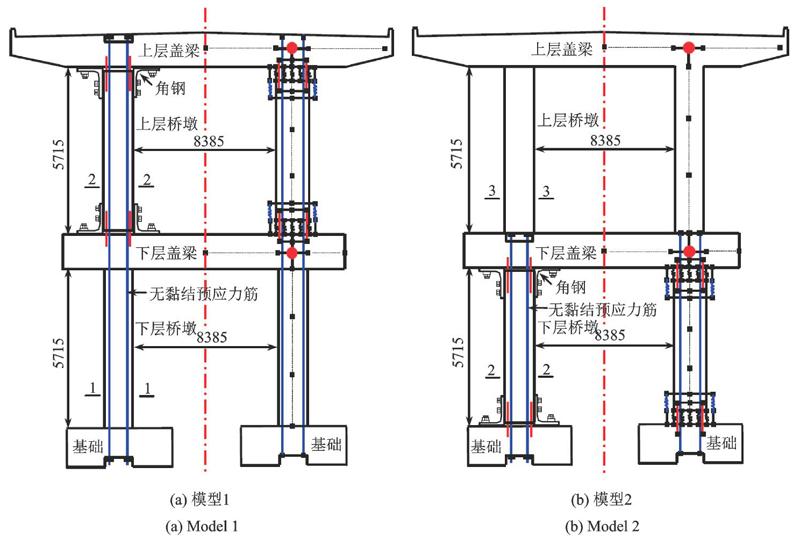
设计了仅上层摇摆、仅下层摇摆以及双层均摇摆3种形式的RSC双层排架墩,本文分别命名为模型1、模型2和模型3。各RSC排架墩尺寸、配筋等设计细节及二维数值分析模型如图1所示。主要由基础、下层桥墩、下层盖梁、上层桥墩、上层盖梁、无黏结预应力筋、角钢、耗能钢筋等组成。另外,在RSC双层排架墩中,发生摇摆反应的桥墩墩顶、墩底位置均设置接缝,接缝位置除无黏结预应力筋及耗能钢筋穿过外,其余钢筋不连续。
图1(a)为模型1设计详图及数值分析模型。模型1的摇摆层设置在上层。上层桥墩墩底、墩顶设置接缝,地震通过接缝的张开和闭合引起上层桥墩发生摇摆反应。下层桥墩墩底、墩顶无接缝,地震中不发生摇摆反应。
图1(b)为模型2设计详图及数值分析模型。模型2的搖摆层设置在下层。下层桥墩的墩顶、墩底设置接缝,上层桥墩墩顶、墩底无接缝。
图1(c)为模型3设计详图及数值分析模型,该模型上层及下层桥墩均可发生摇摆反应。
各模型接缝位置通过设置钢垫板避免强震下混凝土的损伤破坏,并在接缝位置设置耗能钢筋。耗能钢筋起到预制结构施工时的安装定位作用,同时提供一定的耗能能力。模型1、模型2、模型3桥墩中均设置竖向无黏结预应力筋,用于提供结构强震下的自复位及抗倾覆能力。接缝位置设置角钢,用于消耗地震能量且减少桥墩过大的位移反应。
孙治国等[16]完成的试验结果表明,在普通RC桥墩中配置竖向无黏结预应力筋可有效减少桥墩残余位移和混凝土开裂等损伤破坏。考虑到RC桥墩的地震损伤控制设计的要求,模型1下层桥墩亦布置无黏结预应力筋。模型2中,因结构变形集中于下层RSC桥墩,无黏结预应力筋仅穿过下层桥墩。模型3中无黏结预应力筋分别穿过上层桥墩和下层桥墩。
除上述3种RSC双层排架墩外,另设计了1个普通RC双层排架墩(模型4),该排架墩为整体现浇型,不配置无黏结预应力筋,无接缝及角钢。所有桥墩直径均为1015 mm,单层有效墩高均为5715 mm,左右桥墩净间距均为8385 mm。
3种RSC双层排架墩中,摇摆桥墩截面尺寸及配筋情况相同,本文统一命名为2?2截面。该截面配置16根直径22 mm的纵筋,其中8根纵筋在接缝位置截断,剩余8根穿过接缝并在接缝两侧各预留100 mm的无黏结段,作为耗能钢筋。另外,2?2截面中部沿边长700 mm的正方形4个角处各配置了7束Φs15.2无黏结预应力筋,对应预应力筋配筋率为0.48%。
模型1下层桥墩(非摇摆)截面命名为1?1截面,其纵筋及无黏结预应力筋配筋情况与2?2截面相同。唯一的区别在于1?1截面的纵筋在墩顶和墩底位置无截断。
模型2上层桥墩(非摇摆)截面命名为3?3截面,仅配置16根直径22 mm的纵筋。
模型1、模型2和模型3中,无黏结预应力筋初始预应力引起的桥墩轴压比均为0.05。外置角钢截面型号均为L203×203×19。
普通RC双层排架墩(模型4)上下层桥墩截面均配置24根直径32 mm的纵筋。主要是为了保证普通RC双层排架墩配筋率与RSC双层排架墩的总配筋率相当。
2 数值模型建立及验证
建立了3种不同RSC双层排架墩和1个普通RC双层排架墩的二维数值分析模型,并验证了建模方法的准确性。
2.1 材料本构模型
所有桥墩模型中,混凝土抗压强度均为40 MPa,采用OpenSees中的Concrete01材料模型模拟。由于RSC双层排架墩接缝处均设置钢垫板,混凝土不发生破坏,数值模型中此部分混凝土受压应力?应变曲线在峰值荷载后不下降。
纵筋及耗能钢筋屈服强度均为432 MPa,采用各向同性应变硬化的Steel02材料模型模拟。无黏结预应力筋抗拉强度为1860 MPa,选用线弹性的Elastic?PP材料模型模拟。当预应力筋最大应力达到0.8倍抗拉强度时达到条件屈服状态,其提供的自复位能力显著降低,判定预应力筋失效[17]。
为准确模拟接缝处的摇摆反应,采用只受压不受拉的零长度受压弹簧单元模拟。本文中,所有接缝位置均匀布置5个零长度受压弹簧单元,通过各个零长度受压弹簧间的变形差模拟接缝处的反应。该单元的力?变形关系如图2所示,受压刚度E按下面经验公式确定[18]
式中 Ec为桥墩混凝土弹性模量;A为桥墩截面面积;L为墩高的一半;θ为经验系数,本文统一取值2.0。
角钢材料屈服强度为383 MPa,通过零长度角钢弹簧单元模拟,根据Garlock等[19]、蔡小宁等[20]建议的角钢拉压恢复力模型确定关键参数。
角钢的拉压恢复力模型如图3所示,其基本参数确定规则为[19?20]:
1) 由下式计算角钢初始受拉刚度K0
式中 Vap为角钢塑性理论荷载值,ta为角钢厚度。
2)受拉屈服后刚度Kt按下式计算
屈服后角钢的拉力Tax按下式计算
式中 δax为角钢受拉变形。
3) 受拉时的卸载刚度等于初始受拉刚度K0。
4) 反向加载段刚度Kr由d点恢复力Td和c点变形值确定,Td与角钢卸载点的拉力Tb大小相等。
5)角钢受压初始刚度Kc
式中 Ea为角钢材料弹性模量,Aa为角钢竖直肢(与桥墩连接)的截面积;lgh为角钢竖直肢螺栓群中心至水平肢(与盖梁或基础连接)外边缘的距离。
6)角钢在反复拉压下的极限变形δu和极限承载力Tu,即图3中的e点(δu,Tu),参考Shen等[21?22]提出的计算法则:
式中 g1为角钢水平肢螺栓中心至竖直肢外边缘的距离;εu为角钢拉断对应的应变;Tu,Tc分别为角钢能够承受的极限拉力和极限压力,二者大小相等。
2.2 数值分析模型
图1同时展示了各RSC双层排架墩的建模细节。采用纤维梁柱单元模拟桥墩和盖梁。零长度受压弹簧单元由于为零长度,该单元2个节点实际上位于同一位置。对于模型2和模型3下层桥墩与基础接触的部位,位于基础位置的节点和与下层桥墩墩底连接的节点共同组成1个零长度受压弹簧单元。位于基础位置的节点固定,与下层桥墩墩底连接的5个节点之间由刚性单元连接。对于其他接缝位置的零长度受压弹簧单元,建模方法与此类似。
无黏结预应力筋与内置耗能钢筋均采用Truss单元模拟。但无黏结预应力筋采用的是线弹性本构模型,内置耗能纵筋采用弹塑性本构模型。角钢采用零长度角钢弹簧单元模拟。
普通RC双层排架墩(模型4)采用非线性纤维梁柱单元和该单元两端的零长度转动弹簧单元共同模拟。纤维梁柱单元模拟弯曲变形,零长度转动单元模拟纵筋拔出及塑性渗透变形[23]。该建模方法可对弯曲破坏控制的RC结构非线性反应进行准确模拟。
2.3 基于RSC單层排架墩试验结果的验证
选择ElGawady和 Shalan完成的F?FRP1试件拟静力试验结果对本文建模方法进行验证[12]。该试件为RSC单层排架墩,试件尺寸和加载装置以及截面配筋信息分别如图4(a),(b)所示。试验侧向加载采用位移控制。试验加载前,根据桥墩截面的实测材料强度进行弯矩?曲率分析,并根据沿墩高的曲率分布计算得到纵筋首次屈服对应的墩顶屈服位移Δy。然后按Δy的倍数逐级加载,每级位移下循环3次。需要说明的是,Δy的理论计算值未考虑接缝的影响,可能与试验中实际纵筋屈服对应的位移值不一致,但这并不影响对本文数值建模方法准确性的验证。
随着侧向加载位移增大,桥墩上下接缝处张开,如图5所示。图6为模拟与试验滞回曲线的对比,可定性判断模拟得到的试件正负两个方向的强度、负向的刚度等均与试验结果吻合较好。由于试验中正向加载时接缝处局部发生破坏,降低了正向加载的刚度,而数值模型未考虑此破坏,模拟得到的试件正向加载刚度较试验结果偏大。定义滞回环包围的面积为耗能能力,可发现模拟得到的试件耗能能力较试验结果偏小,这是由于试验过程中接缝处垫层的损伤破坏、无黏结预应力筋与周围孔道的摩擦等均会耗能,而数值模型中并未考虑上述因素。但总体来看,模拟与试验滞回曲线拟合较好,验证了本文建模方法的准确性。
3 双层排架墩动力时程分析准备
3.1 双层排架墩基本自振周期
分析得到的4种双层排架墩模型基本自振周期如表1所示。可发现RSC双层排架墩模型的基本自振周期(分别为0.769,0.754和0.892 s)约为普通RC双层排架墩模型的基本自振周期(0.477 s)的1.58?1.87倍。这主要是由于RSC体系的接缝位置混凝土无抗拉强度,且部分纵筋不连续,显著降低了结构的侧向刚度所致。
3.2 地震波的选取
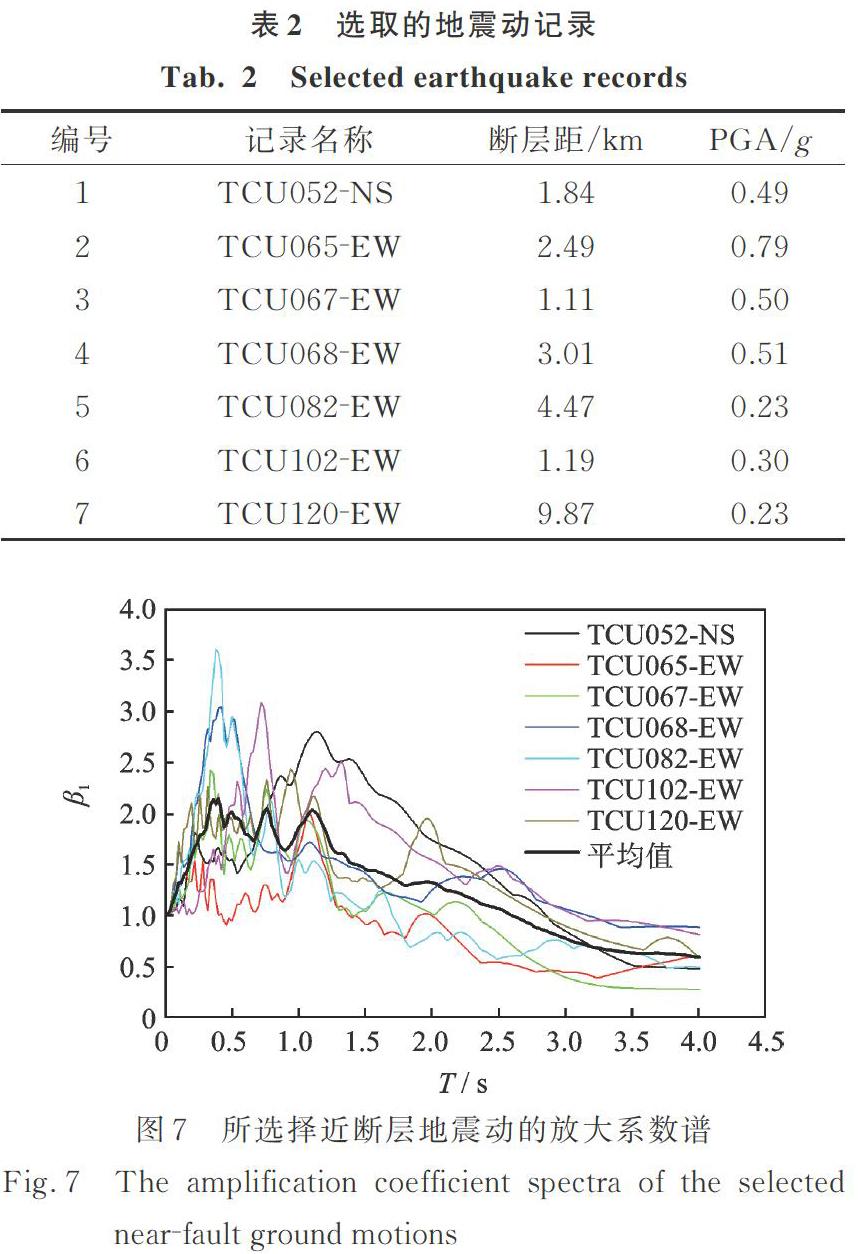
鉴于近断层地震动较远场地震动会给结构输入更高的能量,造成结构更为严重的破坏。以近断层地震动下的反应考察双层桥梁排架墩的抗震性能,是对此类结构抗震能力偏于危险的一种估计。选取7条近断层地震动进行输入,取7条地震动下的反应平均值作为计算结果。需要说明的是,本文的7条近断层地震动均为1999年中国台湾集集地震记录到的。各地震动记录如表2所示,5%阻尼比下各地震动放大系数β1谱如图7所示。数值求解过程中,采用瑞利阻尼,阻尼比为5%,考虑了重力P?Δ效应的影响。另外,由于排架墩横桥向地震危险性更高,本文地震动均沿排架墩横桥向输入。
将地震动的峰值加速度调幅至0.1g和0.4g,其中0.1g代表结构可能遭遇到的中小强度等级的地震,0.4g近断层地震动则代表结构可能遭遇到的较为强烈的地震作用,以研究结构在不同强度地震下的抗震性能。
3.3 RSC双层排架墩失效准则定义
与整体现浇RC结构不同,RSC结构在强震下的变形主要是由接缝的张开引起的,并且由于无黏结预应力筋的存在,RSC结构的地震失效机理不同于传统RC结构。本文定义的RSC双层排架墩失效准则为:
(1) 当排架墩最大层间位移角超过5%时,认为结构失效。这里主要参考了Cheng[11],Thonstad等[14]完成的振动台试验结果。Cheng[11]完成的单层RSC排架墩模型振动台试验,桥墩剪跨比为2.0。结果表明,排架墩层间位移角超过5%时,结构完好。Thonstad等[14]完成的桥梁模型振动台试验,单层RSC排架墩剪跨比在2.5?4.0之间,在超过5%层间位移角时,结构承载力虽有下降,但未倒塌。本文排架墩剪跨比约为2.8,在上述已完成的试验结果范围内。综上,为防止过大的变形下引起结构突然的倒塌,本文以最大层间位移角超过5%作为RSC排架墩失效的界限。
(2) 当桥墩层间残余位移角达到1%时,认为双层排架墩结构失效。这里主要是考虑到普通RC双层排架墩可能因震后层间残余位移角过大而难以修复。RSC双层排架墩由于无黏结预应力筋提供的自复位能力,震后层间残余位移角超过1%的可能性极小。
(3)当无黏结预应力筋的最大应力超过0.8倍抗拉强度后,认为结构失效。此时无黏结预应力筋进入条件屈服状态,接近拉断,已无法保证RSC双层排架墩的自复位能力及抗倾覆能力[24?25]。
4 双层排架墩时程分析结果及对比
4.1 最大层间位移角
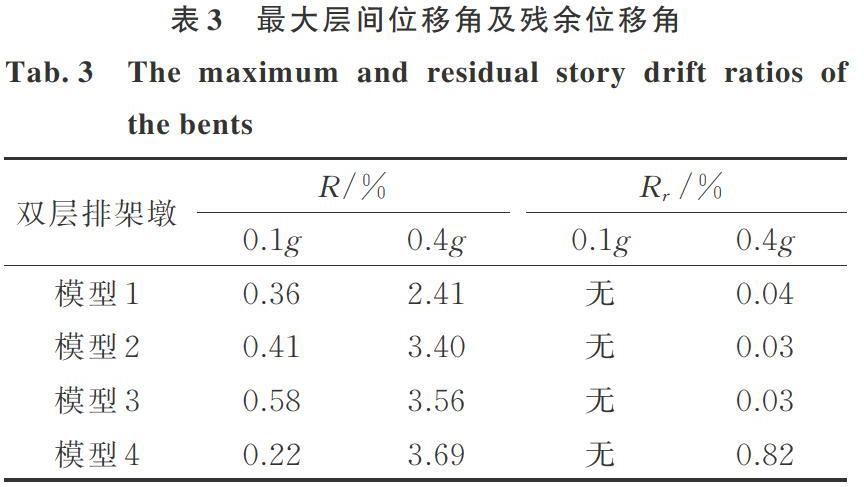
表3为模拟得到的各双层排架墩模型最大层间位移角R值随PGA的变化情况。
当PGA为0.1g时,模型1?模型4的R值分别为0.36%,0.41%,0.58%和0.22%。RSC双层排架墩最大层间位移角约为普通RC双层排架墩的最大层间位移角的1.64?2.64倍。
当PGA增加到0.4g时,模型1?模型4的R值分别增大为2.41%,3.40%,3.56%和3.69%。RSC双层排架墩最大层间位移角约为普通RC双层排架墩最大层间位移角的65.3%?96.5%。
另外,模型2和模型3由于下层桥墩发生摇摆反应,相当于引入了底部薄弱层,0.4g近断层地震动下其最大层间位移角约为模型1最大层间位移角的1.41?1.48倍。
4.2 层间残余位移角
残余位移是指地震动结束后结构不可恢复的变形,它体现了结构震后使用功能快速恢复的能力。表3列出了各双层排架墩的层间残余位移角Rr(%)。
当PGA为0.1g时,4种双层排架墩的Rr值基本为0,主要是由于此时结构基本处于弹性阶段。当PGA为0.4g时,普通RC双层排架墩(模型4)的Rr为0.82%,接近本文定义的1%的失效标准。主要是由于普通RC双层排架墩在强震作用下经历了严重的损伤破坏所致。相比之下,所有RSC双层排架墩的Rr值均很小,模型1的 Rr值最大,也仅为0.04%,可认为几乎无层间残余位移。说明3种RSC双层排架墩均具有良好的自复位能力。
4.3 预应力筋最大应力
表4列出了近断层地震动作用下各RSC双层排架墩中无黏结预应力筋最大应力σmax随PGA的变化情况。
首先,各试件σmax值均随着PGA的增加而增大。PGA为0.1g时,各试件σmax值最大仅为530 MPa。PGA为0.4g时,各试件σmax值分别为936,1198和1247 MPa,约为1860 MPa的50%?67%,小于预应力筋条件屈服应力(本文取1860 MPa的0.8倍,即1490 MPa)。
4.4 角钢受拉变形
角钢为首道抗震防线,其在地震作用下的变形值大小是衡量RSC双层排架墩耗能能力及角钢失效的重要指标。根据Garlock[19]等的试验结果,本文选用角钢受拉屈服及拉断对应的位移分别为1.4,26.0 mm。表4列出了不同PGA下各RSC双层排架墩中角钢的最大变形值δu。
可以发现,在0.1g近断层地震动下,3种模型的角钢最大受拉变形δu(分别为1.45,4.56和7.65 mm)均大于角钢屈服位移,角钢已开始屈服并耗能。在0.4g近断层地震动下,仅下层摇摆的模型2和双层均摇摆的模型3角钢均已拉断。仅上层摇摆的模型1角钢最大变形为8.7 mm,尚未发生拉断破坏。
4.5 曲率延性系数
由于非摇摆层桥墩产生的损伤破坏也会严重影响结构的震后使用功能,本文同时关注了非摇摆层桥墩关键截面的反应情况。
定义桥墩截面在地震动过程中最大曲率与屈服曲率的比值为曲率延性系数,通过曲率延性系数衡量桥墩截面损伤状态。屈服曲率为桥墩截面最外侧纵筋首次屈服对应的曲率值。最大曲率为桥墩截面在地震动输入下的最大曲率反应值,且此时未发生纵筋拉断、混凝土压碎等破坏。一般而言,排架墩墩底承受的弯矩和轴力最大,易发生破坏,本文将模型1下层桥墩墩底、模型2上层桥墩墩底以及模型4下层桥墩墩底定义为关键截面。表5为计算得到的各关键截面的曲率延性系数μφ值随PGA的变化情况。
可以看出,在0.1g近断层地震动作用下,所有截面均未屈服,表示各双层排架墩无明显的损伤破坏。在0.4g近断层地震动作用下,模型4关键截面的曲率延性系数最大,为13.1。模型1和模型2关键截面曲率延性系数分别为5.0和3.6。RSC双层排架墩关键截面曲率延性系数为普通RC双层排架墩关键截面曲率延性系数的27%?38%。说明RSC体系可有效减少强震下双层桥梁排架墩的损伤破坏。
5 结 论
本文设计了仅上层摇摆、仅下层摇摆、上下层均摇摆3种RSC双层排架墩。基于OpenSees结构抗震数值分析平台分别建立了3种RSC双层排架墩及1个普通RC双层排架墩的抗震分析模型,对各模型输入中国台湾集集地震记录到的7条近断层地震动记录,对比分析了各排架墩模型的地震反应,以期为双层桥梁排架墩的地震损伤控制设计提供参考。本文主要结论为:
(1) RSC双层排架墩基本自振周期约为普通RC双层排架墩基本自振周期的1.58?1.87倍。0.4g近断层地震动下,RSC双层排架墩最大层间位移角为普通RC双层排架墩最大层间位移角的65.3%?96.5%。
(2) 在0.4g近断层地震动下,RSC双层排架墩预应力筋最大应力为其抗拉强度的50%?67%,小于预应力筋条件屈服应力。
(3) 在0.4g近断层地震动下,普通RC双层桥梁排架墩层间残余位移角为0.82%,RSC双层排架墩层间残余位移角接近0。
(4) 在0.1g近断层地震动下,RSC双层排架墩中外置角钢已屈服耗能;0.4g近断层地震动下仅上层摇摆的RSC双层排架墩外置角钢未拉断,其余RSC双层排架墩中的角钢均拉断。
(5) 在0.4g近断层地震动下,RSC双层排架墩非摇摆层桥墩关键截面曲率延性系数为普通RC双层排架墩桥墩关键截面曲率延性系数的27%?38%, RSC体系可有效减少双层桥梁排架墩在强震下的损伤破坏。
参 考 文 献:
[1] 彭天波, 李建中, 胡世德, 等. 双层高架桥的抗震性能[J]. 同济大学学报(自然科学版), 2004, 32(10): 1355-1359.
PENG Tianbo, LI Jianzhong, HU Shide, et al. Seismic performance of a double-deck viaduct[J]. Journal of Tongji University (Natural Science), 2004, 32(10): 1355-1359.
[2] 张 洁, 管仲国, 李建中. 双层高架桥梁框架墩抗震性能试验研究[J]. 工程力学, 2017, 34(2): 120-128.
ZHANG Jie, GUAN Zhongguo, LI Jianzhong. Experimental research on seismic performance of frame piers of double-deck viaducts[J]. Engineering Mechanics, 2017, 34(2): 120-128.
[3] 高宗余. 郑州黄河公铁两用桥技术创新[J]. 桥梁建设, 2010, (5): 3-6.
GAO Zongyu. Technical innovations of Zhengzhou Huanghe river rail-cum-road bridge[J]. Bridge Construction, 2010, (5): 3-6.
[4] Kunnath S K, Gross J L. Inelastic response of the cypress viaduct to the Loma Prieta earthquake[J]. Engineering Structures, 1995, 17(7): 485-493.
[5] Marin A, Spacone E. Analysis of reinforced concrete elements including shear effects [J]. ACI Structural Journal, 2016, 103(5): 645-655.
[6] 庄卫林, 刘振宇, 蒋劲松. 汶川大地震公路桥梁震害分析及對策[J]. 岩石力学与工程学报, 2009, 28(7): 1377-1387.
ZHUANG Weilin, LIU Zhenyu, JIANG Jinsong. Earthquake-induced damage analysis of highway bridges in Wenchuan earthquake and countermeasures [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1377-1387.
[7] 李建中, 管仲國. 桥梁抗震设计理论发展:从结构抗震减震到震后可恢复设计[J]. 中国公路学报, 2017, 30(12): 1-9.
LI Jianzhong, GUAN Zhongguo. Research progress on bridge seismic design: Target from seismic alleviation to post-earthquake structural resilience [J]. China Journal of Highway and Transport, 2017, 30(12): 1-9.
[8] 韩 强, 贾振雷, 何维利, 等. 自复位双柱式摇摆桥梁抗震设计方法及工程应用[J]. 中国公路学报, 2017, 30(12): 169-177.
HAN Qiang, JIA Zhenlei, HE Weili, et al. Seismic design method and its engineering application of self-centering double-column rocking bridge [J]. China Journal of Highway and Transport, 2017, 30(12): 169-177.
[9] 王志强, 卫张震, 魏红一, 等. 预制拼装联结件形式对桥墩抗震性能的影响[J]. 中国公路学报, 2017, 30(5): 74-80.
WANG Zhiqiang, WEI Zhangzhen, WEI Hongyi, et al. Influence of precast segmental connector forms on seismic performance of bridge pier [J]. China Journal of Highway and Transport, 2017, 30(5): 74-80.
[10] Marriot D, Pampanin S, Palermo A. Biaxial testing of unbonded post-tensioned rocking bridge piers with external replaceable dissipaters [J]. Earthquake Engineering and Structural Dynamics, 2011, 40(15): 1723-1741.
[11] Cheng C T. Shaking table test of a self-centering designed bridge substructure [J]. Engineering Structures, 2008, 30(12):3426-3433.
[12] ElGawady M A, Shalan A. Seismic behavior of self-centering precast segmental bridge bents [J]. Journal of Bridge Engineering, ASCE, 2011, 16(3): 328-339.
[13] 孙治国, 谷明洋, 司炳君. 外置角钢摇摆-自复位双柱墩抗震性能分析[J]. 中国公路学报, 2017, 30(12): 40-49.
SUN Zhiguo, GU Mingyang, SI Bingjun. Seismic behavior analyses of rocking self-centering double column bridge bents using external angles [J]. China Journal of Highway and Transport, 2017, 30(12): 40-49.
[14] Thonstad T, Mantawy I M, Stanton J F, et al. Shaking table performance of a new bridge system with pretensioned rocking columns [J]. Journal of Bridge Engineering, ASCE, 2016, 21(4): 04015079.
[15] Han Q, Jia Z, Xu K, et al. Hysteretic behavior investigation of self-centering double-column rocking piers for seismic resilience[J]. Engineering Structures, 2019, 188: 218-232.
[16] 孙治国, 王东升, 司炳君, 等. 采用预应力筋进行RC桥墩地震损伤控制的试验研究[J]. 土木工程学报, 2014, 47(1) :107-116.
SUN Zhiguo, WANG Dongsheng, SI Bingjun, et al. Experimental research on the seismic damage control techniques for RC bridge piers by using prestressing tendons[J]. China Civil Engineering Journal, 2014, 47(1) :107-116.
[17] Yamashita R, Sander D H. Seismic performance of precast unbonded prestressed concrete columns [J]. ACI Structural Journal, 2009, 106(6): 821-830.
[18] 司炳君, 谷明洋, 孙治国, 等. 近断层地震动下摇摆―自复位桥墩地震反应分析[J].工程力学,2017, 34(10):87-97.
SI Bingjun, GU Mingyang, SUN Zhiguo, et al. Seismic response analysis of the rocking self-centering bridge piers under the near-fault ground motions[J]. Engineering Mechanics, 2017, 34(10):87-97.
[19] Garlock M M, Ricles J M, Sause R. Cyclic load tests and analysis of bolted top-and-seat angle connections [J]. Journal of Structural Engineering, ASCE, 2003, 129(12): 1614-1625.
[20] 蔡小寧, 孟少平, 孙巍巍, 等. 顶底角钢连接半刚性钢结构抗震性能数值分析[J]. 工程力学, 2012, 29(7): 124-129.
CAI Xiaoning, MENG Shaoping, SUN Weiwei,et al. Numerical analysis for seismic behavior of semi-rigid steel beam-to-column connection with top-and-seat angles [J]. Engineering Mechanics, 2012, 29(7): 124-129.
[21] Shen J, Astaneh-asl A. Hysteretic behavior of bolted-angle connections [J]. Journal of Constructional Steel Research, 1999, 51(3): 201-218.
[22] Shen J, Astaneh-asl A. Hysteresis model of bolted-angle Connections [J]. Journal of Constructional Steel Research, 2000, 54(3): 317-343.
[23] 孙治国, 华承俊, 司炳君, 等. 设置延性系梁的桥梁双柱墩抗震能力研究[J]. 桥梁建设, 2015, 45(1): 39-44.
SUN Zhiguo, HUA Chengjun, SI Bingjun, et al. Study of seismic resistance capacity of double-column bridge pier arranged with ductile tie beam[J]. Bridge Construction, 2015, 45(1): 39-44.
[24] 孙治国, 赵泰儀, 王东升, 等.基于RSC体系的双层桥梁排架墩地震损伤控制设计[J]. 中国公路学报, 2020, 33(3): 97-106.
SUN Zhiguo, ZHAO Taiyi, WANG Dongsheng, et al. Seismic damage control design for double-deck bridge bents based on rocking self-centering system[J]. China Journal of Highway and Transport, 2020, 33(3): 97-106.
[25] 赵泰儀. 摇摆-自复位双层桥梁排架墩抗震性能分析[D]. 大连: 大连海事大学, 2019.
作者简介: 孙治国(1980?),男,博士,副研究员。电话:18941134800;E-mail:sunzhiguo@cidp.edu.cn

