类比推理 一脉相通

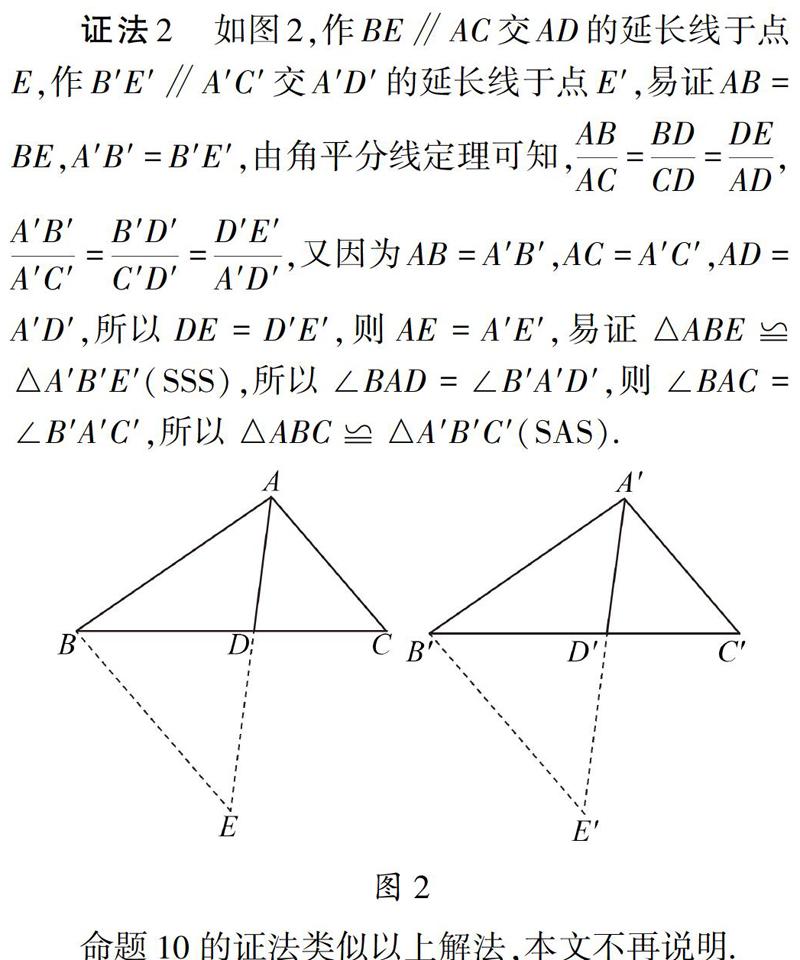
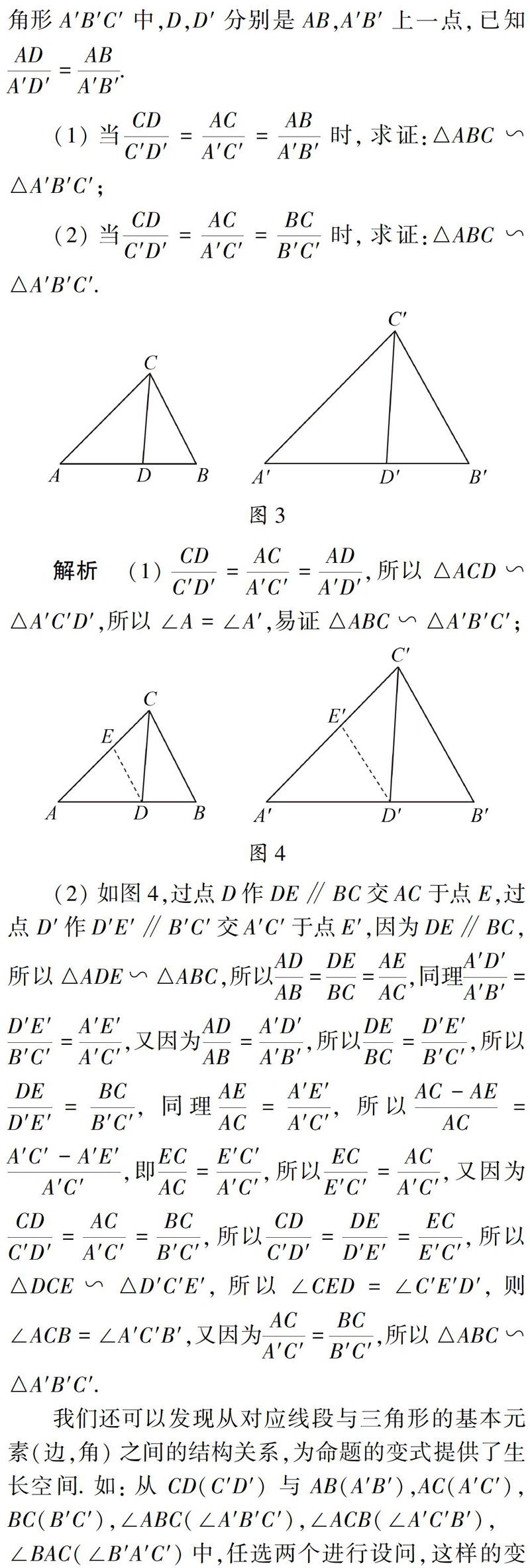
【摘 要】 從课本上的一个“全等”习题出发，借助类比推理，在复习时让学生的思维在“全等”与“相似”之间跳跃，这样丰富了想象力与创造力，帮助学生建立，拓展和完善了知识结构，使知识网络化，系统化.

【关键词】 全等，相似，类比，串联

美国数学家哈尔莫斯指出：“定理、证明、概念、定义、理论、公式、方法中的任何一个都不是数学的心脏，只有问题才是数学的心脏”.数学的思维是解决问题的心智活动，可以引导学生不断深入思考，再创造，从深层次，多角度思考问题.本文从课本上的一道“全等”习题出发，借助类比推理，让学生的思维在“全等”与“相似”之间跳跃，这样极大地丰富了想象力与创造力，帮助学生建立、完善和拓展知识结构，实现知识的再认、再现、再建，培育创新思维[1].

1 类比联想

1.1 原题呈现，等闲识得东风面

命题1 （人教版8上课本第56页第13题）有两边和其中一边上的中线对应相等的两个三角形全等.

命题2 有两边和第三边上的中线对应相等的两个三角形全等.

1.2 改变条件，一花引来百花开

将命题中的“中线”分别类比替换成“角平分线”，“高”得到以下真命题：

命题3 有两角和其中一角的角平分线对应相等的两个三角形全等.

命题4 有两角和第三个角的角平分线对应相等的两个三角形全等.

命题5 有两边和其中一边上的高对应相等的两个锐角三角形全等.

命题6 有两边和第三边上的高对应相等的两个锐角三角形全等.

上述命题，全面系统复习了全等三角形的判定和性质.

1.3 弱化条件，映日荷花别样红

将上述命题5、命题6中的锐角三角形中的“锐角”去掉，得到以下两个命题：

还可从基本元素（边，角）与相关元素所给出的数量关系或位置关系等条件，进行整体图形关系的探究，类似的变式，此处不再一一说明，由此可以看出，“全等”是特殊的“相似”，“相似”是一般化的“全等”[3]，在判断“全等”的路途上，利用“全等”的活动经验和辅助线的做法，可得到“相似”的类比结论.还可将文中命题11，命题12中的“两个同为锐角（或同为钝角）的三角形”去掉，因此问题就类似于本文命题7，命题8，是否相似需要讨论，探讨从“全等”到“相似”的变与不变，凸显数学的美[3].

4 教学思考

4.1 融入科学训练，获得类比体验

类比是将已有知识与新的学习活动联系起来的一种重要方式[4].在教学实践中，教师可引导学生根据现有的知识经验，将新知识与熟悉的旧知识进行类比，轻松发现新问题，如：我们还可以引导学生从“相似三角形的周长比等于相似比，面积比等于相似比的平方”入手，找寻相应的逆命题，再判断其真假性.类比是学生建立、拓展和完善数学知识的一种基本方法.类比有利于搭建新旧知识之间的桥梁，找出新旧知识之间的联系，把握它们的异同，逐步建立良好的知识结构，把知识各个部分、因素、层次的认知结合起来，加深对知识的理解，提升学生的迁移能力.同时类比还是一种有效的记忆方式，通过归纳、类比、联想可以提高学生的记忆效果，真正减轻学生的负担.

4.2 精心组织学材，培养核心素养

在教学中，我们要理解数学教学，把握问题本质，深入挖掘数学问题的教育价值，既要优化解题思路，又要借题发挥，对问题进行变式、延伸与拓展.习题教学中要设置好问题串，设计好问题与问题之间的关联，通过有层次、有梯度的问题“串联”，如：命题1～8在八年级即可解决，命题9～12命题则在九年级复习中串起命题1～8，通过横向和纵向迁移，在展示数学逻辑思维结构的过程中，培养学生学会提出问题、分析问题、解决问题的能力，将类比、归纳、数形结合等思想方法，内化为自己研究数学的手段，生长出思维链.

参考文献

[1]陈浩.问题链中的意外插曲[J].中学数学，2007（3）.

[2]童浩军.全等三角形判定中的几个拓展命题[J].中小学数学，2007（1-2）.

[3]康叶红.聚焦几何证明，凸显核心素养[J].中学数学教学参考（中旬），2020（11）.

[4]钱佩玲，邵光华.数学思想方法与中心数学[M].北京：北京师范大学出版社，2012.

作者简介 陈浩（1975—），男，湖北武汉人，中学高级教师，学科带头人，武汉市陈浩数学教学研究室主持人，曾在各级报刊杂志发表文章80余篇.