地震作用下型钢混凝土异形柱框架动力特性及频谱反应分析

胡宗波 薛建阳

摘要： 基于型钢混凝土（SRC）异形柱空间框架模型振动台试验，对模型结构的频谱特性、偏心动力反应、非线性反应规律进行了研究。结果表明：在三向地震作用下，模型结构在高阶振型中依次发生了Y向平扭和X向平扭耦合现象，振型形态依次为X向平动、Y向平扭、Z向振动、扭转、Y向平动;在强震作用下，模型X向、Y向、Z向和扭转自振频率分别下降31.02%，30.10%，39.72%和30.09%;模型结构的频响函数实部曲线的零点、虚部及幅值曲线的峰值点随着加载持时的增加逐渐向低频移动，结构损伤逐渐累积，刚度不断退化，动力刚度接近静刚度，结构的变形较大;通过数值分析可知，当偏心距一定、平扭周期比不变时，偏心结构的自振频率比、平扭耦联系数的峰值点相对于对称结构的峰值点明显推后;在强震作用下，偏心距小于0.1的模型结构的薄弱层出现在结构中下部，偏心距大于0.3的模型结构的薄弱层出现在结构上部;随着偏心距的增大，模型结构提前达到性能点，所有交点处的能力谱曲线未处于承载力明显下降段，结构抗震性能满足要求。

关键词： 型钢混凝土异形柱; 框架结构; 动力特性; 频谱分析; 非线性分析

中图分类号： TU398+.7; TU311.3    文献标志码： A    文章编号： 1004-4523（2021）03-0528-11

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.010

引  言

在动力作用下，结构的振动特性，称为结构的自振特性。分析结构的动力特性是进行结构抗震设计和结构损伤分析的重要步骤[1]。对于型钢混凝土（Steel Reinforced Concrete，SRC）异形柱框架这一新型结构体系，已有的研究多集中在中国[2?5]，且仅针对SRC异形柱构件或平面框架进行了拟静力或拟动力试验研究[6?7]，缺少对SRC异形柱结构体系动力特性的认识。尤其是在三向地震作用下，SRC异形柱空间框架结构的地震反应较为复杂，当结构进入弹塑性阶段后，结构刚度的退化、塑性铰的分布、各抗侧构件屈服位移的不同都将影响结构的弹塑性反应[8]。由于结构的刚心和频率比不断随时间变化，SRC异形柱框架结构的动力扭转作用明显，从而影响结构的频谱特性和动力反应。

为准确掌握SRC异形柱框架结构的动力特性及弹塑性反应规律，课题组采用振动台试验、数值计算、非线性静力分析的方法，对模型结构的动力特性和频谱反应进行研究，为型钢混凝土异形柱结构的抗震设计提供理论参考。

1 试验概况

1.1 振动台试验

为获取型钢混凝土异形柱框架在三向地震作用下的位移反应、加速度反应和应变反应，课题组按照1∶4的相似比，根据动力相似关系，设计了一栋5层实腹式型钢混凝土异形柱空间框架结构模型，如图1所示。模型结构平面对称布置，结构抗侧力构件为L形、T形、十形等肢型钢混凝土异形柱，如图2所示。柱型钢采用Q235钢，受力筋采用HPB300级钢筋，箍筋采用10#3.0镀锌铁丝，混凝土采用C30微粒混凝土。

试验选用El Centro波、Taft波和兰州人工波作为台面激励波形，按1∶0.67相似比调整台面输入加速度峰值，调整后的工况共60个（包括白噪声），加速度峰值分别为0.07g，0.14g，0.20g，0.40g，0.62g，0.80g，0.90g，1.0g和1.1g。同一地震等级试验中，按1∶2相似比调整时间间隔，各地震波依次单向输入、双向输入、三向输入;X，Y和Z三向加速度比值为1∶0.85∶0.65。试验中采用加速度计、位移拾振器、应变传感器量测模型结构的动力响应，测点布置如图3所示。具体试验参数及详细试验过程见文献[9]。

1.2 试验结果

由于El Centro波作用下的结构反应强于Taft波及兰州人工波，因此选用El Centro波作为典型分析波形。图4和5所示为模型顶层X向、Y向、Z向加速度响应和位移响应。

在地震波持续作用下，模型结构反应分为三个阶段。0.20g前为弹性阶段。0.40g?0.80g为弹塑性阶段。此阶段，一层A1轴和C3轴L形角柱上柱端翼缘出现细长裂缝，一层C1轴、A3轴边框架梁端裂缝向上、向下发展，其他梁端不同程度出现微小斜裂缝（如图6（a）所示）;A1轴和C3轴L形角柱腹板由上至下均匀出现不等长多条水平裂缝（如图6（b）所示）;三层A3轴L形角柱与梁连接处产生45°斜裂缝，三层A3轴边框架梁端钢筋压应变达到量测极限。0.90g后为塑性阶段。此阶段，一层B1轴T形边柱与梁相交处出现向节点发展的微裂缝（如图6（c）所示）;三层A3轴L形角柱与梁连接处形成交叉裂缝;一层、二层A1，A3，C1，C3轴L形角柱柱跟裂缝贯通（如图6（d）所示）;1.0g后，一至三层角柱和边柱与梁连接处裂缝相交贯通;三层A3轴边框架梁端钢筋出现应力失效。

2 结构动力特性分析

2.1 自振频率分析

通过对模型结构进行白噪声扫频，得到模型结构各层的加速度反应信号，然后以底座上的加速度信号作为激励信号，以各楼层上的加速度信号作为输出信号，对激励信号和输出信号采用频域分析方法得到各层的频响函数即传递函数，利用传递函数可做出模型的幅频曲线和相频曲线，幅频曲线峰值所对应的频率值依次为模型结构的各阶次自振频率。图7列出了历次白噪声输入后，模型结构顶层测点（A12）相对基底臺面（A7）的X方向加速度幅频曲线;图8列出了模型结构顶层测点（AY6）相对基底台面（AY1）的Y方向加速度幅频曲线;图9列出了模型结构顶层测点（AZ7）相对基底台面（AZ1）竖向加速度幅频曲线;图10列出了模型结构顶层测点（AY7?AY11）相对基底台面（AY1）的扭转幅频曲线;图11列出了模型结构平?扭耦合频率的分布情况。

通过对模型结构的幅频曲线分析可知：模型结构的平动2阶频率约为1阶频率的4倍，竖向振动2阶频率约为1阶频率的3.5倍，模型结构的扭转幅度在各阶自振频率附近急剧增大，在其他频率点上，曲线幅值变化平缓;随着地震输入加速度峰值的增加，模型结构各阶频率值逐渐前移，模型X向、Y向、Z向和扭转自振频率均呈下降趋势，模型结构在高阶振型中依次发生了Y向平扭和X向平扭耦合现象。结合试验过程发现，在输入0.07g加速度峰值地震波后，模型X向、Y向、Z向和扭转自振频率与加载前相比变化不大，可以认为结构处于弹性阶段;在输入0.20g加速度峰值地震波后，结构自振频率开始缓慢下降，且X向下降幅度较Y向大，Z向下降幅度与X向较接近，扭转3阶频率下降幅度最大，此时，异形柱构件开始出现少量斜向裂缝;在输入0.40g加速度峰值地震波后，模型自振频率迅速下降，其X向、Y向1阶和2阶频率较震前分别下降18.18%，19.42%和18.95%，12.61%，Z向、扭转1阶和2阶频率较震前分别下降23.60%，19.02%和16.01%，18.31%，模型梁柱裂缝展开迅速，结构破坏程度显著加剧;最后依次输入加速度峰值为0.8g，0.9g，1.0g的地震作用后，模型X向、Y向、Z向和扭转自振频率缓慢降低;试验结束后模型X向、Y向、Z向和扭转自振频率分别下降31.02%，30.10%，39.72%，30.09%，整体刚度仅为震前的45.43%和47.36%，结构破坏较为严重。

2.2 阻尼比分析

模型结构的阻尼比由传递函数曲线根据半功率法求得，如图12所示，它反映了结构的耗能特性。试验前通过白噪声扫描得到模型平动阻尼比约为0.037、XY平面转动方向的阻尼比约为0.012。试验过程中，阻尼比随着地震强度的增加而逐渐增大，尤其是自振周期超过0.18 s时，模型进入弹塑性状态，阻尼比陡然提升，阻尼比增大的幅度相对于试验前期阶段较为明显。试验结束时，模型X方向的阻尼比约为0.18、Y方向约为0.11、Z方向约为0.222、XY平面转动方向约为0.231，这主要是由于结构累积损伤程度增大而导致耗能的提高。

2.3 振型分析

模型结构的振动形态由传递函数曲线求得，利用传递函数可作出模型各层相对于基底台面的幅频曲线和相频曲线，同时计算各层加速度幅频曲线中同一自振频率处的幅值比，结合相频曲线判断其相位，并经归一化处理后，可得到该自振频率对应的振型。图13为模型在水平向前2阶平动振型;图14为模型XY平面扭转前2阶振型。

通过对模型结构的振型曲线分析可知：模型结构平动主振型为“剪切平动”，扭转主振型为“剪切扭转”，在整个试验过程中，模型在不同试验阶段的振动特性都以基本振型为主;在高阶振型中，模型结构4层、5层为负振幅，结构层间受到拉力作用，此时模型结构受竖向地震作用较为明显;模型XY平面扭转主振型表现为结构各层绕平面法线方向作同向相对旋转，从而引起楼层在X方向、Y方向产生水平位移，使得异形柱构件承受由楼层扭矩分配的剪力和平动产生的剪力的共同作用;当多次输入较高峰值加速度地震波以后，由于底层承受的水平剪力和扭矩较大，柱混凝土出现剪切斜裂缝，1层?2层柱损伤累积效果显现，试验后期，1层?3层的梁柱斜裂缝增多，模型刚度明显退化。

按照振型反应谱法，考虑平扭耦合的影响，将分解后的单一振型按照频率大小进行排序可得到模型结构的主振型。SRC异形柱框架结构模型在三向地震作用下的自振频率、阻尼比、振型分布如表1所示。

3 结构振动反应频域分析

3.1 频响函数分析

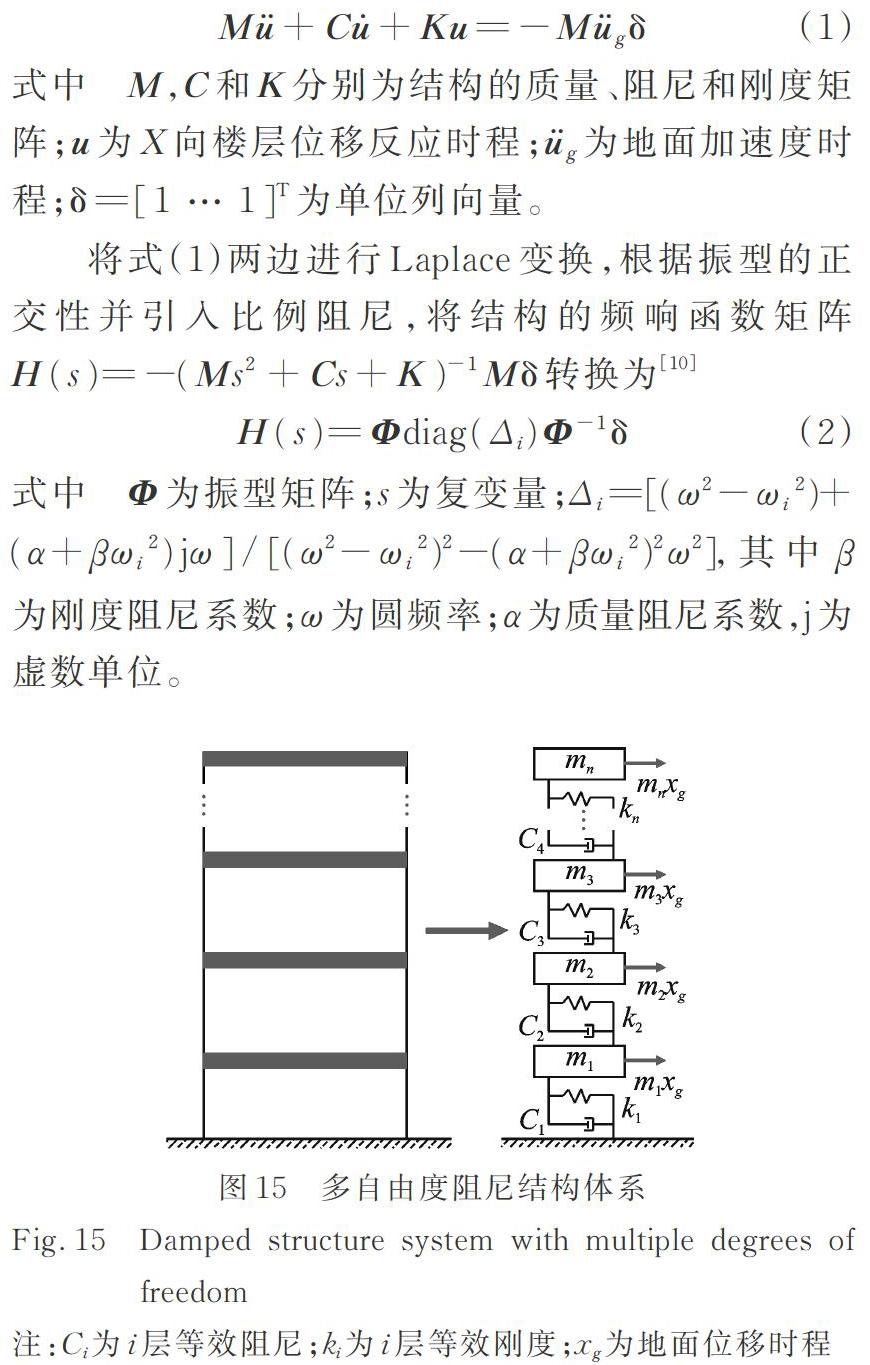
根据SRC异形柱框架结构在水平地震作用下的振动形态，将多层SRC异形柱框架结构简化为具有多个自由度的阻尼剪切型结构，如图15所示。运动方程为

式中  ，和分别为结构的质量、阻尼和刚度矩阵;u为X向楼层位移反应时程;为地面加速度时程;为单位列向量。

将式（1）两边进行Laplace变换，根据振型的正交性并引入比例阻尼，将结构的频响函数矩阵转换为[10]

根据式（2），对模型振动台基座和试验模型顶层采集到的位移信号进行Laplace变换，可得到试验模型的频响函数曲线。图16给出了模型在不同工况下结构X向的频响函数实部、虚部及幅值曲线。随着加载持时的增加，实部曲线的零点、虚部及幅值曲线的峰值点逐渐向低频移动，这说明持续加载导致结构损伤逐渐累积，刚度不断退化，自振频率不断降低。尽管结构的频响函数曲线的差异逐渐增大，但总体形状基本一致。依据上述方法，同理可得结构Y向的频响函数实部、虚部及幅值曲线，其变化特征与X向相同。

为方便观察，运用MATLAB将频响函数曲线进行标准化（纵坐标最大值定义为1，其他依次呈比例取值）处理[11]。图17给出了结构在1WN至57WN工况下的1阶标准化自振频率|ω0|的变化情况。从图中可以看出，随着加载持时的增加，结构的1阶自振频率整体呈下降趋势，反映了结构损伤不断累积及刚度不断退化的现象。

3.2 偏心距的動力影响分析

将式（1）运动方程中的位移向量引入偏心转角分量，地震加速度向量引入转动分量。为简化计算，当仅考虑X向主振方向地震作用和Y向偏心时，求解特征方程。

则偏心结构自振频率表达式为

式中  ，Tφe/Tu为仅考虑偏心影响的非耦联平扭周期比;Tφt/Tu为地面转动引起的平扭周期比。

结构的扭转效应用相对扭转效应指标φr/u来评判，其中φ，r分别为楼层的扭转角和回转半径，u为质心位移，φr为扭转产生的楼层水平相对位移，可反映结构扭转效应相对平动反应的关系。因此，当周期处于反应谱下降段时，组合后的可表示为

结构1阶、2阶自振频率比ω1/ω2的变化规律如图18所示。由图18（a）可知：当偏心扭转的平扭周期比Tφe/Tu<0.75时，结构1阶、2阶自振频率之比ω1/ω2随着平扭周期比Tφe/Tu的增加而增大;当Tφt/Tu≥2.0且Tφe/Tu=0.8，Tφt/Tu≤1.0且Tφe/Tu=1.25时，结构1阶、2阶自振频率之比ω1/ω2出现峰值点，之后，结构1阶、2阶自振频率之比ω1/ω2逐渐减小，减小幅度随着平扭周期比的增加逐渐减弱;当Tφt/Tu≥2.0时，趋于稳定。由图18（b）可知：当偏心距ey/r一定、地面转动引起的平扭周期比Tφt/Tu不变时，考虑地面转动影响的结构自振频率比的峰值点相对于仅考虑偏心影响的峰值点明显推后。

结构振型中考虑地面转动影响的扭转分量与平移分量振幅比的变化规律如图19所示，在非耦联平扭周期比Tφe/Tu=1处，相对扭转效应出现了明显的峰值点，说明当Tφe/Tu≤1时，因平扭联合产生的水平位移增加幅度小于扭转角的增加幅度，反之，平扭联合产生的水平位移增加幅度大于扭转角的增加幅度，因而出现了下降趋势。SRC异形柱框架结构Y向平扭耦联的理论扭转效应与试验值对比如图20所示。SRC异形柱框架结构在三向地震作用下，底层最大扭转位移与Y向水平位移之比最大值为0.0007，SRC异形柱空间对称框架结构的Y向偶然相对偏心距<0.1。

4 结构非线性反应谱分析

4.1 平扭振动反应分析

通过上述理论分析和振动台试验发现，由于在地震作用下模型结构的刚心、平扭周期比和频率比不断随时间变化，SRC异形柱框架结构的动力扭转作用明显，从而影响结构的频谱特性和动力反应。因此，有必要在振动台试验的基础上，深入对SRC异形柱空间框架结构的平?扭反应规律进行分析。本节利用OpenSees平台采用基于有限元柔度法的纤维模型梁柱单元[12]，对不同偏心距的SRC异形柱空间框架结构的平?扭耦联弹塑性反应规律进行研究。

图21和22分别列出了模型顶层X向、Y向扭转角反应时程曲线。由图可知：在双向地震作用下，等距双向偏心结构的X向、Y向扭转角反应规律相近，但Y向扭转角反应相对较大，这说明模型结构的Y向平扭耦联反应较为明显，这与振动台试验得到的规律一致;对于偏心结构，随着地震动强度的增加，层间扭转角逐渐增大，并伴随着偏心距的增加不断增大，且Y向的增大幅度显然比X向大;当地震输入波加速度峰值amax≥0.62g时，随着偏心距的增大，模型顶层扭转角时程曲线的中心线逐渐发生偏移，并且不断向上发展，这是由于偏心距过大，楼层的转动轴发生了水平移动所引起的，这时模型结构已进入塑性扭转阶段。

4.2 延性性能分析

利用OpenSees非线性静力分析功能，对4个不同偏心距的SRC异形柱空间框架结构模型进行推覆模拟，通过结构的能力谱和地震需求谱来直接估计结构的弹塑性反应[13]。推覆模拟加载方式采用单调增加水平荷载作用，按照振型分解反应谱法计算模型各层的层间剪力，通过楼层层间剪力计算各层水平荷载，作为下一加载步的水平荷载分布形式，目标位移设为动力时程分析时结构顶点平均位移的1.4倍。通过推覆模拟，得到了不同偏心距模型的基底剪力?顶点位移曲线，如图23所示。图中，，分别表示偏心距e/l=1.0的模型结构顶点屈服位移和极限位移，其他同类标注含义相同。

由图可知：相对偏心距e/l为0.1，0.3，0.5，1.0时，模型结构的屈服位移分别为112.97，88.65，77.87，43.67 mm。在弹性阶段，即基底剪力达到最大值前，受偏心扭转贡献的楼层剪力增量的影响，同一顶点位移处，偏心距越大模型基底承担的剪力越大;随着偏心距的增大，结构基底剪力达到最大值时的顶点位移不断提前。当基底剪力达到最大值后，模型结构即刻进入塑性阶段，基底剪力陡降，随着偏心距的增加降幅越大;当位移控制达到动力时程分析时结构顶点平均位移的1.4倍，模型结构没有丧失承载力而倒塌，位移值仍在增大，这说明型钢混凝土异形柱框架结构具有较好的延性，偏心距越小延性越好，反之越差。

由于SRC异形柱框架模型结构的刚度较大，在进行模拟推覆分析时，其弹塑性阶段不明显，因此在确定模型屈服位移和极限位移时采用两阶段线性化折线模型。即：假定在基底剪力达到最大值前，模型结构均处于弹性阶段，过了剪力最大值这个临界点后，模型结构立即进入塑性状态，基底剪力随之下降，基底剪力降低85%时所对应的位移即为模型结构的极限位移。其延性系数的计算方法与拟静力试验方法原理相同，图24列出了模型结构的延性系数。由图可知：相对偏心距e/l为0.1，0.3，0.5和1.0时，模型结构的延性系数分别为3.56，1.58，1.42，1.29。这说明当e/l≤0.1时，模型结构的延性较好，其延性系数随偏心距的增加不断降低，其塑性变形能力随偏心距的增加不断降低，降低幅度随偏心距的增加不断减小。

4.3 能力谱分析

弹塑性需求谱采用ATC?40中的方法确定[14]。将规范反应谱和Pushover曲线转换为谱加速度（Sa）?谱位移（Sd）曲线，形成能力谱和需求谱绘于图25中。SRA，SRV分别代表加速度谱和速度谱直线段的折减系数，aA为反应谱平台段加速度峰值，aV为反应谱下阶段速度峰值。从图中可以看出：不同偏心距模型的能力谱曲线与弹塑性需求谱均有交点，但是交点位置不同，随着偏心距的增加交点位置更加提前，这说明大偏心距的模型结构更早达到性能点，这对结构抗震是较为不利的;所有交点处的能力曲线未处于承载力明显下降段，结构抗震性能满足要求，当偏心距e/l≥0.3时，模型的能力需求曲线下降较陡，随着顶点位移不断加大，其失效的可能性也较大。

4.4 性能点分析

能力谱法的抗震性能评价标准是：在结构性能点处，其层间位移角满足规范要求时说明结构能够抵御相应等级的地震作用，否则说明结构的抗震能力不足。按Sa?Sd转换方法，得到不同偏心距模型结构性能点位置的顶点位移如表2所示。不同偏心距模型结构在性能点状态下的层间位移角如表3所示。

由表2和3可知：在结构性能点处，模型结构的顶点位移随偏心距的增加不断减小，其减小幅度不断降低;当偏心距e/l≤0.1时，小偏心距对结构的扭转效应影响有限，地震动强度是影响层间位移的主要因素，其最大层间位移角出现在2层，约为1/25;当偏心距e/l≥0.3时，各模型层间位移角的变化趋势很接近，且层间位移角的最大值出现在顶层，约为1/12，这说明当偏心距e/l≥0.3时，模型结构的扭转反应剧烈，由偏心扭转引起的层间位移增量较大。

图26列出了不同偏心距模型结构在Pushover分析达到目标位移时的层间位移角分布情况。由图可知：在强震作用下，当0.1≤e/l<0.3时，模型1层、2层、3层的层间最大位移角大于1/25;当e/l≥0.3时，模型结构的顶层最大层间位移角大于1/12，超過规范规定的弹塑性层间位移角允许值[1/50]。这说明，在强震作用下，小偏心距SRC异形柱结构模型的薄弱层出现在结构中下部，大偏心距SRC异形柱结构模型的薄弱层出现在结构上部。

5 結  论

基于振动台试验和数值分析，对SRC异形柱框架结构的动力特性和频谱反应进行分析，结论如下：

（1）模型结构在高阶振型中依次发生了Y向平扭和X向平扭耦合现象，在强震作用下，模型X向、Y向、Z向和扭转自振频率分别下降31.02%，30.10%，39.72%和30.09%，整体刚度仅为震前的45.43%和47.36%。

（2）模型结构的频响函数实部曲线的零点、虚部及幅值曲线的峰值点随着加载持时的增加，逐渐向低频移动，结构损伤逐渐累积，刚度不断退化，自振频率不断降低。

（3）模型结构的自振频率是相对偏心距ey/r、地面转动引起的平扭周期比Tφt/Tu、仅考虑偏心扭转的平扭周期比Tφe/Tu的函数。当偏心距ey/r一定、平扭周期比Tφt/Tu不变时，偏心结构的自振频率比、平扭耦联系数的峰值点相对于对称结构的峰值点明显推后;在Tφe/Tu>1.0以后，扭转振幅有明显的放大现象，1阶振型的参与程度较高。

（4）模型结构在偏心距e/l=0.1时的延性系数为3.56，e/l≥0.3时的延性系数小于1.5;在强震作用下，偏心距e/l≤0.1的SRC异形柱结构模型的薄弱层出现在结构中下部，偏心距e/l≥0.3的SRC异形柱结构模型的薄弱层出现在结构上部。随着偏心距的增大，模型结构提前达到性能点，所有交点处的能力谱曲线未处于承载力明显下降段，结构抗震性能满足要求。

参考文献：

[1] 龚炳年， 郝锐坤， 赵宁. 钢-混凝土混合结构模型动力特性的试验研究[J]. 建筑结构学报， 1995， 16（3）： 37-43.

Gong Bingnian， Hao Ruikun， Zhao Ning. Experimental investigations of the dynamic characteristics of a 23-storey steel-RC mixed structure model[J]. Journal of Building Structures， 1995， 16（3）： 37-43.

[2] Hsu Cheng-Tzu Thomas. T-shaped reinforced concrete members under biaxial bending and axial compression[J]. ACI Structure Journal， 1989， 86（4）： 460-468.

[3] Tokgoz S， Dundar C. Test of eccentrically loaded L-shaped section steel fibre high strength reinforced concrete and composite columns[J]. Engineering Structure， 2012， 38（5）： 134-141.

[4] 薛建阳， 刘义， 赵鸿铁， 等. 型钢混凝土异形柱框架节点承载力试验研究[J]. 土木工程学报， 2011， 44（5）：41-48.

Xue Jianyang， Liu Yi， Zhao Hongtie， et al. Experimental study of the bearing capacity of steel reinforced concrete special-shaped column-beam joint [J]. China Civil Engineering Journal， 2011， 44（5）： 41-48.

[5] 陈宗平， 徐金俊， 薛建阳. 型钢混凝土异形柱-钢梁空间边节点的抗震性能及影响因素分析[J]. 工程力学， 2015， 32（2）： 105-113.

Chen Zongping， Xu Jinjun， Xue Jianyang. Seismic and influence factor analysis on 3D side joints composed of steel reinforced concrete special-shaped columns and steel beams [J]. Engineering Mechanics， 2015， 32（2）： 105-113.

[6] 薛建阳， 刘祖强， 葛鸿鹏， 等. 实腹式型钢混凝土异形柱中框架抗震性能试验研究[J]. 建筑结构学报， 2011， 32（11）： 82-88.

Xue Jianyang， Liu Zuqiang， Ge Hongpeng， et al. Seismic behavior of solid steel reinforced concrete middle frame with special-shaped columns[J]. Journal of Building Structures， 2011， 32（11）： 82-88.

[7] 薛建阳， 刘祖强， 赵鸿铁， 等. 实腹式型钢混凝土异形柱边框架抗震性能试验研究[J]. 土木工程学报， 2012， 45（9）： 55-62.

Xue Jianyang， Liu Zuqiang， Zhao Hongtie， et al. Experimental study on seismic behaviors of solid steel reinforced concrete edge frame with special-shaped columns[J]. China Civil Engineering Journal， 2012， 45（9）： 55-62.

[8] Priestley M J N， Kowalsky M J. Aspects of drift and ductility capacity of rectangular cantilever structure walls[J]. Bulletin of the New Zealand National Society for Earthquake Engineering， 1998， 31（2）：73-85.

[9] 胡宗波. SRC异形柱空间框架结构振动台试验及平扭振动反应分析[D]. 西安： 西安建筑科技大学， 2018.

Hu Zongbo. Research on shaking table test and lateral-torsional vibration response of SRC spatial frame structure with special-shaped columns[D]. Xi'an： Xi'an University of Architecture & Technology， 2018.

[10] Clough R W， Penzien J. Dynamics of Structures[M]. New York： McGraw-Hill， 1993：511-523.

[11] Labat D. Recent advances in wavelet analyses： Part 1： A review of concepts[J]. Journal of Hydrology， 2005， 314（1）：275-288.

[12] Spacone E， Fillppou F C， Taucer F F. Fiber beam-column model for non-linear analysis of R/C frames： Part l. Formulation[J]. Earthquake Energy and Structure Dynamics， 1996， 25（7）：711-725.

[13] 叶燎原， 潘文. 结构静力弹塑性分析（Push-over）的原理和计算实例[J]. 建筑结构学报， 2000， 21（1）： 37-51.

Ye Liaoyuan， Pan Wen. The principle of nonlinear static analysis （Push-over） and numerical examples[J]. Journal of Building Structures， 2000， 21（1）： 37-51.

[14] FEMA. NEHRP guidelines for the seismic rehabilitation of buildings[R]. FEMA-273， Washington D. C.，1997.

作者簡介： 胡宗波（1985-），男，工学博士，副教授，博士后研究人员。电话：15398033685;E-mail：huzongbo_1985@163.com