碳纤维复合杆柱井下动力学仿真分析

孙秀荣

（河北环境工程学院，河北 秦皇岛 066102）

0 引言

碳纤维连续抽油杆具有质轻、高强、耐腐蚀等优越特性，在国内一些油田逐步得到了规模化应用[1-3]。与钢制杆抽油杆柱不同，碳纤维连续抽油杆一般由上部碳纤维杆和下部加重钢制杆组成。碳纤维杆以碳纤维材料为内心，壳层为玻璃纤维材料，两者结合处是玻璃纤维缠绕层[4-5]。作为一种新型材料，其力学性能备受关注。文献［6-7］对碳纤维抽油杆柱进行了超冲程分析；文献［8-9］对碳纤维抽油杆柱展开纵向振动力学分析，求出了固有频率等参数。上述研究均未考虑杆柱的横向变形，而碳纤维杆柱在井下运动过程中，是被局限在油管的狭小空间内，杆柱的在油管径向尺寸上的变形，直接决定了碳纤维杆柱是否有偏磨、断杆和脱扣现象，以及杆柱寿命情况是否受影响。本文立足于碳纤维杆柱在油管内的径向动力学变形，研究碳纤维杆柱断杆、脱扣机理。

1 力学模型

不考虑碳纤维杆柱的扭转变形，假设油管完全竖直状态，碳纤维复合杆柱轴心与油管中心重合。以碳纤维杆柱的井口为坐标原点，杆柱在油液中除了受底端的往复性端部载荷P(t)以外，还受到油管不同深度位置处分布节点载荷q(x)。在上述假设条件下，建立图1所示的复合杆柱横向弯曲变形的力学模型。

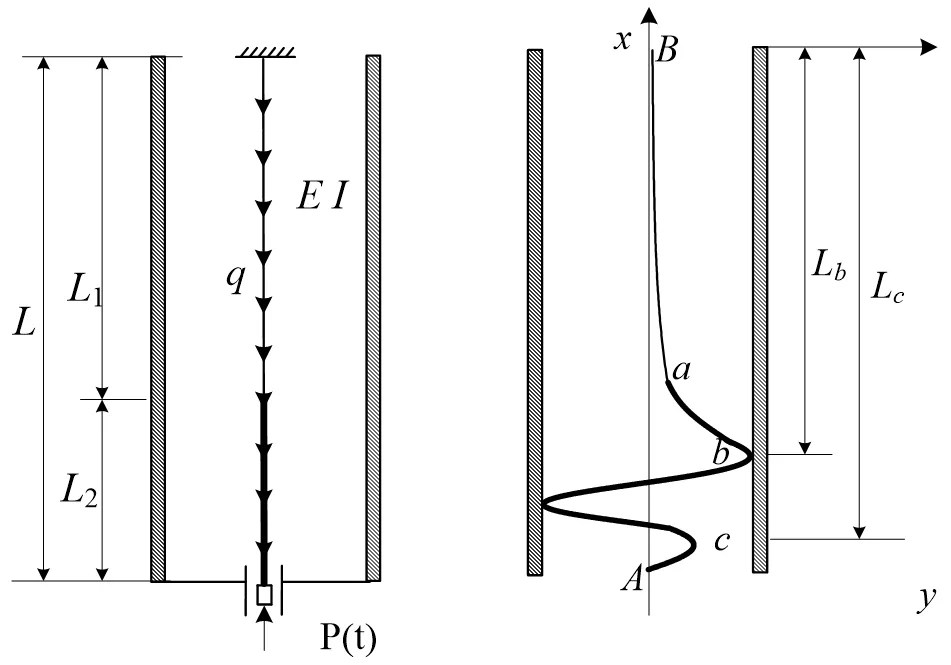
图1 杆柱受力和横向弯曲变形

2 数学模型

将整根碳纤维连续杆柱的弯曲变形分为三部分：上部段、中间段（杆管接触）、下部段，两段连接处满足连续性条件，即位移相等、转角相等、弯矩相等。在实际抽油过程的下行程某一时间段，按照杆柱受力分析可知，碳纤维材料杆柱为柔性杆柱，只受拉力，不受压力。而钢制杆柱可以处于受拉或受压状态，其某一位置点（中位点）至底端杆柱超过受压极限载荷出现屈曲变形，中位点以上则处于受拉状态。按工程实际，杆柱由于屈曲导致的接触段全集中在钢制杆，钢制杆柱屈曲变形段则与油管内壁接触[10]。因此，上述变形阶段中，中间段和下部段均假设为钢制杆，上部段则由碳纤维材料杆和钢制杆合并组成。

中间段杆柱屈曲假设完全与油管内壁接触，即变形为圆柱螺旋形状，其变形微分方程为：

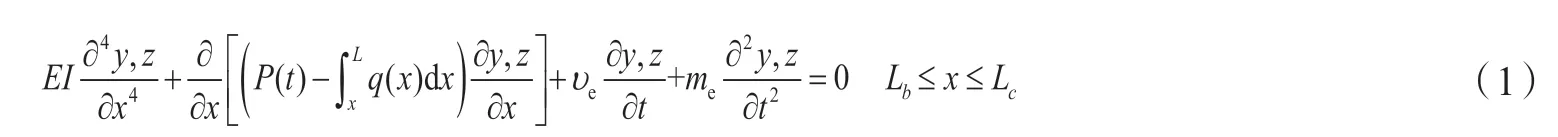
上部段包含两部分：上面的部分为碳纤维材料，下面的部分为钢质材料，两部分均不与油管内壁接触，其变形微分方程为：

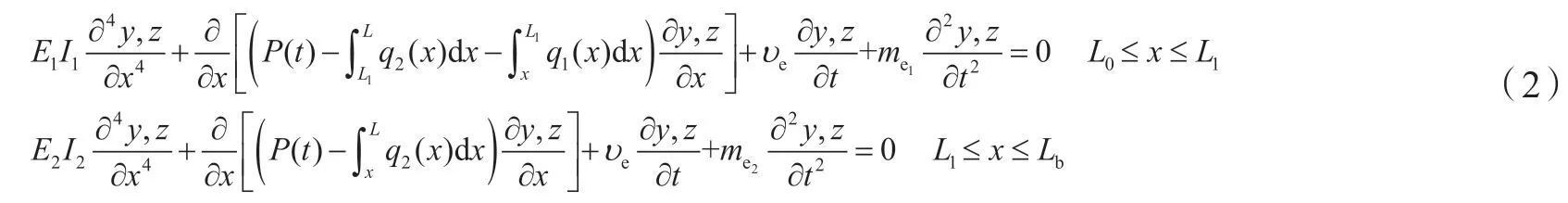
碳纤维材料杆和钢制材料杆交界处连续性条件：

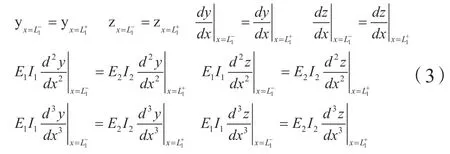
底部段变形微分方程为：

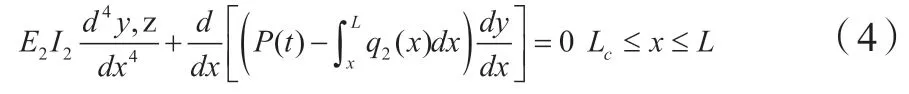
碳纤维杆柱顶端的边界假设为固定端，钢制杆的底部假设为可滑动的固定端，则边界条件为：

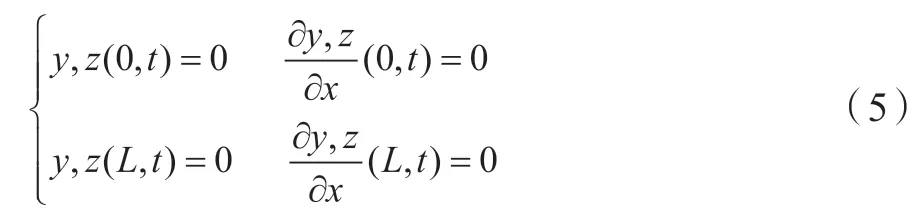
假设碳纤维复合杆柱的初始条件为竖直状态，即：

碳纤维复合杆柱在油井中往复运动，底部抽油泵柱塞位置处杆柱的载荷也是随往复运动而变化的，其变化曲线如图2所示：

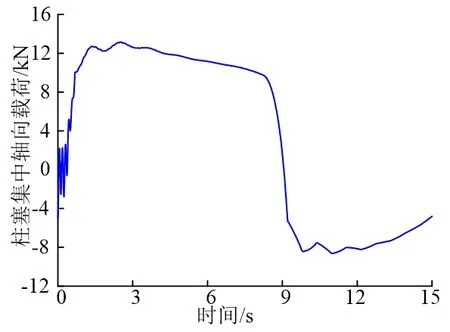
图2 端部柱塞载荷变化规律

由于杆柱的中下部段出现了屈曲变形，此变形作为横向动力学的空间位移激励，相应时刻杆柱的屈曲变形为：

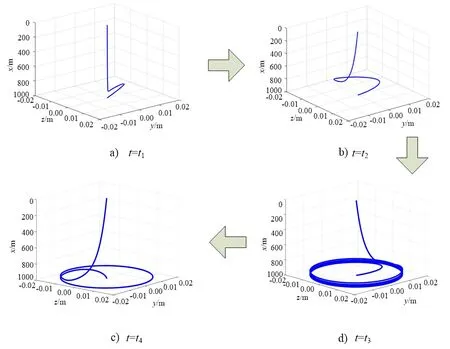
3 数值仿真方法

此方程为变系数高阶线性微分方程，含耦合变量时间变量t和空间变量x。当杆柱产生的弯曲变形与油管内壁接触后，将与油管壁面产生碰撞后反弹，碰撞过程的发生为非线性接触问题。因此分析整个过程需要分为两部分：求解高阶变系数线性耦合微分方程和接触碰撞问题的简化处理。

接触碰撞问题本文引入较常用的方法恢复系数法，即当杆柱节点与油管壁发生碰撞后，节点沿圆周径向的速度发生反向，节点切向的速度方向和大小不变，且碰撞后节点落在油管内壁上，参见文献[11-12]。

高阶变系数线性耦合微分方程无法采用解析方法求解，最理想的方式为数值分析方法。本文采取有限差分法和Newmark-β法相结合的方法，有限差分法用于离散空间变量x，Newmark-β法用于离散时间变量t。空间离散的模型如图3所示，将整个细长杆柱离散成n个单元，n+1个节点，以碳纤维杆和钢制杆连接处为分界点，分别采用不同的步长∆x1和∆x2，时间步长均为∆t。

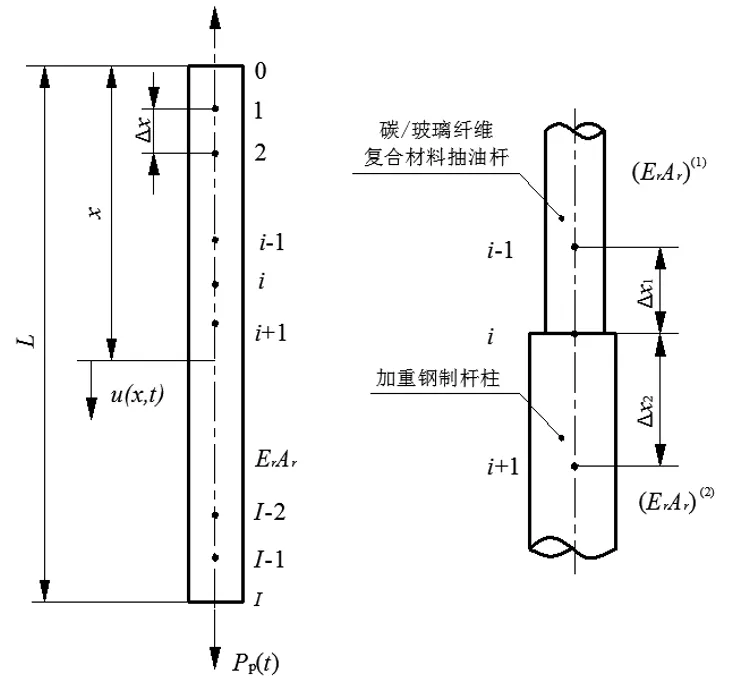
图3 空间节点离散

则空间离散并进行中心有限差分后，两边界处的差分形式为：

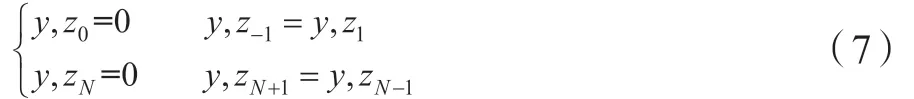
同理，将杆柱边界范围内的空间节点进行差分处理，得到不同节点处各阶差分形式(8-10)：

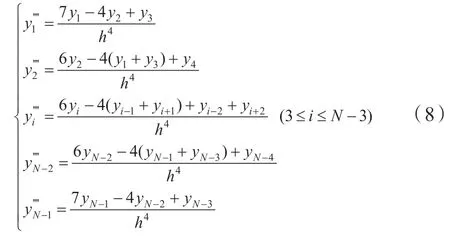
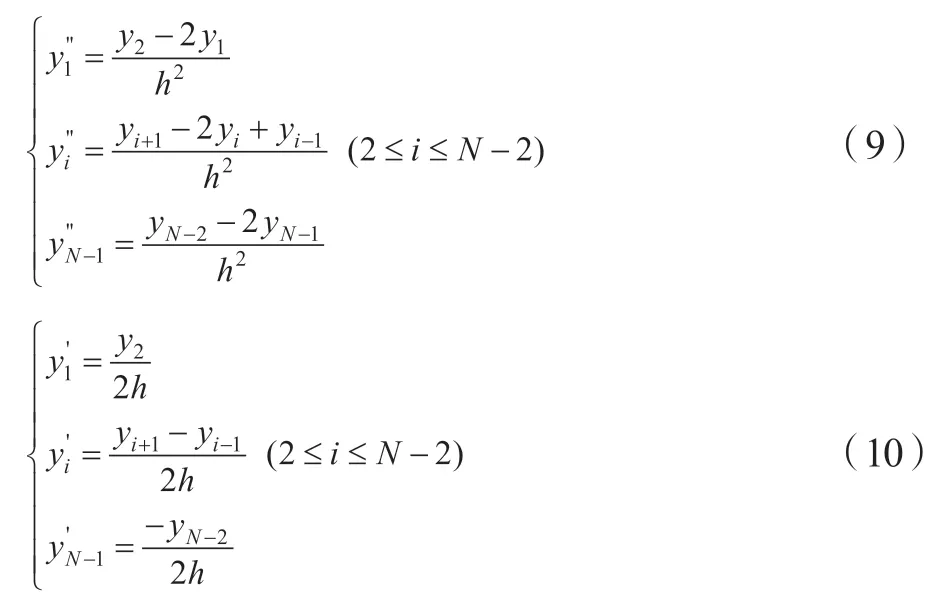
采用Newmark-b法对时间进行离散，按Newmark-b假设形式，则有：

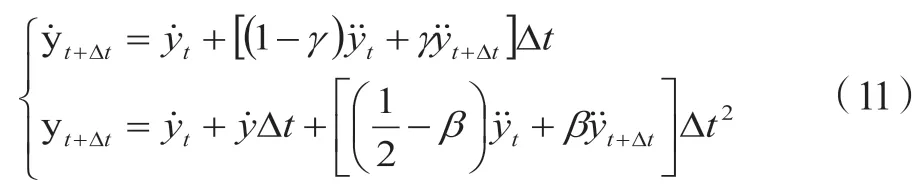
式中，β和γ是积分精度相关的参数。当β≥0.5，γ≥0.25（0.5+β）2时，为无条件稳定的形式。本文取β=0.5，γ=0.25，满足稳定条件。由式（11）得到的表达式，即：

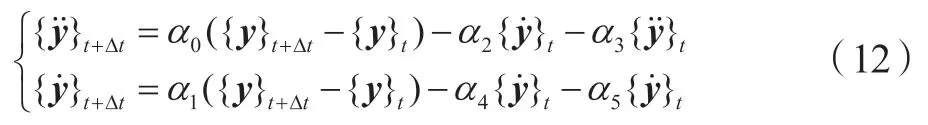
则进一步得到t+∆t时刻的微分方程：

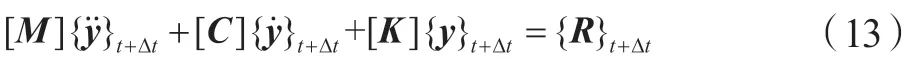
将式（12-13）代入（14），得到关于yt+∆t的方程

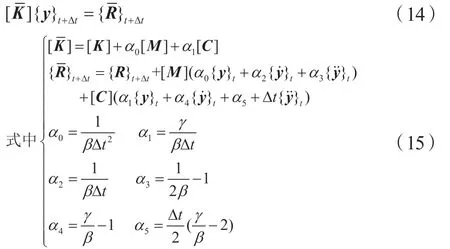
4 仿真结果

4.1 基本参数

碳纤维杆柱组合形式为二级杆柱：一级杆为19mm×1700m的碳纤维杆柱，二级杆为25mm×500m的钢杆。钢质杆弹性模量E2=206 GPa，碳纤维杆弹性模量E1=103 Gpa。分布轴向力为如图4所示，分布轴向力随杆柱的节点位置和运动瞬时时刻而变化。其他相应参数如图5所示。

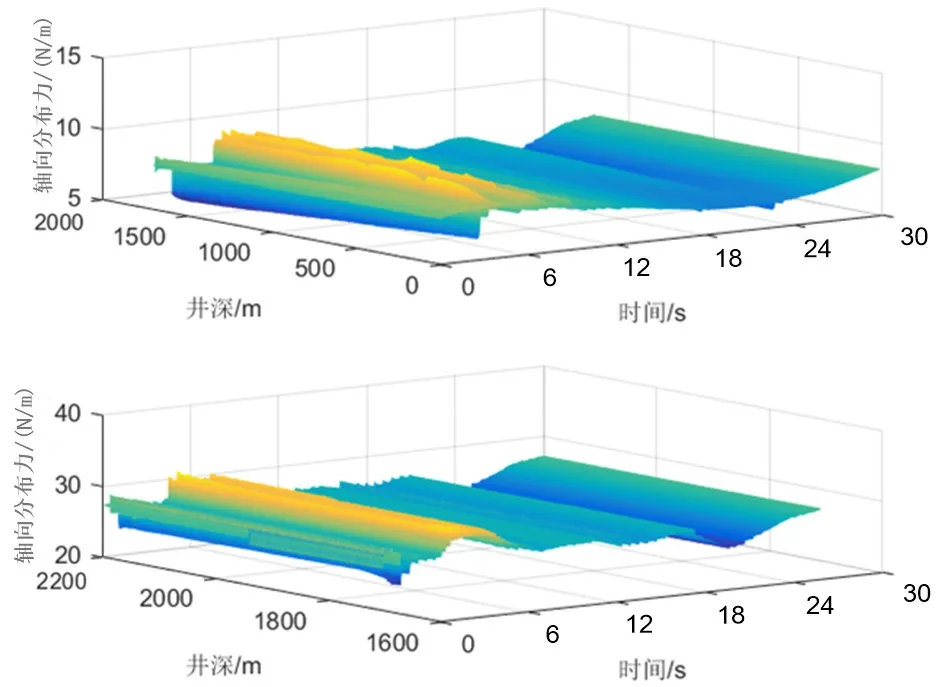
图4 碳纤维复合杆柱不同节点位置处的分布载荷

4.2 杆管接触的仿真结果

经数值仿真得到了碳纤维复合杆柱随井深和抽油时间变化的规律，如图5所示。由图可知，碰撞接触力在中下部相比上部段碰撞接触力显著增长，具有较大碰撞力的杆柱位置分布在钢制杆上，而中上部碳纤维杆柱碰撞力很小。由此说明，碳纤维材料的杆柱能有效减少杆管的接触碰撞，即相应的延长杆柱的寿命。

仿真界面的基本参数

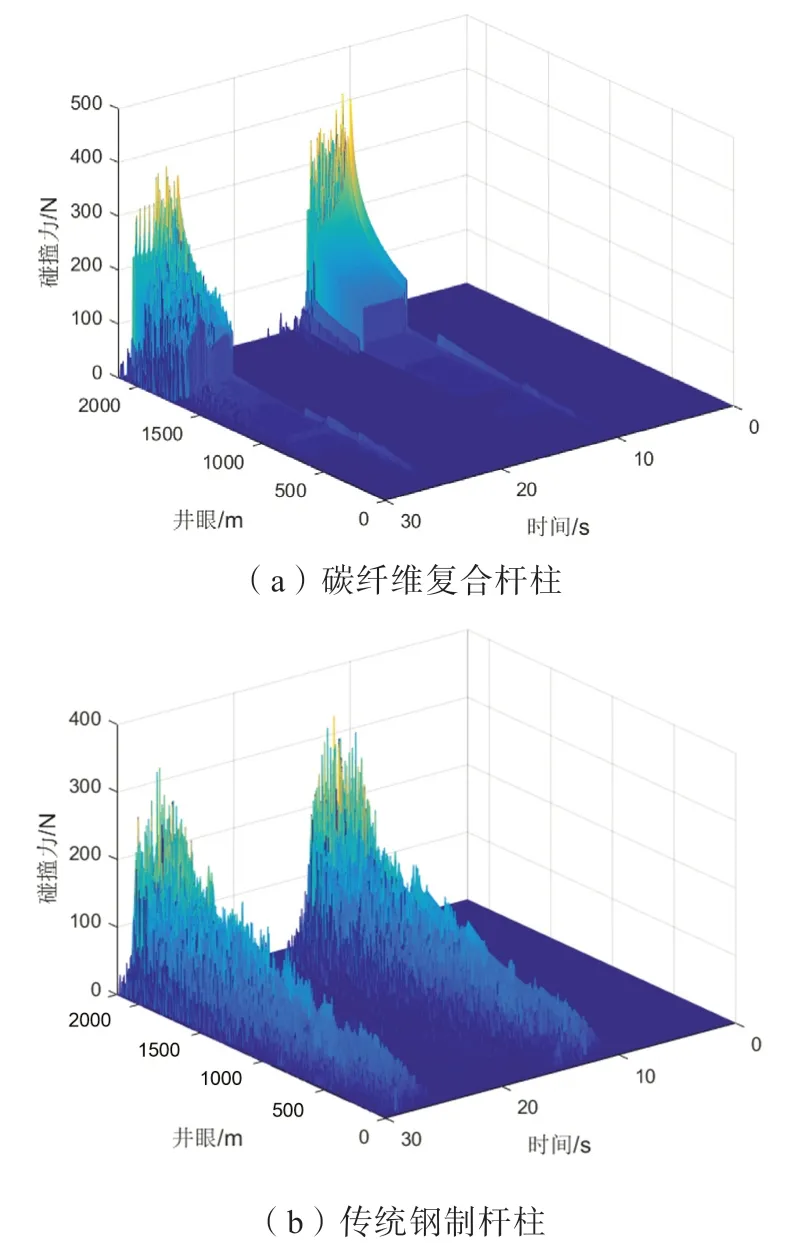
图5 接触力变化

4.3 杆柱弯曲应力

对数值仿真结果进一步进行处理，得到了杆柱在油管内产生动力学弯曲变形后的弯曲应力分布，如图6所示。图6a为钢制杆部分弯曲应力分布，图6b为碳纤维杆柱弯曲应力分布。由图可知，在一个行程内，碳纤维杆和钢制杆的弯曲应力最大值随着井深的增加而增大，碳纤维杆的最大弯曲应力可达30MPa，钢制杆的最大弯曲应力可达150MPa。钢制杆的弯曲应力并为超过本身的屈服极限，说明钢制杆在井眼内的受力多为往复磨损及疲劳破坏。而碳纤维杆受到的弯曲应力大幅减小，碳纤维杆柱的寿命大大延长。

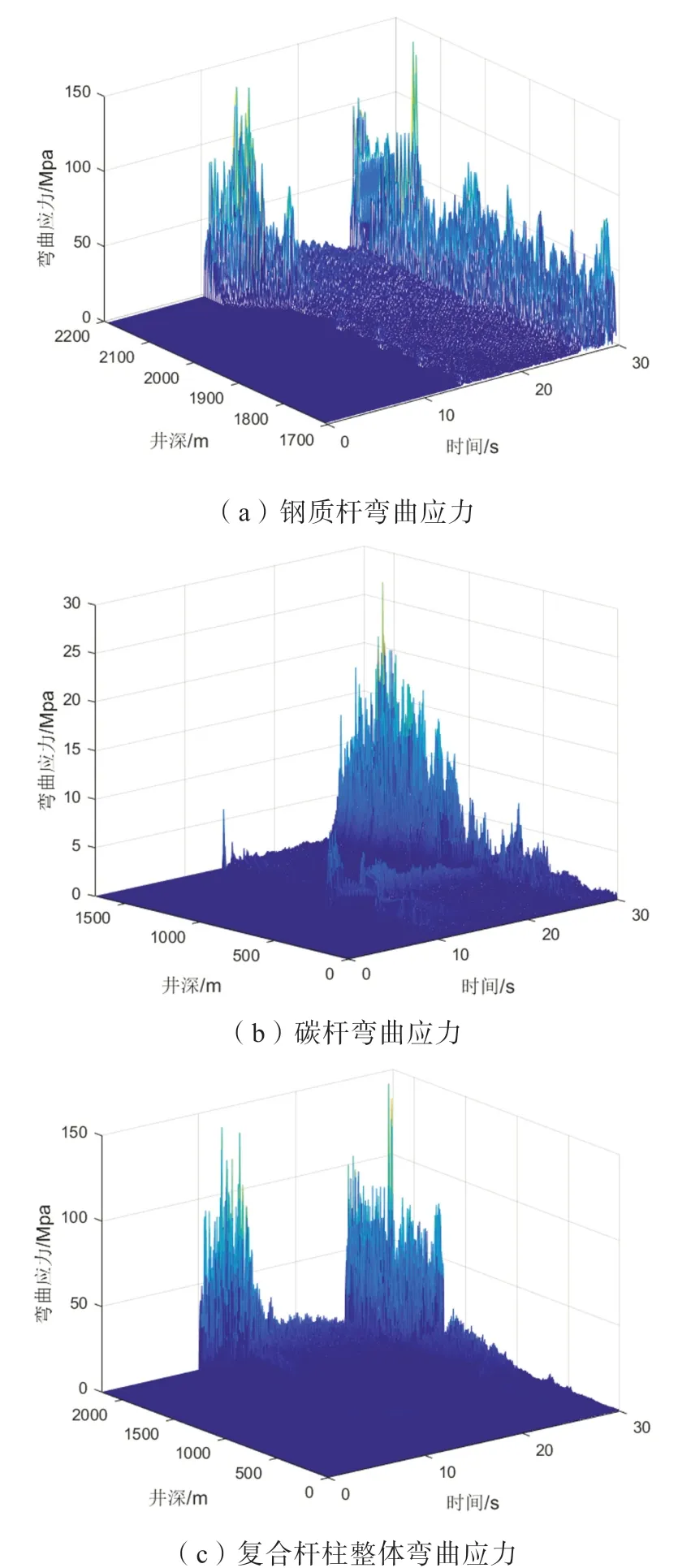
图6 碳纤维复合杆柱弯曲应力变化

5 结论

本文建立了碳纤维复合杆柱的横向动力学仿真模型，对杆柱和油管的横向碰撞和接触力进行了仿真分析，得到如下结论：

（1）碳纤维-钢制杆复合杆柱与油管发生碰撞剧烈的位置在钢制杆靠近底端几十米至几百米之间，上部碳纤维杆的碰撞明显较弱，且碰撞力较低，说明碳纤维复合杆柱主要在钢制杆处发生偏磨，而传统钢制杆柱偏磨几乎发生在全井。因而，碳纤维杆柱的杆管偏磨现象大大降低。

（2）杆柱在油管内发生弯曲变形的应力并未超过材料许用应力，材料仍在弹性范围内变形。说明发生的破坏多是疲劳磨损。

（3）本文的动力学仿真结果验证了碳纤维杆的良好的力学性能和较低的杆管接触偏磨现象，解释了碳纤维杆相比全钢制杆具有较长寿命的原因，为碳纤维杆的工程应用提供了理论支撑。