叠箱式模块化建筑内力计算方法研究
赫连光泽,周学军,王振
(山东建筑大学 土木工程学院,山东 济南 250101)
0 引言
模块化建筑是一种集成化程度较高的装配式建筑,已经成为新型建筑技术的主要发展方向之一[1]。叠箱式模块化建筑是由若干个模块单元堆叠而成的装配式建筑,每个模块单元均在工厂进行内部墙板、屋面板、管线、管道安装,完成安装后运输至施工现场,通过角件等节点连接构造进行连接装配,主要受力体系为柱承重的钢框架体系。由于模块单元之间多采用角件连接,其连接为半刚性连接[2],同时节点区域存在多梁多柱并存的问题。因此,普通框架计算模型简化分析方法不能直接运用到叠箱式模块化建筑的结构性能分析。
许多学者提出半刚性连接框架的有限元分析方法,通过分析节点柔性连接以及构件几何非线性特性研究了半刚接的框架内力,但计算以及模型建立较为复杂。查晓雄等[3]通过有限元分析软件ABAQUS对六层集装箱模型进行数值模拟,推导了摩擦系数和阻尼比之间的关系,得到了各层的等效阻尼比。左洋等[4]基于蒙皮理论分析箱体侧壁波纹板的刚度问题,进而推导出单个集装箱的刚度,并且利用有限元软件验证了公式的正确性。CAO等[5]利用有限元软件分析多层集装箱结构在水平荷载作用下的稳定性、位移变形能力以及内部构件的应力,对集装箱结构提出利用加强带固定的设计建议。
文章通过结构力学方法,以多层箱式模块化建筑为例,在已知半刚性节点的初始转动刚度前提下,分析了叠箱式模块化建筑的简化计算模型,推导其在竖向荷载和水平荷载作用下的简化计算公式,并对比验证了简化计算模型与数值模拟结果。
1 叠箱式模块化建筑竖向荷载作用下简化计算方法
1.1 弯矩分配法在叠箱式模块化建筑上的应用
目前,随着有限元方法的迅速发展,对结构进行计算方法简化研究具有重要意义,设计人员可以根据简化计算结果对有限元模型的合理性进行验证,并选择合理的结构设计方案[6]。叠箱式模块化建筑受到竖向荷载作用时的变形如图1所示。
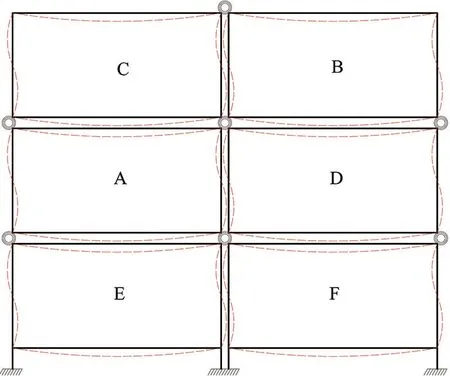
图1 叠箱式模块化建筑竖向荷载下变形图
由于模块单元之间半刚性节点的存在,相邻模块单元因发生变形而产生弯矩,普通框架弯矩分配法中将单个杆件视为基本构件的假定不再适用于叠箱式模块化建筑。参考弯矩分配法计算框架结构在竖向荷载作用下内力的思路,采用平衡条件剖析法[7],计算模块单元内力时,对其余模块单元内部梁柱节点附加刚臂约束,将叠箱式模块化建筑每个模块单元视为基本构件,分配弯矩,再将半刚性连接节点处的弯矩在模块单元内部进行分配。
1.1.1 模块单元固端弯矩
模块单元竖向集中荷载作用下的计算简图如图2所示,以集中荷载作用下的单个模块单元为例,通过位移法可求解模块单元A的固端弯矩[8]。由位移法计算模块单元固端弯矩,其计算过程由式(1)~(4)表示为

图2 模块单元竖向集中荷载作用下计算简图
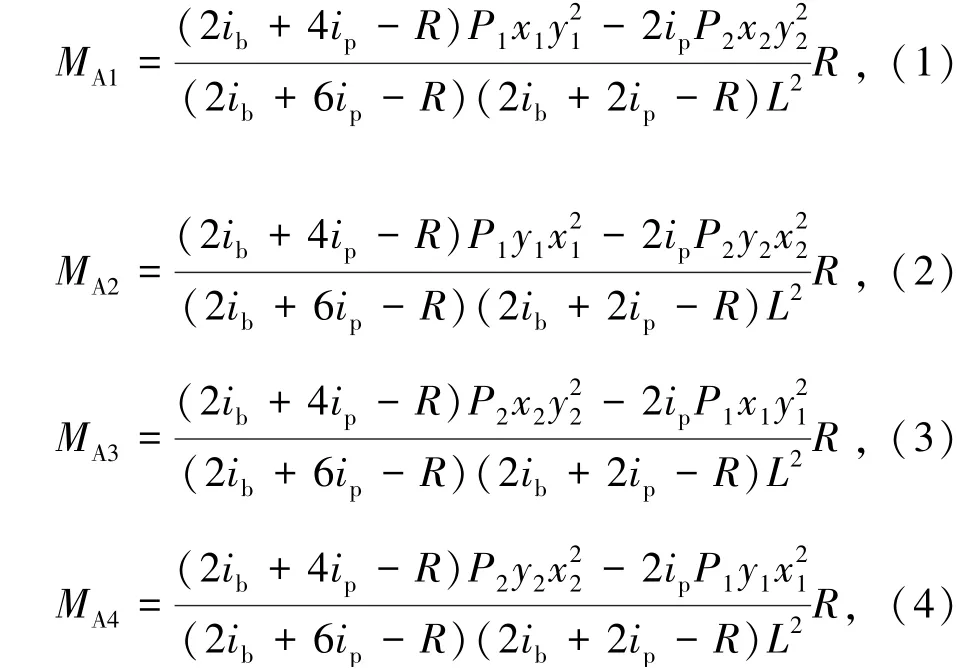
式中MA1、MA2、MA3、MA4分别为模块单元节点A1、A2、A3、A4的固端弯矩,kN·m;P1、P2分别为作用在梁A1A2和梁A3A4的集中力,kN;R为半刚性节点的转动刚度,(kN·m)/mrad;ib为模块单元梁的线刚度,kN·m;ip为模块单元柱的线刚度,kN·m。
简化式(1)~(4)的计算结果,最终得到模块单元固端弯矩的表达式,由式(5)~(8)表示为


式(5)~(8)同样适用于均布荷载及其他荷载作用下模块单元固端弯矩的计算,只需将M P1、M′P1、M P2、M′P2换成相应荷载作用在两端刚接梁的固端弯矩。
1.1.2 模块单元的转动刚度
计算模块单元转动刚度时,考虑了半刚性连接节点的影响,在模块单元梁柱接触处施加附加刚臂约束。模块单元梁柱线刚度如图3所示,R为半刚性节点初始转动刚度;与半刚性连接框架相同,θAM(M=1,2,3,4)为AM处假设节点为铰接时节点转角;θrAM(M=1,2,3,4)为半刚性节点的节点转角。
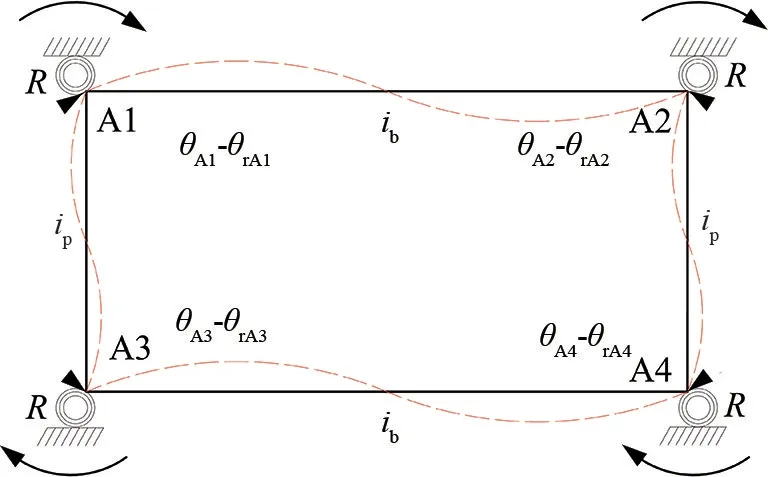
图3 模块单元添加刚臂约束计算简图
以A1节点为例,梁A1A2、柱A1A3的转角位移方程由式(13)~(14)表示为
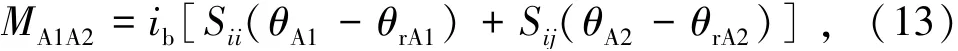

由于模块单元梁的轴力很小,可以忽略不计,所以稳定函数取值为S ii=4、S ij=2。
同理,可以得到模块单元其他构件转角位移方程。由A1、A2、A3、A4等4个节点弯矩平衡,得到4个节点弯矩平衡方程,由式(17)~(20)表示为
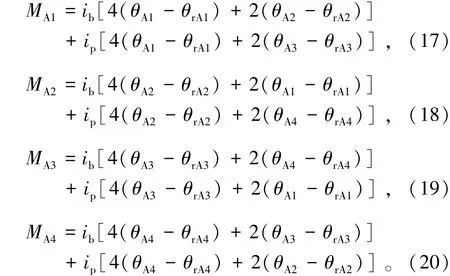
联立(17)~(20),根据转动刚度的定义,转动刚度矩阵由式(21)[10]表示为
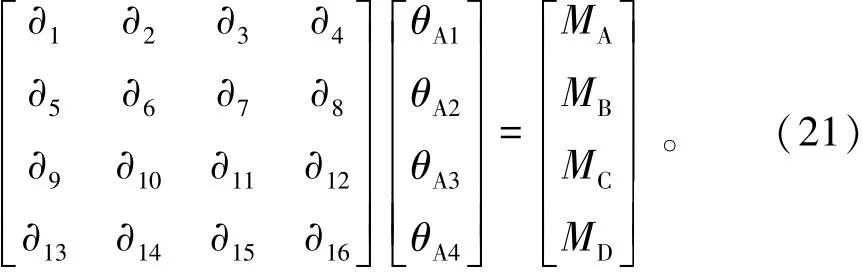
模块单元在A1、A2、A3、A4点的转动刚度分别为SA1=∂1、SA2=∂5、SA3=∂9、SA4=∂13,其中∂M(M=1,5,9,13)有且仅有梁柱线刚度和半刚性节点转动刚度组成。
1.1.3 分配系数
叠箱式模块化建筑结构计算简图如图4所示,以模块单元A、B、C、D公共节点处为例,模块单元A在A2处分配系数μ可由式(22)[10]表示为
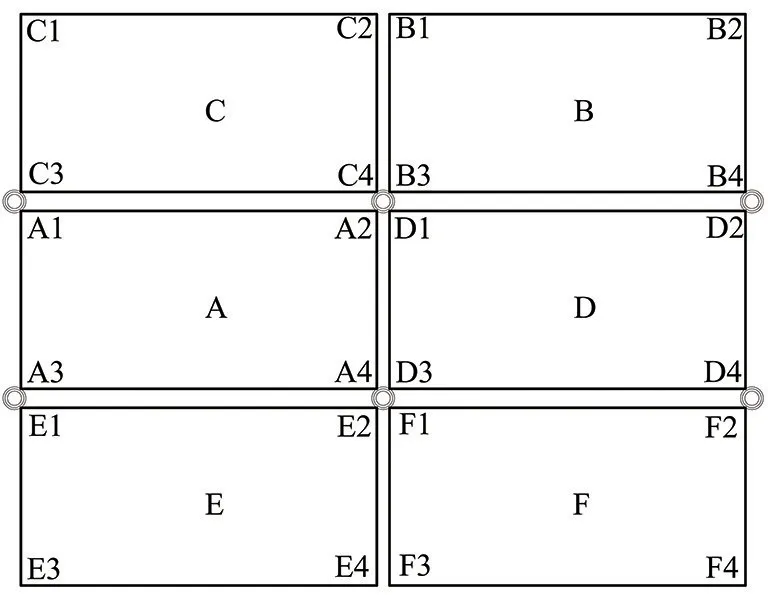
图4 叠箱式模块化建筑结构计算简图

1.1.4 传递系数
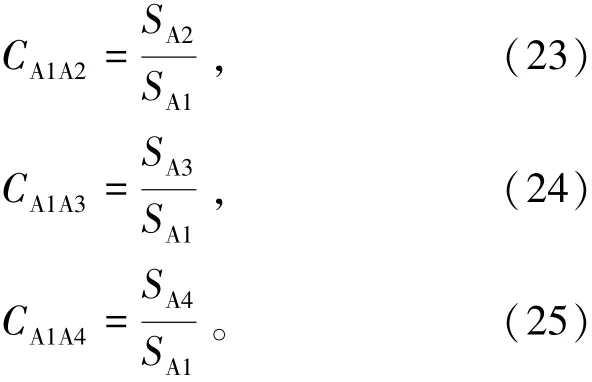
以图2中模块单元A为例,节点A1的弯矩会向A2、A3、A4传递。传递系数可由式(23)~(25)[10]表示为
1.2 基于分层法的计算模型简化
对分析叠箱式模块化建筑采用的分层法做如下假定:(1)在竖向荷载的作用下,叠箱式模块化建筑的侧移可以忽略不计,用弯矩分配法计算;(2)每层模块单元梁上的竖向荷载对其他层的模块单元梁及非相邻模单元柱的内力影响忽略不计,把多层模块化建筑分成一层一层单独计算。采用分层法计算每层叠箱式模块内力时,可只考虑该层叠箱式模块,在同层模块之间进行力矩分配即可。由上述假定,多层叠箱式模块化结构在竖向荷载作用下可分层计算。
1.3 算例1
采用弯矩分配法求解模块单元内力,由于模块单元层之间节点处的连接方式一致,模块建筑整体进行了规则化设计,模块单元之间的传力方式相同,内力值的大小仅由固端弯矩、转动刚度、弯矩分配系数、弯矩传递系数决定。对双层模块单元的内力传递方式及简化计算方法进行研究,计算简图如图5所示,模块单元梁、柱几何性质为Ib=2.31×10-4m4、Ic=4.77×10-5m4、转动刚度R=39.60(kN·m)/mrad。
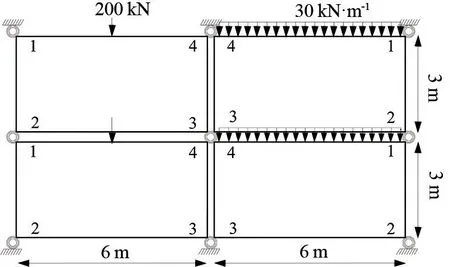
图5 双层模块单元计算简图
根据《欧洲规范3:钢结构设计 第1.1部分:一般规则和建筑物规则》(Eurocode 3:Design of steel structures-Part 1.1: General rules and rules for buildings,EC3:1.1)[11],半刚性节点在弹性阶段内的连接刚度进行二分之一折减,则计算时所采用的连接刚度Rk=R/2=19.8(kN·m)/mrad。通过式(5)~(8)计算一层模型固端弯矩,根据转动刚度的刚度矩阵即式(21)计算转动刚度,进而得到弯矩分配系数和弯矩传递系数,整理计算模型弯矩计算系数见表1,表中WL和WR分别代表左侧节点和右侧节点。根据分层法的假定,把多层模块化建筑分成独立层单独计算,基于结构力学基本理论计算独立层梁柱弯矩,然后叠加两层柱端弯矩,最终弯矩分布如图6所示。

表1 弯矩计算系数表
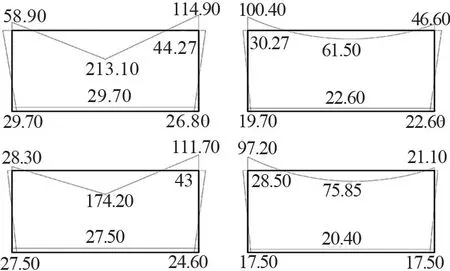
图6 内力简化计算结果图/(kN·m)
利用通用结构分析与设计软件Midas Gen建立有限元分析模型,对算例中的模块单元进行数值模拟计算[12]。在有限元模型中,叠箱式模块化建筑的梁与柱均采用一般梁单元进行模拟。该单元使用一般的三维梁-柱公式,能够考虑包括双轴弯曲、扭转、轴向变形、双轴剪切变形等效应;模块单元之间采用弹簧单元模拟连接节点,该弹簧能够约束相邻模块单元的平动位移并具有相应的转动刚度和转动能力。模块单元的弯矩内力数值模拟结果如图7所示。
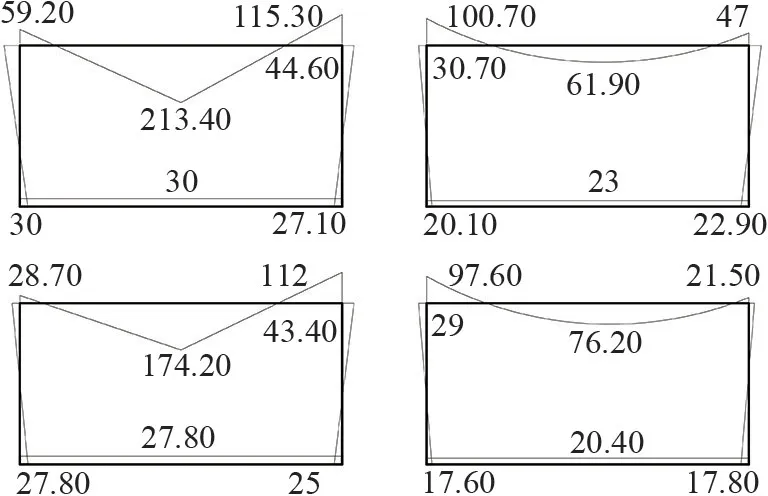
图7 基于Midas Gen的数值模拟结果图/(kN·m)
通过对比弯矩内力简化计算结果(如图6所示)和数值模拟结果(如图7所示)可发现,构件的弯矩内力简化计算结果和数值模拟结果较吻合,误差很小,说明采用简化计算方法与有限元数值模拟方法对模块单元进行弯矩内力计算的结果一致性较高,简化计算方式较合理。
2 叠箱式模块化建筑水平荷载作用下简化计算方法
2.1 D值法在叠箱式模块化建筑上的应用
计算结构的位移时需要计算结构抗侧刚度[13],叠箱式模块化建筑柱子的抗侧刚度及反弯点位置与模块单元柱两端转角有关[14]。对比普通框架D值法推导叠箱式模块化建筑柱抗侧刚度D,做以下假定:(1)水平荷载作用下模块内单元梁柱节点与相临的模块单元节点转角相同。(2)水平荷载作用下上下模块单元柱的弦转角及线刚度相同。根据以上两个假定,可以将模块单元之间的半刚性连接节点简化为铰接节点如图8所示。通过对D值和反弯点的修正,可求出叠箱式模块化建筑在水平荷载作用下的层间位移和内力。
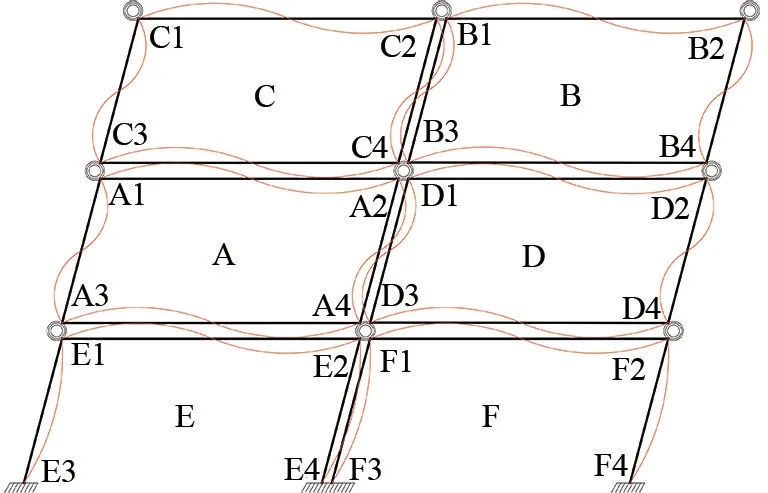
图8 叠箱式模块化建筑水平荷载作用下变形图
2.1.1 一般层模块单元柱抗侧刚度修正
以一般层模块单元A为例,如图9所示,其梁柱转角位移方程由式(26)和(27)[10]表示为
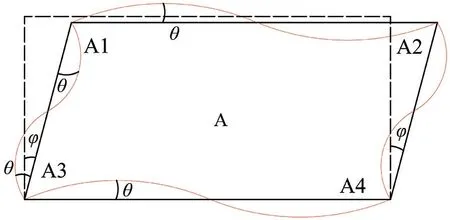
图9 一般层模块单元水平荷载作用下变形图
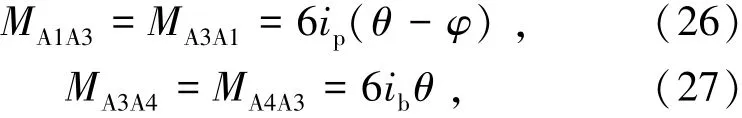
式中θ为节点转角;φ为柱弦转角,φ由式(28)表示为

式中Δ为柱侧移,m;h为柱高度,m。
若使节点A1、A3力矩平衡,则应满足的条件由式(29)和(30)表示为
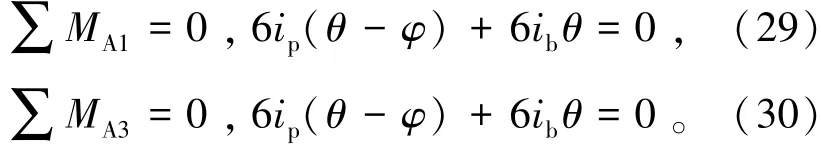
由此推导模块单元梁柱线刚度比,由式(31)和(32)表示为
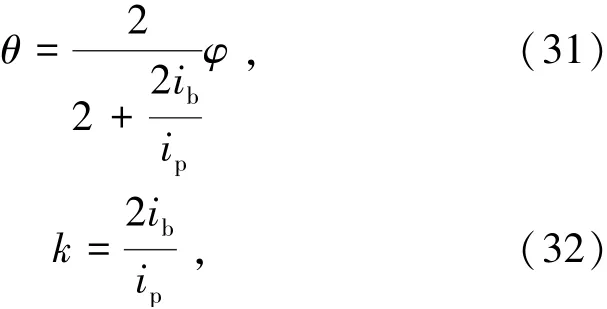
式中k为梁柱线刚度比。
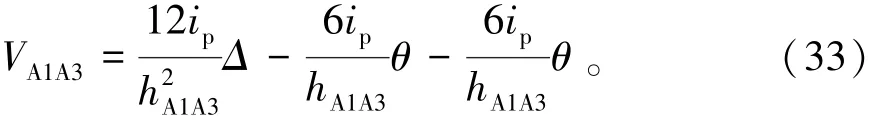
联立(28)~(33)得

式中α为抗侧刚度修正系数,
当Δ=1时,就是考虑两端有转角的侧移刚度DA1A3,由式(35)表示为
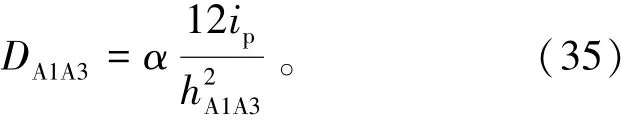
2.1.2 底层模块单元柱抗侧刚度修正
以底层模块单元E为例,如图10所示,其梁柱转角位移方程由式(36)和(37)表示为[10]
图10 底层模块单元水平荷载作用下变形图
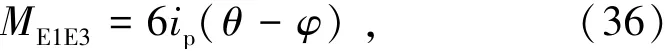

若使节点E1力矩平衡,由式(38)表示为
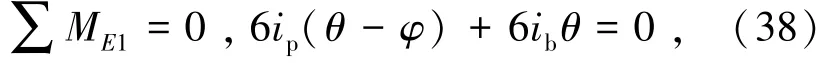
则
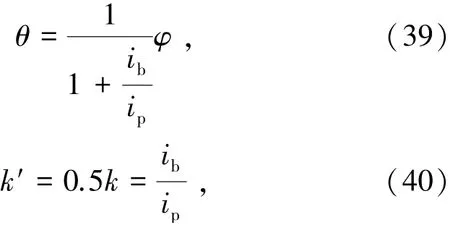
式中k′为底层梁柱线刚度比。
模块单元柱剪力VE1E3由式(41)表示为
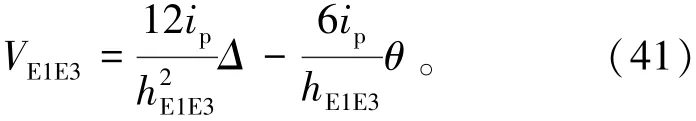
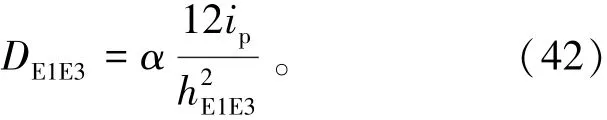
2.1.3 叠箱式模块化建筑的反弯点高度
一般框架结构梁的线刚度和层高会有所变化,影响其柱反弯点高度[15]。对于叠箱式模块化建筑,模块单元在工厂中加工预制工业化程度极高[16]。在同一建筑中模块单元的横梁线刚度不变,层高保持固定的模数,所以为了方便简化模块化结构的计算,可认为叠箱式模块化建筑中上、下模块单元柱端转角相同,即反弯点位于模块单元柱的中点。
2.1.4 叠箱式模块化建筑侧移计算
水平荷载作用下的普通框架结构变形包括总体剪切变形和总体弯曲变形[17]。对于叠箱式模块化建筑,除以上两种变形外,还包括模块单元节点连接处的水平滑动变形。由于节点连接处的角件和连接板均为工厂预制,现场进行可靠连接安装时,具有较大的抗剪刚度,故节点连接处的水平滑动变形可以忽略。因此,叠箱式模块化建筑的侧移计算与普通框架一致,只需用式(35)~(43)替换普通框架的D值即可。
2.2 算例2
根据D值法对3层两跨叠箱式模块化建筑的侧向位移进行分析计算,计算简图如图11所示,模块单元的梁、柱相关的几何性质有:Ib=2.31×10-4m4、Ic=4.77×10-5m4、转动刚度R=39.60(kN·m)/mrad。
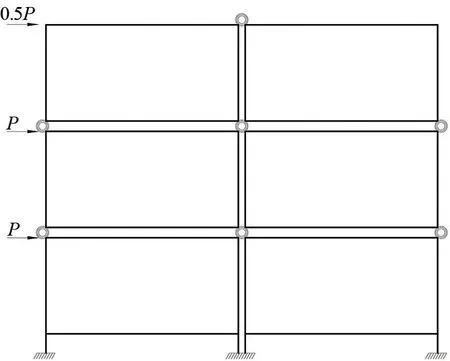
图11 计算简图
依据EC3:1.1[11]建议,半刚性节点在弹性阶段内的连接刚度进行二分之一折减,则计算时所采用的连接刚度Rk=R/2=19.8(kN·m)/mrad。按照2.1.1和2.1.2中给出的计算方法,整理模块单元柱的抗侧刚度修正系数:一般层的层边柱修正系数α1=0.3;一般层的层中柱修正系数α2=0.3;底层边柱修正系数α3=0.2;底层中柱修正系数α4=0.2。
整理D值法计算结果和数值模拟结果见表2,两者计算结果较为接近,说明文章提出的修正反弯点法能够精确地计算叠箱式模块化建筑结构在水平荷载下的侧移。理论计算结果小于数值模拟结果的原因则是由理论计算过程中忽略梁的轴向刚度造成的。

表2 水平荷载作用下位移表
3 结论
根据上述研究可以得出以下结论:
(1)提出了适用于叠箱式模块化建筑在竖向荷载下的计算模型及简化计算方法,该简化方法与有限元分析结果吻合度较高,可用于叠箱式模块化建筑初步设计与最终校核。
(2)建立了叠箱式模块化建筑的抗侧刚度计算方法,发现其公式形式与普通框架抗侧刚度计算公式较相似,修正了底层模块单元柱的抗侧刚度,确定了叠箱式模块化建筑模块单元柱的反弯点高度位于中点。
(3)计算叠箱式模块化建筑结构侧移时模块单元之间的半刚性连接节点可简化为铰接连接节点,简化计算方法与有限元数值分析结果吻合较好。

