适用于MMC-MVDC的无差拍最近电流逼近控制策略

郭汉臣，王 琛，王 毅,2，聂小鹏

(1.华北电力大学 河北省分布式储能与微网重点实验室，河北 保定 071003；2.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003)

0 引 言

目前在直流输电领域，对直流电网等级的划分国内外尚未形成统一标准。根据应用场景和我国电力行业发展情况，学者们将直流电网大致划分为三个等级：电压等级低于1.5 kV为低压直流电网，在1.5 kV和200 kV之间的为中压直流电网，高于200 kV为高压直流电网[1-3]。相比同等级的交流电网，中压直流(medium voltage direct current，MVDC)输电系统以其较低的输送成本和较少的损耗在海上风电系统、光伏发电系统和中压直流配电等领域有广阔的应用前景。模块化多电平换流器(modular multilevel converter，MMC)凭借高拓展性与低损耗等优势，在美国跨湾工程、舟山5端柔性直流输电工程等高压大容量工程中得以成功应用[4-7]，而中压直流系统中常用换流器为电压源换流器(Voltage Source Converter，VSC)。相比传统的VSC，MMC中直流母线电压在各子模块中均匀分配，从而对输出交流电压大小的调控更加方便，还可降低器件对耐压性的要求；同时分散电容使变换器对故障的应对能力更强，电平数量的增加使交流侧谐波含量降低[8-10]。因此，MMC在中压直流输电场合具有相当的应用价值。

目前MMC中的常用控制策略为最近电平逼近调制(nearest level modulation，NLM)以及载波移相脉冲宽度调制(carrier phase shifting pulse width modulation，CPS-PWM)。NLM以其原理和易于实现等优点，在高压直流输电(HVDC)系统中成为MMC的常用调制策略。而将MMC应用于MVDC系统时，子模块数量会随着电压等级的降低而变小，采用NLM时每一等效阶梯波内各电平的持续时间将变长，电平切换频率会降低，从而造成输出电流具有较大的畸变[11-13]。而采用CPS-PWM控制时，虽然电平跳变数的增加会使交流侧谐波畸变降低，但各子模块开关频率会大大增加，使MMC整体损耗升高，同时CPS-PWM在调制环节中需要对各子模块单独进行闭环电压控制，需对多组PI控制器进行参数整定，大大增加了控制系统的复杂度。而且由于IGBT自身允许的开关频率最大为2 000 Hz，故当子模块数量极少时，CPS-PWM对谐波特性的提升有限[14-16]。因此，如何降低少模块MMC输出波形谐波畸变，同时使系统中子模块开关频率尽可能保持在较低水平，是将MMC应用到中压直流输电系统面临的新问题。

为解决上述问题，学者们对现有控制策略的不足进行了研究，并在此基础上提出了多种改进型控制策略。文献[17-18]分别提出并改进了基于NLM和PWM的混合调制策略，该策略相比CPS-PWM子模块开关频率有所降低，交流侧电能质量相比NLM大大提高，但仍需要通过调制载波控制电平跳变次数，交流侧电能质量取决于载波频率的高低。文献[19，20]提出并将无差拍电流控制与NLM相结合，并将其用于中压直流背靠背系统。该方法对参考电流生成环节进行优化，与传统矢量控制相比，该控制方法不需要解耦控制，所需的PI调节器数量大大降低，但在用于MMC-HVDC系统时，仍需要对两侧的MMC单独进行PI参数调节，对调节参数要求较高。综上所述，为了兼顾电压电流的畸变率、控制系统的复杂程度和损耗，适用于MVDC输电系统中MMC的调制方法仍需进一步探索。

为解决上述问题，本文以无差拍控制和阶梯波调制为核心思想，提出了MMC的无差拍最近电流逼近(deadbeat nearest current modulation，DNCM)控制策略。该策略在每个电平持续时间内，通过参考电流和实际电流的差值计算电压变化量，从而控制电平的跳变次数，进而使各电平实际持续时间变短。该控制策略所需的PI调节次数极少，系统对控制参数的要求也大幅降低，计算速度也得以提升。本文首先阐述DNCM的调制和均压方法，再定量分析了DNCM控制策略通过电流误差控制电平切换的原理，最后在Matlab/Simulink中搭建了MMC-MVDC仿真模型，以验证本文所提控制策略的有效性。

1 MMC-MVDC的结构及原理

采用三相MMC的MVDC系统拓扑结构如图1所示，其中低压侧MMC作用为整流，高压侧MMC作用为逆变。图中Udc1代表整流侧MMC输出直流电压，Udc2代表逆变侧MMC直流输入电压，Idc为直流线路上的电流，ia2、ib2、ic2代表逆变侧MMC各相输出的电流，L2代表电网滤波电感，整流侧MMC同理。直流线路两侧MMC结构相同，各相分别含有2个桥臂，各桥臂均由一个桥臂电抗器L1与N个子模块(sub-module，SM)串联构成，各SM结构相同，均采用半桥子模块(HBSM)结构。子模块由2个IGBT分别为S1和S2和1个电容C组成。通过控制S1和S2的通断，即可使子模块输出电压Usm为电容电压或0，从而在每个桥臂上得到多种电平幅值。

图1 MMC-MVDC拓扑结构Fig.1 Topology of MMC-MVDC

由于两侧MMC结构相同，且MMC各相间存在对称性，因此可取高压侧MMC的A相单独分析，其他各相以此类推。对于图1，两侧MMC上A相两桥臂可视为并联关系，则忽略桥臂电感上产生的压降并对电感进行等效，可得等效后的电感Leq表达式如下式，等效后的逆变侧A相电路如图2所示。

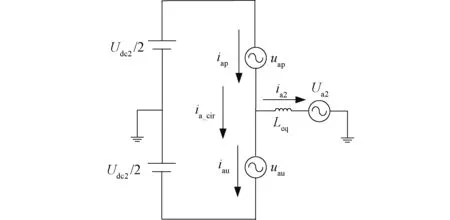
图2 逆变侧A相等效电路Fig.2 Equivalent circuit of phase A on inverter side

(1)

图中uap和uau分别表示A相上、下桥臂电压，iap和iau分别表示各桥臂电流，Ua2表示高压侧MMC的A相输出电压，ia_cir为A相的相内环流。由于桥臂电感对环流有抑制作用，故相内环流实际值很小，可以忽略不计。由图2根据基尔霍夫电流定律，可列写uap和uau的关系如下：

(2)

该数量关系对于整流侧同样适用，但应注意整流侧交流电流ia1=-ia2。对于uap和uau，还存在如下的数量关系：

(3)

式中：Nap和Nau分别为A相各桥臂开通子模块数量，UC为子模块电容电压值。由式(3)可以得出，MMC每相子模块开通数量之和恒定为N。因此使MMC每相各桥臂子模块开断数量按一定规律变化，可使每相上获得对应阶梯波。

2 DNCM控制器设计

2.1 控制方法

DNCM的控制思想是根据系统的运行状态和反馈的输出量计算所需的下一时刻输出电流参考值，再根据实测电流和参考电流的差值计算下一个控制周期开始时刻的子模块开通数量，当电流差值达到一定值后使电平发生跳变，从而使交流侧实际电流不断逼近参考电流。系统的整体控制流程如图3所示，可分为三部分。对于两侧MMC而言，计算子模块通断数和生成触发脉冲环节大体一致，而计算参考电流环节有所不同。

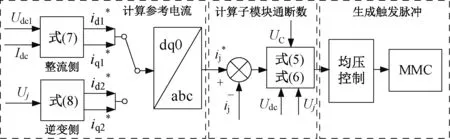
图3 系统整体控制框图Fig.3 Overall control block of the system

设T为控制系统的调制周期。由于T很短，故可认为在稳态下变换器电流和电压均不会发生突变。故在第k个控制周期Tk中，将式(2)离散化，并令Udc2(k)、Ua2(k)分别为该控制周期下逆变侧输入直流电压和输出交流电压，ia2(k)为本周期内交流侧输出电流，ia2(k+1)为下一周期逆变侧希望输出的交流电流值。可得该周期中uap(k)和uau(k)的表达式为

(4)

由式(4)可知，uap在本周期内的计算值取决于ia2在下一控制周期内的值。因此选取适当的ia2(k+1)的值，即可使交流侧输出电流跟随参考值变化。将ia2(k+1)替换为交流侧电流的参考值ia2*，即可使各桥臂子模块开通数量的变化规律跟随参考电流规律，从而达到电流逼近的目的。此时令Njp(k)和Nju(k)分别为某一控制周期内整流侧上j相上、下桥臂子模块开通数，Uj(k)与UJ(k)分别为整流侧和逆变侧各相交流电压，ij(k)和ij*分别为整流侧各相电流及其参考值，NJp(k)和NJu(k)分别逆变侧各相上、下桥臂子模块开通数，iJ(k)和iJ*分别为逆变侧各相电流及其参考值。结合式(3)和式(4)，可以分别列写出整流侧和逆变侧任意桥臂上开通的子模块数分别为

(5)

(6)

对于上式中的ij*和iJ*，还需根据其所在侧进行分类讨论。对于整流侧MMC，为保证直流侧输出的稳定，本文参考电压源换流器的经典控制策略，对直流电流和直流电压利用PI控制器分别得到参考电流的d轴和q轴分量，其表达式分别为

(7)

式中：Udc_ref和Idc_ref分别为直流侧电压和电流的参考值；Udc1和Idc分别为整流侧MMC直流出口处的电压和电流的测量值。综上，可得到整流侧MMC控制系统如图4所示。

图4 整流侧MMC控制系统Fig.4 Control system of rectifier MMC

对于逆变侧MMC，可采用电压源换流器经典控制理论中的解耦控制对交流电压进行解耦计算得出所需的电流参考值。令isd*、isq*分别为参考电流值的d轴和q轴分量，Ps*、Qs*为有功和无功功率参考值，Usd和Usq分别为逆变侧交流电压测量值的d轴和q轴分量，其计算公式为

(8)

经过式(8)的计算，交流电压转变为参考电流的各分量，同时在计算过程中不需要PI调节器，使系统对调节参数的依赖程度有所降低。因此可得逆变侧整体控制系统如图5所示。

图5 逆变侧MMC控制系统Fig.5 Control system of inverter MMC

在两侧MMC控制器计算得出子模块开通数量后，还需结合适当的均压策略才能得到相应的触发信号。文献[20]对其提出的无差拍控制的电流和电压波动范围进行了定量分析，本文将参考其分析方法，对DNCM通过电流误差控制电平跳变的原理进行分析，再根据分析结果选择适当的均压方法。

2.2 DNCM控制原理

为便于分析，本文以逆变侧A相上桥臂为例进行分析，其他各桥臂以此类推。取式(2)中的上桥臂电压表达式，并进行积分，可得逆变侧A相电流ia2表达式为

(9)

同理，若将上式中的ia2*替换为A相参考电流ia2*，将uap替换为A相上桥臂参考电压uap*，则可得

(10)

令式(9)、(10)相减并变形，可得

(11)

根据式(11)分析可知电流误差Δia和电压修正量Δuap间为正比关系，同时由于Leq的单位通常为mF，而T仅仅为几十μs，因此较为细微的电流误差也会被放大。故在任意电平区间内，若Δia超过某个阈值，则此时的Δuap将足以引起电平切换，从而降低该电平的持续时间。

接下来讨论Δia和Δuap的变化区间，及电流误差对输出电平数修正的过程。由于DNCM与NLM均属于阶梯波调制，故二者产生阶梯波所需电平数的取整原理相同。图6为某一电平区间前后A相上桥臂电平发生切换时的示意图，图中Np代表阶梯波在某一电平区间内的电平数，调制后输出的阶梯波与正弦波参考波已分别在图中标出。

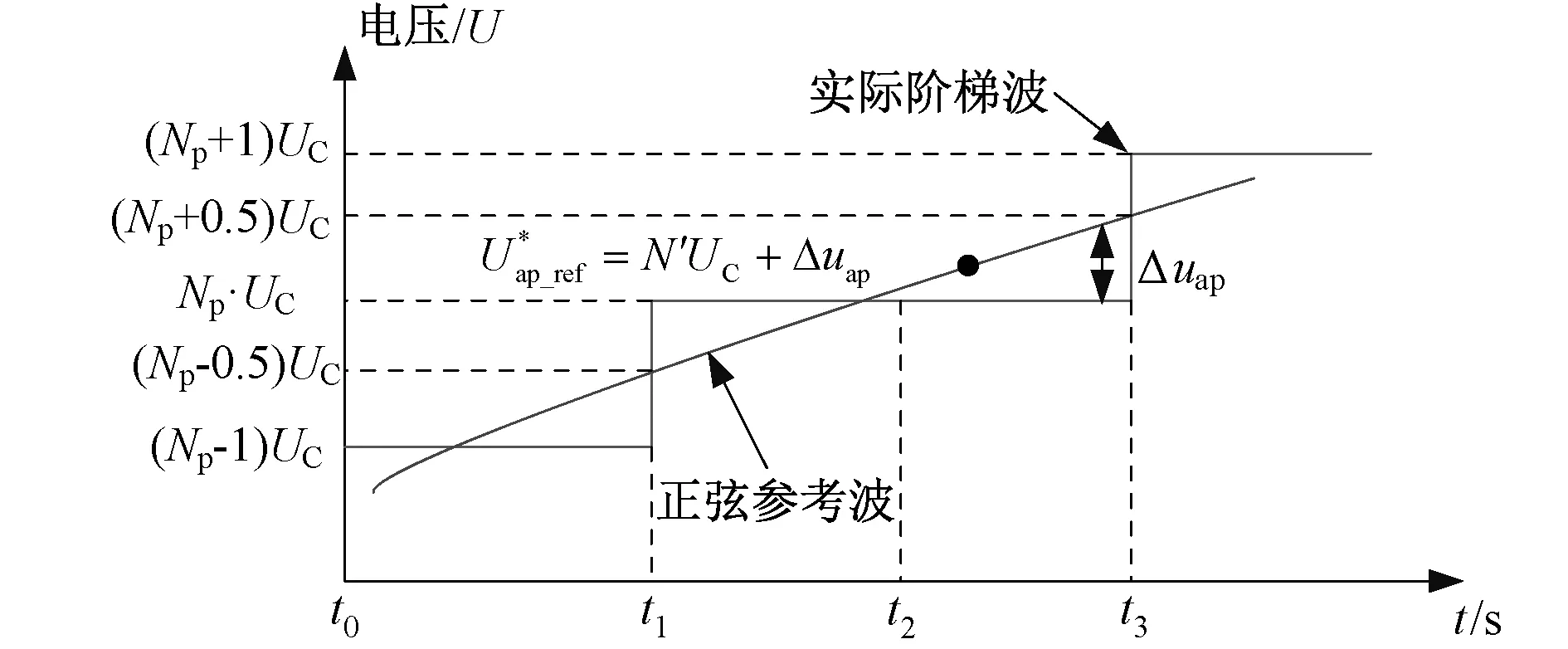
图6 电平切换Fig.6 Switching of level

设t1-t3内子模块开通数量均为N′，则从图中不难发现，上桥臂子模块开通数量分别在t1和t3时刻达到临界点，在t1时刻有N′=Np-1，t1-t3内有N′=Np，t3时刻有N′=Np-1。则在t2时刻可得正弦参考波和阶梯波之间的数量关系为

(12)

在t1和t3时刻，根据NLM的调制原理可得

(13)

(14)

根据取整函数round(x)的性质，根据式(13)和式(14)可得Δuap的极大值Δuap_max和极小值Δuap_min分别为

(15)

(16)

而由式(11)可知，电流误差与电压修正量成正比，故在t2时刻若存在Δia使Δuap≥Δuap_max，可得

(17)

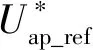
设Δia的上限和下限分别为σmax和σmin，则根据式(11)、式(13)和式(14)可得σmax和σmin的变化区间为

(18)

综上，A相电流误差的变化区间为

(19)

分析式(19)可知，电流误差的阈值仅取决于控制周期、子模块电容电压参考值和等效电感值，与其他因素无关。因此即使在电平数量较少的情况下，DNCM对交流电流质量的改善作用也依然存在。实际上，NLM也同样存在电流误差，但其电平切换机制是通过对参考正弦波与子模块数之比进行取整实现的，电流误差无法反馈到电压增量中，电流的质量取决于子模块个数。通过电流误差选择电平数，是DNCM不同于NLM的关键所在。

由于DNCM调制下参考电流与实际电流波形相交但不重合，因此可认为DNCM具有滞环特性，且环宽取决于电流误差的限值。DNCM下逆变侧A相上桥臂电流误差与电平切换如图7所示。

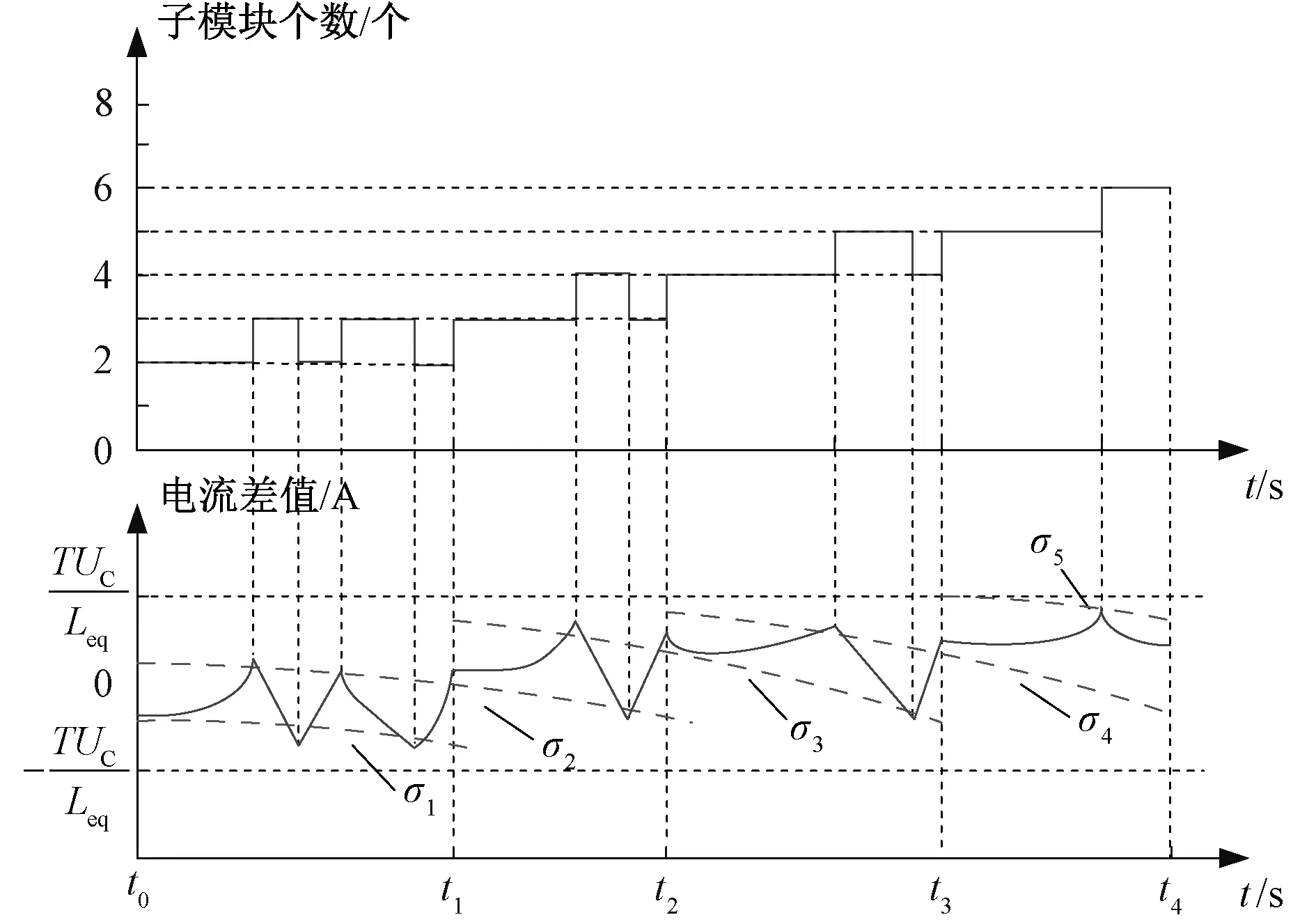
图7 DNCM下电平切换与电流误差Fig.7 Level switching and current difference with DNCM

图中子模块个数变化曲线根据所在电平区间分为4个区间，虚线σ1-σ5分别为电流差值在当前电平区间内的限值。以t0-t1区间为例进行分析，从图中可以得出电流误差对电平数的修正过程为：在t0-t1区间内可得σmax=σ2及σmin=σ1，当电流误差在本电平持续时间内超过σmax时，在滞环特性的作用下，电压修正量会使电平调节启动，进而增加1个电平，从而将电流误差控制在滞环环宽范围内，当电流误差低于σmin时同理；在t1时刻虽然电压误差再次超过上限，但由于即将进入下一电平区间，故电平修正机制未启动，而σmax和σmin也将变为σ3和σ2。综上所述，σmax和σmin在每个电平区间内都不完全相同，本区间内的σmax将在下以区间内变为σmin，但均只会在滞环环宽内波动。

值得一提的是，系统稳定运行时各正弦周期内各电平区间中电平仅在[Np,Np+1]或[Np-1,Np]中变化，不会在同一个电平区间内发生在[Np-1,Np+1]区间内变化的情况。以上升沿为例，某电平区间内电平数在[Np-1,Np+1]区间内变化及对应的电流差值变化趋势如图8所示。

图8 电平数和电流差值变化趋势Fig.8 Trend of level and current difference

由图可知，正弦参考波在t0-t5时刻均处于Np电平区间内，t5时刻电平区间由Np切换至Np+1。可以看出，若将子模块个数转化为桥臂电压，则在t3-t4时间内，根据式(11)和式(12)可得

(20)

式中：Usin*为正弦波在t3-t4内对应的参考值；Δu为电压修正量。由式(20)可得，此时的电压修正量已远超过其允许的波动区间，同时Δi的值也已越过σmin且没有进行修正，这在稳态运行条件下具有滞环特性的DNCM是不可能发生的。当电压处于整体下降趋势时，该结论依然成立。

2.3 子模块电容均压控制

由于DNCM改善电流的方式是增加电平切换次数，没有考虑子模块的运行状态，故子模块开断频率相比NLM有所增加，进而导致变换器整体损耗增加。因此在选择均压方法时，应尽可能选择降频排序方法。

本文采用文献[21]所提的双因子均压方法，这种方法通过引入子模块电容电压的上、下限Umax、Umin和两个保持因子M1和M2，使各子模块在每个调制周期内尽可能保持当前的工作状态，从而达到降低子模块开关频率的目的。两个保持因子应满足如下关系：

(21)

以上桥臂为例，双因子排序方法的流程如图9所示。在当前控制周期开始时刻，若上桥臂电流ijp方向为正，则子模块将在电流的作用下进行充电，则将原先已经处于投入状态的子模块的电容电压Usm乘上一个略小于1的保持因子M1；若桥臂电流方向为负，则将原先已被切除，电压低于所设下限的子模块乘上一个略大于1的保持因子M2后，再使用NLM排序法(冒泡法)进行排序，下桥臂以此类推。这样虽然会使各子模块电容电压波动幅度增加，但可以使全部子模块在下一次触发脉冲中尽可能保持现有工作状态，从而达到降低子模块的开关频率的目的。

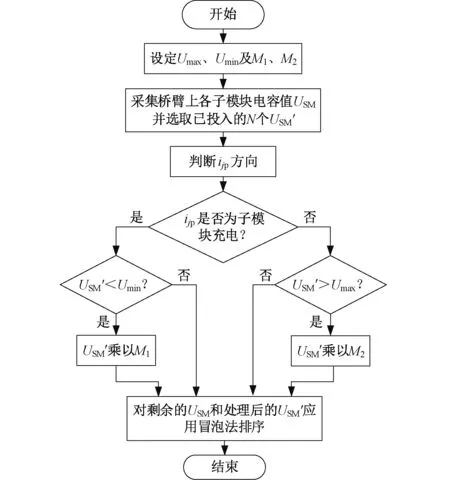
图9 子模块均压流程Fig.9 Process of voltage sharing of sub-modules

3 仿真验证

为了验证本文所提MMC-MVDC系统中的DNCM调制策略的有效性，在Matlab/Simulink中搭建了9电平MMC-MVDC系统的仿真模型。系统部分仿真参数如表1所示，其中两侧MMC及交流电网部分参数一致，表中不再重复给出。

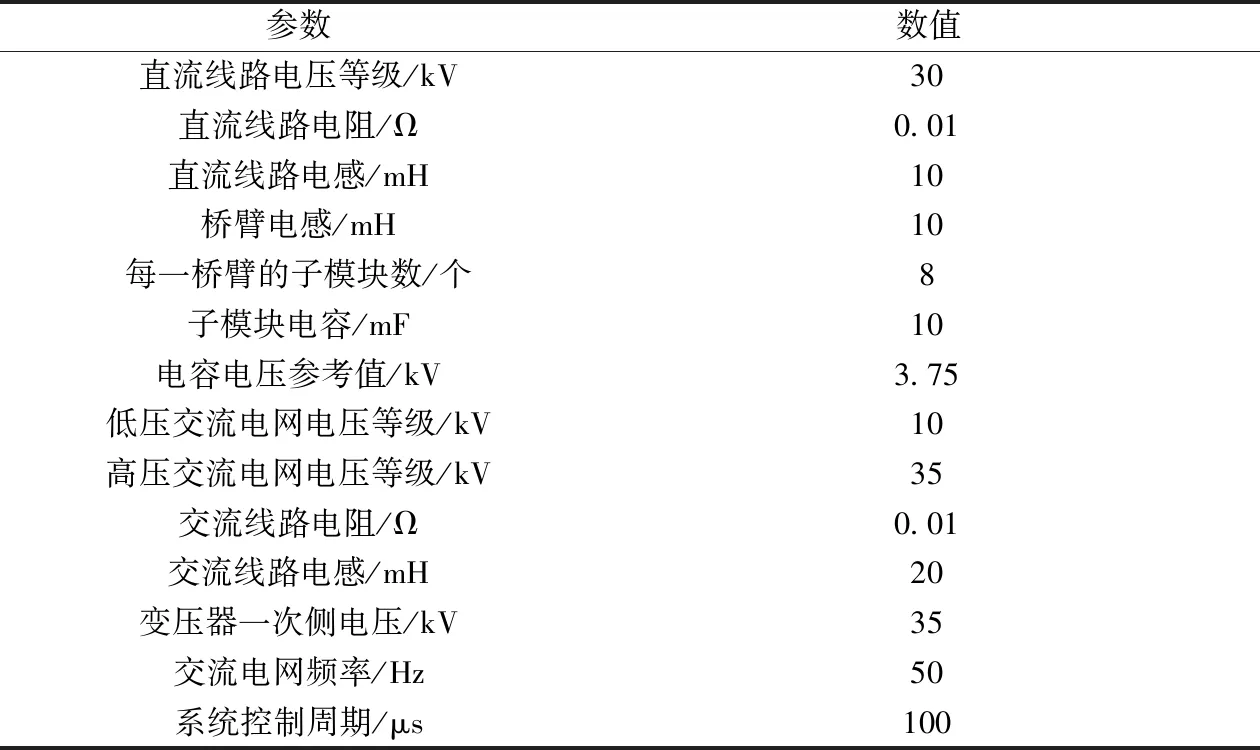
表1 仿真参数Tab.1 Data of simulation

3.1 滞环特性仿真

DNCM控制策略下逆变侧A相交流侧输出电压和电流波形分别如图10(a)和图10(b)所示，整流侧整体变化趋势与逆变侧类似，故不再单独列出。可以看出，DNCM控制下，由于对参考电流进行了实时跟踪，在各电平区间内电平均发生多次跳变，且跳变的次数不统一。同时，电压的多次跳变使电平切换得以平稳过渡，从而使输出电流波形更加逼近正弦波，从而降低交流侧的谐波含量，提升电能输出质量。

图10 DNCM下MMC输出电压Fig.10 Output voltage of MMC with DNCM

DNCM下逆变侧A相上桥臂电平数量波形和对应的电流误差波形分别如图11(a)和图11(b)所示，其部分波形(以虚线标出)分别如图11(c)和11(d)所示。结合图(a)和图(b)可知，在滞环特性的作用下，电流误差的细微波动会反馈到电压中，进而导致电平的切换，且电流误差的整体变化趋势与电平的整体变化趋势相同。同时从图(b)中不难发现，A相电流误差在[-1.5A，1.5A]内波动而不越限，与2.2节中的理论公式相符；图(a)中电平波形各正弦周期内上升阶段各电平区间中电平仅在[Np,Np+1]中变化，下降阶段电平的变化区间为[Np-1,Np]，并没有出现[Np-1,Np+1]的情况。而且，在图(c)中t1-t2时间段内所在电平区间的电平数为4，结合图(d)中电流误差的变化趋势可知，电流误差以σmax和σmin为边界在电平调节机制作用下对电平数进行修正，且电平切换时刻与电流误差越限时刻一一对应，与2.2节中的理论分析完全一致。

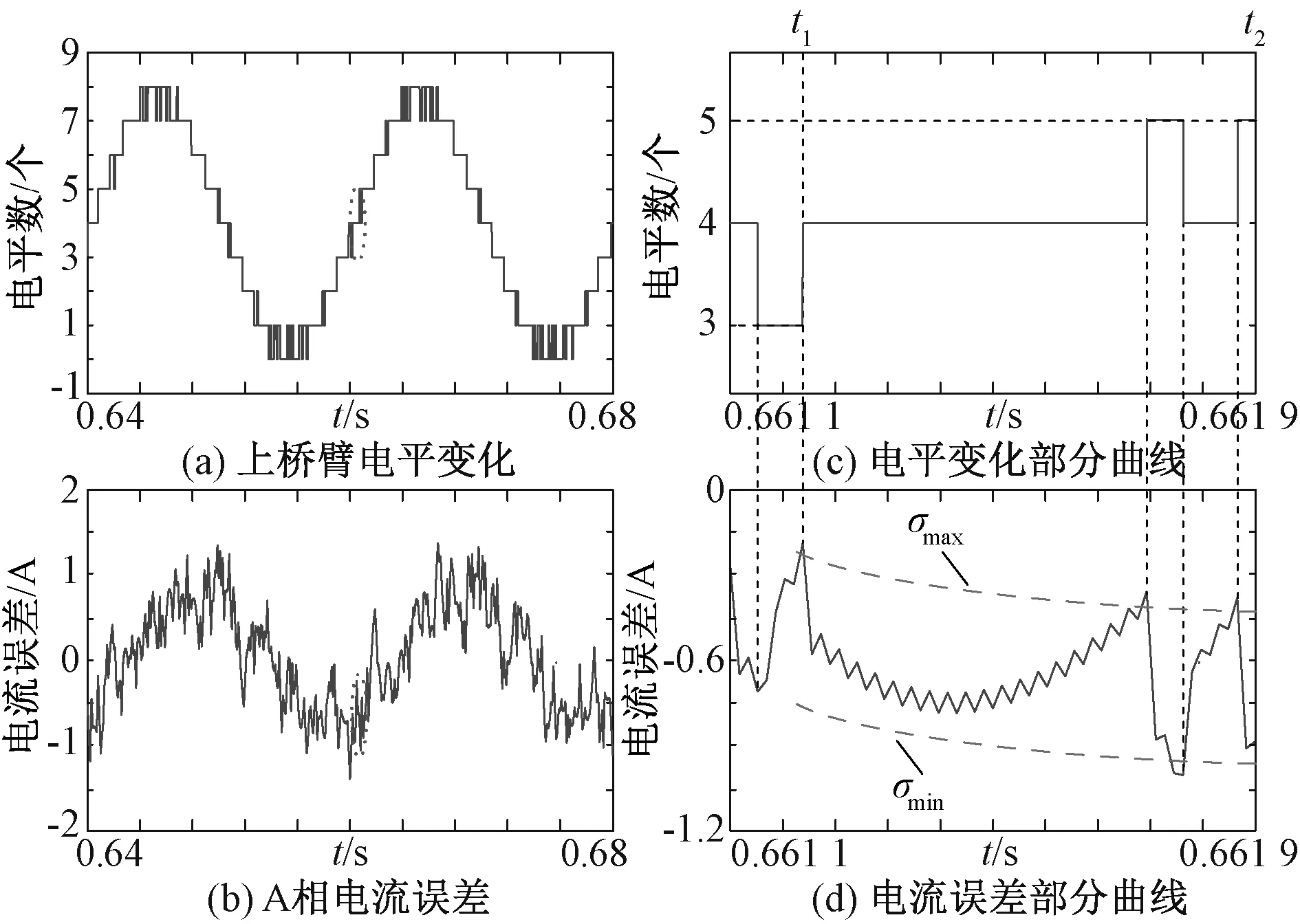
图11 A相上桥臂输出电平和电流误差Fig.11 Output level and current difference on upper bridge arm of phase A

3.2 谐波特性仿真

图12为两种传统控制和DNCM下的交流电流FFT分析结果。从图中可知，由于电平数量较少，NLM调制下THD含量为7.94%，谐波以奇数次谐波为主，其中5次谐波含量最高；由于电平切换数量很高，CPS-PWM调制下THD含量相比NLM大大降低至1.52%，虽然和NLM类似，谐波以奇数次谐波为主，但相比NLM高次谐波在谐波的总比例有所提高；无差拍调制下THD含量为1.4%，相比传统控制策略奇数次谐波含量大大降低，谐波以偶数次谐波为主。综上所述，在MMC子模块数较少的情况下，电平切换时的跳变会使交流侧输出谐波含量显著降低，而无差拍控制策略下对参考电流的跟踪会使电流畸变率进一步降低，大大提高交流侧输出电能质量。

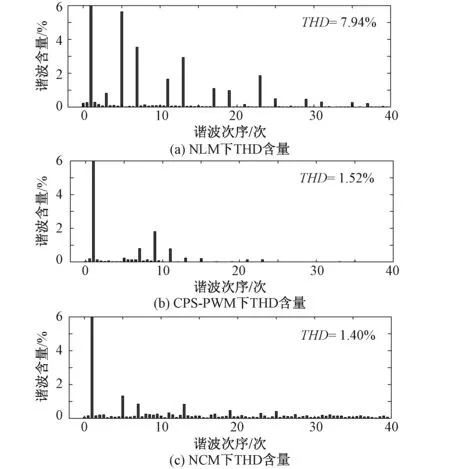
图12 三种控制策略下FFT分析结果Fig.12 Analysis results of FFT with three control strategies

图13为Leq、T和UC均不变的情况下，仅改变各桥臂子模块个数时DNCM下交流电流谐波含量变化曲线。由图可知，当桥臂子模块数量从8降低至2时，谐波含量总体增加了0.15%，并没有因为子模块数量的减少而大幅增加。因此可以认为，无论子模块数量多或少，DNCM均可以有效改善交流侧谐波畸变，其改善程度与子模块数量无关。

图13 DNCM下子模块个数与谐波含量的关系Fig.13 Relationship between number of sub-modules and harmonic content with DNCM

3.3 稳态运行仿真

图14为NLM和DNCM下1 s内A相上桥臂单个子模块的平均总开通次数，以反映各子模块的开关频率。其中图14(a)、14(b)分别为NLM和DNCM下的开关次数。由图可得，1 s末NLM的通断次数为450次，即平均开关频率为450 Hz。相比NLM，由于DNCM增加了利用电流误差调节电压增量的环节，开关频率有所上升，达到了556.45 Hz。而采用双因子均压控制后无差拍控制下的开关频率均值降低至491.25 Hz。因此，DNCM控制策略下子模块通断频率较低，当采用降频均压后子模块通断频率进一步降低，从而降低MMC的整体损耗。

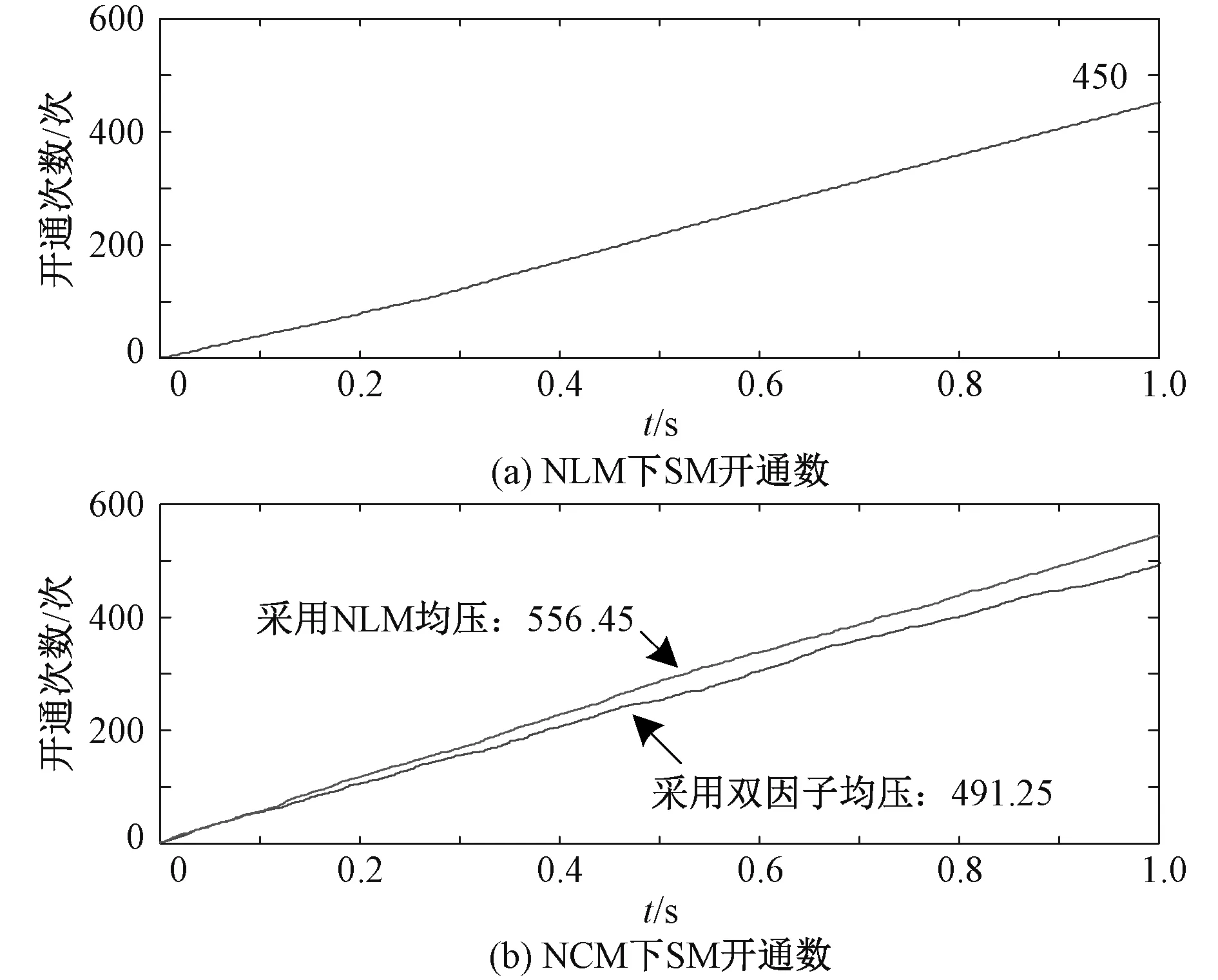
图14 两种控制策略下子模块开通次数Fig.14 Opening times of SMs with two control strategies

直流侧电压和电流波形分别如图15(a)和15(b)所示。从图中可以看出，图(a)中电压虽有小幅波动，但整体稳定在理论值30 kV附近，且振幅不超过±10 V，整体波动幅度在0.67%左右；受直流线路各参数影响，图(b)中电流在60 A左右波动，但波动幅度均不超过±2.5 A。因此可以认为，在MVDC系统中，DNCM可以使整流侧输出较为稳定的直流电压和电流，从而为逆变侧提供可靠的直流电源。

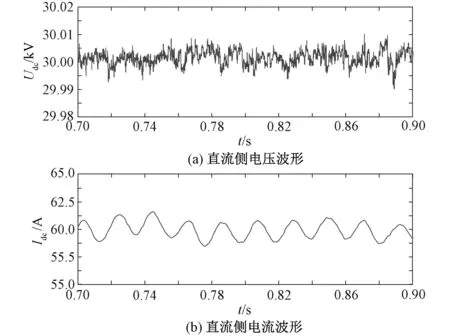
图15 直流侧电压和电流波形Fig.15 Voltage and current on DC side

图16为DNCM下逆变侧A相上桥臂各子模块电容电压波形，其中图(a)为采用传统NLM排序均压(冒泡法)的子模块电容电压，图(b)为采用双因子均压后的子模块电容电压。从图中可以看到，无论采用何种均压，子模块的电容电压均稳定在理论值3 750 V左右，电压波动幅度均低于±0.53%，基本满足MMC对子模块电容电压稳定性的要求。结合图14(b)分析，相比传统NLM排序均压，采用双因子均压后虽然电容电压的波动幅度略微增加，但是由于通过设置阈值并引入双保持因子使子模块尽可能保持当前的工作状态，子模块的通断频率得以降低，从而减小了变换器的总体损耗。

图16 各子模块电容电压Fig.16 Capacitance voltage of each SM

4 结 论

本文针对中压MMC因模块数量少而导致电流畸变率高的问题，提出了适用于MMC-MVDC的DNCM控制策略，得出结论如下：

(1)DNCM控制策略具有滞环特性，可通过相电流差值控制桥臂电压修正量，且二者之间成正比关系。电流差值的大小与等效电感、控制周期和子模块电压值有关，与其他量无关。

(2)在MMC-MVDC系统中，相比传统控制策略，DNCM控制可以有效降低交流侧谐波含量，且改善程度不受子模块数量影响。同时可以保证直流侧输出稳定的电压和电流。

(3)DNCM控制下的子模块开关频率相比NLM虽有所升高，但整体仍处于较低水平，同时MVDC系统中的直流侧电流和电压均较为稳定。相比传统控制策略，DNCM所需的PI控制和解耦控制环节更少，从而系统控制结构更简单，计算速度更快。