高弹性电网下考虑需求响应的多时间尺度优化调度策略
杭海燕,杨力强,甘 雯,孙 毅,杨泓玥,李泽坤
(1.国网湖州供电公司调度控制中心,浙江 湖州 313000;2.华北电力大学 电气与电子工程学院,北京 102206)
0 引 言
为应对日益复杂的经济形势和能源局势,国网浙江省电力有限公司首次提出建设能源互联网下的多元融合高弹性电网,旨在唤醒海量资源、增强源网荷储柔性互动,充分打造高承载、高互动、高自愈、高效能的电力网络,提升电网安全及运行效率[1,2]。
高弹性电网下多方资源的灵活调度是提高电网安全水平和提升电网运行效率的基础,已有较多文献考虑了需求响应(demand response,DR)与发电侧的协同调度,文献[3]考虑了需求侧的影响,考虑可中断备用与发电侧备用的协调优化,建立了计及用户侧的发电日前调度计划,所提模型有效降低了发电成本。文献[4]将可中断负荷作为虚拟机组考虑进日前调度计划中,考虑了价格性DR对发电计划的影响,可有效与常规机组进行配合,降低机组的运行成本。文献[5]结合风电、慢机、快机以及价格型和激励型DR,构建了“日前-日内-实时”多时间尺度滚动调度计划模型。文献[6]从价格型和激励型DR的角度分析柔性负荷在实际响应中的不确定性,结合常规机组和风电构建了日前-日内-实时的协调调度模型。考虑用户侧互动下将发电侧和需求侧的资源进行综合规划有利于电力系统的安全经济运行,有必要将用户响应纳入发电调度,并增强与用户侧的互动从而统一优化发电侧和需求侧资源。文献[7]考虑了DR和线路可靠性,结合负荷预测的确定性,建立日前-实时两阶段风险调度模型,但未结合具体的灾害场景进行分析。上述文献主要针对考虑DR的多时间尺度发电调度计划开展研究,面向常规场景已有较全面的工作,但针对极端灾害场景的研究还较少。
对于极端天气条件下的电力系统风险评估,建议采用一些考虑天气相关停电引起的潮流变化的可靠性分析模型[8],大多数文献集中在线路停电概率计算、提供备用容量等方面去提高调度的安全性。针对台风灾害,文献[9]考虑了飓风场的影响,提出一种规避风险的最优潮流模型,以发电成本和风险成本总和最小为目标函数,并开发电网的地理空间模型用于输电线路停电概率的计算。文献[10]针对高概率突发事件,以事故前系统成本最优为目标函数建立安全最优潮流模型,获取在台风登陆前的最佳应急调控方案,有助于协调面对自然灾害时电力系统的经济性和安全性,可为调度人员提供有效的参考。就其他自然灾害而言,文献[11]分析了山火对电力系统运行的影响,以及风的存在对火灾的行为及其对线路的影响,以最小化系统发电成本与备用容量成本之和为目标函数,建立了山火对电力系统调度影响的概率最优潮流模型,以及时协调系统的调度和分配给每台发电机的储备量。文献[12]以系统的发电成本为最小目标考虑电力系统有功功率最优分配,以电力系统发电成本和切负荷损失最小为目标评估交/直流潮流的最优切负荷评估模型,对洪涝灾害下的电力经济损失进行评估。以上文献考虑了自然灾害对电力系统造成的线路故障和经济损失,但未考虑需求侧用户参与电力系统调度运行。
本文针对台风灾害下的多时间尺度调度问题,考虑DR的参与,根据激励型DR的不确定性建立其成本-容量模型和机组等效出力模型。通过引入台风灾害下线路故障率的计算,以支路过载严重度为系统风险指标,以机组运行成本和DR成本为综合成本,构建了高弹性电网下考虑DR的多时间尺度优化调度模型,实现台风灾害下电力系统安全性与经济性的统一。最后以IEEE-30节点系统为例来验证所提方法的科学性及有效性。
1 台风灾害预报与DR时域协同调度架构
1.1 沿海地区台风灾害影响及预报机制分析
每年7月~9月,我国东南沿海地区易遭受极端台风灾害的影响,大多还会伴随暴雨、雷电等天气,会对负荷需求产生较大影响,引起明显波动,使其具有很大的随机性和不确定性。一般而言,若某区域离台风登陆点越近,该区域的负荷下降比例将越大。在台风登陆前后,天气将经历明显的三阶段式变化,各区域的负荷水平也会受其影响,给电力系统的安全稳定运行带来极大的干扰和波动。随着时间的推移,台风中心离开登陆区域后,其强度将会逐渐减弱,当减弱为热带低压时,气象部门将停止对其编号,并忽略其影响力。
在台风灾害下,尽管不同时期的负荷水平和负荷特性有所区别,但台风期间的日最大负荷变化具有一定规律性。台风移动速度快,登陆后强度迅速减弱[13],但是因台风造成的降雨通常会持续一到两天,这将对夏季的持续高温造成直接影响,受台风灾害影响的区域范围内温度会降低3~5 ℃,负荷会因居民使用空调的频率减少等原因产生较大幅度的下降。据统计,在台风灾害期间,至少有一天的温度会较前一天有显著变化。
1.2 考虑DR的多时间尺度协同调度架构
本文提出台风灾害下电力系统日前调度和日内调度两阶段调度策略,其结构框图如图1所示。
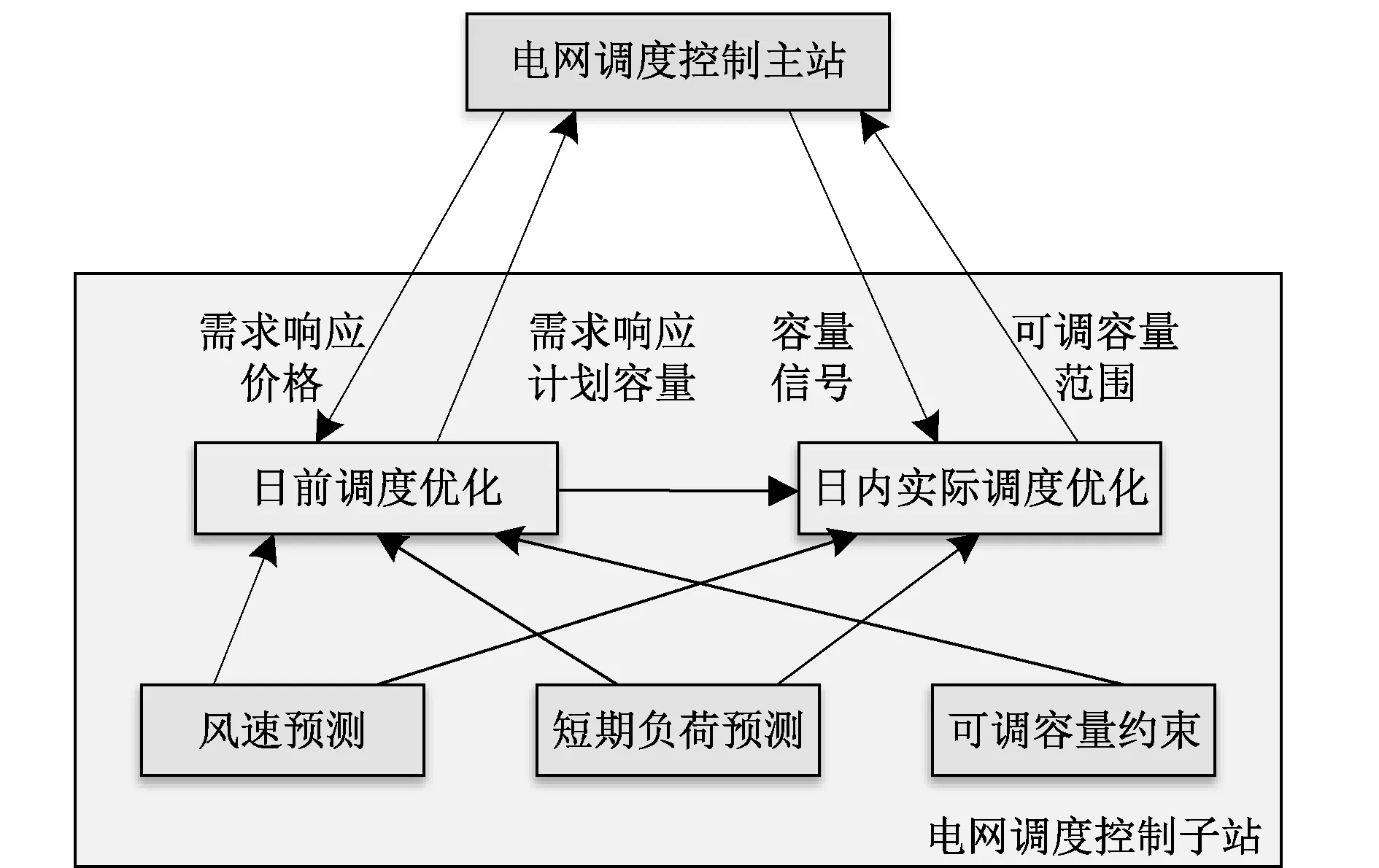
图1 考虑DR的多时间尺度的协同调度架构Fig.1 Multi-time scale collaborative dispatch architecture considering DR
(1)日前调度优化
在日前调度时,对台风期间的日负荷进行预测,根据风速预测数值对线路故障率进行计算,对电力系统潮流进行计算,以机组运行成本和DR成本的综合成本最小为目标函数,建立日前调度优化模型,求解得到日前机组调度计划和DR计划容量。
(2)日内调度优化
在日内调度中,根据短期风速预测数据计算线路实时故障率,对电力系统网络结构进行调整,记日内调度总负荷为短期负荷预测数值与DR计划容量的差值,在此基础上考虑DR的不确定性,以综合成本最小为目标函数,建立日内调度优化模型,求解得到日内机组调度计划。
2 台风经停全时间尺度下的DR模型
2.1 DR成本-容量模型
负荷侧的DR可以分为激励型DR和价格型DR,其中激励型DR是指电力公司通过制定相应的价格补偿策略,激励用户在系统可靠性受到影响时及时响应执行及削减负荷。通常由用户与DR实施机构签订合同,在用电高峰期或低谷期由电力公司向用户发出响应信号,用户接到响应信号后未进行响应的用户将受到惩罚。用户与电力公司签订的合同一般包括:用户削减容量、削减持续时间、提前通知时间、负荷削减最小时间间隔、补偿单价、惩罚单价等。
在实际调用过程中激励型DR的不确定性主要由用户基线负荷预测的不确定性和用户响应过程中出现的偏差所致,而用户响应偏差受设备故障和用户的实际响应情况影响[14]。负荷预测中的不确定性是不可避免的,经常认为负荷预测误差符合某种概率分布;当系统调度员向用户发出命令时,用户应自觉地做出响应。合同中补偿价格可激励用户履行合同积极响应,惩罚价格可提高合同约束力,降低用户违约概率。但用户的实际响应情况受用户对响应效益理性判断、次日突发状况和用户响应信誉的影响,使得用户的响应行为具有不确定性。
激励型DR的成本为其容量的二次函数:
(1)
式中:k为用户舒适度;qt为DR容量;A1、A2分别为响应成本二次函数的系数。
2.2 考虑DR不确定性的机组等效出力模型
现有的研究通常认为激励型DR按照合同方式实施,由于用户的实际响应情况受用户次日突发状况等影响,具有一定的不确定性,所以允许实际响应容量在合同允许的比例范围内波动。
若按DR计划量执行调度计划,其不确定性将由发电机组进行功率缺额补充:
PG,actual(t)=PG,forecast(t)+ε(t)
(2)
式中:PG,actual(t)为t时刻的系统实际总负荷;PG,forecast(t)为t时刻的系统预测总负荷;ε(t)为负荷预测误差。
由于用户响应不确定性,实际执行的响应总负荷与要求执行的响应总负荷之差是随机量,采用充足的历史数据可对用户实际负荷的预测误差进行估计,一般认为其服从正态分布[15],ε(t)~N(0,σ(t))。同时,激励型DR在调用过程中满足负荷削减量上下限约束。
(3)
3 台风灾害下的多时间尺度优化调度策略
3.1 线路故障率的计算
根据我国东南沿海某省台风灾害后的实际破坏情况,台风来临时,随着风速的增加,杆塔的故障率将大大增加。同时,输电网故障均为结构性失效,例如倒塔、断塔等。采用指数型曲线函数来拟合台风风速vs与杆塔s失效率λs关系[10,16],具体指函数表达式为
(4)
式中:vmin为杆塔设计风速;模型系数H取值为0~0.4。
参照可靠性评估理论中的元件失效概率计算,可知单个杆塔的故障概率ps为
(5)
考虑到实际电力系统运行中,一条输电线路上有多个杆塔,根据串联系统可靠性评估理论,可求得整条线路的发生故障的概率为
(6)
式中:Nk是线路k上的杆塔数量。
根据线路故障率的数值大小对电力系统网络进行相应参数和结构调整,参与多时间尺度优化调度计算。
3.2 系统运行风险计算
风险是对不确定运行场景的发生概率与严重程度的综合度量[17]。目前很多研究都针对电力系统的运行安全和风险进行预测,风险评估则是对预测的结果进行评估,获取各类系统运行风险的数值。针对电力系统的实际情况,其风险的数学表达式为[17]:
(7)
式中:NC为预想故障集;Pr(k)为下一个时段第k个预想故障发生的概率;Sev(k)为第k个预想故障发生后系统损失的严重程度。
本文选用支路过载严重度作为风险指标,支路过载可能引发系统发生连锁故障支路过载严重度函数是针对每个电路(传输线或变压器)定义的,电路中潮流占额定值的百分比则为该电路的过载严重程度,采用连续型函数计算不同故障下的支路过载严重度[18]。系统发生故障后,支路i的支路过载值ωLi为
(8)
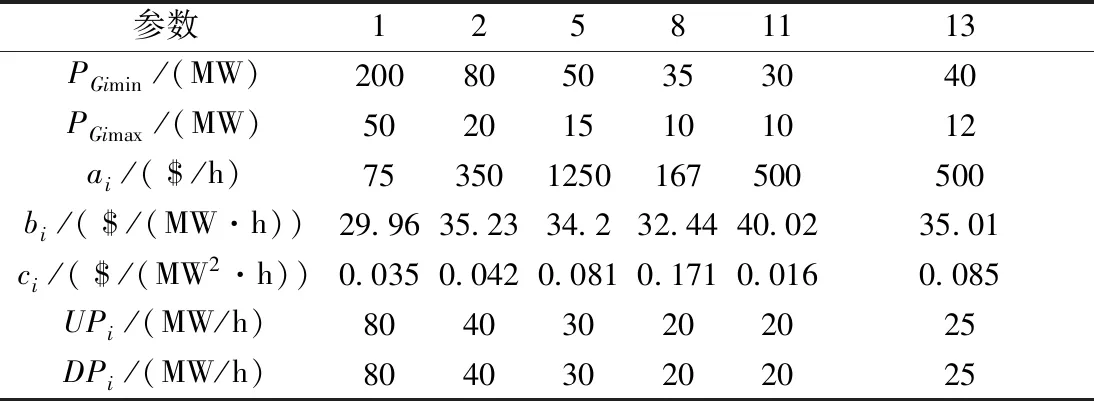
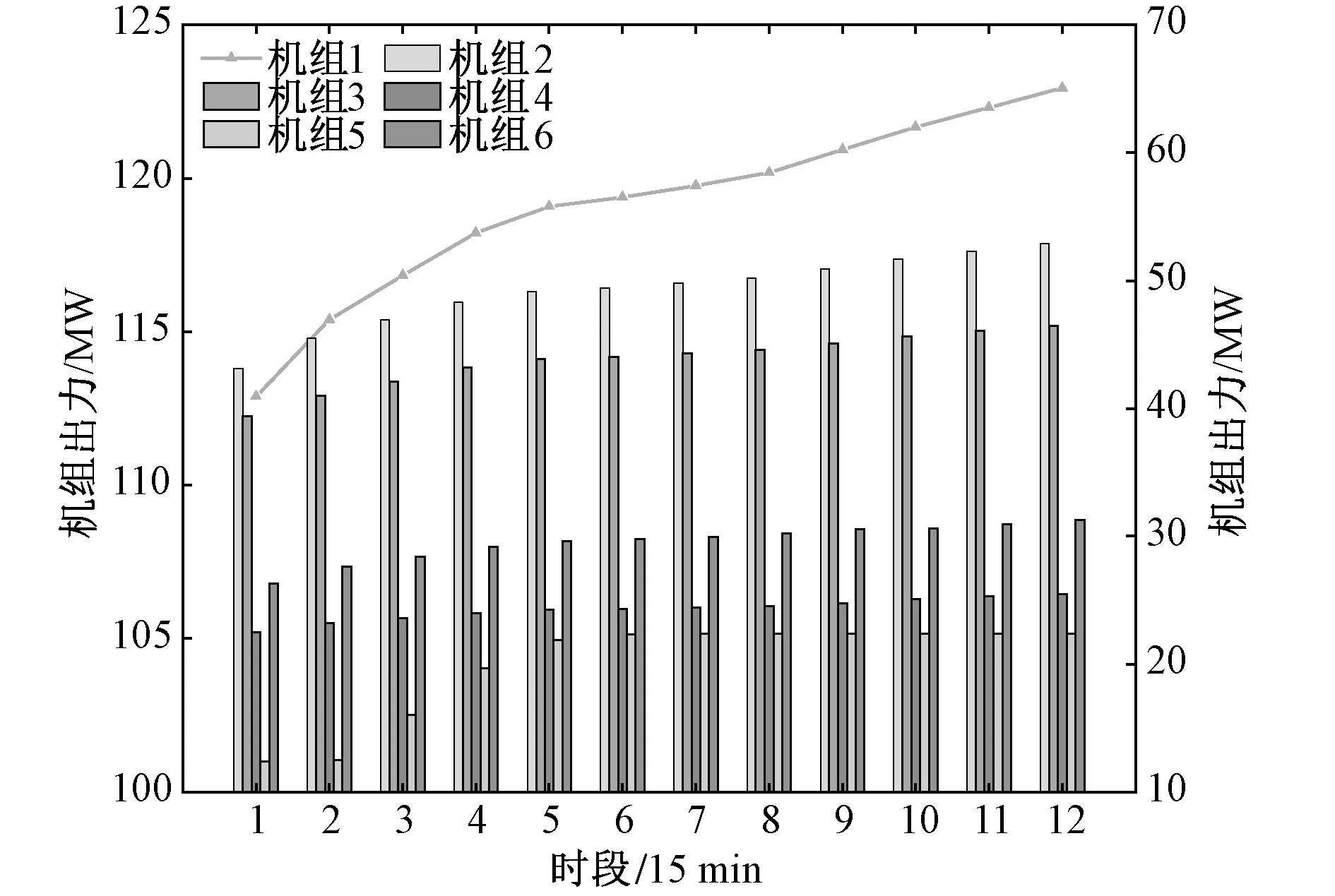
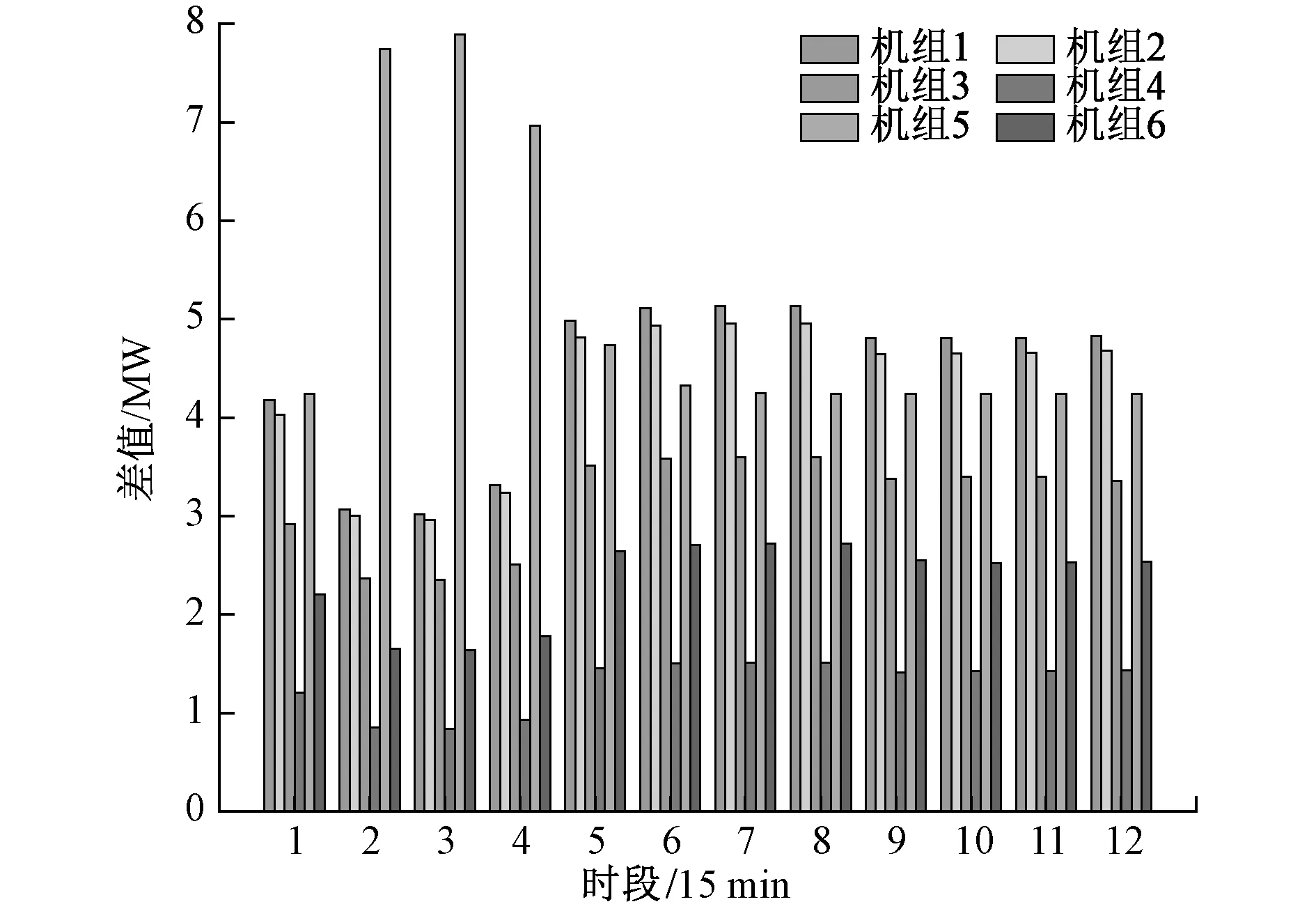
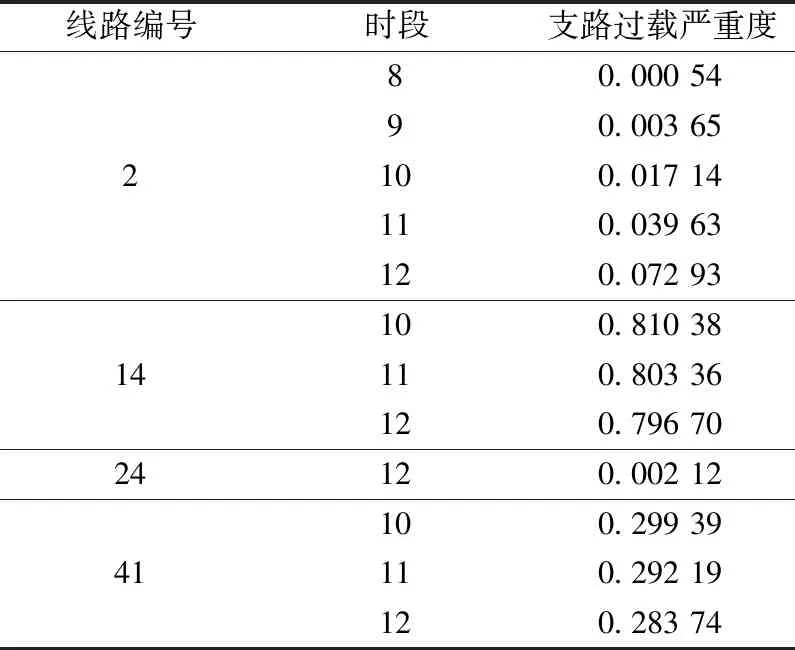
式中:Li为支路i的实际输送功率与功率越限额之比;L0为设定的阈值,本文取0.9。当Li 通过计算全部支路过载指标,可得到系统支路过载严重度Sev,其定义为 (9) 通过对台风风速的提前预测,可计算出相应的实时线路故障率,将此故障率记为式(7)中的某一个预想故障发生的概率Pr(k)。 系统运行风险指标的计算流程如图2所示。 图2 系统运行风险指标计算流程图 Fig.2 System operation risk index calculation flow chart 3.3.1 日前调度优化 本文在电力系统日前调度阶段以1 h为单位分段,将一天分为24个时段。以机组运行成本和DR成本之和最小为目标函数,其数学模型如下所示: (10) (11) 式中:T为整个调度期间内调度时段的个数;PGi,t为第i台机组在t时段内的有功出力;ai、bi、ci为其耗量特性曲线参数。 日前调度优化需要满足的约束如下。 (1)系统约束: (a)功率平衡约束 首先要保证网络中各节点的功率平衡: (12) 式中:PGi,t、QGi,t为第i台机组在t时段内的有功、无功出力;PDi,t、QDi,t为节点i在t时段的有功、无功负荷;Vi,t、θi,t为节点i在t时段的电压幅值与相角,θij,t=θi,t-θj,t;Gij、Bij为节点导纳矩阵第i行第j列元素的实部和虚部。 (b)节点电压约束 为了保证系统电压的稳定和系统元件的绝缘可靠性,必须使系统中各节点的电压保持在合理范围内,且不超过一定的限值: Vimin≤Vi,t≤Vimax (13) 式中:Vi,t为节点i在t时段的电压;Vimin、Vimax分别为节点i的电压上下限。 (c)线路潮流约束 当线路的传输功率超过一定范围时,线路的静态稳定性将受到破坏。为确保系统能够安全稳定运行,线路的传输功率不得超过其极限值: Pijmin≤Pij,t≤Pijmax (14) 式中:Pij,t为线路i-j在t时段内的有功传输功率;Pijmin、Pijmax分别为线路i-j的有功传输功率上下限。 (2)机组约束: (a)传统发电机组出力约束 PGimin≤PGi,t≤PGimax (15) 式中:PGimin、PGimax为第i台发电机组的出力上下限。 (b)机组爬坡速率约束 (16) 式中:ri,up和ri,down分别为第i台机组的爬坡率上、下限值,ΔT为每个调度时段的时长。 (3)DR容量约束 qmin≤qt≤qmax (17) 式中:qmin、qmax分别为DR容量的上下限值。 3.3.2 日内调度优化模型 目前电力系统实时调度以15 min为间隔,气象部门启动灾害天气3 h滚动预报预警机制,本文在实时调度阶段以15 min分段,将3 h分为12个时段。在日前调度优化中确定了DR计划容量后,考虑实际运行中DR的不确定性和负荷预测的不确定性,确定日内调度中各时段的总负荷。本阶段目标函数与日前调度时一致,由于各时段DR容量已确定,不再考虑其上下限约束,其他约束条件与日前调度一致。 本文的具体实施流程如图3所示。 图3 考虑需求响应的多时间尺度优化调度流程图Fig.3 Multi-time scale optimal dispatch considering DR flow chart 本文参考台风“天鸽”的基本信息[19],针对某地进行研究,设定该地区采用了修改后的IEEE30节点系统,接线图如图4所示,各机组及需求响应成本参数见附录A表A1[20]、表A2所示。设置杆塔设计风速为35 m/s,各线路年平均故障率见附录A表A3,在此假设台风正在接近线路15-23。 表A1 机组参数表Tab.A1 Unit parameters 表A2 需求响应成本参数Tab.A2 Demand response cost parameters 表A3 IEEE30节点系统线路年平均故障率Tab.A3 Annual average failure rate of IEEE30-node system 图4 台风路径和IEEE30节点接线图Fig.4 Typhoon track and IEEE30-node system diagram 通过matpower7.0的计算,日前各时段各发电机组的预期出力值如图5所示,由此可对系统进行日前调度。由于各机组的出力上下限值的不同,机组1在此电力系统运行调度中为主要出力机组;相较区域2,区域1与区域3的交互更多,位于区域1内的机组将在台风风速变化较大时承担更多出力,机组2的增幅明显大于机组3和机组4。同时,随着台风临近线路15-23,区域3内机组5附近线路受影响较大,出现潮流转移,机组6增加出力以维持该区域内的负荷稳定。 图5 日前调度各时段各机组出力预期值Fig.5 Expected output value of each unit during each period in day-ahead dispatch 日前调度优化中DR容量的变化与系统总负荷的变化趋势相一致,由DR分担一部分总负荷值,减轻各机组的出力压力。当风速逐渐减弱时,线路运行恢复稳定,运行风险降低,各机组出力趋于稳定,DR需求逐步减小。由于机组出力和DR容量与总负荷的变化有关,综合成本的变化趋势与总负荷的变化相一致。日前调度中各时段系统DR容量和综合成本如图6所示。 图6 日前调度各时段DR容量和综合成本图Fig.6 DR capacity and comprehensive cost during each period in day-ahead dispatch 模拟3 h内每隔15 min的风速数据,记为时段1-12。对应计算出线路故障率p,如表1所示。 表1 线路实时故障率Tab.1 Real time failure rate of line 根据式(5)可知,当风速v1小于杆塔设计风速vmin时,实时线路故障率为0,因此在实时调度中将时段1~4记为正常天气下考虑线路故障的情况,采用线路故障率的历史统计值进行计算,即线路年平均故障率。时段5~12记为台风灾害下考虑线路故障的情况,采用线路实时故障率进行计算。 假设当线路故障率大于80%时,采取断开线路的方式调整线路结构,根据日前确定的DR容量值,结合其不确定性,对所有机组出力之和进行调整,通过计算可以得出各时段机组的预期出力值对系统进行日内调度,此场景记为场景1,如图7所示。 图7 日内调度各时段各机组出力预期值Fig.7 Expected output value of each unit during each period in day-in dispatch 针对日内调度,设置DR不参与调度的场景(记为场景2)进行对比,计算场景2和场景1中各机组的出力值之差,场景2中的各机组出力均大于场景1,且在第2-4时段中DR容量主要承担了机组1、机组2和机组5的部分出力,如图8所示。 图8 场景2与场景1中各机组出力差值Fig.8 Differences of each unit output between scenario 2 and scenario 1 对比DR未参与系统调度时的场景,其各时段的系统综合成本与风险指标如图9所示,由于系统总负荷是确定的,综合成本变化趋势一致,其差值与DR的容量大小和容量-成本函数的系数有关。 图9 不同场景下的系统风险指标和综合成本曲线图Fig.9 Risk index and comprehensive cost curves under different scenarios 计算支路过载严重度时会出现潮流不收敛的情况,不同场景下的潮流不收敛次数如表2所示,有DR参与时出现潮流不收敛的情况较DR未参与系统调度时略好,且减缓了系统支路过载严重度的进程。 表2 不同场景下潮流不收敛次数Tab.2 Power flow non-convergence times in different scenarios 由于将系统最优潮流不收敛时的各线路潮流记为正常运行状态时的潮流,根据式(11)可得出其数值为1,由此计算出当系统最优潮流不收敛时,系统的支路过载严重度为系统的总支数,据此得到的系统风险指标主要受到潮流不收敛情况的影响,使得潮流收敛时计算出的支路过载值过小而无法体现。因此,对断开后潮流收敛的线路进行分析,不同场景下某线路断开后发生潮流不收敛情况的线路编号如表3、表4所示,不同场景下某线路断开后潮流收敛情况下的支路过载严重度如表5、表6所示。 表3 场景1中线路断开后潮流不收敛集合Tab.3 Non-convergence set of power flow after line disconnection in scenario 1 表4 场景2中线路断开后潮流不收敛集合Tab.4 Non-convergence set of power flow after line disconnection in scenario 2 表5 场景1中线路断开后潮流收敛时的支路过载严重度Tab.5 Line overload severity when power flow converges after line disconnection in scenario 1 表6 场景2中线路断开后潮流收敛时的支路过载严重度Tab.6 Line overload severity when power flow converges after line disconnection in scenario 2 针对线路25(即线路10-20,连接区域2和区域3)断开后的情形,在场景1中,时段1和2中系统处于正常状态,在时段3时系统出现过载情况,在时段4以后受风速及网络拓扑变化的影响,系统出现其它联络线过负荷,导致潮流不收敛,而在场景2中系统在时段2时即出现线路25断开后潮流不收敛的情况;针对线路2和线路24,在场景1中断开后系统均处于正常状态,未出现其他线路过载的情形,而在场景2中有过载情况发生;针对线路14和线路41,在场景1中线路断开后的系统支路过载严重度均低于场景2。可反映出在场景1中DR参与系统调度有利于系统安全性的提升,延缓系统部分风险的发生,及时采取补救措施。 本文针对高弹性电网在台风灾害下的多时间尺度调度问题,提出了一种考虑需求响应的优化调度策略。(1)通过对激励型需求响应不确定性的分析,建立了需求响应成本-容量模型,并结合实际情况的不确定性建立等效机组出力模型,通过有无DR参与的场景对比,可知在多时间尺度调度计划中考虑DR可降低系统的综合成本。(2)结合台风灾害下线路故障率的变化,提出以支路过载严重度作为风险指标进行系统风险评估,通过算例分析验证了考虑DR后,系统运行风险降低,尤其是台风高发区的风险,表明在多时间尺度调度计划中考虑台风灾害和DR的有效性。
3.3 多时间尺度优化调度模型

4 算例仿真
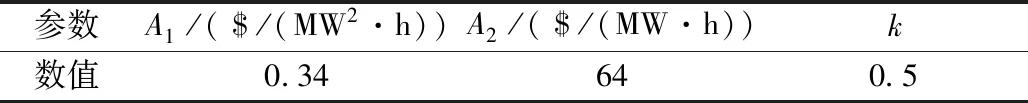


4.1 日前调度分析


4.2 日内调度分析






5 结 论

