考虑压密过程和残余强度的岩石统计损伤本构模型

潘有维，黄德文

(长江大学城市建设学院，湖北 荆州市 434023)

0 引言

岩石大多为两种或以上的矿物集合体，广泛地分布于大自然，是一种非均质非连续各项异性的材料，其内部含有大量的孔隙、裂隙、节理等缺陷。由于其破坏时具有复杂的力学特征，广大学者都对岩石开展了大量的三轴试验研究[1−2]，合理构建反映岩石破坏全过程的岩石本构模型是研究的热点，受到人们的广泛关注。

岩石的本构主要指的是轴向应力和轴向应变的关系。早期的研究主要是基于经典断裂力学，假定岩石为连续介质，但岩石属于强烈的非线性材料，这类研究已不能满足实际需要。岩石的破坏实质上是细观裂隙逐渐发展直至贯通的过程。目前的研究主要是基于连续损伤理论，由lemaitre[3]于1985年提出的用有效应力替换常规本构关系中应力的应力应变关系。近几年来，岩石本构的研究已经取得了不错的成果，文献[4]在岩石变形力学特征的基础上，考虑到已有模型难以较好反映初始损伤和峰后变形特征，提出了考虑初始损伤的岩石几何本构模型，在这个基础上，通过对weibull 分布参数的确定，提出了修正的岩石应变软化类本构模型。文献[5]从空隙对岩石的影响入手，考虑到围压对弹性模量的影响，基于损伤理论建立了反映弹性模量随围压的变化而变化的本构模型。文献[6]针对现有的模型不能反映岩石破坏后的残余强度特征这一问题，将岩石假设为损伤和未损伤两部分，其中损伤部分承受残余强度，建立了岩石全过程的损伤本构模型。文献[7]将岩石抽象为空隙和骨架，提出空隙应变比的新概念，利用岩石三轴试验数据和损伤力学理论建立了能够较好反映岩石屈服后的非线性特征的岩石本构模型。文献[8−9]基于岩石损伤本构模型分别采用Drucker-Prager 和Mohr-Coulomb 破坏准则，使岩石微元强度服从某一种统计分布，建立了岩石统计损伤本构模型。文献[10−11]考虑岩石的应变软化和硬化特性相互转化的问题，引入损伤力学理论建立岩石本构模型。文献[12]考虑了岩石破坏时孔隙水压力的影响，引入Terzaghi 有效应力原理，构建了考虑孔隙水压力的岩石本构模型。

纵观前人对岩石的本构模型研究，有的研究了岩石裂隙压密过程的影响，建立了考虑初始损伤或者损伤阀值的岩石本构模型[13−14]，有的研究了残余强度修正值对岩石破坏的影响[15]，而同时考虑压密过程和残余强度的研究却鲜有人研究。岩石在破坏初始过程会有裂隙压密机理存在，这一阶段岩石的弹性模量E和泊松比v并不是一成不变的，在以往的研究中大都把E和v看成了恒定值，这样往往会导致最后的研究结果产生误差，不符合实际。实际上随着围压的不断增加，弹性模量E会不断增大，最后趋于稳定值，而泊松比v则会不断减小，最后趋于定值[16]，这都是由岩石本身的复杂力学性质引起的，尤其是各向异性。文章基于文献[16−17]的理论拟合，对弹性模量E和泊松比v采用随围压变化的修正值，岩石微元强度尝试采用更符合实际经验的Hoek-Brown 准则，在已有的岩石损伤力学模型的基础上，采用对数正态分布，建立了综合考虑压密过程和残余强度的岩石损伤统计本构模型。

1 岩石统计损伤本构模型

1.1 岩石损伤本构模型

目前对于损伤力学的研究方法主要分为宏观和细观损伤力学两种，细观损伤力学主要涉及岩石内部微裂隙的扩张，并逐渐发展成主裂缝的过程。宏观损伤力学则是将岩石内部随机分布的节理、裂隙考虑成初始损伤，定义损伤变量D为损伤面积与总面积之比[4]，其表达式如下：

式中，Ad为岩石损伤面积；A为岩石完整面积。

现有很多基于lemaitre 应变等价性假说建立的岩石本构模型[3]，即：

式中，D为损伤变量；为有效应力；σ为表观应力。这种模型在反应岩石残余强度特征的时候存在误差。文献[5]将作用于外力下的岩石假定为损伤和未损伤两部分，提出了能反映岩石残余强度特征的本构模型，即：

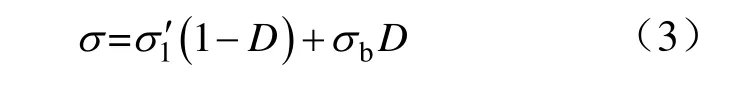
式中，σb为岩石的残余强度。该模型相对式（2）的优点明显，式（2）D为0 的时候，岩石未发生损伤，D在0 到1 之间的时候，说明岩石一开始就发生了损伤，考虑了初始损伤，D为1 的时候，发现岩石已经没有了承载力，不符合实际研究结果，式（3）既体现了岩石破坏的损伤过程，又体现了岩石的残余强度特征，更符合岩石的实际。

对于未损伤部分为线弹性材料，符合广义虎克定律，即：

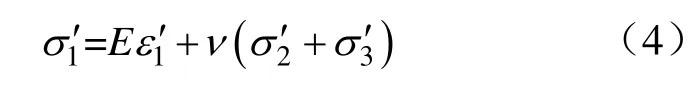
式中，E，ν分别为岩石的弹性模量和泊松比；为未损部分的细观应变。

对于岩石的破坏，假定只在轴向发生，侧向不发生，岩石表观应变与细观应变等价[8]，将式（4）代入式（3），得：

式（5）即为改进的新型岩石损伤本构模型。

1.2 岩石微元强度的确定

目前应用的强度准则大都是Mohr-Coulomb 准则和Drucker-Prager 准则，两者都能很好地度量岩石损伤，但前者不能描述高低应力区以及低应力区的强度特性，而后者结果稍偏于保守。文章尝试采用Hoek-Brown 经验强度准则来描述岩石的力学特征。H-B 强度准则相较于M-C 和D-P 准则可以考虑到岩石的结构、节理等多方面的因素。

H-B 强度准则由E.Hoek 和E.T.Brown 首次提出，能够反映岩石极限主应力间的非线性关系，表达式如下：

式中，σ1为最大主应力；σ3为最小主应力；σc为岩石单轴抗压强度；m为岩石的经验参数，反映岩石的软硬程度，取值范围为0.001～25；s为经验参数，反映岩石的破碎程度，取值范围为0～1。m和s的取值一般根据岩石的材料和分类确定。

岩石的强度常用下式来表示，即用岩石的破坏准则表示，表达式如下：

式中，K为一个随荷载变化的常数，度量岩石的峰值破坏，式f（σi）-K＞0 则表示了岩石已经超过峰值强度开始破坏，令岩石服从霍克—布朗强度准则，用F表示岩石微元强度，即：

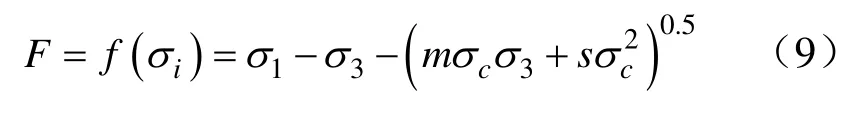
1.3 岩石统计损伤本构模型

对于统计损伤模型的建立方法，首先是合理的定义损伤变量，然后采用某种岩石破坏强度准则度量岩石微元强度，最后采用适宜的统计分布可得到演化方程。在过去已有的模型当中，采用较多的有weilbull 分布、对数正态分布、正态分布、幂函数分布等等，假定岩石微元强度服从对数正态分布，可得岩石统计损伤本构模型，即：

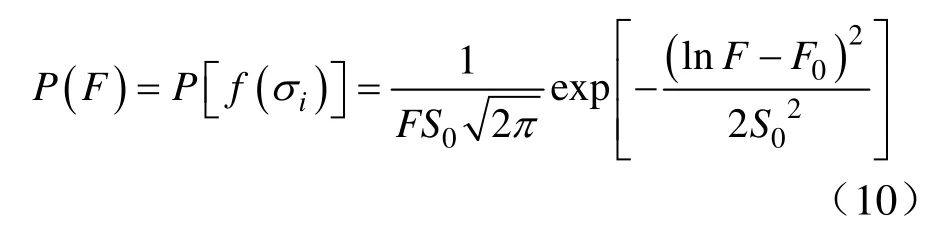
式中，F0、S0为对数正太分布参数，假定岩石微元强度符合概率密度函数，定义损伤区域D，即有：

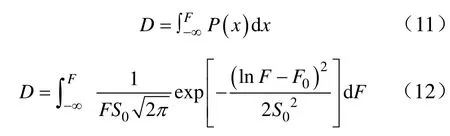
式（12）通过对比标准正太分布可得，

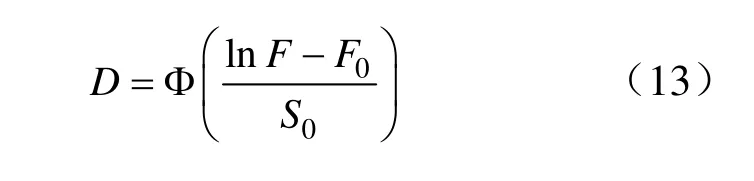
将式（9）和式（13）代入式（5）即得到新型反映初始压密过程和残余强度的岩石统计损伤本构模型。

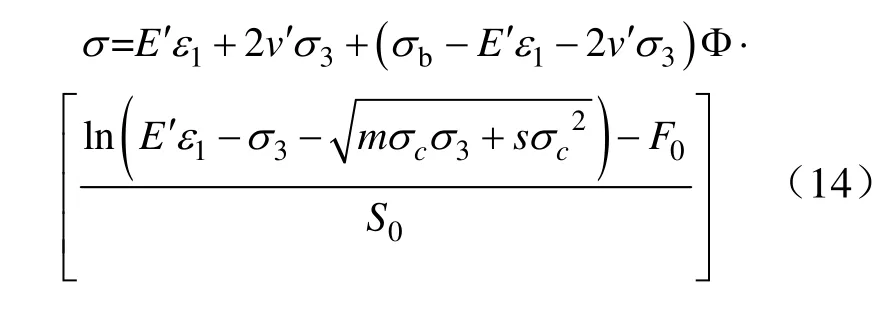
2 模型参数的确定

对于E和ν采用修正拟合随围压变化的E′和ν′[14−15]：

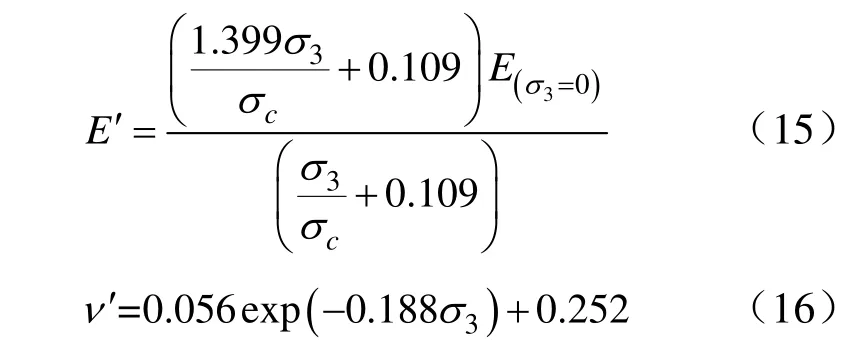
E（σ3=0）为初始弹性模量，由式（15）、式（16）可知，弹性模量和泊松比都随着围压的变化而变化，对比两者是恒定值的情况更加符合岩石破坏的实际情况。

对数正态分布参数的求解，一般是联立式（5）和式（13），利用式（5）解出D的数学表达式可得：

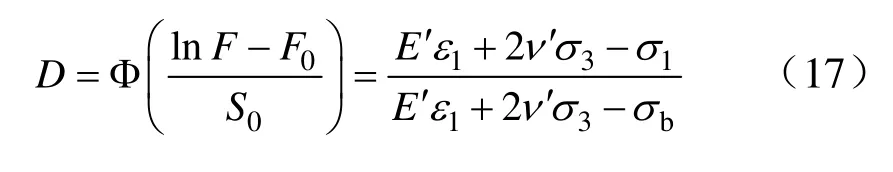
将式（17）进行变形，可得：

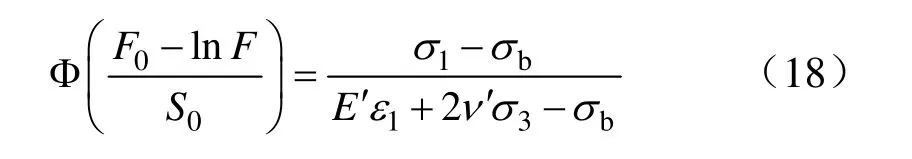
对于一组1σ、3σ、1ε、bσ的试验值，可以确立一个值，由标准的正太分布查表可得对应的值，令y=lnF，则。y值由式（9）得到，采用曲线拟合方法，多组数据求解F0和S0。

3 实例验证

为验证文章提出的岩石损伤本构模型的合理性，拟采用文献[8]的资料，岩石材料为粉砂质泥岩，岩石单轴抗压强度cσ为11.96 MPa，通过常规的试验处理数据方法得到力学参数见表1。

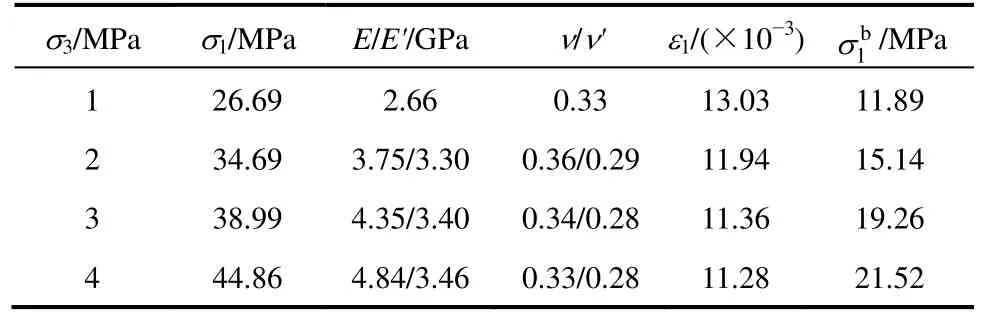
表1 粉砂质泥岩力学参数

对于E和v采用式（15）和式（16）得到修正值。通过查询标准正态分布表，同时利用多组围压数据代入式（18），即可得到参数S0和F0的值。对于H-B 强度准则中的经验参数取值，将式（7）变形得到式（19），利用多组围压数据以及参数S0和F0的值，通过解多组方程，即可求得参数m和s的值[18]。

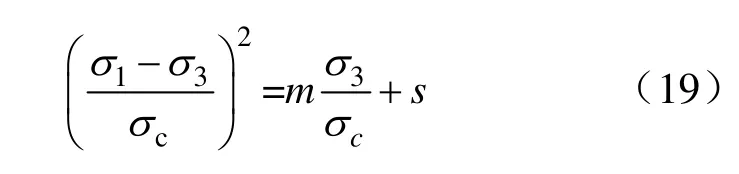
利用4 组数据和文献[8]进行曲线拟合，结果如图1 所示。

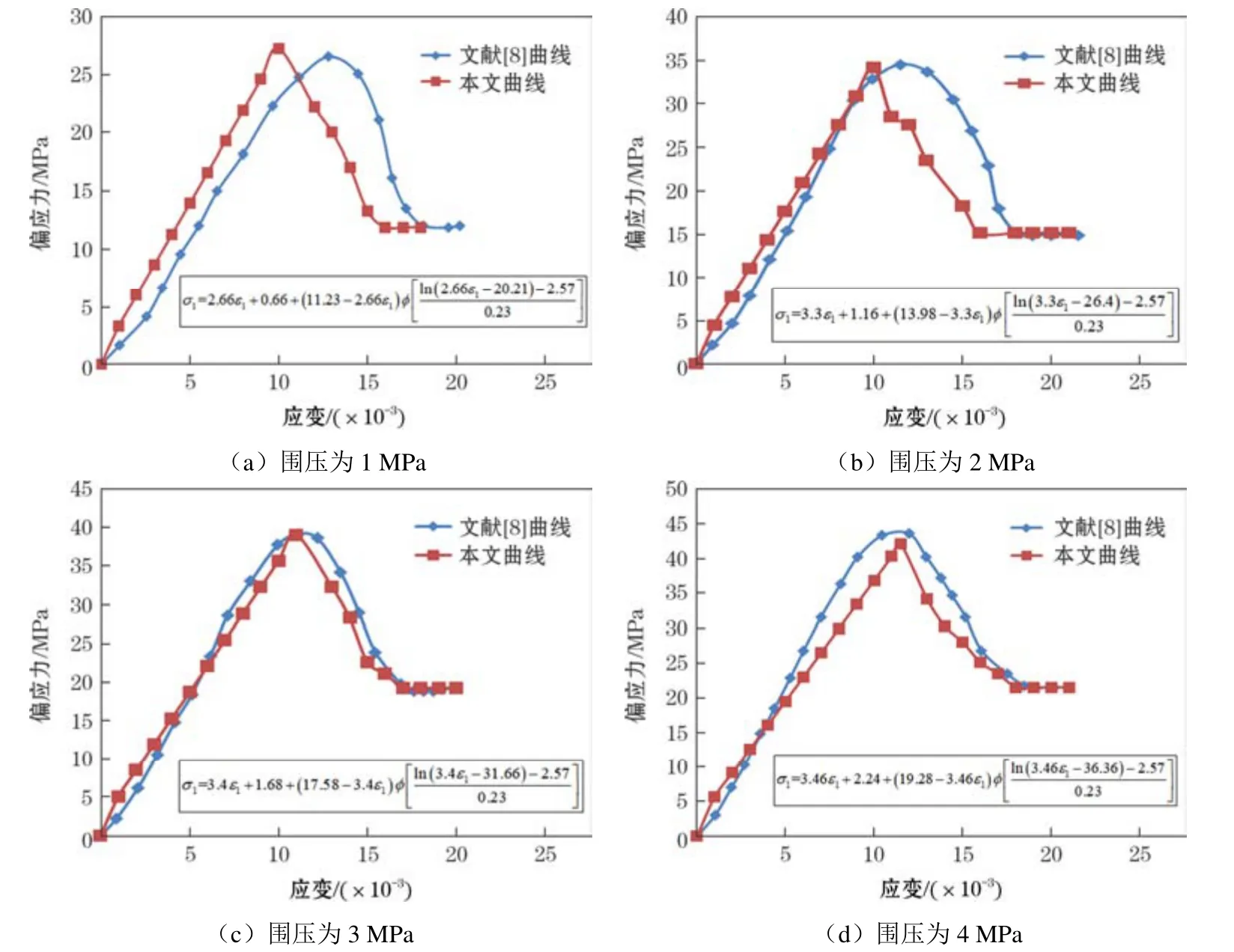
图1 不同围压下的岩石应力应变曲线

4 结果与讨论

典型的岩石全应力应变曲线主要分为5 个阶段，如图2 所示，在OA段，曲线向外凹陷，斜率逐渐增大，此时岩石内部的微裂隙逐渐压密，卸去荷载，岩石变形逐渐恢复，为弹性阶段。AB段曲线接近直线，应力应变为线弹性阶段。BC段曲线向外凸起，斜率逐渐变小，岩石开始屈服，裂纹开始快速成长，C为峰值点，岩石到达极限承载强度。CD段岩石承载能力快速下降，此时岩石内部的裂隙开始贯通，表现为应变软化，D点以后，随着应力的增加，岩石强度不再降低，表现为岩石的残余强度。

图2 岩石全应力应变曲线

文章建立的本构模型从整体上与文献[8]吻合良好，图1 和图2 也基本相符，特别是在反映岩石破坏后的残余强度方面，这说明考虑了修正后的弹性模量和泊松比的岩石本构模型能够更好地符合实际，但本文也有很多值得深究的方面。

（1）曲线拟合的对象只有一个，相对来说比较单一，这是由于资料受限以及一些其他客观因素造成的。在验算模型的时候需要的参数比较全面，因而计算过程相对合理，使得本文更有说服力。

（2）在考虑了弹性模量和泊松比的修正后所得到的模型在应变软化阶段相对没有吻合良好，究其主观因素主要是由于式（18）对于参数m和s求解的误差。对于m和s更科学的求解方法，由于没有实验条件测得相应的数值，因而采用式（18）的求解方法。

（3）采用的Hoek-Brown 强度准则，虽能够反映岩石高低应力区和拉应力区的强度特征，但是它忽略了岩石中主应力的影响，这也是需要改进的地方，希望有改进的Hoek-Brown 强度准则以便更好地模拟岩石的破坏全过程。

5 结论

在已有的岩石损伤本构模型的基础上，针对已有模型未能考虑弹性模量和泊松比随围压变化而变化的情况，基于霍克-布朗强度准则，采用对数正态分布所建立的岩石损伤统计本构模型，可以得到如下结论：

（1）从曲线拟合情况来看，能够很好地反映峰前的变形特征和岩石的残余强度，同时也能够反映岩石破坏的全过程。本文旨在为同类研究提供一个新的方向，即根据弹性模量和泊松比随围压的变化情况来建立岩石的本构模型。

（2）统计损伤本构模型采用的是Hoek-Brown强度准则，相较于M-C 和D-P 准则来说，考虑了岩石的结构、节理等因素，且能够反映岩石高低应力区及拉应力区的强度特征，有一定的优势。

（3）建立的模型考虑了随围压变化而变化的弹性模量和泊松比，相比于采用定值的弹性模量和泊松比，更加符合岩石加载破坏的实际情况，因而本模型有更好的适用性，且参数较少，求解简便，在同类研究中，可以提供很好的参考。