联合势场与蚁群算法的机器人路径规划*
赵 娜,陈越峰,2
(1.辽东学院机械电子工程学院,辽宁 丹东 118000;2.华北理工大学矿业工程学院,河北 唐山 063210)
0 引言
路径规划是机器人控制领域的重要研究方向[1],主要用于为移动机器人在障碍环境中规划一条至目标点的最优路径。目前,这一方面的诸多研究已取得显著成果,如遗传算法、A*算法[2]、人工势场算法[3]以及蚁群算法等。
蚁群算法通过正反馈智能机制,具有并行、分布式计算、强鲁棒性及快速收敛等特点,更适于移动机器人在障碍物环境下的路径规划问题,但传统蚁群算法初始路径搜索效率低,易停滞和陷入局部最优,为此,学者提出大量改进算法:许凯波等[4]提出双层路径搜索的改进蚁群算法,通过内外双层路径寻优提高路径质量,并设计了信息素二次更新策略;封声飞等[5]通过改进启发信息和信息素更新策略,平衡算法的收敛速度和寻优能力,并采用分段贝塞尔曲线进一步平滑;Zheng 等[6]采用多策略进化机制,通过信息素进行随机初始化和交叉操作,提高算法搜索能力,通过选择概率自适应调整提高算法的随机性;白建龙等[7]设计了负反馈蚁群算法,利用历史搜索信息积累失败经验,以指导蚁群对未知空间的搜索,以解决蚁群算法后期的多样性问题;Ma 等[8]采用双参数控制改进蚁群算法的计算效率,并建议了路径规划模型,但优化效果不明显;Tiffany 等[9]利用头尾搜索机制改善蚁群前期收敛,通过奖惩因子与信息素阈值提高全局搜索能力,引入遗传算法避免局部最优。
人工势场算法结构简单,计算量小,但在复杂障碍物环境易产生死锁或局部最优,为此,近年来,综合势场和蚁群两种算法各自优点的混合算法开始应用于机器人路径规划,罗德林等[10]以势场虚拟合力和目标距离优化蚁群算法的启发信息,在联合人工势场优化基础上,避免算法陷入停滞;刘建华等[11]采用人工势场与蚁群信息素融合,构建局部扩散信息素,使蚁群在路径搜索时更倾向于搜索高适应值子空间,从而提高收敛速度和寻优能力;Liu等[12]以改进的人工势场算法获取局部路径,并用于蚁群的信息素初始化,使其初始搜索具有方向性;任彦等[13]采用虚拟牵引力和快速函数对人工势场进行改进,并将改进的势场合力作为路径搜索启发信息的一部分,改善了蚁群算法的全局搜索能力;王晓燕等[14]将人工势场初始路径和递减系数引入启发信息,并对初始信息素采用不均衡分配策略,提高算法的搜索效率,避免了停滞问题。
相比于经典蚁群步进,人工势场与集群算法联合较好地提高算法的全局寻优和收敛性,但已有的人工势场与集群算法联合仍存在易陷入局部最优、前期路径有效性差等问题,为此,在已有研究基础上,提出了基于改进人工势场局部搜索和改进蚁群算法全局搜索的机器人路径规划算法。利用有效障碍物检测和临时中间目标点改进人工势场算法,并通过改进人工势场优化蚁群算法的初始路径搜索,同时构建与收敛相关的负反馈通道,调节全局与局部信息素的自适应更新,以平衡算法的收敛速度与全局搜索能力。仿真结果验证了该算法的有效性。
1 改进人工势场局部路径规划
人工势场算法在运行环境中施加目标点引力与障碍物斥力两种虚拟力场,由引力与斥力的共同作用获得机器人的最优路径规划与有效避障。但传统算法存在引力斥力相等且方向相反时的死锁现象、目标点不可达、多障碍物计算效率问题,以及斥力影响导致的非最优路径等问题,为此,提出改进的人工势场算法。算法首先根据直线路径检测有效障碍物并设置中间目标点,然后根据最终目标点引力与有效障碍物边缘斥力共同作用,完成中间目标点的局部路径规划,直到中间点迭代到最终目标点。
1.1 运动环境栅格化
根据棋盘思想,将空间离散化成栅格是运动环境建模的常用方法[5],其根据栅格是否可通过而将空间划分为自由栅格和障碍物栅格,并通过局部栅格的腐蚀或膨胀进行细化描述[7]。
设机器人运动环境所在的矩形平面内,机器人运动起点和目标点坐标为(0,0)和(l,h),即矩形平面区域为l×h,取栅格尺寸为a×a,则区域长和宽两个方向上的栅格数为(Nh,Nl)=(cel(h/a),cel(l/a)),则每个栅格的行列编号相应地生成栅格的坐标。如图1 所示为测试文中算法适用性建立的仿真环境,图中机器人起点与目标点分别设置在平面区域的左下角和右上角。

图1 算法分析采用的仿真环境
有效障碍物直接影响机器人的最优路径规划,文中在路径规划时,先对其进行识别并设置中间目标点,基本思想为:首先以机器人运动场景内的起点到最终目标点之间的直线为参考,当障碍物位于该参考直线上时,为有效障碍物,然后计算障碍物栅格边沿到参考直线的距离极值,并以极值点作为当前迭代的中间目标点[9]。
1.2 改进人工势场
设机器人在栅格地图中运动时采用8 邻域行进[8],即机器人每次移动至其8 邻域的一个栅格,则机器人在当前栅格中将受到如图2 所示的某个方向的力作用,采用3×3 阶的作用力矩阵来存储各方向作用力及力的作用方向,如图2 所示。

图2 作用力矩阵的力方向示意
由于斥力的存在,传统人工势场无法使机器人紧贴障碍物运动[8]。为此,在机器人靠近有效障碍物移动时,引入边界约束以替代斥力作用,这样,机器人受力只与终点引力及其外部环境相关,设机器人在位置X 处的作用力矩阵为

式中,*为卷积运算,Fijg为终点引力的最优分解矩阵,Eij为机器人外部环境的3×3 阶约束矩阵,用于描述机器人的8 邻域状态,Fijg描述了最终目标点引力在当前栅格的8 邻域分解情况,其各元素为:
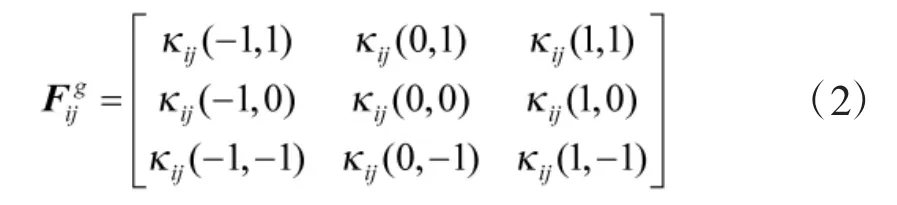
式(2)中,Fijg各元素需满足式(3)以确保最优分解,即
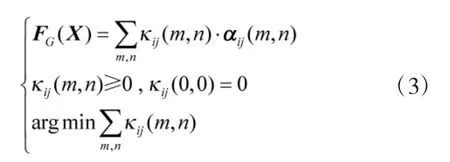
式中,m 和n 为矩阵FG(X)的行列号,m,n∈{-1,0,1},αij=(m,n)为当前栅格下机器人可移动方向,κij为Fijg在αij方向上的投影系数。机器人总是移向局部受力最大的方向,则基于临时中间目标点的局部路径规划的计算式为:

步骤1:对相关参数初始化,包括起点Xs、最终目标点Xd、临时中间点Xl,ω等位置参数,引力增益系数kd及栅格地图信息相关的临时矩阵Zx、搜索矩阵Zs和作用力矩阵。
步骤2:搜索检测有效障碍物并根据其设置临时中间目标点,将该中间目标点设为局部路径规划的终点。
步骤3:重复步骤2 进一步搜索有效障碍物及中间目标点,直到搜索不到新的有效障碍物,此时,将最后障碍物的栅格信息复制到Zs中。
步骤4:根据Zs中障碍物栅格信息,采用文中改进人工势场更新作用力矩阵,然后由最大受力方向从起始开始机器人的路径搜索,得到一个局部路径。
步骤5:将局部路径的终点设置为新起点,重复步骤2 和步骤3,搜索新的有效障碍物和局部终点,并根据步骤4 进行局部路径规划,直至最终目标点变为局部目标点,则迭代搜索完成,各局部最优路径组成机器人全局路径。
改进算法通过中间目标点优化各局部路径的规划,由于经过有效障碍物搜索,中间目标点内无新障碍物和中间点存在,因而有效避免经典算法的死锁现象。同时,由于不考虑接近时斥力,机器人可紧贴近障碍物移动,使得局部路径更优。
2 改进蚁群全局规划算法
2.1 经典蚁群算法
蚁群算法[9]通过蚂蚁群体与环境之间的信息交互来实现最优路径搜索,其主要包括概率选择和信息素更新两个关键步骤,概率选择指蚂蚁在路口时按一定概率选择下一节点,通常采用伪随机比例原则[10],其路径选择概率为:

式中,ak为可选择的下一节点集合,与为节点转移的信息素浓度,与为节点间启发信息,α 与β 为信息素的启发因子及其期望值,信息素更新指根据节点上已有信息素引导后续蚂蚁选择最优路径。经典蚁群算法兼顾全局和局部的信息素更新,其全局与局部更新式分别为

根据式(6)和式(7)可知,全局更新加强最优路径中节点信息素以加速算法收敛,而局部更新则削弱节点信息素,以减少重复访问概率,增强全局搜索能力。
2.2 启发信息的改进
为考虑节点间障碍物对欧氏距离djg的影响,借助人工势场快速的计算特点,文中以改进人工势场得到节点j 到临时中间目标点g 之间的距离rjg替代djg,同时为提高距离计算准确性,引入当前节点i 与待选节点j 间的距离dij,在算法迭代后期,为提高全局搜索能力,引入诱导因子ξ∈(0,1]以削弱迭代后期启发信息的作用,这样,改进启发信息公式为:

2.3 信息素更新方法的改进
信息素更新对算法的不同阶段性能起重要作用,但由于算法各阶段性能要求不同,传统的固定更新策略不利于算法的性能达到最优,为此,提出一种信息素自适应更新策略,其全局和局部更新计算式为:
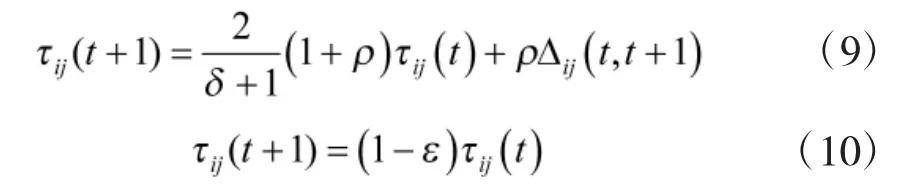
2.4 改进蚁群算法流程
根据对蚁群算法启发信息与信息素调整策略的改进,文中改进蚁群全局路径规划的算法流程如图3 所示。

图3 改进蚁群算法流程图
步骤1:算法参数初始化:起始与目标点位置:Xs、Xd,计数器:Ns、NC和NCmax,蚁群规模N,启发与及诱导因子,α、β、ξ,信息素矩阵及全局与局部挥发系数:T、ρ 和ε;
步骤2:迭代蚁群路径:将Xs放入禁忌表,计算rjg并代入式(8)以计算ηij,然后根据式(10)确定蚂蚁的下一节点,并将其放入禁忌表中,循环计算rjg、ηij,直至到达最终目标点Xd;
步骤3:全局及局部信息素的更新:由式(9)局部更新蚂蚁建立的每一条路径的信息素,当蚁群所有蚂蚁完成一次迭代路径规划后,按式(10)对当次迭代后的最优路径进行全局信息素的更新;
步骤4:如果NC 为验证文中所提算法的最优路径规划有效性,以图1 所示的简单和复杂障碍物栅格环境为机器路径规划仿真环境,实验软件为Matlab R2010a,计算 机 环 境 为:Windows10,Core i7-8700K 3.7 GHz CPU,16 G 内存,采用已有文献中的基于负反馈机制的蚁群算法(简记为Nfa-RPP 算法)[7],及文献中的基于零点理论与人工势场改进的自适应蚁群路径规划算法(简记为ZaA-RPP 算法)[14]作为实验比较算法,根据文献研究及多次实验结果平均值,算法主要参数设置为α=2,β=6,ξ=0.2,ρ=0.7,ε=0.5,其他参数根据实验栅格进行设置,如表1 所示。 表1 实验涉及的相关参数设置 3 种算法在图1 所示复杂环境中的路径规划仿真实验结果如图4 和图5 所示,图4 为3 种算法最优路径规划结果,图5 为3 种算法的收敛曲线。 图4 简单实验环境实验结果 由图4 和图5 可以看出,复杂栅格环境中,Dac-RPP 算法的最优路径仍陷入局部最优,其在图7 中的算法收敛速度最慢,且收敛路径最优;而文中算法与ZaA-RPP 算法都避免了局部最优结果的出现,取得相等的最优路径长度;但从图7 收敛曲线可以看出,由于ZaA-RPP 算法中信息素在全局与局部路径规划中交替产生作用,其收敛曲线会随之产生影响收敛速度的曲线波动,从而文中算法通过构建迭代相关的信息素负反馈通道,有效缓解迭代波动,从而提高收敛速度,如表2 所示。在取得相同的最优路径长度下,文中算法只需要较少的迭代次数可得最优解。 图5 各算法的收敛结果 表2 实验比较结果 为进一步分解算法的全局搜索能力,将复杂格栅环境下3 种算法实验过程中蚁群的自有搜索路径,其结果如下页图6 所示,采用环境覆盖率φ 量化分析算法全局能力,其计算式为: 式中,Npass与Nfree为复杂环境中搜索栅格数与所有非障碍物栅格数。 由图6 实验结果可见,文中算法与ZaA-RPP算法取得更广泛的全局搜索范围,因而其搜索到最优路径的可能性更大。根据式(11) 计算的ES-PSO 算法、ZaA-RPP 算法和文中算法,3 种算法的环境覆盖率分别为55.38 %、70.95 %和71.19 %,可见,文中提出的改进算法取得最大覆盖率,其最优路径的搜索概率也越大,因而具有较好的全局搜索能力[15-17]。 图6 复杂实验环境路径搜索结果 针对全局静态环境下传统蚁群算法应用于机器人路径规划时,易陷入局部最优、前期路径有效性差等问题,对传统蚁群算法进行改进,提出了基于改进人工势场局部搜索和改进蚁群算法全局搜索的机器人路径规划算法。算法在地图环境栅格化基础上,首先利用有效障碍物识别和临时中间目标点改进人工势场,优化其死锁和欠优问题,其次,通过改进人工势场优化蚁群算法的初始路径搜索,避免其早期的交叉等问题,同时构建与收敛相关的负反馈通道,自适应调节全局与局部信息素更新,以平衡算法的收敛速度与全局搜索能力。简单环境与复杂环境的仿真实验结果表明,所提算法有效避免局部最优,具有较好的全局搜索能力,收敛速度和搜索能力优于实验采用的已有改进蚁群算法,验证了该算法的有效性。 但文中启发信息改进公式主要基于实验结果以及简单的理论分析,深入的理论分析和最优结果论证将在后续工作中进一步展开研究。3 仿真实验验证及分析

3.1 复杂环境实验比较





4 结论

