多因素观测来源不确定的多目标跟踪算法*

王 颖

（商丘职业技术学院机电系，河南 商丘 476000）

0 引言

传统多目标滤波器在跟踪前需要建立目标与观量的关联［1-3］，因此，该类滤波器难以应用于目标数目时变的目标跟踪场景，且计算复杂度随虚警增多呈指数增长。基于有限集统计学［4］的概率假设密度（PHD）［5］滤波器绕过了复杂的数据关联，因此，受到了目标跟踪领域越来越多学者的关注［6-9］。线性高斯噪声动态系统下，高斯混合PHD（GMPHD）给出了PHD 滤波器的一种闭合解［10］。

GMPHD 滤波器具有目标状态提取简便和计算复杂度低等优点，被广泛应用于目标跟踪领域［11-13］。针对杂波环境下杂波和目标观测来源不确定的目标检测和跟踪问题，Baisa 等［14］提出一种基于GMPHD 的多目标多类型滤波（MTMTF）算法。该算法采用目标分类更新策略，克服了GMPHD 滤波器更新步中不同类型目标观测的相互干扰。然而，MTMTF算法只能处理杂波与目标观测的归属不确定性问题，无法解决近邻目标观测来源不确定的问题。标准Bayes 滤波框架下，Aoki 等［15］从理论上分析了杂波环境下，源于近邻目标的观测不确定性和观测-目标间关联等问题。然而，文献［15］仅仅从理论上给出了近邻目标观测不确定性的分析与证明，没有给出具体的实现。针对由不精确检测导致的观测来源不确定问题，Yazdian-Dehkordi 等［16］提出一种多扫描惩罚GMPHD（NSP-GMPHD）滤波器。借助于目标前N 个时刻的状态估计，NSP-GMPHD 滤波器从当前时刻后验强度中估计不同目标的状态。密集杂波跟踪场中，多扫描推测技术的引入使得NSP-GMPHD 滤波器的计算效率很低。基于权重指数衰减函数和多帧技术，Zhang 等［17］提出一种状态精度和计算效率均衡的GM-PHD（IUMF-GMPHD）滤波器。通过利用前一时刻目标的权值，权重指数衰减函数，可以有效地解决由近邻目标观测不确定性导致的目标权值失衡问题，以及杂波与目标量测观测来源不确定问题。然而，多帧技术的引入同样使得IUMF-GMPHD 滤波器的计算代价较高。此外，含有多类型观测来源不确定的密集杂波多目标跟踪环境下，IUMF-GMPHD 滤波器的状态估计精度仍相对较低。

通过改进GMPHD 滤波器，提出一种多因素观测来源不确定的多目标跟踪算法。通过引入标记和权重向量作为目标的辅助参量，结合高斯分量合并策略、目标状态估计策略和高斯分量优化策略，本文算法能够提高多因素观测来源不确定跟踪环境下目标状态估计精度和滤波迭代效率。

1 基于随机有限集的GMPHD 滤波器

预测步：假设k-1 时刻后验强度由高斯混合表示为

其中，ps，k为存活概率，第i 个高斯分量的预测均值和预测协方差分别为

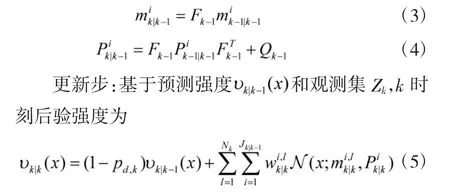
其中，等式右侧第1 项为漏检项后验强度，第2 项为观测更新项后验强度。

2 观测来源不确定的GMPHD 算法

目标观测来源不确定主要由3 种因素所导致。1）杂波因素。未知目标-观测关联条件下，滤波器通常难以有效地区分杂波和源于目标的观测。2）低检测概率因素。低检测概率的目标跟踪环境下，源于目标的观测可能难以被传感器探测到。3）多目标相互近邻因素。当目标相互近邻时，滤波器难以区分源于不同目标的观测，将导致目标状态更新错误和目标分量错误合并。

2.1 高斯分量合并策略

2.2 目标状态估计策略

当传感器的检测概率较低时，场景中所有真实目标难以被传感器全部探测。采用不完整观测集更新预测强度后所得到的后验强度的精度相对更低，因此，部分目标状态难以从低精度后验强度中估计。为了从低精度后验强度中正确地估计目标状态，提出一种新的目标状态估计策略。

2.3 高斯分量优化策略

3 实验结果与分析

采用本文算法分别对NSP-GMPHD［16］和IUMFGMPHD［17］滤波器进行改进，得到Novel-NSPGMPHD 和Novel-IUMF-GMPHD 滤波器。基于OSPA 距离［18］和运算时间，将改进后的滤波器与原始滤波器进行性能对比，其中，OSPA 距离的两个参数分别为p=1 和c=200。实验结果为200 次Monte-Carlo 仿真实验的平均值。目标存活概率ps，k=0.99，分量数目截取阈值=4，存活比率阈值μs=0.4，新生比率阈值μn=0.6，元素数目阈值ρTH=5，状态抽取阈值=0.5。状态噪声服从零均值、标准差为0.5的高斯分布，观测噪声服从零均值、标准差为49 的高斯分布。

实验1：杂波和近邻目标因素引起的观测来源不确定

实验场景为一个［-700 m，700 m］×［-700 m，700 m］二维监视区域，其中该区域中含有3 个相互交叉的目标。图1 给出了实验场景的100 s 仿真示意，其中杂波数目服从均值为10 的均匀分布和检测概率pd，k=0.95。

图1 目标轨迹和观测

图2 给出了100 次Monte-Carlo 实验的OSPA距离和运算时间的结果对比。Novel-NSP-GMPHD和Novel-IUMF-GMPHD 滤波器具有较小的OSPA距离的原因为：高斯分量合并策略的应用，极大地避免了基于近邻目标观测相互干扰的观测来源不确定所导致的高斯分量合并错误；目标状态估计策略的引入，较好地改善了由低检测概率引起的观测来源不确定所导致的目标状态漏估计。由于高斯分量优化策略能够有效地降低滤波迭代中后验强度内无效分量的比重，因此，Novel-NSP-GMPHD和Novel-IUMF-GMPHD 滤波器的迭代效率均高于NSP-GMPHD 和IUMF-GMPHD 滤波器的迭代效率。良好的滤波性能表明，本文算法能够有效地解决多因素观测来源不确定下的多目标跟踪问题。

图2 各滤波器100 次Monte-Carlo 结果对比

实验2：不同检测概率环境下的多因素观测来源不确定

图3 为检测概率对各滤波器性能影响的结果对比，其中杂波数目服从均值为8 的均匀分布且其他场景参数与实验1 相同。相较于NSP-GMPHD 和IUMF-GMPHD 滤 波 器，Novel-NSP-GMPHD 和Novel-IUMF-GMPHD 滤波器，在各个检测概率处均具有较小的OSPA 距离和较少的运算时间。得益于高斯分量优化策略能较好地控制分量数目，两个改进滤波器的运算时间几乎不随检测概率的变化而变化。该组实验结果表明：在高斯分量合并和优化策略的协助下，目标状态估计策略，能够改善由低检测概率引起的观测来源不确定所导致的目标漏估计及计算效率问题。

图3 检测概率对各滤波器性能影响对比

实验3：不同杂波数目环境下的多因素观测来源不确定

图4 给出了各滤波器在不同杂波均值场景下的结果对比，其中检测概率pd，k=0.93 且其他场景参数与实验1 相同。 相较于NSP-GMPHD 和IUMF-GMPHD 滤 波 器，Novel-NSP-GMPHD 和Novel-IUMF-GMPHD 滤波器总体上具有较小的OSPA 距离和较少的运算时间。该组实验结果表明：基于目标状态估计策略和高斯分量优化策略的辅助，高斯分量合并策略，能够提高由杂波和近邻目标所导致的观测来源不确定下的目标状态估计精度和计算效率。

图4 杂波数目对各滤波器性能影响对比

实验4：分量数目截取阈值对滤波算法性能的影响

图5 分量数目截取阈值对本文算法的影响

4 结论

本文提出一种针对多因素观测来源不确定的多目标GMPHD 滤波器。通过迭代地传递目标标记、目标权重向量和目标后验强度，高斯分量合并策略，能够有效地避免由杂波和近邻目标引起的观测来源不确定所导致的高斯分量合并错误，目标状态估计策略，改善了由低检测概率引起的观测来源不确定所导致的目标漏估计，高斯分量优化策略通过减少后验强度中无效的高斯分量，以降低滤波器的计算代价。实验结果表明，本文算法能够有效地改善多因素观测来源不确定环境下的目标状态估计精度和滤波迭代效率。