无人机对地攻击时敏目标威胁度SPA-IELM 评估方法

王 倩，甘旭升，于海龙，韩宝安

（1.西京学院理学院，西安 7101231；2.空军工程大学空管领航学院，西安 710051；3.解放军93523 部队管制室，山西 永济 044500；4.四川交通职业技术学院信息工程系，成都 611130）

0 引言

无人机作为一种新兴装备，凭借续航时间长、机动性强、成本低廉等特点，已逐渐在战争中扮演越来越重要的角色。在无人机对地攻击多个时敏目标时，能够根据战场态势信息，精确预判，科学决策，将火力资源合理配置在地面目标上，对顺利、高效完成作战任务至关重要［1］。而时敏目标威胁度是影响决策过程的关键要素［2］，可根据地面时敏目标威胁度评估值合理分配无人机的火力资源。随着地面时敏目标的机动能力与防御能力增强，如何根据实时变化的战场态势，对地面时敏目标威胁度进行自动、快速和准确的评估，为无人机攻击地面目标提供决策支持，已成为当前的研究热点之一。

杨州等利用改进层次分析法来解决对地攻击方案的优选问题［3］，并在攻击方式决策中考虑了目标性质和火力威胁，但对目标威胁缺少系统性研究。鲁华等采用灰色关联分析法对目标威胁度进行研究，提出了一种目标威胁度计算方法［4］，但该方法评估中需要现行确定各项指标的最优值，主观性过强，且部分指标最优值难以确定。曲长文等基于矩阵对策原理构建了目标威胁评估模型［5］，通过敌我双方策略对比并求解威胁矩阵来进行目标威胁评估，然而该方法建立策略集需要依靠先验知识，主观因素影响较大。王永杰等基于TOPSIS 方法对空战中目标的威胁度评估问题进行了研究［6］，该方法充分利用目标因素的不确定性信息，便于工程实践，其缺点是对数据比较敏感。符永军等将模糊优选理论与层次分析法有机结合，为某型地空导弹系统建立了威胁度评估模型［7］，但由于专家主观标度上的差异，使评估的可信度受到了影响。综上可知，这些研究在构建评估模型的某个环节中，如数据采集、体系建构、指标赋权以及模型构建，不同程度上依赖于专家的先验知识，导致评估结果不可避免地带有主观性。此外，这些研究都没有考虑实战中非常重要的问题，即评估的时效性问题，离开时效性谈目标威胁度评估，对攻击决策就失去了实际意义。

基于此，提出了基于集对分析（Set Pair Analysis，SPA）与增量型极限学习机（Incremental Extreme Learning Machine，IELM）的无人机对地时敏目标威胁度评估方法，即通过SPA 处理评估过程中的主观不确定性问题，并在此基础上采用IELM 对目标威胁度进行实时评估，以辅助无人机火控系统进行科学决策。

1 集对分析法

集对分析法SPA 是赵克勤于1989 年提出了一种不确定性理论［8］。核心在通过对系统内不确定性与确定性予以分析与处理，对系统中具有关联性的集合中的同一性、差异性、对立性等特性进行分析，对系统不确定性进行描述的方法。

SPA 可描述为：定义集对Θ=（A，B），A、B 为相关联的数据集。对集对Θ 特性进行分析，得到N 个特性，S 个特性为A 与B 共有，即为“同”；P 个特性为A 与B 互斥，即为“反”；F=N-P-S 个特性对A 与B 既不共有也不互斥，即为“异”。将a=S/N、b=F/N、c=P/N 分别称为同一度、差异度与对立度。若忽略权重影响，联系度可表示为

式中，a+b+c=1；i 为差异度系数，取值区间为i∈［1，-1］，当i 有实际含义时，i=1，b 转化为a；i=-1，b 转化为c；i∈（1，-1），a 与c 各占一定比例；j 为对立度系数，其值为-1。

2 增量型极限学习机

ELM 最早由Huang 等提出［9］。训练过程中仅需调整隐层节点数，便可获取模型参数进行训练，与BP 网络、支持向量机（SVM）传统方法相比，学习效率上得到了极大改善，并在各领域得到广泛应用。然而，传统ELM 通常都采用批量训练算法，当新训练数据加入时，需要对数据重新整理进行训练，既浪费内存，又消耗时间，为解决此问题，Huang 等人在增量学习框架下提出了增量型极限学习机（IELM）［10］。这种新型的训练模型通过不断添加隐层神经元节点，并随机确定新增隐层节点的权值，可以将系统误差降低到一定程度。

假设给定的训练集样本记为（Xp，Yp），其中特征向量Xp=［xp1，xp2，…，xpn］T∈Rn，期望输出Yp∈R，且样本标记p=1，2，…，N，共有N 个训练样本。

隐神经元为L 个，隐层激活函数h（x）的ELM的输出满足

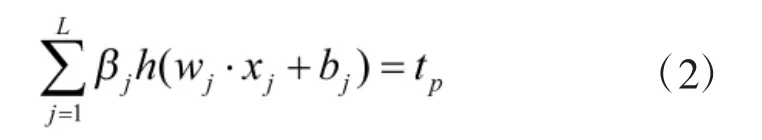
其中，wj∈Rn；bj，βj∈R。wj为输入层与第j 个隐层单元连接的权值；bj为第j 个隐层单元的偏置；βj为连接第j 个隐层单元与输出层的权值；tp为第p 个样本的实际输出。式（2）可转化为矩阵形式Hβ=T。在增量学习模型下进行数据训练，新增隐层单元连接的输出权值为

其中，e=Y－T 表示训练模实际输出T 与期望输出Y之间的差值，用来表示误差大小。

样本训练时，IELM 算法首先根据传统极限学习机原理获取L-1 个神经元对应的隐单元权值和输出层权值，然后通过随机选取新增的第L 个隐层节点的权值，继续进行训练。文献［9］证明，网络的训练误差和测试误差均会随着隐层节点数目的增多而相应减小。文献［10］指出，IELM 与增量型SVM（ISVM）具有相近的泛化性能，并且速度远快于ISVM。

3 地面时敏目标威胁度评估模型

3.1 评估实现流程

无人机在对地面目标攻击时，地面目标的类型大致分为：静止目标、运动目标和时敏目标。其中，时敏目标是时间敏感目标的简称，通常指战场上随机出现、打击机会受时间窗口严格限制且具有重要军事价值的目标。相对于静止和运动类型目标，时敏目标通常具有隐蔽性好、机动性强、状态变化频繁、出现地点不定、暴露时间短暂、对其打击机会稍纵即逝等特点。因此，对时敏目标进行攻击时，存在定位难、跟踪难、可攻击时间短等诸多困难。机动防空导弹系统、间歇开机雷达站、有人/无人驾驶军用车辆，以及敌人撤退所经过的桥梁等均属于时敏目标。因此，研究地面时敏目标威胁度的评估问题，对于提高无人机攻击决策效率，有效地杀伤敌方地面目标，改善我方无人机生存能力，充分地发挥无人机的作战效能具有重要意义。

在构建无人机对地攻击模型过程中，由于战场态势的不确定性、多变性和复杂性，导致对地面时敏目标威胁度的评估，有别于其他地面目标威胁度评估。主要体现在两个方面：一方面，存在一定的不确定性。地面时敏目标的威胁度受到相对方位、与目标的距离、目标武器威力和时敏性等诸多因素的影响，而在这些因素中，有些信息已知，有些是未知的，使得传统方法难以胜任地面时敏目标的威胁度评估；另一方面，对时效性提出更高要求。考虑到未来战争信息量大，战场环境的可变性，战斗过程应该是一个不断变化的过程，地面时敏目标的威胁度也是不断变化的，因此，评估时敏目标威胁度的评估方法必须要具有时效性、有效性及前瞻性。

针对以上两个方面的问题，结合无人机对地攻击的实战性要求，提出了基于SPA-IELM 的无人机对地时敏目标威胁度评估方法。该方法的建模评估包括两个过程：第1 个过程，根据已知信息和专家知识，利用SPA 在处理不确定性问题中的优势，进行地面时敏目标的威胁度评估，从而为后续研究构造样本数据；第2 个过程，基于获取的样本数据在线训练地面时敏目标威胁度IELM 评估模型，并完成测试验证。不难看出，采用现有SPA 处理威胁度评估中可以主观不确定性问题，但无法解决评估的时效性问题，即无法实现对地面时敏目标威胁度的自动、快速评估，进而影响了攻击决策过程；而利用文献［9］提出的IELM 进行在线训练评估，时效性很强，但获取样本数据存在困难。而本文将两者有机结合，取长补短，优势互补，既能解决时敏目标威胁度评估中存在的不确定性问题，又可实现自动实时评估，这也正是本文研究的核心思想和创新之处。无人机对地攻击时敏目标威胁度评估流程如图1 所示。

图1 地面时敏目标威胁度评估流程

3.2 评估指标选取

无人机实施对地时敏目标攻击任务时，其打击体系基本由传感器、无人机（火力打击）和指挥决策构成，如图2 所示。传感器系统通过侦察与识别作战环境时敏目标，获取态势信息；指挥决策系统通过对传感器系统获取信息进行分析、评估与决策，与其他系统进行信息沟通，保证系统顺畅运行；无人机系统作为系统决策的执行部门，通过机载火力系统打击地面时敏目标。

图2 无人机对地时敏目标打击体系组成

当传感器系统探测到时敏目标在无人机攻击范围内时，将获取的态势信息传输到指挥决策系统，决策系统通过对信息进行处理，进行时敏目标威胁度评估，最后由无人机系统对目标进行火力打击。

假设时敏目标的运动状态为匀速直线，初始位置与速度信息分别记录为X0和V0，无人机可攻击区域对应的时间窗口长度分别为［t1，t2］，则有

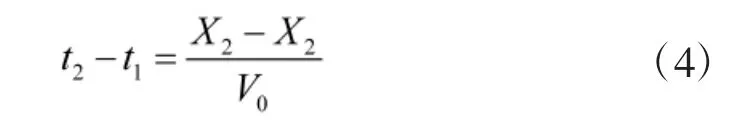
当无人机攻击区域信息固定时，时间窗口长度由地面目标的机动信息（如速度）决定，从发现到摧毁目标的时间长度也受到影响，杀伤攻击必须在t1至t2之间的时间约束下完成。因此，无人机系统对地面时敏目标攻击决策速度越快，从发现到摧毁所需时间就越短，完成任务的概率就越高。

由此可知，解决无人机对地面时敏目标的快速攻击决策问题是能否成功摧毁目标的关键，其具体可转化为对地面时敏目标威胁程度的评估和排序问题。则针对评估需求，根据文献［11］给出地面时敏目标威胁度评估指标，如表1 所示。

表1 地面时敏目标威胁度评估指标

3.3 SPA 样本构造

采用SPA 构造样本数据，需要先根据无人机对地攻击特点以及地面时敏目标威胁度评估指标，将目标威胁程度划分5 个等级：特别严重（I）、严重（II）、重大（III）、一般（IV）、轻微（V）等5 个威胁等级。同时，各项评估指标也相应划分为5 个等级。为与这5 个等级对应起来，式（1）需要拓展为

式中，a、b、c 分别为同一度、正差异度与负差异度，d与e 为对立度。（a，b，c，d，e）称为同异反向量，a，b，c，d，e∈［0，1］；i1∈［0，1］；i2∈［-1，0］，通常可按照均分原则取值［11］；j1=j2=-1。

将地面时敏目标威胁度评估指标体系中的某指标及其对应的分级标准分别列为两个集合，并构成一个集对。若指标值处于此评估级别中，则视为同一；若指标值处于相邻评估级别中，则视为相异；若指标值处于相隔评估级别中，则视为对立。为量化联系度，确定不同的联系度，对于越大越优型评估指标可构造如下联系度函数：

1）第i 个评估指标为I 级

2）第i 个评估指标为II 级

3）第i 个评估指标为III 级

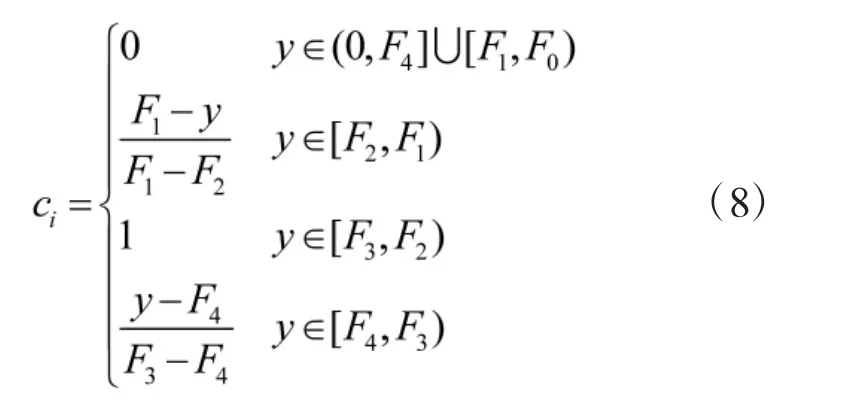
4）第i 个评估指标为IV 级

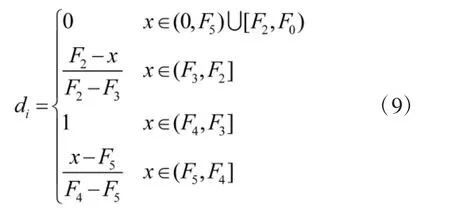
5）第i 个评估指标为V 级

在上述各式中，F0～F5分别为目标威胁度评估指标各级别的界限值；y 为目标威胁度评估指标数据；i 为评估指标序号。同理，可确定越小越优型指标对应的联系度函数。

计算出第i 个评估指标5 个等级的联系度ai，bi，ci，di，ei后，就可得到该指标的同异反向量

计算所有评估指标的同异反向量，就可构建所有评估指标的同异反系数矩阵

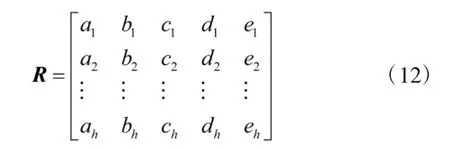
式中，h 表示评估指标个数，本文中h=7。由此建立评估对象的同异反向量计算表达式

4 仿真分析

仿真计算过程分为两个部分，第1 部分利用专家知识对地面时敏目标威胁度进行SPA 评估，构造IELM 的训练和测试样本；第2 部分采用获取的样本训练地面时敏目标威胁度IELM 评估模型，并完成模型测试。

确立地面时敏目标威胁度评估体系和评估流程，就可以结合无人机对地攻击的具体实际，对地面时敏目标威胁度进行评估。表2 为标准化处理后的地面时敏目标威胁度评估指标数据。

表2 地面时敏目标威胁度评估指标数据

地面时敏目标威胁度评估指标体系中的部分指标的分级标准见表3。

表3 地面时敏目标威胁度部分评估指标分级标准

表中I、II、III、IV、V 分别表示特别严重威胁、严重威胁、重大威胁、一般威胁、轻微威胁。对于可靠性 指 标 来 说，“>0.95”、“0.95”、“0.90”、“0.85”、“0.80<”分别代表可靠性的评估等级：I 介于（0.95，1］，II 介于（0.90，0.95］，III 介于（0.85，0.90］，IV 介于（0.80，0.85］，V 介于［0，0.80］区间，余下评估指标的分级标准同理。

确定了指标分级标准，就可根据式（6）～式（10）计算ID 01 可靠性Pr指标的5 个等级的联系度，进而得到Pr的同异反向量表达式

那么，通过同样过程，不难构造ID 01 所有评估指标的同异反系数矩阵

接着通过层次分析过程（AHP）［12］，计算出指标Pr，Ps，Pf，Pd，Pk，Pt，Nu的权重向量w=［0.093，0.148，0.135，0.217，0.064，0.316，0.028］。根据式（18），就可以确定ID 01 的同异反向量表达式

按照均分取值原则，差异度可取为

此处由于i2=0，带入式（18）中，会导致该分项始终为零，丧失该项的贡献力，为避免此种情况，取i2=0.01，这样既能避免该项为零，又使自身的变化影响较小。这样，就可以确定

将E 代入ID 01 的同异反向量表达式，即可计算ID 01 的μ1值为0.736，该值即为ID 01 的地面时敏目标的威胁度。同理，也可得到ID 02～ID 20 的目标威胁度，如表4 所示。

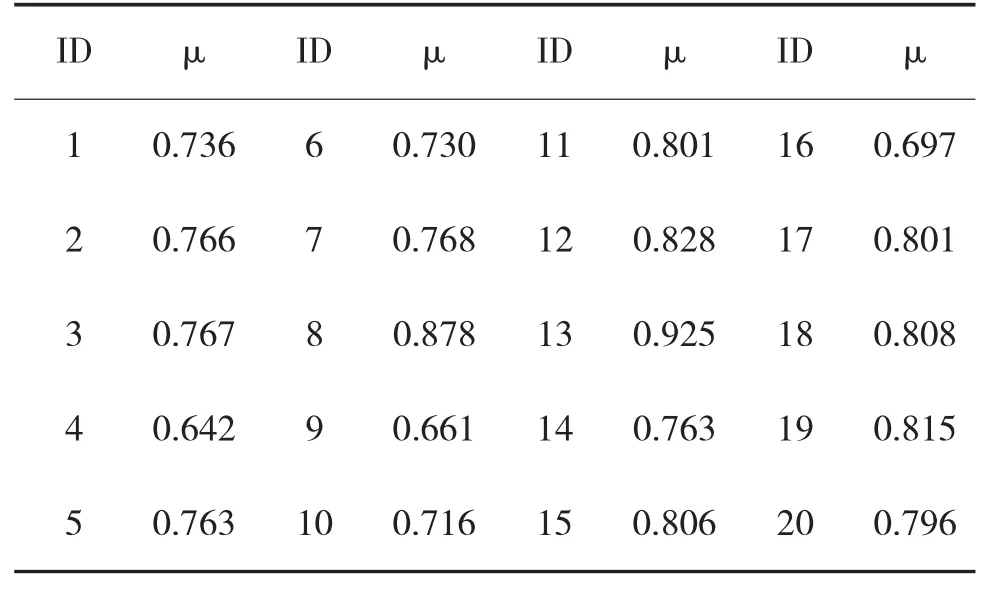
表4 地面时敏目标威胁度值

将表2 的评估指标数据与表4 中对应的目标威胁度逐一组合，就形成了IELM 建模的20 组数据样本。本文采用数据滑动窗方式构建训练样本集和测试样本集，且训练样本集选取16 组数据样本，余下4 组用于测试，如表5 所示。

表5 目标威胁度评估ELM 建模数据样本构造

利用IELM 对以上样本进行处理，对地面目标进行威胁度评估建模，得出目标威胁度值的大小，根据目标威胁度排序，确定优先攻击威胁度大的地面目标。

引入绝对相对误差Err 对预测效果进行分析

式中，y 为由SPA 计算出的目标威胁度，y' 为由IELM 模型得出的目标威胁度。

如选取样本集编号SD 01 和SD 02，观察对应的ELM 模型测试结果与SPA 得出μ 值的对比，结果如表6 所示。

表6 部分计算结果及误差分析

在SPA 构建的评估样本基础上，建立ISVM 威胁度评估模型［13-14］，并与IELM 模型进行比较，以验证ELM 模型的先进性。

由下页表7 可知，IELM的平均训练时间为0.275 s，平均测试时间为0.021 s，SVM 的平均训练和测试时间分别为5.562 s 和0.045 s，在训练时间上，IELM 与SVM 相差了两个数量级，而这一点对无人机攻击决策问题来说尤为重要；IELM 的平均测试Err 在［0.298%，0.574%］区间变动，平均测试Err 为0.402%，SVM 的平均测试Err 在［0.397%，0.731%］区间变化，平均测试Err 为0.518%。IELM 与SVM的测试精度较为接近。

表7 ISVM 与ELM 时间及测试精度对比

从评估结果可看出，SPA 与IELM 的评价结果极为吻合，但与前者相比，基于IELM 的评估方法更具优势，有以下3 点：1）IELM 通过对大量数据训练与学习，找到输入与输出变量之间的非线性关系。模型仅需要一个新样本信息，根据模型内存储的知识进行演绎和推理，就能得出评估结果，虽然比SPA计算复杂，但借助于计算机，反倒简化了评估过程，也为无人机攻击决策节省了时间。2）IELM 可根据训练样本自动调整各指标的权重，避免了如SPA 预先根据专家知识确定权重等主观因素对评估结果的影响，克服了各指标权重随时间动态变动的问题。3）IELM 评价模型泛化能力强，可以通过对历史信息的学习，直接可以对新样本进行处理，给出较合理的威胁度评估结果，SPA 在评估过程中依赖专家知识，主观性过强。因此，将SPA 与IELM 有机结合起来，进行无人机对地目标威胁度评估，不仅利用了IELM 在线评估的优点，还有效解决了训练样本的来源问题。

5 结论

本文针对地面目标威胁度评估指标体系，首先通过SPA 方法生成训练样本和测试样本，然后，采用IELM 建立了空对地时敏对目标威胁度评估模型，实现对多地面目标的威胁度进行排序，由此确定无人机火力系统攻击优先度。仿真表明，所提出方法能够在线训练，精度高，速度快，模型输出与SPA 的评估结果非常吻合。克服了传统方法的人为主观性、无法在线建模、泛化能力不强等缺点，即使对于新样本数据，评估模型也能通过训练模型参数，给出较为准确的评估结果，这有利于无人机快速合理地进行空对地多目标攻击决策。