思政角度下谈高等数学中建模思想的渗透与引导
——理论联系实际的桥梁
王 丹 郝志峰
(济南大学数学科学学院 山东·济南 250022)
1 研究现状
为了发挥数学课程的育人作用,从思政的角度探讨建模思想在高等数学教学过程中的渗透与引导对学生创新能力、思想道德以及科学精神等方面的影响。随着现代科技的迅猛发展,数学的应用已经渗透到生产生活的方方面面。因此,培养学生将实际问题转化为数学问题的能力,对其综合素质和创新能力的提高具有非常重要的促进作用。
高等数学作为理工科专业的必修课之一,在大学新生的课程中占有举足轻重的地位。但是实际的教学过程中因为课时、讲授内容等方面的制约使得课堂上以讲解为主,习题以概念、计算的练习为主。很多与实际相关的例题、习题经常被略过,这一现象使学生在遇到实际问题时,常常感到“力不从心”,不知该如何下手。因此,为了提高大学生正确认识问题、分析以及解决问题的能力,利用好高等数学的课堂,向学生渗透“建模思想”,对其未来学习以及实践具有长远的影响。
数学模型的建立将实际问题与理论分析有机的结合在一起,将实际的研究对象与拟达到的目的通过其内在的规律,以及适当的假设和简化,用数学符号、关系式和定理等形式表达成实际问题中涉及的数量关系以及空间构型的一种数学语言。
2 数学建模思想引入高等数学学习的重要性
2.1 有助于激发学生学习的积极性,提高教学效果
在教学过程中,适当引入一些与实际生产生活相关的例子,可以激发学生的积极性。如在高等数学概念课讲授中,因为相关知识理论性较强,相对有些枯燥,致使教学效果不太理想。因此在讲授该部分内容时,可以加入一些数学发展史的内容,使学生了解其重要性。比如在讲微积分时可以给学生讲授其发展历史,从最初的解决天文学中的三体问题到现在其对力学、机械制造乃至医学中影像、CT等发展的影响;在讲授导数定义时,介绍现在列车电子屏上显示的实时速度等,可以提高学生对该部分内容学习的积极性,对真正的掌握微积分的概念奠定基础,为相关的实际问题解决所蕴含的建模思想有一定的认识。
2.2 有利于提高学生的创新思维和创新能力
数学建模思想的建立是一个理论与实践相结合、协同发展的具有创造性的思维过程。在具体问题的解决中,学生根据自身的知识储备,会迸发出不同的思维火花,我们要保护学生这种创新思维的种子,引导他们最终通过自己的知识构架解决问题,从而提高学生的创新思维和能力。
2.3 提高学生正确认识问题、分析问题和解决问题等方面的综合能力
建模思想的建立对学生解决实际问题有非常重要的作用。学生在初步体会了建模思想带来的趣味后,会将其尝试着用到其他相关问题的解决中。建模思想的树立和应用将全面提高学生在认识问题、分析问题和解决问题等综合能力。
3 “建模思想”的实施建议与策略
建模过程具有逻辑性,该思想的渗透与引导需要一定的策略来实现:
(1)利用课上宝贵时间,在新内容讲授前通过案例分析,引导学生以建模的思想理解、掌握新知识;使学生建立统筹的格局观、认识观。向学生介绍建模思想,鼓励学生挖掘其内部的隐含关系;以问题引导学生积极思考。在课程结束总结时,引导学生捋清建模思想涉及的整个过程,让学生真正体会到站到不同角度看问题的好处,该种思想的逐步确立将对学生今后的学习、工作起到一定的潜移默化的作用。
(2)课下积极向学生介绍相关资料与读物,拓展学生的知识面,让学生认识到高等数学是看得见、摸得着、用得上的“好玩”的知识,对解决实际问题有非常重要的作用,从而激发学生学习的兴趣。
(3)以教学月为单元,向学生抛出与本月学习内容相关的建模问题,设置开放性的答案,采取小组合作的方式,鼓励学生开展小组内的沟通与交流,并记录下其中遇到的问题以及解决方法,最后总结不同的建模方法。
4 具体案例的剖析
高等数学中微积分、函数的最值问题、常微分方程的求解等内容都渗透着丰富的哲学、数学思想。思政背景下,引导学生发掘其内在的建模思想对培养学生的创新思想、大国工匠精神具有非常重要的作用。
4.1 一元定积分积分问题
定积分思想中蕴含了丰富的哲学思想,即“化零为整”的由局部到整体,由量变(近似、求和)达到质变(取极限)的辩证法思想,且与我国古代数学家刘徽的“割圆术”的思想切合。让学生认识到积分是为了解决从变力做的功和求曲边梯形的面积等实际问题中抽象出来的。在遇到实际问题时,可以采取“分割、近似、求和、取极限”的建模思想对其进行研究。
例1:每天用到的手机、电脑都会显示实时的网速,如何确定在时间段t=[0,1]内消耗的总流量。设网速与时刻t的关系满足,如图曲线所围成的面积即为该时间段内消耗的流量。引出求曲边梯形的面积问题,如图1所示,同时介绍以直代曲、近似、求和、取极限的模型思想,引导学生思考图形的划分问题。将区间[0,1]进行n等分,并用小矩形左侧点的函数值近似代替矩形的高度,则有如下的近似关系:

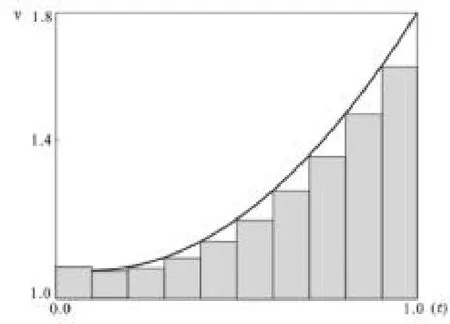
图1:曲边梯形的分割
在此基础上,给出定积分的定义,更有利于学生理解。同样的在讲授多重积分时,会采用同样的建模思想,便于学生理解掌握。
4.2 微分方程思想在证明题中的应用

4.3 一元与多元函数的最值问题
5 结论
因此,在实际教学活动中,要重视建模思想的渗透与引入,将会激发学生的学习兴趣,提高教学效果,此外对提高学生的抽象思维、逻辑推理能力以及解决实际问题的能力都有非常重要的影响。从思政的角度,也培养了学生的综合能力,为其未来发展打下良好的基础。

