红外光谱数据融合结合化学计量学无损检测汽车灯罩
卫辰洁,王继芬*,曾啸虎
(1.中国人民公安大学 侦查学院,北京 102600;2.酒泉卫星发射中心,甘肃 酒泉 735000)
目前,交通肇事逃逸案件时常发生,居高不下,不仅扰乱了交通秩序和社会治安秩序,而且对人民的生命财产安全造成了严重威胁。在此类案件现场,通常留有汽车灯罩碎片等物证,通过对灯罩碎片进行检验,可以为侦查人员提供线索,起到辅助证实或否定嫌疑的作用。
汽车灯罩分为前灯和尾灯灯罩,主要以聚碳酸酯(PC)、聚苯乙烯(PS)和聚甲基丙烯酸甲酯(PMMA)3种材料注塑而成[1-3]。PC注塑的灯罩抗紫外线、透光性好,因长时间使用后颜色不变,在汽车灯罩中的应用最为广泛[4];PS由于成型性好、低吸湿性以及价格低廉,被部分汽车厂商用作汽车灯罩材料;PMMA材料具有优良的光学性能,透光率高达93%[5],比一般玻璃等材料的透光性能优异,质轻,常用来制造汽车尾灯灯罩。而材料的差异性以及不同厂家加工方式的不同为汽车灯罩的检验鉴别提供了前提条件。
傅里叶变换红外光谱(Fourier transform infrared spectroscopy,FTIR)作为一种光谱分析技术,具有灵敏度高、测量速度快、对检验样本无损等特点,在石油化工[6]、材料科学[7-8]、生物[9]、医药[10-11]和环境[12]等领域被广泛应用。其原始光谱和导数光谱均具有独特优势[13-16],相互融合可以更准确地描述物质特征。但目前将原始光谱与导数光谱相结合的光谱融合技术的相关报道较少。化学计量学作为一门新兴的交叉学科,与光谱分析技术相结合,可以优化实验测量,有效提取实验数据[17-20]。
基于快速、无损、准确的检验目的,本实验采用傅里叶变换红外光谱结合化学计量学方法对汽车灯罩进行分类,比较了单独的原始光谱、一阶导数光谱和融合光谱数据的分类效果,以实现对汽车灯罩物证的准确检验,为光谱融合技术在分析检测领域的应用提供借鉴和参考。
1 实验部分
1.1 主要原料
实验共收集汽车灯罩检材44个,其中汽车前灯灯罩14个,尾灯灯罩30个,包括PC、PS和PMMA 3种材料成分,涉及北京现代、东风、丰田、远景、吉奥、哈飞、海马、江铃、比亚迪、五菱、奇瑞和长安12个品牌。
1.2 实验方法
样本预处理:将44个汽车灯罩样本用酒精擦拭,并对样本进行对应编号,做好样本的统计和整理。
光谱数据采集:采用傅里叶变换红外光谱仪及其附件(Thermo Fisher Scientific公司),以空气为背景进行光谱采集,设置温度为(24±2)℃,相对湿度为58%[16],分辨率4 cm-1,采集范围4 000~400 cm-1,扫描次数32次。每个样本均采集3次光谱曲线,取均值作为最终数据[21]。采用自动基线校正、峰面积归一化、Savitzky-Golay算法平滑3种方法进行预处理,并对44个样本的光谱分别做一阶差异导数处理,保存原始光谱与导数光谱数据。
1.3 实验建模
K近邻(K-Nearest neighbor,KNN)算法是一种思想简单、但计算复杂的分类算法。其具体思想是,用已准确分类的样本为模型,通过计算未知样本与模型样本数据之间的距离,来判断样本所属类别。算法中的K值为选取的最近距离的K个模型数据。例如,当K值取3时,选取最近的3个模型数据。若其中2个模型数据属于A类样本,1个模型数据属于B类样本,则判断该样本为A类。因此,K值的选取对KNN模型分类结果有很大的影响。通常情况下,采用交叉验证等方法来选取最优的K值。
Fisher判别分析(Fisher discriminant analysis,FDA)是通过寻找合适的投影方式,建立相应的线性判别函数,使得投影后同一类别的判别函数值f(x)差异极小化,而不同类别的判别函数值f(x)差异极大化。一般情况下,判别函数表达式为:

式中CT j为判别系数,X为自变量,m为观察指标,j为对m个观察指标的不同系数进行标识。通常Fisher判别会建立一个或多个判别函数,逐例计算出判别函数值f(x),即判别得分。根据样本设置的类别数,结合判别得分可以制定出对应的判别规则,最终实现对样本的准确分类。
2 结果与讨论
2.1 模型构建
以PC、PS和PMMA 3种材料成分为依据,分别对44个汽车灯罩样本的原始光谱、一阶导数光谱和融合光谱数据构建KNN和FDA两种分类模型。在KNN模型中,运用训练样本即为测试样本的方法进行交互验证[22],并通过交叉验证的方法选取每组数据中最优的K值,从而减少误判样本,提高总体分类准确率。
图1中的A、B、C分别为原始光谱、一阶导数光谱和融合光谱数据的K值选择错误统计图,展示了K值在1~20之间的错误率。从图中可以看出,对于原始光谱数据,在K值选择小于8时,错误率上下浮动较大,且在K值为1时错误率最低,达到0.37。当K值选择大于8后,错误率稳定在0.39不变,因此选择K=1作为44个汽车灯罩样本原始光谱数据的最优K值;对于一阶导数光谱数据,K=1时的错误率最高,K值选择3和6时错误率为0.40,K=4时错误率最低,为0.32,其余均为0.35,故选择K=4作为一阶导数光谱数据的最优K值;对于融合的光谱数据,K=4时错误率最低,为0.41,其余K值选择错误率均在0.45以上,故以K=4作为融合光谱数据的最优K值。
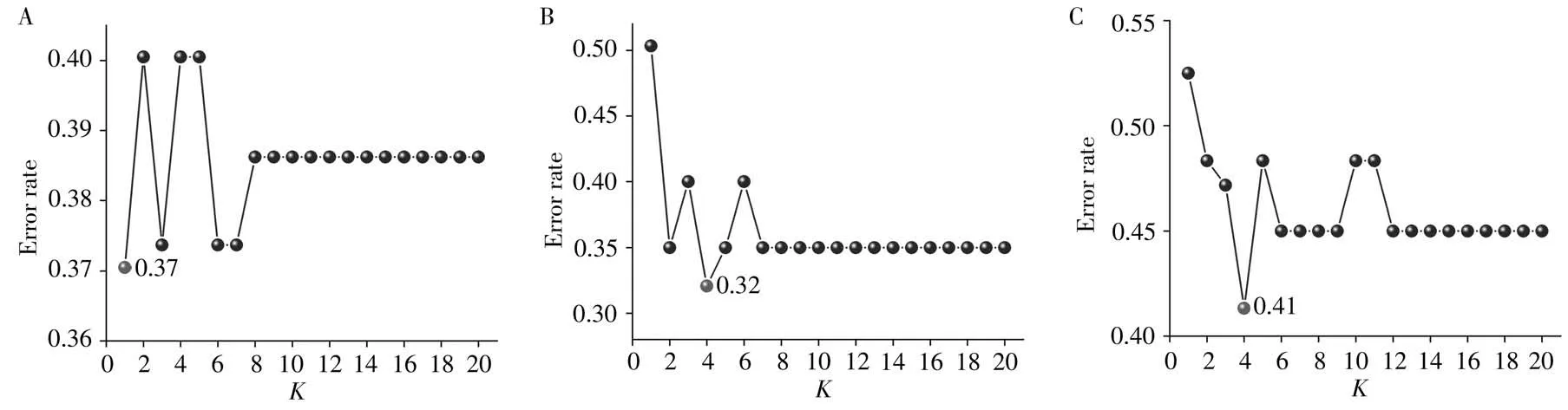
图1 分类错误率随着K值的变化图Fig.1 Graph of classification error rate as K value changes A.original spectra;B.first derivative spectra;C.fusion spectra
表1展示了原始光谱数据、一阶导数光谱数据和融合光谱数据在KNN和FDA两种模型下的分类准确率。可以看出,在KNN模型中,总体分类准确率均较低,最高仅有63.60%。分析认为,由于KNN模型受到样本不均匀的影响,即在44个汽车灯罩样本中,存在28个PC样本,11个PMMA样本和5个PS样本,PC样本数远大于另外两个样本,导致KNN模型判别时将更多的样本误判为PC样本。在FDA模型中,基于原始光谱数据、一阶导数光谱数据和融合光谱数据的PS样本均实现了准确分类,分类准确率为100.00%。相对于PS样本,另两类样本的分类准确率较低。对单独的原始光谱数据、一阶导数光谱数据和融合光谱数据的分类准确率进行比较,发现融合后的光谱数据构建的FDA模型分类准确率更高,PMMA、PC、PS样本的分类准确率分别达到81.80%、96.40%和100.00%,总体分类准确率为93.20%,实验结果较为理想。但个别样本的误判仍然会对法庭科学领域汽车灯罩的检验产生影响,因此实验对分类模型进一步优化,以获得更高的分类准确率。
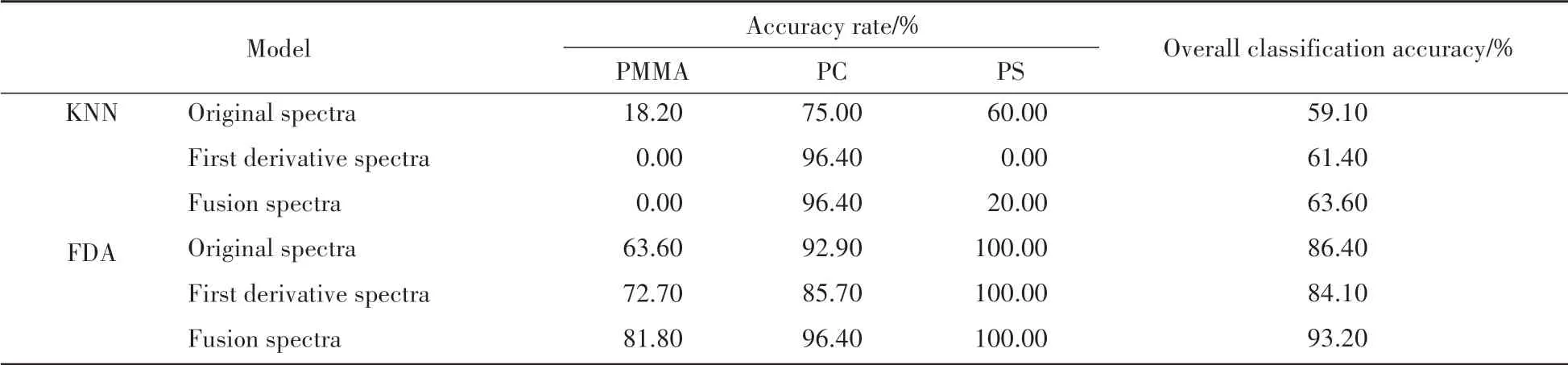
表1 不同分类模型下的结果对比Table 1 Comparison of results under different classification models
2.2 模型优化
主成分分析(PCA)作为一种统计学方法,可以通过正交变换的方式改变数据间的多重共线性问题。尤其是面对大量的样本数据,采用PCA可以有效地提取数据主要成分,将多维度的相关性变量转化为低维度的线性不相关变量。并可通过这些提取的变量反映原有变量的绝大部分信息。实验中,每组数据均存在大量的变量,因此采用PCA对原有数据进行降维。
图2和图3为原始光谱数据的PCA分类结果。其中,“特征根”与主成分一一对应,可以表示该主成分解释方差的大小;“方差贡献率”指对应成分方差与总方差的比值,可以反映该成分对原始变量解释程度的大小;“累积方差贡献率”是前N个主成分的方差贡献率之和。一般情况下,在选取主成分时应选择能够解释原始变量方差比例高的作为主成分。通常有两个判断标准,一方面要求成分的特征值大于1;另一方面要求累积方差贡献率大于85%[21]。从图2及图3可知,对于原始光谱数据的PCA结果,前11个成分的特征根均大于1,累积方差贡献率达到99.41%,满足判断标准,可以解释原始变量99.41%的信息,即能够较好地反映原始变量信息。

图2 原始光谱前11个主成分的方差贡献率Fig.2 Variance contribution rate of the first 11 principal components of original spectra
相同判断标准下,对一阶导数光谱数据和融合光谱数据进行PCA降维。一阶导数光谱数据提取了13个主成分,累积方差贡献率达到85.51%,可以解释原始变量85.51%的信息;融合光谱数据提取了7个主成分,累积方差贡献率达到86.13%,可以解释原始变量86.13%的信息。结果表明,对汽车灯罩样本的原始光谱数据、一阶导数光谱数据和融合光谱数据的主成分分析效果理想。
分别对利用PCA降维后的原始光谱数据、一阶导数光谱数据和融合光谱数据构建KNN和FDA分类模型。在KNN模型中,交叉验证分别选择K=3、2、10作为原始光谱数据、一阶导数光谱数据和融合光谱数据的最优K值。
表2展示了原始光谱数据、一阶导数光谱数据和融合光谱数据在PCA+KNN和PCA+FDA两种优化模型下的分类准确率。与PCA降维之前的分类结果相比(表1),两种模型的分类准确率均有提高。分析认为,采用PCA对原有数据进行降维,可以有效消除原有数据的冗余信息,减小原有变量之间的相关性,实现用更少的变量反映原有多维度变量信息的目的。并且,数据量的缩减也加快了模型构建的速度,满足快速准确的检验需求。在构建的PCA+FDA分类模型中,相比单独的原始光谱数据和一阶导数光谱数据,基于融合光谱数据的分类准确率更高,对PMMA和PS两种样本均实现了100.00%的准确分类。对PC样本的分类准确率为96.40%,即28个PC样本中,误判1个样本。总体分类准确率达到97.70%,实验结果理想。在构建的PCA+KNN分类模型中,整体分类准确率低,融合后的光谱数据也未显示出明显优势,进一步证明KNN模型受到了样本数量不均匀的影响。

表2 不同分类模型下的结果对比Table 2 Comparison of results under different classification models
图4是PCA+FDA模型下的判别函数,A、B、C分别展示了原始光谱数据、一阶导数光谱数据和融合光谱数据在PCA+FDA模型构建的判别函数下的分类情况。可以看出3组数据下,PS样本均与其他样本间隔较远,实现了全部分类。而PMMA和PC样本存在一定程度的交叉,出现误判。对图4的A、B、C进行比较,可以发现,基于融合后的光谱数据构建的PCA+FDA模型分类情况明显优于单独的原始光谱数据和一阶导数光谱数据。
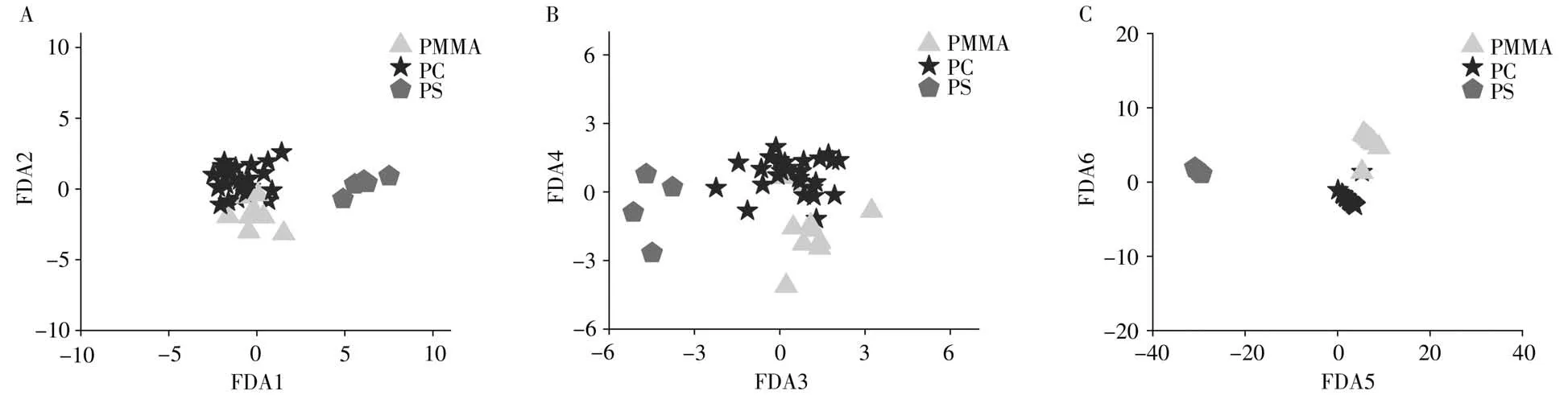
图4 PCA+FDA模型的判别函数图Fig.4 Discriminant function diagram of PCA+FDA model A.original spectra;B.first derivative spectra;C.fusion spectra
采用融合后的光谱数据构建的PCA+FDA模型对44个汽车灯罩样本的12种品牌进行分类,分类准确率达到100.00%,实现了对品牌的准确区分,结果理想。
3 结 论
本文构建了可对汽车灯罩进行分类的KNN和FDA两种模型,发现FDA模型的整体分类准确率较高,在原始光谱数据、一阶导数光谱数据和融合光谱数据下的分类准确率分别达到86.40%、84.10%和93.20%,而结合PCA后的FDA模型对样本的分类准确率更高,在原始光谱数据、一阶导数光谱数据和融合光谱数据下的分类准确率分别达到88.60%、90.90%和97.70%。表明利用PCA方法可以实现对原有数据信息的提取,排除冗余信息,达到优化模型分类效果和提高模型分析速度的目的。对单独的原始光谱数据、一阶导数光谱数据和融合光谱数据构建分类模型,比较发现基于融合光谱数据构建的分类模型分类准确率更高,在FDA模型中,融合后的分类准确率达到93.20%。采用PCA+FDA模型对12种品牌的44个汽车样本进行区分,分类准确率达到100.00%。结果表明,融合后的光谱数据可以结合原始光谱和导数光谱各自的优势,获取更多的样本信息,从而对汽车灯罩样本实现更准确的分类。

