构建变化电路中的方程组思想

吴玉茹

◆摘  要：：中考物理电学综合题，考查的知识面广、难度大，有时无法利用分步求解，构建变化电路中的方程组来求解变化电路中的物理量，起到化繁为简、化难为易、化抽象为具体的作用。这类题的特点是电路变化频繁，未知量多、综合性强、形式多样、求解过程复杂，是中考电功率最常见的题型之一。本文以构建变化电路中的方程组思想为题，谈谈如何列方程组求解电学综合题。要

◆关键词：变化电路;列方程组

变化电路是指电路的控制条件发生改变时，电路中的电流、电阻、部分电压发生相应改变的电路。这类问题，由于控制的条件不同，电路所处的状态就不一样。因此，化解这类问题，首先要分析电路的状态，找出不同状态下的变化量、已知量和待求量，寻求三者间的等量关系，以此建立方程组，来得以解决问题，这种解决问题的方法称之为方程组思想。

一、列方程组的条件

1.从未知量看：当电路存在两个或两个以上的未知量，需要列方程组。

多数时候题目中没给出电源电压某电阻阻值，它们是所要求未知量或未知量的一部分。当一个题目含较多量时，即涉及到的量（包括已知量与未知量）较多较复杂时，常常采用的方法。

2.从电路状态看：当电路存在两种或两种以上状态，需要列方程组。

在对应电路某种状态的一个等式中常会出现两个（或两个以上）未知量，按常规方法不能求出待求量，在这种情况下，对应电路两种状态列方程组是解决问题的基本方法。

二、列方程组的关键

选择恰当的物理量参与列方程组，选择不当会徒增未知量，造成无法求解的局面。参与列方程组的物理量可以是不变量的未知量，可以是已知量，也可以是待求量。列方程组的关键是找不变量、已知量或等量关系。

1.紧扣题中的不变量（电源电压或定值电阻）列方程组。

形式：①U=IR     ②U=U1+U2

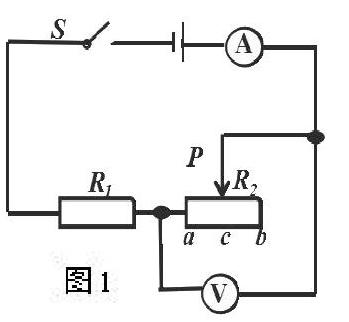
例题：如图1所示的电路中，电源电压不变，R1为定值

电阻，R2为滑动变阻器。闭合开关S后，当滑片P在a、b

之间某个位置时，电流表的示数为0.4A，电压表的示数为4V。

当滑片P在b端时，电流表的示数为0.2A，电压表的示数为8V。

求：电源电压和R1的阻值。

分析：此题的变式在于已知量以图象展示，要从图像中获取两种状态下的电流I和R2消耗的电功率P2为已知量。此题电路中滑片P的移动，电路发生了两次变化，给出两种状态下已知量I和U2。构建以不变量U为中心的方程组。利用串联电路电压特点、欧姆定律相结合，用已知量I、未知量R1代替不求的未知量U1，用已知量U2列出方程組求解。

解：当P在a、b之间某个位置时，电流表的示数为I=0.4A，电压表的示数为U2=4V。

当P在b端时，电流表的示数为I'=0.2A，电压表的示数为U'2=8V。

U=IR1 + U2

U= I' R1 + U'2

代入数据

U=0.4A R1 + 4V -------------------------------（1）

U= 0.2AR1 + 8V  -------------------------------（2）

联立（1）、（2）解得：U=12V，R1=20Ω

所以，电源电压为12V，R1的电阻是20Ω。

三、结束语

本文详细探讨了变化电路中的方程组思想的构建，等效替代思想在列方程组解应用题发挥了重要的作用。构建变化电路中的列方程组思想来分析电路的过程， 把抽象、繁琐的问题转化成简单、直接等式。由此可见，方程组思想巧解变化电路中的物理量，有效解决一些常规物理方法难以解决的问题，达到事半功倍的效果。同时优化课堂教学、提高课堂教学效率，拓展学生思维的空间、丰富学生解题的方法，提高应变的能力，有着重要意义。