水浮力作用下主裙楼一体结构地基承载力验算分析

杨艳春

(郑州大学综合设计研究院有限公司，郑州 450002)

0 引言

目前建筑工程中存在大量的主裙楼一体的结构，当地下水位处于基底以下时，按照文献[1]确定的基本原则：对于主体结构地基承载力的深度修正，宜将基础底面以上范围内的荷载，按基础两侧的超载考虑，当超载宽度大于基础宽度两倍时，可将超载折算成土层厚度作为基础埋深；当基础两侧超载不等时，取小值。设计师能够相对容易地掌握主裙楼地基承载力验算的方法。但是对于大多数地下工程而言，地下水位一般均位于基底以上，主裙楼均受到水浮力的作用。如何考虑水位变化对基底压力以及地基承载力的影响，设计师采用的方法各不相同且计算结果相差较大。尤其是当地下水浮力大于裙房自重时，由于文献[1]中缺少相关内容的规定，许多设计师习惯上不再考虑地下水浮力作用或者按地下水浮力与裙房自重相等时的水位考虑，对地下水位变化对地基承载力影响的认识也比较模糊。

针对以上问题，在考虑地下水浮力作用的条件下，本文对主裙楼一体结构的地基承载力计算公式进行推导和换算，换算后的公式便于更加直观地了解地下水位变化对地基承载力验算的影响。

1 主楼周边为回填土时地基承载力验算

文献[1]第5.2.1条及第5.2.2条规定，当轴心荷载作用时，基础底面的压力，可按下列公式确定：

pk≤fa

(1)

(2)

式中：pk为相应于作用的标准组合时，基础底面处的平均压力值，kPa；fa为修正后的地基承载力特征值，kPa；Fk为相应于作用的标准组合时，上部结构传至基础顶面的竖向力值，kN；Gk为基础自重和基础上的土重，kN；A为基础底面面积，m2。

文献[1]第5.2.4条规定，当基础宽度大于3m或埋置深度大于0.5m时，从载荷试验或其他原位测试、经验值等方法确定的地基承载力特征值，尚应按下式修正：

fa=fak+ηbγ′(b-3)+ηdγm(d-0.5)

(3)

式中：fak为地基承载力特征值，kPa；ηb为基础宽度的地基承载力修正系数；γ′为基础底面以下土的浮重度，kN/m3；b为基础底面宽度，m，当基础底面宽度小于3m时，按3m取值，大于6m时，按6m取值；ηd为基础埋置深度的地基承载力修正系数；γm为基础底面以上土的加权平均重度，kN/m3，位于地下水位以下的土层取有效重度；d的含义见图1。

文献[1]对式(1)两侧基础上的土重论述不同：计算式(1)左侧基底压力时，对基础上的土重没有做出明确规定；计算式(1)右侧地基承载力特征值时，规定位于地下水位以下的土层取有效重度。

文献[2]第5.3.2条规定Gk为基础自重和基础上的土重之和，在稳定的地下水位以下的部分，应扣除水的浮力，kN。

由于地下水对式(1)两侧的作用是同时存在的，所以本文参照文献[2]的规定计算。

某有多层地下室的建筑物，建筑周边为回填土，稳定水位位于室外地面以下d1处，见图1(a)。根据文献[2]中Gk的定义，计算基底压力时应扣除水的浮力γwd2，式(1)可改为：

pk-γwd2≤fa

(4)

根据图1(a)，基础底面以上土的加权平均重度γm可换算为：

图1 单体结构及主裙楼一体结构示意图

(5)

式(3)和式(5)代入式(4)可换算为：

pk-γwd2≤fak+ηbγ′(b-3)+

(6)

2 主楼周边为地下室裙房时地基承载力验算

2.1 裙房作用于基底的压力不小于基底水浮力

pk-γwd2≤fak+ηbγ′(b-3)+

(7)

pk-γwd2≤fak+ηbγ′(b-3)+

(8)

pk≤fak+ηbγ′(b-3)+ηd(p0k-

(9)

当γwd2=0，式(8)可换算为：

pk≤fak+ηbγ′(b-3)+ηd(p0k-0.5γ)

(10)

当p0k-γwd2=0，即裙房作用于基底的压力与作用于基底的水浮力相等时，式(8)可换算为：

pk-p0k≤fak+ηbγ′(b-3)

(11)

pk≤fak+ηbγ′(b-3)+p0k

(12)

2.2 裙房作用于基底的压力小于基底水浮力

2.2.1 地下水对基底以下土的浮重度的影响

根据图2，取d2=d3+d4及γwd3A0=p0kA0，作用于基底水浮力Ff=γwd2A0=γwd3A0+γwd4A0。设计时应布置抗浮锚杆等以便平衡超出裙房自重的水浮力γwd4A0。作用于锚杆顶部的上拔力，通过锚杆与土之间的粘结作用，假定沿锚杆高度范围近似均匀地施加于桩间土内，土的平均重度会小于浮重度，而基底土压力始终保持为0。本文引入土的浮重度调整系数μ1，用μ1γ′表示考虑浮重度调整系数μ1后的基底以下土的重度。其中μ1按下式计算：

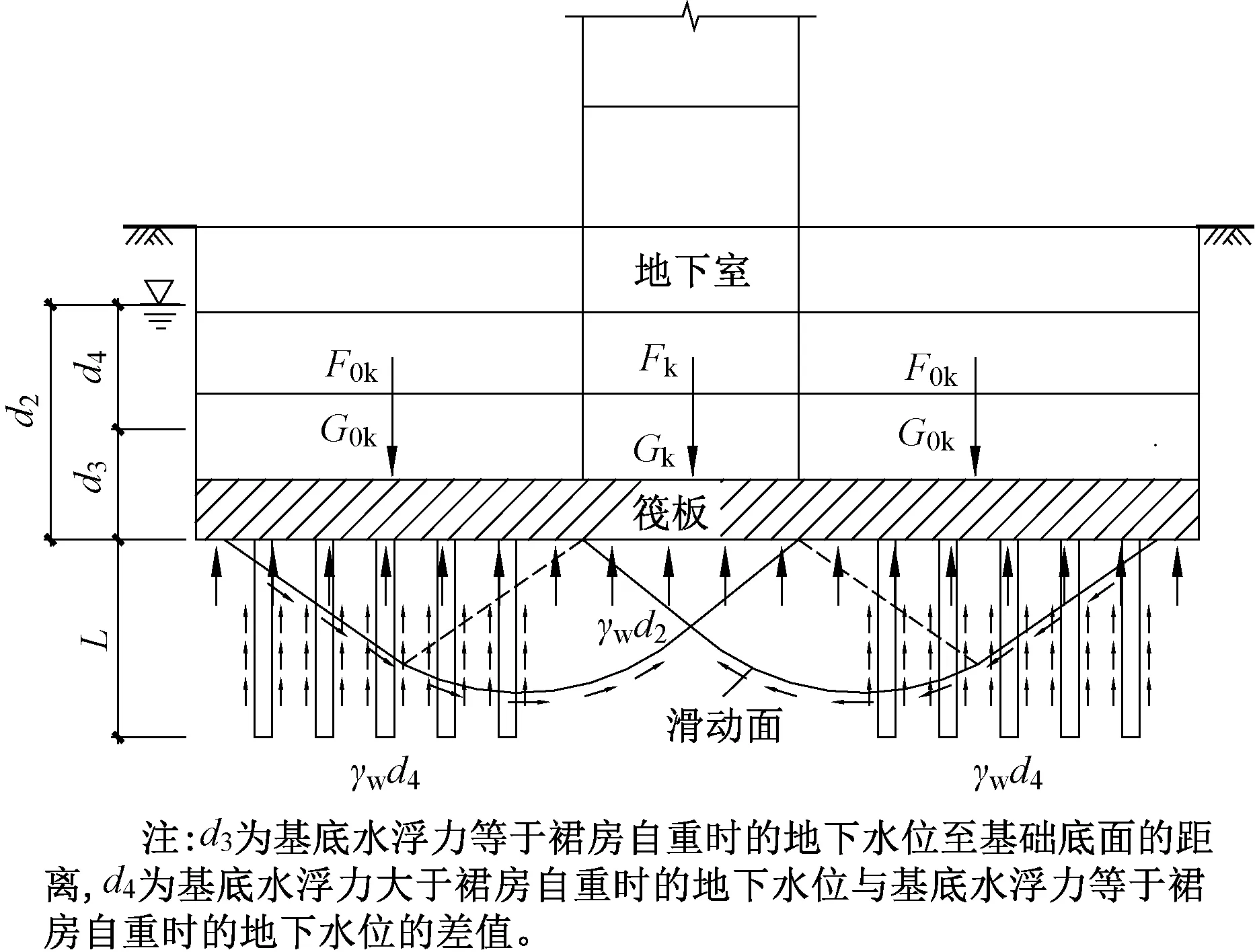
图2 主裙楼一体结构抗浮锚杆整体稳定计算示意图

(13)

式中L为抗浮锚杆的长度，m。

根据文献[3]第11.2.4条整体抗浮稳定验算的规定，W+G=KFf，其中W为基础下抗浮锚杆范围内总的土体重量，计算时采用浮重度；G为结构自重及其他永久荷载标准值之和；K为抗浮稳定安全系数。W=γ′LA0，G=p0kA0，换算得：

γ′LA0+p0kA0=Kγwd2A0

γ′LA0=Kγwd4A0+(K-1)γwd3A0

由于K≥1.0时，基础下锚杆范围内总的土体重量γ′LA0≥γwd4A0，将其代入式(13)可得：0≤μ1≤1。

2.2.2 地下水对地基承载力计算的影响

(1)μ1=1时修正后的地基承载力特征值

μ1=1时，地下水位位于d4=0的位置，根据式(11)可知，此时修正后的地基承载力特征值可取式(11)右侧各项之和，并用fa1=fak+ηbγ′(b-3)表示。

(2)μ1=0时修正后的地基承载力特征值

μ1=0时，考虑浮重度调整系数μ1后的土的重度相当于0。此时修正后的地基承载力特征值，可参考文献[1]和文献[4]中的有关规定分别计算。

文献[1]第5.2.4条规定基底水位以下土的重度应取浮重度，并未论述基底水位以下土的重度为0时应如何考虑。本文假定基底以下土的重度0可直接代入式(3)中的γ′，且γm取0时，式(3)可换算为：

fa=fak

(14)

依据文献[1]第5.2.4条规定，式(3)中的fak是依据载荷试验或其他原位测试、经验值等方法确定的。因为试验条件下土的重度一般不会小于土的浮重度，当土的重度为0时，地基承载力特征值是否仍可按照fak取值需进一步研究。式(14)推导假定中仅将γ′作为变量，没有考虑fak取值有可能改变的影响，本文建议宜对式(14)进行修正且参照文献[4]的理论进行调整。

根据文献[4]论述的普朗特尔-雷斯诺及太沙基等极限承载力公式，天然地基极限承载力及修正后的地基承载力特征值计算公式为：

(15)

(16)

式中：fu为地基极限承载力，kPa；Nr，Nq，Nc为地基承载力系数；c为地基土黏聚力；K为安全系数；式(15)、式(16)右边三项依次代表了基底以下一定深宽范围内滑裂土体自重γ、基底以上重量γmd、滑裂面上土的黏聚力c对地基承载力的贡献大小。

本文建议c，Nc/K可分别参照地质勘察报告及《高层建筑岩土工程勘察标准》(JGJ/T 72—2017)附录B提供的参数选用。

当γmd，γm取0，即不考虑基底以上的重量时，式(16)可换算为：

(17)

当土的浮重度调整系数μ1=0，即不考虑基底以下土的重度γ时，式(17)可换算为：

fa=cNc/K

(18)

综上所述，参照文献[1]，推导结果为fa=fak；参照文献[4]，推导结果为fa=cNc/K。两者结果不同，尤其c=0时按照文献[4]推导结果为fa=0，该值与文献[1]计算结果fa=fak差别很大。从安全角度考虑，本文建议μ1=0时，修正后的地基承载力特征值可取cNc/K及fak较小值，并用fa0表示，即：

fa0=min(cNc/K,fak)

(19)

(3)0<μ1<1时修正后的地基承载力特征值

0<μ1<1时，修正后的地基承载力特征值的取值可由fa0和fa1进行插值换算得到，即：

fa=fa0+μ1(fa1-fa0)

=μ1[fak+ηbγ′(b-3)]+(1-μ1)min(cNc/K,fak)

(20)

(4)0≤μ1≤1时地基承载力计算

随着地下水位由d3上升至d3+d4，式(11)两侧应修改为：左侧应减小γwd4，右侧替换为式(20)，此时式(11)可换算为：

(21)

式(13)代入式(21)后，可换算为：

(22)

(23)

当取μ1=0时，式(22)和式(23)可分别换算为：

pk-p0k-γ′L≤min(cNc/K,fak)

(24)

pk≤min(cNc/K,fak)+p0k+γ′L

(25)

当取μ1=0，c=0时，式(24)和式(25)可分别换算为：

pk-p0k+γ′L≤0

(26)

pk≤p0k+γ′L

(27)

工程中一般认为砂土、碎石土的黏聚力c=0，故式(26)和式(27)一般可用于砂土、碎石土。

3 算例

3.1 已知条件

3.1.1 基本条件

主楼周边为多层地下室裙房，基础埋深12m，基础底面宽度20m，裙房作用于基底的压力p0k=60kPa，土的天然重度γ取20kN/m3，水的重度γw取10kN/m3，抗浮锚杆的长度L取10m。

3.1.2 工况定义

地下水位标高取5处且分别定义为工况1～5。具体如下：

工况1：地下水位取与基础底平，即地下水位至基础底面的距离d2=0，采用式(9)或式(10)计算。

工况2：地下水位取基底水浮力与0.5倍裙房作用于基底的压力相等的水位，即地下水位至基础底面的距离d2=3m，采用式(9)计算。

工况3：地下水位取基底水浮力与裙房作用于基底的压力相等的水位，即地下水位至基础底面的距离6m，采用式(9)或式(12)计算。

工况4: 地下水位取基底以下土的浮重度调整系数μ1=0.5时的水位，即地下水位至基础底面的距离d2=11m，采用式(23)计算。

工况5: 地下水位取基底以下土的浮重度调整系数μ1=0.0时的水位，即地下水位至基础底面的距离d2=16m，采用式(23)或式(25)计算。d2=16m大于基础埋深12m，该地下水位实际并不存在，仅用于对比分析使用。

3.1.3 项次定义

项次1～3(表1、图3)模拟黏性土和粉土，分别对应3种不同基础宽度和埋置深度的地基承载力修正系数ηb，ηd。项次1～3均取地基承载力特征值fak=150kPa，并假定cNc/K略小于fak，取cNc/K=100kPa(该值仅用于工况4、工况5的验算)。

项次4、项次5(表1、图3)模拟砂土、碎石土，分别对应2种不同基础宽度和埋置深度的地基承载力修正系数ηb，ηd。项次4、项次5均取地基承载力特征值fak=250kPa,并取c=0(该值仅用于工况4、工况5的验算)。

3.2 计算结果

按照工况1～5所选公式计算的等效地基承载力特征值详见表1、图3，其中等效地基承载力特征值为各工况所选公式的右侧各项之和。

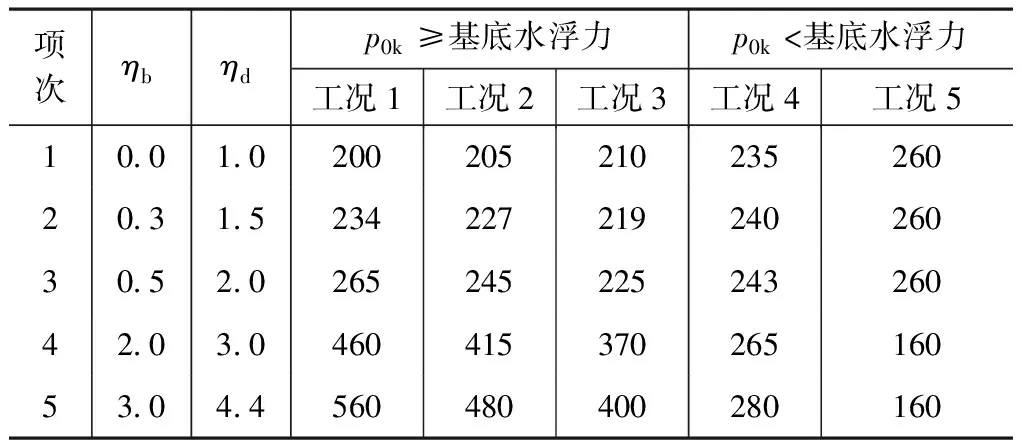
等效地基承载力特征值/kPa 表1

图3 等效地基承载力特征值随基底水浮力变化

3.3 结果分析

(1)工况1～3(地下水位至基础底面的距离d2由0上升至6m的过程)：根据表1及图3，项次1(ηd为1.0)时，地下水位的高度对等效地基承载力特征值的影响不大；项次2～5(ηd大于1.0)时，对于等效地基承载力特征值的计算，地下水均为不利因素。

原因分析：在地基承载力验算时，如果考虑了地下水对基础的浮力，基础底面的压力确实是减小了，对减小荷载是一种有利作用，但在地基承载力计算公式中的基础以上的土体重力也同时需考虑浮力而使地基承载力相应减小了，这对地基承载力的验算来说，是一种不利作用。对于基础埋置深度的地基承载力修正系数ηd为1.0的土层(项次1)，上述不利作用与有利作用基本相互抵消。而对于基础埋置深度的地基承载力修正系数ηd大于1.0的土层(项次2～5)，上述不利作用要大于有利作用；尤其对于基础埋置深度的地基承载力修正系数ηd可取3.0～4.4的土层(项次4～5模拟的砂土、碎石土)来说，上述不利作用要远大于有利作用。表1、图3的计算结果也体现了这一点。

(2)工况3～5(地下水位至基础底面的距离d2由6m上升至16m的过程)：根据表1及图3,项次1～3(模拟黏性土和粉土)时，对于等效地基承载力特征值的计算，地下水为有利因素；项次4、项次5(模拟砂土、碎石土)时，对于等效地基承载力特征值的计算，地下水为不利因素。

原因分析：与工况1～3类似，在地基承载力验算时，如果考虑了地下水对基础的浮力，基础底面的压力确实是减小了，对减小荷载是一种有利作用，但在地基承载力计算公式中的基础以下的土体重力也同时需考虑浮力而使地基承载力相应减小了，这对地基承载力的验算来说，是一种不利作用。另外，本文计算时采用的是μ1=0时的地基承载力特征值fa0=min(cNc/K,fak)，而非fak，这对地基承载力验算来说，亦是一种不利作用，尤其是对于基础持力层为砂土、碎石土的地基。μ1=0时，对于项次1～3(模拟黏性土和粉土)来说，ηb较小，而min(cNc/K,fak)≈fak，考虑了地下水对基础的浮力后，按照式(25)中min(cNc/K,fak)+γ′L计算的值一般不小于按照式(12)中fak+ηbγ′(b-3)计算的值，对于黏性土和粉土地基承载力的验算，水浮力一般为有利作用。μ1=0时，对于项次4～5(模拟砂土、碎石土)来说，min(cNc/K,fak)=0远小于fak，且抗浮锚杆长度L有限，而ηb较大，按照式(25)或式(27)中min(cNc/K,fak)+γ′L计算的值一般均小于按照式(12)中fak+ηbγ′(b-3)计算的值，对于砂土、碎石土地基承载力的验算，水浮力一般为不利作用。

本文项次4、项次5(模拟砂土、碎石土)的地基承载力特征值250kPa大于项次1～3(模拟黏性土和粉土)的地基承载力特征值150kPa。但是按照本文公式计算，当取μ1=0时，项次4、项次5(模拟砂土、碎石土)的等效地基承载力特征值为160kPa，反而小于项次1～3(模拟黏性土和粉土)的等效地基承载力特征值260kPa，该结果是否符合工程实际情况，需引起重视，仅供设计参考。

4 结论

(1)当裙房作用于基底的压力不小于基底水浮力时：基础埋置深度的地基承载力修正系数ηd为1.0时，地下水位对等效地基承载力特征值的影响不大；ηd大于1.0时，对于等效地基承载力特征值的计算，地下水位为不利因素，且ηd值越高影响越大。

(2)当裙房作用于基底的压力小于基底水浮力时：对于黏性土和粉土地基承载力的验算，水浮力一般为有利因素，从安全角度考虑，建议设计师不考虑此有利因素。对于对砂土、碎石土地基承载力的验算，水浮力一般为不利因素，当按照本文公式验算的地基承载力不满足文献[1]要求时，从安全角度考虑，建议设计师宜根据工程实际情况采取适当的加强措施，例如：加大主楼基础埋深、增加抗浮锚杆长度等。

(3)进行地基承载力验算时应考虑地下水位的影响并宜选择多个不同的地下水位标高进行验算，地基承载力验算最终结果宜综合考虑。