State transformation multi-state constraint Kalman filter for visual-inertial integrated navigation

WANG Maosong, ZHAO Qichao, WU Wenqi, DU Xueyu

(1. College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410073, China; 2. The 91851 Unit of PLA, Huludao 125000, China)

Abstract:A new Kalman filter flow for visual-inertial integrated navigation, which is named as state transformation multi-state constraint Kalman filter (ST-MSCKF) is proposed to improve the accuracy of integrated navigation system. The difference between the standard multi-state constraint Kalman filter (MSCKF) and the ST-MSCKF is that the latter uses rigorous nonlinear velocity error definition. Based on the nonlinear velocity error, the system error model and measurement model of the visual-inertial navigation are reconstructed. As a result, the ST-MSCKF has better covariance consistency than the MSCKF, which leads to higher position and attitude estimation accuracy. Unlike the state-of-the-art observability constrained MSCKF (OC-MSCKF) to solve the inconsistency problem, the ST-MSCKF does not need to modify the state transition matrix and the measurement matrix in real time to maintain the observability of the visual-inertial navigation system, thus the computational cost is saved. The execution process of the ST-MSCKF is exactly the same as the standard MSCKF. Extensive land vehicle experimental results demonstrate that the ST-MSCKF has the same accuracy as OC-MSCKF and higher position and attitude accuracy than the MSCKF, which has good engineering application value.

Key words:ST-MSCKF; visual-inertial integrated navigation; nonlinear velocity error; covariance inconsistency

Visual-inertial odometer (VIO) problem has always been a hot topic in the research community of state estimation for a wide range of applications, especially in GNSS-denied environments[1-6].Among all the approaches, the VIO solution that uses an inertial measurement unit (IMU) and a monocular camera has drawn significant interests, since the small size and low-cost configuration. Monocular camera has the problem of metric scale uncertainty. However, an IMU can provide absolute scale for visual odometer, and can also assist the extraction and matching of visual features. After the loss of visual information, inertial navigation system (INS) can still work for a short time with high accuracy. At the same time, visual odometer can also provide a variety of constraints for inertial navigation. Therefore, inertial navigation and visual odometer have good complementary characteristics[7].

The integrated navigation algorithm of VIO can be generally classified into two categories, one is loosely-coupled integration, the other is tightly-coupled integration. In loosely-coupled integration mode, inertial navigation information and visual information are processed separately. Measurements from IMU are used for state transmission, while the pose of visual calculation is used as updating information of the IMU[8,9]. Generally, this process is realized by using an extended Kalman filter (EKF). However, this method does not fully take IMU’s auxiliary function into vision. Therefore, the drift of IMU state cannot be corrected by visual pose. Different from the loosely-coupled integration, the tightly-coupled integration method utilizes the mutual original information of IMU and vision to realize the state estimation. Thus, better robustness and accuracy can be achieved. The realization of VIO tightly-coupled integration can either use the Kalman filter algorithm[10]or the optimization algorithm[11,12]. The latter is generally considered to be more accurate than the former, since more measurements are used at each iteration cycle. But, the iterative solution of the nonlinear equation requires a lot of computing resources, which is difficult to implement real-time computation on the resource constrained platform. On the contrary, EKF based approach has better computational efficiency, and easy to be implemented on mobiles devices, for example Tango.

However, the early EKF based VIO algorithm has the inconsistency problem. Though the heading angle is not observable in the linearized system model in the multi-state constraint Kalman filter (MSCKF)[13]and also in EKF-simultaneous localization and mapping (SLAM)[14], it appears to be observable. The underlying reason of the inconsistency originates from the way the EKF Jacobians are computed[15]. To solve the inconsistency problem, a lot of variants of EKF are proposed. For example, the first estimate Jacobian EKF (FEJ-EKF)[16], the Robocentric-EKF[17], the observability constrained (OC)-EKF[18,19]. Results have shown that the OC-EKF performs superior state estimation accuracy to FEJ-EKF and Robocentric-EKF both theoretically and experimentally. The difficulty when using the OCEKF is that a deep study of the unobservability subspace of the system over different scenarios need to be done first. However, in practical application, it is difficult to analyze the overall observability of the system from both static and dynamic aspects. Sometimes, the observability in the static base is different in the dynamic base. The question is that whether a Kalman filter method exists that is simpler and easier to be implemented than the OCEKF in real applications and also the observability of the system does not need to be known beforehand? The answer is yes.

Recently, the invariant-EKF (IEKF) methodology with the rigid body motion represented by matrix lie group has become the popular means to solve the inconsistency problem[20,21], and followed by researchers to solve the covariance inconsistency problem in VIO[22-24], and even in Artificial Intelligence (AI) aided land vehicle application[25]. The merit of IEKF is that unlike OCEKF, IEKF does not need to know the observability of the system in advance. However, the derivation and implementation processes of IEKF are complicated.

In this paper, we still focus on the VIO covariance inconsistency problem of MSCKF. A novel version MSCKF with robust covariance consistency is developed, which is named as state transformation-MSCKF (ST-MSCKF). The basic idea of the state transformation is consistent with our recent work of INS/global navigation satellite system(GNSS)based loosely-coupled integration[26],INS/GNSS tightly-coupled integration[27]and INS/Odometer integration[28].

1 System model of the state transformation multi-state constraint Kalman filter

The MSCKF algorithm was first proposed in Ref.[13]. The drawback of MSCKF is that it faces the inconsistency problem. The inconsistency here means that the filter gains spurious information along directions of the state space where no information is available. For example, the heading angle is not observable in the VIO system.However, the covariance of the estimated heading error still has a reduction with time, which results in the wrongly estimated heading angle and even the position. Though the inconsistency problem has been investigated extensively[15-19], it has not been fully solved.

This paper does not serve as a “therapeutic drug” to cure the inconsistency problem in VIO like Ref.[15-19], but works as a “preventive medicine” to prevent the inconsistency problem. The excellent consistency performance of the ST-MSCKF owes to the nonlinear velocity error definition. The system model of the ST-MSCKF is illustrated in detail in this section. Several coordinate frames are defined first.

World reference coordinate frameW: this coordinate frame is the local tangent plane coordinate frame, which is fixed with the earth. In order to meet the seamless operation of the algorithm, the position and attitude of IMU and camera, as well as the feature points in the scene are represented inWframe.

Vehicle body coordinate frameM: this coordinate frame is fixed with the vehicle body, the origin is located at the vehicle center of mass, and the direction of the coordinate axis is the Front-Right-Down (FRD).

IMU coordinate frameI: this coordinate frame takes the center of the three accelerometers as the origin. The three directions meet the FRD.

Camera coordinate frameC: this coordinate frame is fixedly connected with the camera. The origin of the coordinate frame is at the optical center of the camera. The x-axis and y-axis are parallel to the imaging plane. The x-axis is transverse, the y-axis is longitudinal, and the z-axis is parallel to the lens axis.

Earth centered earth fixed coordinate frameE: this coordinate frame is fixed with the earth, the origin of it is located at the center of the earth, the x-axis points to the intersection point of the equator and the reference meridian, the z-axis points to the north pole along the earth's rotation axis, and the y-axis is determined by the right-hand rule.

In the traditional VIO, the position of feature points is usually added to the state vector, and the poses of the platform are continuously optimized through new observation until the feature points disappear. However, in the MSCKF algorithm, the state vector no longer contains the position of feature points, but replaced with the camera pose at the past time. The state vector is in the form of a sliding window, adding new camera positions and discarding the old ones.

The state vector of the filter at timetis composed of IMU related quantity and camera related quantity

wherexis the whole state vector,xSTIMU-is IMU related state, andxSTC-is camera related state. ThexSTIMU-is defined as follows[15]

whereis Hamilton quaternion, which represents the rotation fromIframe to W frame,andare the velocity and position of the vehicle resolved in W frame, respectively;bgandbaare the biases of gyros and accelerometers, respectively;represents the rotation fromCframe toIframe,is the position vector fromIframe toCframe resolved inIframe.

In the Kalman filter process, the errors of the states are usually used. The IMU related error states can be written from Eq.(2).

where the quantities in Eq.(3) represent misalignment angle vector of attitude, velocity error vector, position error vector, gyro bias error vector, accelerometer bias error vector, installation angle error between IMU and camera, lever-arm error between IMU and camera, respectively.

It should be emphasized here that the traditional definition of velocity error useswhereis the estimated velocity, andis the true velocity. However, this velocity error definition does not follow the coordinate frame consistency strictly[27,28]. Therefore, a rigorous velocity error definition in this paper is given by

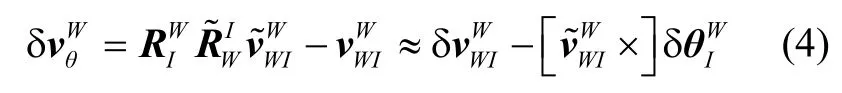
whererepresents the rotation matrix fromIframe to W frame,represents the estimated rotation matrix fromWframe toIframe,is the new nonlinear velocity definition.

The system error model of IMU related error states can be written as

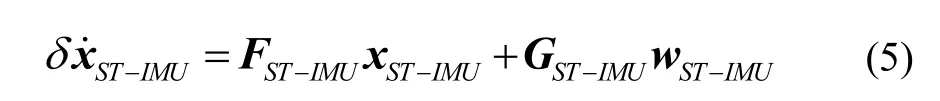
whereFST-IMUis system matrix, which is given by

whereΩWis the projection of the earth’s angular velocity inWframe and I3is a 3 by 3 identity matrix.is the gravity vector inWframe, which can be obtained from Eq.(7).

In Eq.(7),is the rotation matrix fromEframe toWframe, which is written as

The symbolsLWandλWrepresent the latitude and longitude of the origin ofWframe, respectively. The gravity vectorin Eq.(7) is the function of position, and

wherehWis the height above the ellipsoid of the origin ofWframe,REis the transverse radii of curvature, andeis the eccentricity of the ellipsoid.

It can be seen clearly that there is no specific force term in Eq.(6) any more. The specific force term has been replaced byFor local navigation problem, the new system matrixFST-IMUis more robust than that of traditional EKF[13], sinceis nearly constant. Therefore, the covariance consistency is guaranteed.

However, for high accuracy VIO applications, these two terms cannot be omitted.

GST-IMUis noise shaping matrix, which is given by

The system noise can be represented as Ref.[15]

wherewgandwaare the measurement white noise vectors of the gyros and accelerometers, respectively;wwgandwwaare the driven white noises of the random walk processes of the gyro constant biases and accelerometer constant biases, respectively;wθandwpare relative attitude angle noises and relative displacement noises, respectively.

In the ST-MSCKF algorithm, the state vector contains the camera pose of the pastNframes.Ndepends on the length of the currently tracked feature points and the maximum width of the window. At timet, the state vector associated with the camera is expressed as follows

whererepresents the rotation fromWframe toCframe,represents the camera position resolved inWframe. The error vector of Eq.(13) can be written as

The relationship between camera attitude angle error and quaternion, as well as the relationship between camera attitude angle error and rotation matrix are as follows

The state and covariance matrix are propagated when a new IMU measurement value is obtained, while after each acquisition of camera measurement value of key frame, a new camera pose state is added to the state vector, and the state covariance matrix is augmented.

In state augmentation, the new camera error state can be expressed as

The augmented covariance matrix can be represented as

wherePkandare the covariance matrices before and after the augmentation, respectively. I6N+15is a 6N+15 dimensional identity matrix. And

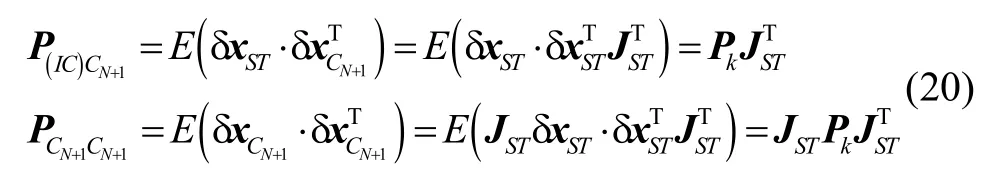
2 Measurement model of state transformation multi-state constraint Kalman filter

In the ST-MSCKF algorithm based visual-inertial integrated navigation, IMU information is used for state propagation, visual information is used as observations. The basic measurement model is feature point reprojection error.

Suppose that in a series of feature points, thej-th feature pointfjis included in thei-frame image. The three dimensional position of the feature point in camera frame is, while the two dimensional position in image plane is. They have the relationship that

The reprojection error of the feature point is

and

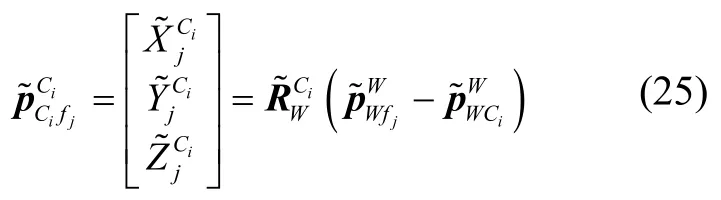
where the positionof the feature point can be estimated by nonlinear optimization process to minimize the reprojection error, which utilizes bundle adjustment and inverse depth parameterization.

The reprojection erroris related to the camera pose and the position of the feature points. Since the position of the feature point is not included in the state vector, it cannot be expressed linearly by the system error state. In order to solve this problem, firstly, it is represented by system error state and feature point position error

Assume that the feature pointfjis included inMjframe images, then the reprojection errors in all these images are stacked into a column.

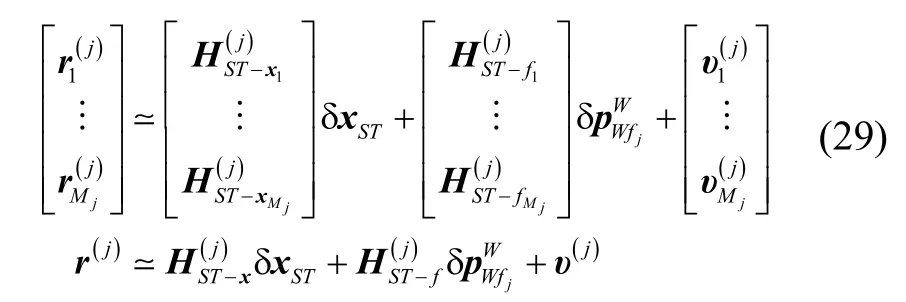
SupposeAis a unitary matrix, and the columns ofAform a set of bases of left null space. Multiply the above formula byATto the left

In the above formula, the right side of the equation does not contain the position of feature points, so the observation equation in Kalman filter is satisfied. And the reprojection error after transformationcan be used for Kalman filter observation and updating.

3 Experimental results

This section evaluates the proposed ST-MSCKF algorithm by using three sets real-world experiments. The performance of three filters are compared: (1) the standard MSCKF[13], (2) OC-MSCKF[19], (3) the proposed ST-MSCKF.

3.1 First experiment: KITTI datasets

The open source data KITTI Vision Benchmark Suite[29]has raw camera images, IMU measurements and GPS/IMU reference results for evaluating the algorithms. The cameras and GPS/IMU results are manually synchronized, with sampling rates of 10 Hz and 100 Hz, respectively. The source data used in this paper are the un-synchronized IMU measurements sampling at 100 Hz and the rectified grayscale image sequences from left camera sampling at 10 Hz. The ground truth is taken from the GPS/IMU integrated solution. The resolution of stereo images is 1226 × 370 pixels, with 90 ° field of view.

For feature detection, the FAST detector[30]is used for detecting corner features in the image. The major advantage of the FAST algorithm is its high efficiency in reaching accurate corner localization in an image. For feature tracking, the Kanade Lucas Tomasi (KLT) tracker[31]is used. The advantage of KLT tracker is that it allows tracking features over long image sequences and undergoing larger changes by applying an affine-distortion model to each feature.

Sequences “2011_10_03_drive_0034” , “2011_10_03_drive_0042” , “2011_09_30_drive_0018” , “2011_09_30_drive_0028”, “2011_09_30_drive_0033” are chosen, which are labeled as 1, 2, 3, 4, 5, respectively. The algorithms are evaluated by setting the same Kalman filter initials.

Results of two sequences “4” and “5” are shown in details in the figures 1-4, while the statistical results of all sequences are displayed in Tab.1 and Tab.2.

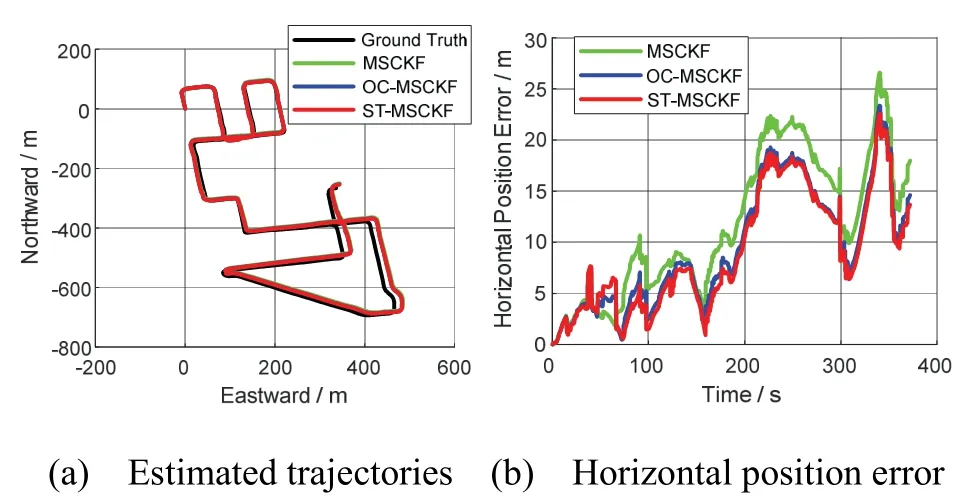
Fig.1 The results of trajectory estimation in sequence 2011_09_30_drive_0028 and horizontal position error

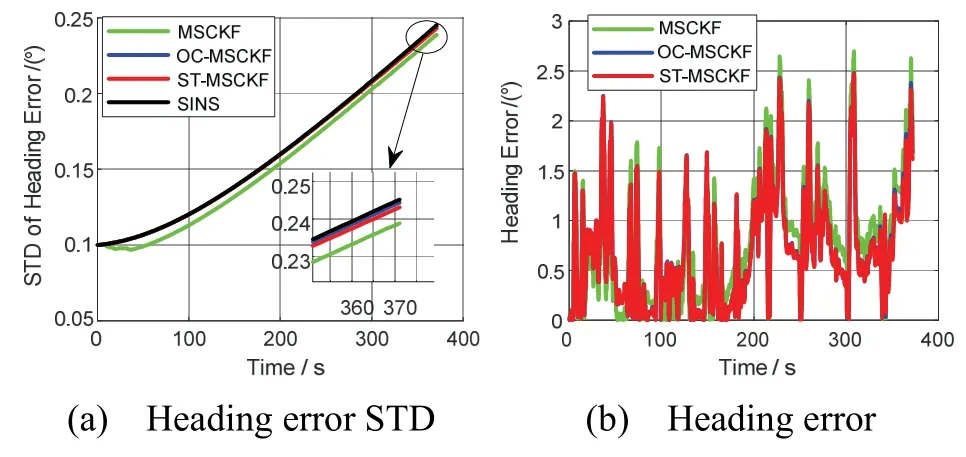
Fig.2 The results of heading error STD in sequence 2011_09_30_drive_0028 and heading error

It is shown in Fig.1(b) and Fig.3(b) that ST-MSCKF has higher horizontal positioning accuracy than the standard MSCKF. But, OC-MSCKF does not always perform superior positioning accuracy to the MSCKF, which can be seen in Fig.3(b). The reason is that some precision is lost when modifying the system matrix and measurement matrix by using the OC-MSCKF[18]. However, the system matrix of the ST-MSCKF is derived rigorously based on the transformed velocity error. Therefore, the precision is maintained.

Fig.3 The results of trajectory estimation in sequence 2011_09_30_drive_0033 and horizontal position error

As illustrated in Fig.2(a) and Fig.4(a), both OC-MSCKF and ST-MSCKF have better heading error standard deviation (STD) consistency of the Kalman filter than that of the standard MSCKF. Though the heading angle is not observable[18], the heading error STD of MSCKF has a gradually decreasing tread. As a result, both OC-MSCKF and ST-MSCKF have superior heading accuracy to MSCKF which can be seen from Fig.2(b) and Fig.4(b). Note that the heading error lines of OC-MSCKF and ST-MSCKF are overlapped.

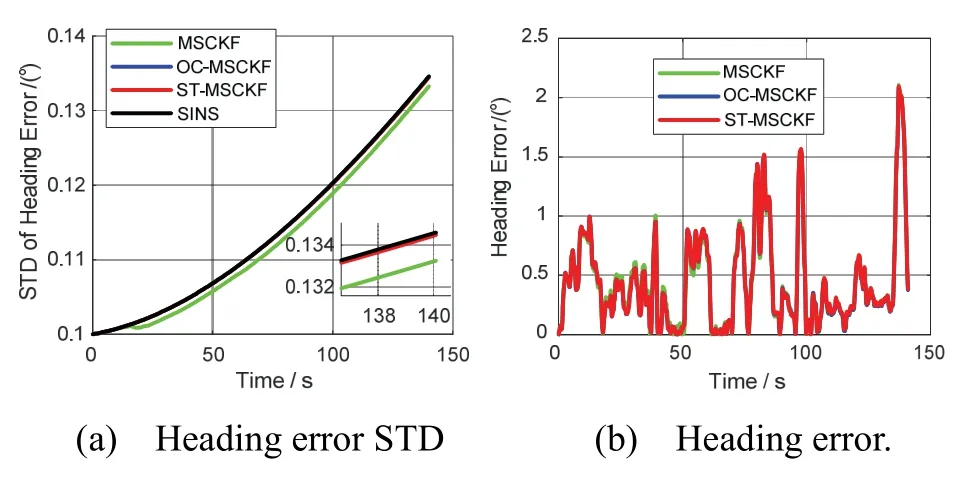
Fig.4 The results of heading error STD in sequence 2011_09_30_drive_0033 and heading error

The statistical horizontal position root-mean-square -error (RMSE) in Tab.1 and heading RMSE in Tab.2 of all sequences have shown the superior positioning and heading accuracy of the proposed ST-MSCKF to state of the art OC-MSCKF.

Tab.1 Horizontal position RMSE of KITTI data in meters

Tab.2 Heading RMSE of KITTI data in degrees

3.2 Second experiment: land vehicle field test

This section conducts our own land vehicle field test to validate the performance of the proposed algorithm. The sensor configurations of the test are shown in Fig.5.

Fig.5 Sensor configurations of the land vehicle field test

The sensors are mounted on the top of the vehicle, which include a GNSS receiver with frequency 10 Hz, a monocular camera with frame rate 20 Hz and a Stim300-IMU with sampling frequency 200 Hz. All the sensors are well synchronized. Single point positioning and velocity accuracy of the GNSS receiver are 10 m and 0.1 m/s, respectively. The monocular camera has a resolution of 1620×1220 pixels, and the specifications of the Stim300-IMU are displayed in Tab.3.

Tab.3 III Specifications of the stim300-IMU

The experimental trajectory is displayed in Fig.6 with length 4.5 km. Experimental results are shown in Fig.7, Fig.8 and Tab.4. The ground truth of the test is generated from GNSS/SINS integration with fixed point smoothing algorithm.

Fig.6 Trajectory of the land vehicle field test

The estimated trajectories of all algorithms of the test are illustrated in Fig.7(a), while Fig.7(b) displays the horizontal position errors of the three algorithms under the same Kalman filter initial conditions. As shown in Fig.7(b), both OC-MSCKF and ST-MSCKF have higher positioning accuracy than the standard MSCKF, especially when after 588 s. As can be seen from Fig.8(a), both OC-MSCKF and ST-MSCKF have better heading error STD consistency than the MSCKF. As a result, the heading accuracy of OC-MSCKF and ST-MSCKF are higher than that of MSCKF, which can be seen in Fig.8(b). The statistical horizontal position RMSE and heading RMSE of the three algorithms are illustrated in Tab.4.

Fig.7 Estimated trajectories and horizontal position error in land vehicle test

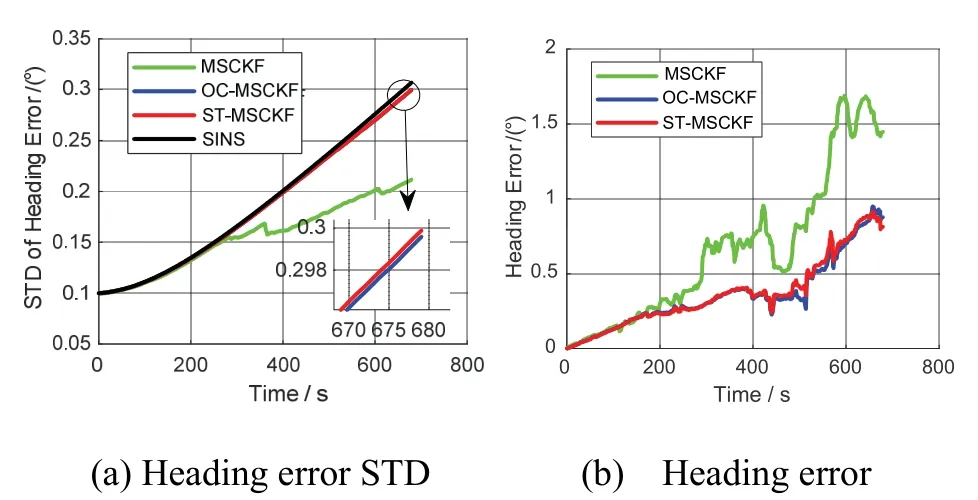
Fig.8 Heading error STD and heading error of the land vehicle test

Tab.4 Horizontal position RMSE and heading RMSE of the land vehicle field test

4 Conclusion and Future Work

In this paper, a state transformation multi-state constraint Kalman filter (ST-MSCKF) is proposed to solve the inconsistency problem of VIO system. The performance of the proposed algorithm has been validated by extensive real-world experiments.Compared with the state-of-the-art algorithms to solve the inconsistency of VIO, the proposed algorithm has the following advantages,

1)The transformed velocity error of the ST-MSCKF is more rigorous than the general linear velocity error definition, and the physical meaning is clearer.

2)The system matrix of the ST-MSCKF based VIO integrated navigation system has no specific force term any more, but replaced by gravity vector term. Therefore, the Kalman filter is more robust and has better consistency especially in dynamic environments.

3)Compared with OC-MSCKF, the proposed ST-MSCKF is easy to implement since it does not need to have a deep study of observability of the integrated navigation system beforehand.

4)The ST-MSCKF does not need to modify the system matrix and measurement matrix as OC-MSCKF which needs to enforce the observability of the integrated navigation system in real time.

The proposed algorithm has strong engineering application flexibility and applicability. For example, it can be further applied to binocular VIO system and has the flexibility to add wheel odometer or GNSS measurements into the Kalman filter flow.