同构函数在解决高考压轴题中的应用
张春华
(山东省东营市第一中学 257091)
如何去构造一个同构函数,常用的同构函数形式又有哪些?本文试图通过以双变量和指对混合两类问题的分析,探索如何构造同构函数,以提高学生解题能力,掌握高考数学中解决函数压轴题的一种途径.
一、双变量地位等同问题
2020年的高考可以看出,新高考注重了数学素养的考查,尤其是创新思维.这种题型一般含有两个变量,通过变形整理可将两个变量分别移到不等式或等式两侧,构造出同一个函数取两个不同变量时的函数值大小问题,进而转化为函数单调性问题.这种双变量问题在高考题中频繁出现,下面举例分析.
例1(2020全国高考二卷理科数学11题)若2x-2y<3-x-3-y,则( ).
A.ln(y-x+1)>0 B.ln(y-x+1)<0
C.ln|x-y|>0 D.ln|x-y|<0
解析将不等式移项变形为2x-2y<3-x-3-y,构造函数f(t)=2t-3-t,由其为单调递增函数知x 例2(2020全国一卷理科数学12题)若2a+log2a=4b+2log4b,则( ). A.a>2bB.a<2b C.a>b2D.a 解析条件等式两边结构类似,构造函数f(x)=2x+log2x,则f(x)为增函数,由选项可知只需要比较f(a)和f(2b),f(a)和f(b2)大小即可. 而f(a)-f(b2)=22b-2b2-log2b,b取不同值结果不同,因此选B. 例3(2010高考辽宁卷理科数学21题)已知函数f(x)=(a+1)lnx+ax2+1 (1)讨论函数f(x)的单调性; (2)设a<-1,如果对任意x1,x2∈(0,+∞),|f(x1)-f(x2)≥4|x1-x2|,求a的取值范围. 解析(1)略; (2)所证不等式|f(x1)-f(x2)|≥4|x1-x2|含绝对值,所以由(1)问可知,当a≤-2时,f(x)单调递减,故只需要知道x1,x2的大小即可去掉绝对值.不妨设x2>x1,所证不等式去掉绝对值后为f(x2)-f(x1)≥4x2-4x1, 即f(x2)-4x2≥f(x1)-4x1,发现不等式两侧为关于x1,x2的同构式,故可以将同构式构造成函数g(x)=f(x)+4x,将问题转化为g(x)=f(x)+4x单调递减求参数a的范围问题. 在解决指数函数与对数函数的混合不等式恒成立求参数范围或证明指对不等式时,如果使用参变分离、隐零点代换等方法,都避免不了复杂计算,有时效果也不一定好,而使用同构法会达到意想不到的效果. 如何构造同构函数呢?一般情况下含ex和lnx的函数,主要是统一化为左边或化为右边构造同构式.同构式需要构造这样一个母函数,这个函数既能满足指数与对数互化,又能满足单调性和最值易求等特点,因此常见的同构形式大多为y=xlnx,y=xex,或其同族函数.经过同构变形,再结合复合函数的单调性,可以快速解决证明不等式、恒成立求参数的取值范围等问题. 构造同构函数通常有三种基本模式: (1)积型 (2)商型 (3)和差型 其中x=elnx=lnex在变形构造同构式中起着重要作用. 例4 (2018高考全国一卷文科数学21题)已知函数f(x)=aex-lnx-1. (1)设x=2是f(x)的极值点,求a,并求f(x)的单调区间; 解析(1)略; (1)求a,b; (2)证明:f(x)>1. 解析(1)a=1;b=2,详细解答略. (2)本题如果直接求导,将非常复杂,不妨采用同构函数的方法. 综上,通过双变量和指对混合两类高考真题的分析,我们发现同构式思想对于解决这两类问题有规律可循,而且平时各类模拟试题中屡见不鲜,只要大胆尝试,把握其中的规律,解决这类问题堪称秒杀!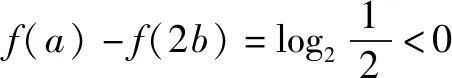
二、指对混合问题