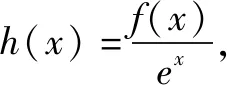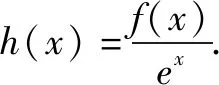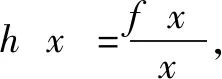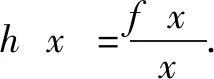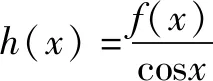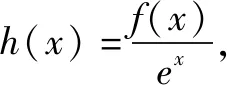例谈构造函数解一类导数题

李 俊

(云南省玉溪市江川区第一中学 652600)

近几年各地高考数学试卷中，许多涉及函数选择题或填空题的题目，可采用构造函数法进行解答.所谓构造函数法是指通过一定方式，设计并构造一个与有待解答问题相关的函数，通过观察分析，借助函数本身的性质，如单调性或利用运算结果，解决原问题的方法.简而言之就是构造函数解答问题.如何合理地构造函数就成为了问题的关键，这里我们就这方面问题探讨一下.

例1已知函数f(x)的定义域为R，f(-1)=2，且对任意x∈R，都有f′(x)>2，则f(x)>2x+4的解集为( ).

A.(-1,1) B.(-1，+∞)

C.(-∞，-1) D.(-∞，+∞)

解析构造函数h(x)=f(x)-2x-4，所以h′(x)=f′(x)-2，由于对任意x∈R，f′(x)>2，所以h′(x)=f′(x)-2>0恒成立，所以h(x)=f(x)-2x-4是R上的增函数，又由于h(-1)=f(-1)-2×(-1)-4=0，所以h(x)=f(x)-2x-4>0，即f(x)>2x+4的解集为(-1，+∞)，故选B.

点评对于f′(x)>a(a≠0)，可构造函数h(x)=f(x)-ax.

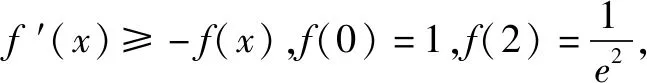
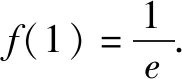
点评对于f′(x)+f(x)>0，可构造函数h(x)=exf(x).

例3已知f(x)>0为f(x)<0上的可导函数，且f(x)>x，均有f(x)

A.e2016f(-2016)e2016f(0)

B.e2016f(-2016)

C.e2016f(-2016)>f(0)，f(2016)>e2016f(0)

D.e2016f(-2016)>f(0)，f(2016)

例4若函数y=f(x)在R上可导且满足不等式xf′(x)+f(x)>0恒成立，对任意正数a、b，若a

A.af(b)

C.af(a)

解析由已知xf′(x)+f(x)>0可构造函数h(x)=xf(x)，则h′(x)=xf′(x)+f(x)>0，从而h(x)在R上为增函数.因为a

点评对于xf′(x)+f(x)>0，可构造函数h(x)=xf(x).

例5已知f(x)是定义在(0，+∞)上的非负可导函数，且满足xf′(x)-f(x)≤0，对任意正数a、b，若a

A.af(b)≤bf(a) B.bf(a)≤af(b)

C.af(a)≤bf(b) D.bf(b)≤af(a)

故选A.

例6设函数f(x)在R上的导函数为f′(x)，且2f(x)+xf′(x)>x2，下面不等式恒成立的是( ).

A.f(x)>0 B.f(x)<0 C.f(x)>xD.f(x)

解析由已知，首先令x=0得f(x)，排除B，D.

令h(x)=x2f(x)，则h′(x)=x[2f(x)+xf′(x)]

综上f(x)>0,故选A.

点评对于xf′(x)+nf(x)≥0，可构造函数h(x)=xnf(x).

例7设函数f(x)是(0,+∞)上的非负可导函数，且xf′(x)-2f(x)>0，下列不等式成立的是( ).

例8设f(x)、g(x)是R上的可导函数，f′(x)、g′(x)分别为f(x)、g(x)的导函数，且满足f′(x)g(x)+f(x)g′(x)<0，则当a

A.f(x)g(b)>f(b)g(x) B.f(x)g(a)>f(a)g(x)

C.f(x)g(x)>f(b)g(b) D.f(x)g(x)>f(b)g(a)

解析构造函数h(x)=f(x)g(x)，则h′(x)=f′(x)g(x)+f(x)g′(x)<0，所以函数h(x)=f(x)g(x)在R上为减函数，因为xf(b)g(b)，故选C.

点评对于f′(x)g(x)+f(x)g′(x)>0，构造函数h(x)=f(x)g(x).

例9设函数f(x),g(x)在[a,b]上均可导,且f′(x)

A.f(x)>g(x) B.f(x)

C.f(x)+g(a)

解析构造函数h(x)=f(x)-g(x)，则h′(x)=f′(x)-g′(x)<0，所以函数h(x)=f(x)-g(x)在[a,b]上为减函数，因为af(x)-g(x)，故f(x)+g(a)

点评对于f′(x)-g′(x)>0或f′(x)+g′(x)>0，构造函数h(x)=f(x)-g(x)或h(x)=f(x)+g(x).

在平时的教学中，我们要勤于积累，善于总结，熟练掌握导数四则运算，通过对题目的分析，根据题目的不同形式在解题中合理巧妙地构造函数，结合导数这一工具进行合理计算，使复杂的问题转化成熟悉而简单的问题，进而找到问题解决的突破口!

模型总结关系式为“加”型

(1)f′(x)+f(x)≥0,构造h(x)=exf(x)，则h′(x)=[exf(x)]′=ex[f′(x)+f(x)].

(2)xf′(x)+f(x)≥0,构造h(x)=xf(x)，则h′(x)=[xf(x)]′=xf′(x)+f(x).

(3)xf′(x)+nf(x)≥0,构造h(x)=xnf(x)，则h′(x)=[xnf(x)]′=xnf′(x)+nxn-1f(x)=xn-1[xf′(x)+nf(x)].

关系式为“减”型