高中数学中立体几何试题的有效解题方法探究

葛宏伟

(内蒙古自治区乌海市第十中学 016000)

立体几何知识需要学生从多角度考虑，对学生各方面的能力提出了很高的要求.教师在教学中要对学生进行“授之以渔”的教育，从方法上引导学生，促进学生积极思考.教师要引导学生在夯实基本功的基础上探究解题方法，总结解题规律，深化认识.只有学生具有了较好的基础知识和敏锐的洞察力，通过认真揣摩和分析的方式才能够明确各个数量之间的关系，构建出空间图形.通过想象和探究的方式来确定立体空间观念，构建出空间模型，探究解题思路.

一、射影法

在立体几何中线面角和二面角都是非常重要的概念，对于学生解决立体几何问题非常关键.例如如图，P-ABCD是四棱锥，△PAD是等腰直角三角形，AD是它的斜边，其中BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点.

(1)证明：CE∥平面PAB；

(2)求直线CE与平面PBC所成角的正弦值.

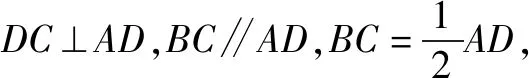
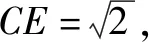
二、最值法

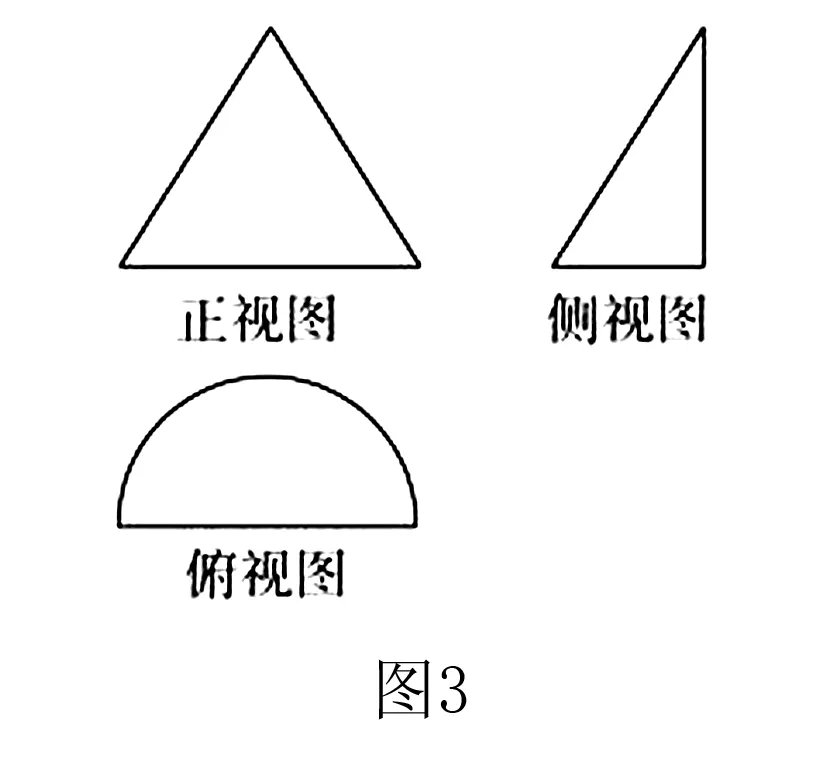
最值法是解决立体几何的一种常见方法，通常用于解决最大值与最小值方面的问题.例如如图所示的三视图，正视图中的三角形边长为2，侧视图的半圆半径为1，求内接三棱锥的体积的最大值是( ).

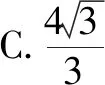
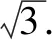
三、辅助线法

通过恰当应用辅助线可以把看似毫无关系的空间数量联系起来，在辅助线的帮助下快速推理，准确迁移，实现对试题的解答.例如如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则( ).

A.BM=EN，且直线BM，EN是相交直线

B.BM≠EN，且直线BM，EN是相交直线

C.BM=EN，且直线BM，EN是异面直线

D.BM≠EN，且直线BM，EN是异面直线

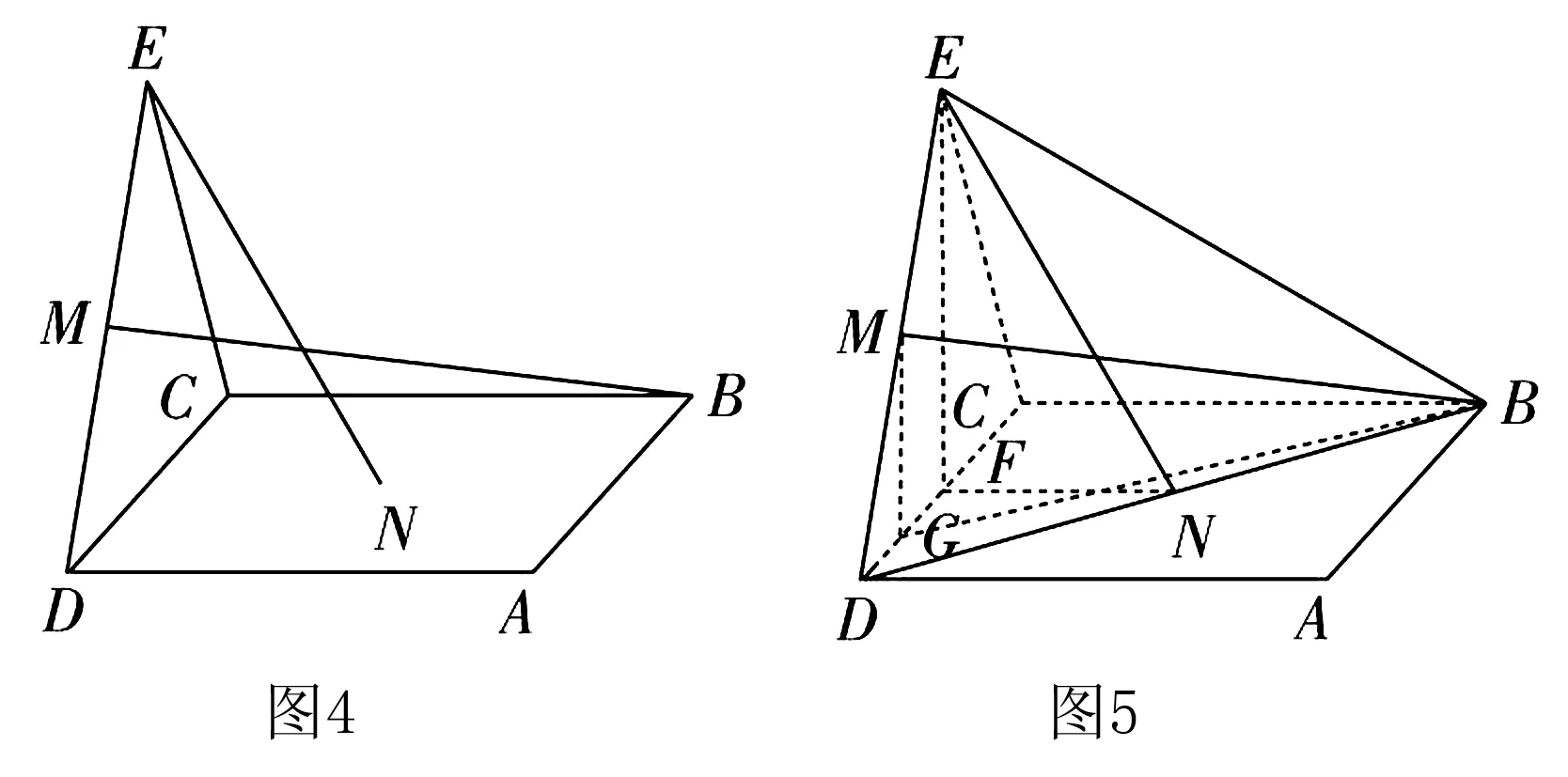
思考中，学生会做出辅助线，呈现如图2所示的图形.通过推理和逻辑分析，可以证明∴EF⊥平面ABCD.

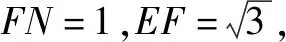
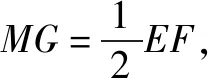
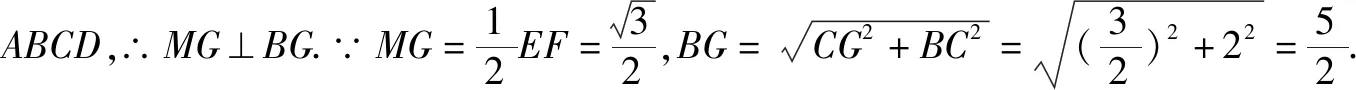
四、空间向量法

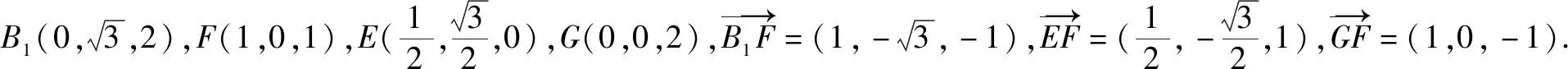
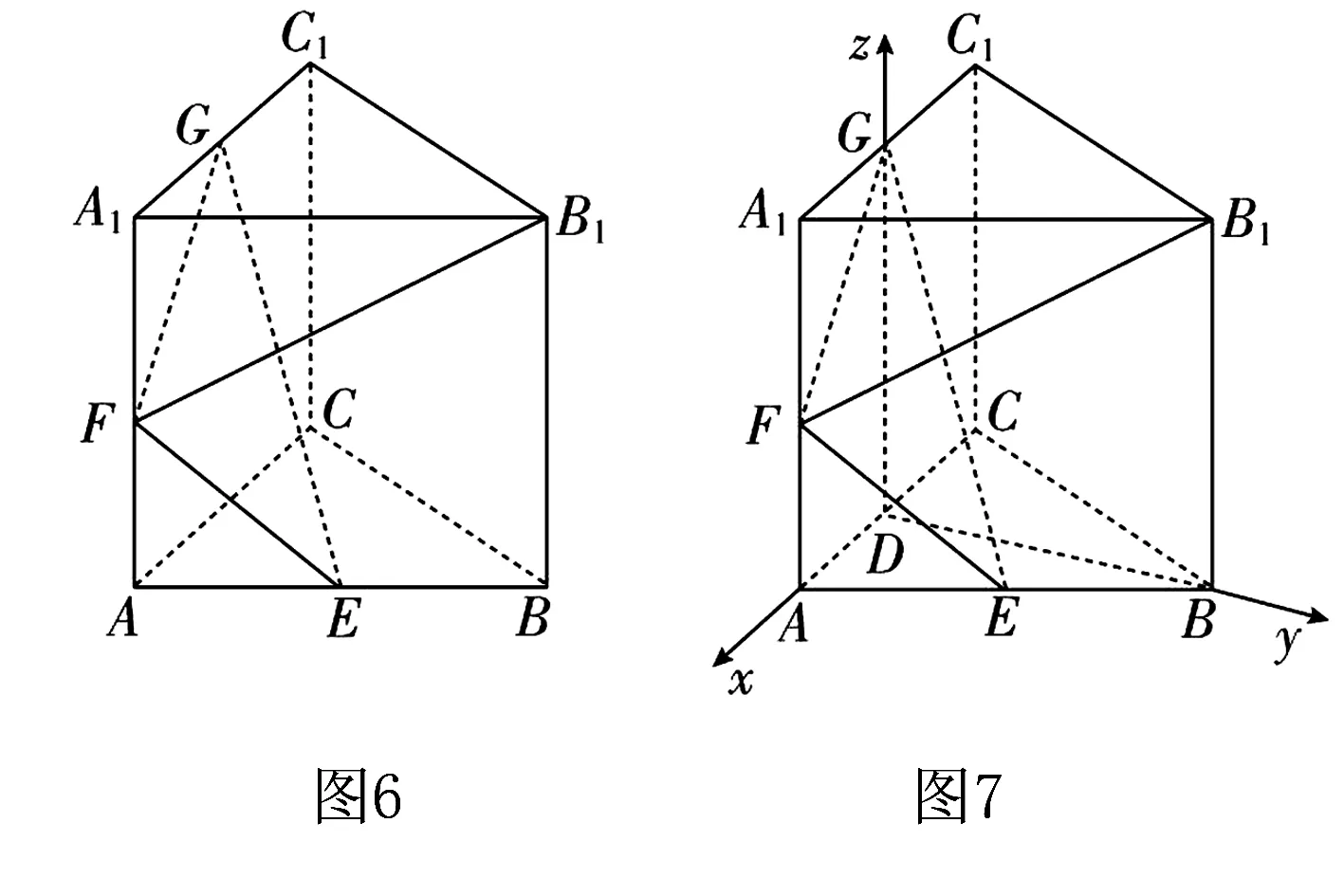
总之，“授之以鱼”不如“授之以渔”，学生掌握了不同的解题方法和解题策略，会形成对知识的清楚认识.学生主动探究会习得解题方法和策略，带着对知识的理性理解来思考和分析.教师科学地指导学生，鼓励学生在大脑中建构图形的立体框架和结构，把握各个数量关系，会促进学生更好地理解知识，提高解题能力.