编程思维与物理思维完美融合的解题技巧

昌明彦

(贵州省思南中学 565100)

所谓“编程思维(computational thinking)”就是“理解问题——找出路径”的思维过程，它由分解、模式识别、抽象、算法四个步骤组成，如图1所示.解答物理试题一般也包含四个步骤，即确定研究对象；受力和运动分析(建立模型)；运用概念、规律、定理和公式等列方程；解方程和验证结果是否符合题意.以2020年全国卷Ⅲ第25题为例阐述编程思维在物理试题中分析、解答的应用技巧.

图1

真题呈现如图2，相距L=11.5m的两平台位于同一水平面内，二者之间用传送带相接.传送带向右匀速运动，其速度的大小v可以由驱动系统根据需要设定.质量m=10kg的载物箱(可视为质点)，以初速度v0=5.0m/s自左侧平台滑上传送带.载物箱与传送带间的动摩擦因数μ=0.10，重力加速度取g=10 m/s2.

图2

(1)若v=4.0m/s，求载物箱通过传送带所需的时间；

(2)求载物箱到达右侧平台时所能达到的最大速度和最小速度；

思维分析根据题意可知载物箱以恒定速度v0在传送带上从左向右运动，采用编程思维分析如图3:

图3

经过上述四步分析，可知载物箱的质量m=10kg和初速度v0=5.0m/s，传送带的长度L=11.5m，载物箱与传送带之间的动摩擦因数μ=0.10在(1)、(2)、(3)问中均保持不变的.而传送带的速度在每一问中均不相同，这是解答本题的关键点.

关键能力本题的关键能力为理解能力、模型建构能力和推理能力，能用传送带模型，通过对载物箱的受力分析，得出运动情况，再运用牛顿运动定律、动能定理和冲量、动量定理解答.

解题思路(1)传送带的速度v=4.0m/s小于载物箱速度v0=5.0m/s，可得载物箱先做匀减速运动，在水平方向只受动摩擦力.

由牛顿第二定律:

μmg=ma

①

设载物箱速度减小到与传送带速度相等时位移为x1，由运动学公式：

②

联立①②式得x1=4.5m

③

x1=4.5m小于L=11.5m，当载物箱速度与传送带速度相等后，做匀速运动

v=v0-at1

④

⑤

联立①③④⑤式得t=2.75s

阅卷过程中，发现部分学生将①写成a=μg,这个不是牛顿第二定律原始表达式.

(2)要让载物箱达到最大速度，载物箱必需一直做加速运动，设定传送带的速度一直比载物箱速度还要大即可.

最大速度：根据动能定理

⑦

要让载物箱达到最小速度，载物箱必需一直做减速运动，设定传送带的速度一直比载物箱速度还要小即可.

最小速度：根据动能定理

⑧

代入数据得：

此问还可以用牛顿第二定律和运动学公式进行解答，也可以用运动学公式和动量定理解答.

阅卷过程中，针对该问，还发现部分学生对载物箱在传送带上运动进行讨论判断运动情况，问题出在没有理解“传送带的速度大小v可以由驱动系统根据需要设定”这句话的意义.

同时，还发现部分学生对该问是这样解答的.

错误一 ：

最大速度：根据动能定理

最小速度：根据动能定理

错误二：

最大速度：根据动能定理

F=μmg

最小速度：根据动能定理

F=μmg

从物理知识角度来看，好像没有问题，但是阅卷教师给的是0分.有些同学会问，为什么呢？

如果再认真审题发现字母v已经用来表示传送带的速度了，故载物箱到达右侧平台时所能达到的最大速度和最小速度不能用字母v来表示了.载物箱在传送带上从左向右运动的位移在题干中是用字母L表示的，在书写物理公式时要有所指，不能套用课本书上的原始公式.在编程过程中，如果同一个字母或单词表示几个对象，在程序调试的过程中将会出错，或者只运行最后一个.如果学生体验过编程环节，对于该题就不会犯这种错误.

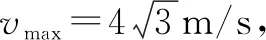
根据编程思维，把复杂的问题分解——化繁为简，其实在解决多物体多过程试题时，一般将全过程进行分解，分析每个物体每个过程的规律；抽象理解——聚焦关键，物理试题来源于生活，一般将研究对象从环境中分离出来，建立理想化模型；模式识别—整合规律，每个研究对象在各阶段的运动和受力情况，满足哪些规律、定律和定理.

近期教育部回答政协提案中讲到，将编程教育纳入到中小学相关课程中.如果学生掌握了编程思维，物理教学将达到事半功倍的效果.