平均差的新公式

谢 翰

(广东省汕尾市陆丰市龙山中学 516500)

统计中最基本的是对一组数据的概括性度量，集中趋势(算术平均数、中位数)与离散程度(平均差、标准差)作为描述数据分布特征的一体两面 , 反映了一组数据的中心值和各数据远离其中心值的程度.只考虑集中趋势会使我们作出对总体的片面判断，只有把集中趋势和离散程度结合在一起分析，才能概括出总体的实际状态.

离散程度指标主要有平均差和标准差两种，平均差(mean deviation)是各数据到其算术平均数的平均距离，它综合反映了各单位相对其算术平均数的平均波动程度.

平均差的含义明确，计算方法简单明了，它能够充分、客观地反映离散程度.但也要看到，它是以离差的绝对值为计算基础的，这就不利于进一步进行代数运算了.所以很多教科书都认为考察离散程度的大小最常用的统计量是标准差而非平均差.很多教科书指出，平均差不是变量的解析函数，也没有函数的可导性，因而在代数推断和应用方面都受到很大限制，并在实际使用上被标准差所取代.据此，本文从离差和平均数的性质重新出发，推导出了不含绝对值的平均差新公式.

因为各单位值与其算术平均数离差之和等于零，即

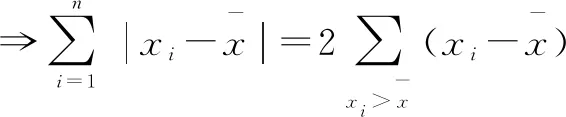
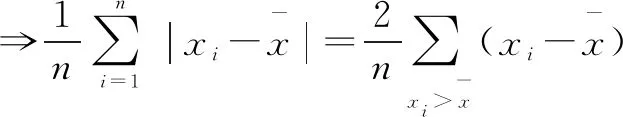
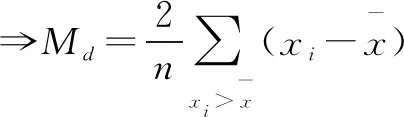
(1)

我们将公式(1)称为新的平均差计量公式，它是由离差和平均数的性质推导出来的，运用公式(1)计算所得的平均差，不仅在数值上与传统方法计算出来的平均差等价，而且拥有很多优良的特性.

从计算方式、数学关系和敏感性等几个方面对平均差与标准差进行比较，可以得出以下结论：

第一，对于谁计算更简便的问题，在数字计算时，平均差计算不存在平方和开平方计算，计算量远低于标准差.在进行代数运算时，有了不含绝对值的平均差新公式，平均差计算更简便的观点在算术领域和在代数领域都能成立.平均差新公式在数学处理上比标准差更为合理和优越.

第二，对于同一组统计数据，平均差(Md)与标准差(σ)一定是如下关系：

σ≥Md≥0

第三，标准差的计算过程中，在离差的绝对值大于1时有高估离散程度问题，在离差的绝对值小于1时有低估离散程度问题.这种现象，在U形分布中比在钟形分布中更为明显.

第四，平均差新公式大大拓展了平均差具有的数学性质，并且与标准差相比，它兼具反映离散程度的准确性优势.从测量离差的普遍思路出发，标准差只是平均差的代替；在不必使用绝对值的平均差新计算方法的情况下，更能代表平均偏离本真的平均差优于标准差，应当大力推广使用和普及.

除此之外，简化后的标准差公式更加简洁而易记：先计算各数据平方的平均数，再减掉各数据平均数的平方，得出的就是方差.标准差公式的化简过程如下：

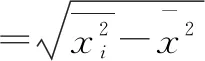
(2)

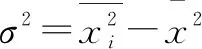
(3)