煤矿井底煤仓内散体颗粒三维结构分析
伍永平,刘明银,解盘石,郎 丁
(1.西安科技大学 能源学院,陕西 西安 710054;2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室,陕西 西安 710054;3.煤炭工业太原设计研究院集团有限公司,山西 太原 030001)
0 引 言
立井井底煤仓仓壁及围岩组成的支护系统处于深部高地应力环境下,并承受仓内散体贮料颗粒的反复加卸载作用,其力学响应较为复杂[1]。确定仓壁受力的关键是分析仓内散体颗粒运动过程中形成的力学结构承载结构及其对仓壁的力学作用机制。分析仓内散体贮料的力学结构形态,有助于进一步认清井底煤仓卸载超压现象的力学来源,为研究该类地下工程的稳定性提供理论支撑,对防治煤矿井底煤仓破坏也具有工程指导意义。
借助厚壁圆筒理论可得仓壁环向应力及径向应力分布特征,但仓内侧压力实际上为一动态变化数值。仓内散体颗粒处于不均匀流动状态,在其内部反复形成承载结构与结构失稳循环过程,在仓壁上出现卸载超压现象,该结构的性态及结构模型很难把握。黄松元在平面尺度上给出了压力拱的计算公式[2];许启铿等通过PFC3D对粮仓底部压力进行了数值模拟实验[3];WU等给出了井底煤仓力学模型,并分析了仓壁变形特征[4];闫浩等采用PFC3D对散体材料进行模拟实验,认为颗粒粒径、散体颗粒间摩擦因数对宏观应变量的影响较大[5];曹树刚等分析了散体矸石承载特性,大粒径的矸石间容易咬合形成稳定的承载结构[6];颗粒物质是大量离散的固体颗粒相互作用而组成的复杂体系,具有非连续和接触耗散等基本特征,强力链网络决定颗粒体系的宏观力学行为[7];楼晓明等探讨了散体材料对仓壁侧压力的计算方法[8];依据前人进行的地面筒仓、边坡等的颗粒模拟[9-12],岩石力学试验[13],PFC数值模拟实验[14-15],现有筒状筒体相关研究等[16-19],已经取得一定成果。
在卸料过程中该力学结构的不断形成及失稳造成了仓壁内侧压力发生动载超压现象。该承载结构作用在筒状仓壁内侧,引起仓壁内侧出现动态侧压力,侧压力的大小等于拱脚支承反力,方向相反。煤矿现场时常发生的“堵仓”事故,就是承载结构的外在表现。SRIVASTAVA等进行了散体颗粒的研究[20];FENG等模拟了地面小麦颗粒在筒内的结拱[21]。
由此可见,目前采用颗粒流方法对煤仓的研究多集中在颗粒流模型的构建、岩土体细观参数对破坏方式的影响、颗粒运动过程的模拟等方面,而对颗粒自身运动形成的结构及结构破坏过程中的力学机理分析等反应内部力学机理特征的分析和研究相对较少,多数研究没有从立体三维角度研究散体物料的内部力学承载结构分析。显然,井底煤仓的卸料过程为三维立体空间的运动过程,有必要进行三维空间散体颗粒流动过程中承载结构的研究。
假设该结构为“三维锥壳”形结构,分别从井底煤仓整体及仓内散体结构的角度出发,建立了三维力学模型及数值模型,考虑了其在地下工程中实际运行方式,运用散体力学,弹塑性动力学相关知识对力学模型进行了分析,揭示了散体颗粒引起的井底煤仓卸载超压作用机理。
1 散体“三维锥壳”结构力学模型
井底煤仓本质上仍然为一个立式混凝土筒状结构,在煤矿中,其处于不同岩层的围岩作用下,与岩体共同组成支护系统,来保障工作面生产出来的煤流暂时存储,并起到协调平衡前后主运输系统能力的作用,满足矿井安全生产要求。在不考虑围岩蠕变的情形下,此时围岩表现出与岩层性质相关的弹塑性约束,仓壁内侧压力与外侧压力大小相等,方向相反。仓壁动态侧压力主要受仓内散体颗粒运动性态及形成隐藏的承载结构决定,结合煤矿现场工程实践、物理相似模拟实验及数值模拟实验等研究可知,该结构分布形态类似“三维锥壳”形。
1.1 三维立体受力模型
仓内散体贮料(煤和矸石)在卸煤过程中散体贮料形成立体的类似“三维锥壳”结构。实际上,煤仓卸煤过程中是该结构不断的形成及失稳过程。结构支承点在仓壁的中下部区域,致使中下部区域侧压力系数增大,从而产生卸载超压现象。当该结构承载能力大于上部贮料静态及动态压力之和,即产生了散体物料结拱现象,也就是堵仓事故。目前煤矿井底煤仓采用的支护方式主要有混凝土砌碹支护和锚喷支护等,文中主要针对GB 50215—2015《煤炭工业矿井设计规范》中推荐的混凝土砌碹支护圆形直仓进行研究,分别从仓壁及散体颗粒2种情形进行研究。
1)取井底煤仓壁为研究对象时,仓壁主要承受外侧围岩约束,及上部覆岩对仓壁上口的荷载,同其它地下工程一样,井底煤仓壁是处于围岩约束之内的,起到支护围岩的作用,围岩又处于地应力作用范围内,这就造成了仓壁外侧承受围岩荷载。假设仓壁与围岩接触是紧密的,则仓壁整体结构受力如图1所示。
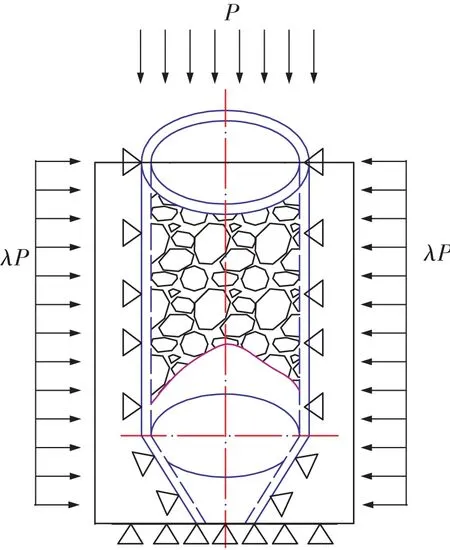
图1 仓内散体“三维锥壳”结构
2)取井底煤仓内散体贮料颗粒为研究对象时,对该模型的垂直剖面进行力学分析,仓内散体颗粒受力分析如图2所示。

图2 散体颗粒受力分析(满仓时)
1.2 散体颗粒运动方程
当井底煤仓下口给煤机开启时,仓内散体颗粒在自身重力作用下有向下运动的趋势,重力主要分成2部分,一部分为煤仓上部自然堆积体内的散体煤颗粒所受重力,除与散体颗粒的容重有关外,散体煤颗粒的自然安息角φ影响上部堆积体重量G1;另一部分为煤仓体内中下部贮存的煤颗粒所受重力G2,与下部漏斗与水平方向的夹角θ及仓筒半径R均有关。
分析图2,结合整体结构可得运动方程
(1)

由于井底煤仓内部的散体煤炭颗粒,在其自重的作用下要发生移动,而在锥形拱壳结构以上部分的散体遭受到了承载结构的抵抗进而在仓壁上造成了内侧压力。当卸煤时,散体贮料还会承受仓壁对附近颗粒的摩擦力作用,纵向上受重力及仓壁相互作用下产生向下的整体加速度。
从散体颗粒整体运动情况运动方程可知,仓内散体颗粒在卸料过程中由于受卸料口尺寸及仓壁约束限制并不像固体材料那样整体运动,为客观反映出散体颗粒内各部分的运动情况,采用离散元数值模拟是有效的手段,目前较为成熟的有PFC3D三维离散元数值模拟,可直观反映出井底煤仓内的三维运动过程,故文中进行了PFC3D数值模拟实验,对井底煤仓卸料过程作进一步研究。
2 PFC3D数值模拟实验
井底煤仓内散体颗粒主要为开采出来的煤炭颗粒及矸石颗粒,为典型的散体结构,PFC3D为理想的离散元数值模拟软件,通过数值实验可真实模拟其流动特性。
2.1 数值模型参数
在煤矿现场中,井底煤仓内的贮料主要为散体颗粒,来源于采掘工作面采出煤矸经运输系统装填而来。可简化为不同粒径分布下的散体颗粒而建立数值模型。由于PFC3D细观模型与实际颗粒不能一一对应,一般根据经验给出模拟颗粒粒径范围,散体煤的密度约为1 200 kg/m3,主要指煤堆的密度,而PFC3D中的密度指的是颗粒密度。实验参数见表1。

表1 离散元模拟实验参数
2.2 离散元数值模型
利用PFC3D内嵌的Fish语言编写模型数据,用球单元近似模拟散体煤炭颗粒,用墙单元模拟井底煤仓壁。实验模拟颗粒堆总高度为20 m,整个颗粒堆分6层铺设不同的颜色区分,每层颗粒堆厚度相同,模拟采用Ball Porosity为0.5,选取颗粒半径为0.4~0.8 m,颗粒服从均匀分布,则最终模型生成的颗粒数为1 101个,1号数值模型如图3(a)所示。
为了研究颗粒流动形态,并考虑散体颗粒粒径对结拱的影响,另外进行了一组实验,粒径分布区间为0.2~0.6 m,当Ball Porosity值为0.3时,煤仓结拱现象消失,此时共计生成的颗粒数为4 040个,2号数值模型如图3(b)所示。
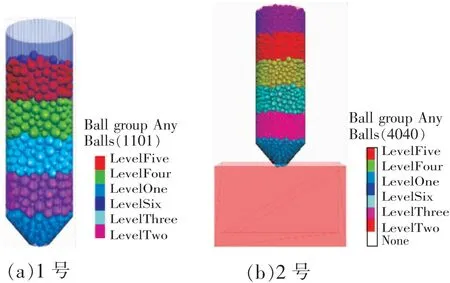
图3 井底煤仓离散元数值模型
2.3 数值实验结果分析
根据实验测得的数据,选取靠近筒壁附近的小范围测量圈的数据近似作为井壁仓壁处的受力状态,得出不同深度处得仓壁结拱如图4所示。

图4 散体颗粒结拱
散体颗粒并不像液体那样“流动”,而是在重力作用下滚动、滑动及沉降。散体颗粒的大小、形状、质量、粘滞性等几何、物理特性,均可能影响其本身的运动,从而影响总体的“流动”。
考虑装煤过程为自由落体,实验可描述颗粒在三维空间里的运动轨迹,碰撞恢复过程,散体煤或矸石从仓内流出的过程,形成卸载超压现象。
2.4 粒径对结拱现象的影响
进一步分析2号数值模拟实验,其流动形态如图5所示。当第1层散体颗粒流出未完成时,上部第2组的部分颗粒已经由煤仓中部流出,如图5(a)所示,此时时步为9 877步;9 877到27 371步区间为下部一、二的2层的混合流出形态,如图5(b)所示;后续就只有第2层颗粒流出,如图5(c)所示。其余各层组流动形态类似,不再赘述。

图5 不结拱时的散体流态
通过PFC3D数值模拟实验,十分直观的反映出了井底煤仓卸料过程的内部散体结构模型的形成及模拟破坏过程。实验中发现由于部分下部贮料颗粒还未完全流出,其上一层散体颗粒则先于下层颗粒而流出仓体,这说明仓内散体贮料结构在上部颗粒载荷的动力作用下,在“三维锥壳”的壳顶首先失稳,进而在重力作用下穿过第1层未放出部分颗粒而先流出了井底煤仓。这也说明了在煤仓散体流动形态上,位于煤仓轴心中部的散体颗粒比煤壁处的颗粒流动速度更快。
3 仓壁水平动侧压力表达式
3.1 “三维锥壳”相关理论
郑长卿研究了锥壳结构的稳定性;PRADERAMA 等探讨了圆锥壳在压缩作用下的塑性倒塌响应;孙博华等分析了扁锥壳的大挠度问题[22-24]。“三维锥壳”为一种空间薄壳体,该空间壳体形态结构介于柱壳与圆壳之间;三维锥壳按其本身结构划分由3部分构成:壳顶、壳肩、壳基;按其空间形态可划分为规则的圆锥形形态和不规则的曲面形态;规则形态主要为直线绕纵向轴线旋转而来的三维对称旋转壳体,不规则锥壳包括其它具有一定厚度的曲面形成的内部孔洞,表现出具有壳状承载结构的三维空间壳体。
3.2 井底煤仓三维物理模拟实验结果
为研究井底煤仓卸煤过程中形成的散体承载结构,通过三维物理相似模拟实验发现了类似于现场及数值模拟的“三维锥壳”结构,如图6所示。
从图6可以看出,在井底煤仓三维物理模拟试验中当模拟卸煤过程时,“三维锥壳”下部煤炭颗粒已经放出,而上部仓体内的煤炭颗粒仍未移动,锥壳起到了很好的承载作用,物理模拟实验结果与现场及数值模拟具有较好的一致性。
3.3 “三维锥壳”结构力学分析
仓内散体颗粒三维承载结构作用在仓壁上产生侧压力Tx,仓壁侧压力与仓壁对锥壳的反作用力之间相互平衡。为便于分析,从散体力学角度进行研究仓壁侧压力的计算。水平侧压力是由于仓壁对散体颗粒的束缚而产生的反作用力,仓壁对散体的作用力企图改变其向外垮落的趋势。
在井底煤仓内距散体三维结构底面取出一个厚为dR的成拱壳单元,在从下及上的垂直压力(静载q和Δq)、自重及摩擦力的作用之下,这个单元是在平衡状态,如图7所示。

图7 “三维锥壳”受力分析
令散体的弹性模量为E,横向变形系数μ为常数,则水平与垂直压力之间的关系式将为
(2)
Tx=Vx
(3)
Tz=q+Δq+G0-Vz
(4)
该单元在垂直方向的相对压缩量为
(5)
因此拱形贮料的单位重量与作用在贮料上的压力间的关系式将为
(6)
式中q为上部贮料的静压力,N;Δq为上部贮料流动时产生的动态压力,N。
由于分母中第2项要比1小的多,可用下列方程式来代替,如曲线3所示。
(q+Δq)(1+TzB)
(7)

(8)
竖直方向为z,则dz=dR·sinθ
所取出的单元的平衡条件为
(Tz+dTz)A-TzA-γAdz+TxμLdz=0
(9)
式中A为井底煤仓水平截面面积,m2;L炎水平截面的周长,m;μ为散体贮实对井底煤仓壁的摩擦系数。
将式(2)及式(8)中的γ和B代入式(9),消去A并合并同类项可得
dTz-(q+Δq)(1+TzB)dz+λTzμdz=0
用dz除各项并根据z=0,Tz=0这一边界条件进行积分,可得以下结果
(10)
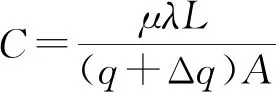
从式(10)可知,当满仓时,井底煤仓壁侧压力增长的规律,如图8所示。

图8 侧压力分布规律
从式(10)可见,决定侧压力Tz的值变化规律,取决于分母中的项
的大小,即(C-B);另一个影响参数为分子中的项
的大小,即分子中与(C-B)相关的幂函数部分,故有必要对影响侧压力值得(C-B)的大小作进一步讨论。该规律简单分析如下
1)当B>C时,在z→∞时,如曲线1所示,压力很快变成无限大。
2)当B=C时,计算该不等式得
Tz=λ(q+Δq)z
即压力增长与深度成正比,如曲线2所示。
3)当B 4)当B=0时,(只有在E=∞时才有可能),公式(10)变成Janssen公式而得出上述3种情形为最小的压力值,如曲线4所示。 由于散体颗粒堆积高度的变化,对某一具体深度处井底煤仓壁侧压力也是不断变化的。井底煤仓散体“三维锥壳”结构在动力荷载下,由于惯性产生于静力荷载不同的运动形式。很显然,与静力学中很小的静载荷仅产生很小的静位移截然不同,如果小的扰动载荷变成为动力荷载,产生的动位移则可能很大。 工作面来煤经过顺槽及大巷皮带运输到煤仓上口位置,后落入煤仓造成力学冲击荷载作用。该过程可由动量定理分析有 (F-mg)t1=mv (11) (12) 式中v为颗粒运动至煤仓储煤面的速度,m/s;m为颗粒的质量,kg;F为颗粒对煤仓的冲击作用力,N;z为贮料面的纵向坐标,m;g为加速度,m/s2。 (13) 卸煤时间与煤仓容量及下部漏斗口卸出煤的流量有关 V=Q1·t2 (14) 式中V为煤仓容量,m3;Q1为煤炭流量,m3/s;t2为满仓至空仓的卸煤时间,s。 卸煤过程中,仓内散体的下部分层颗粒流动速度大于上部分层,从而使下口附近物料先流出。当某一分层由于散体颗粒间的内聚力作用,挤压造成机械咬合等作用时,就易于形成内部承压锥壳结构,且具有一定的承载能力。 (15) 由于在煤炭生产过程中,煤炭颗粒大小分布是不均匀的,往往混入煤末或煤泥,此时贮料会具有一定得粘性,这样在考虑不同颗粒材料性质的时候,分析卸料速度时可按标准物料和粘性物料区分。 4.3.1 标准物料 当散体颗粒较均匀干燥时,认为服从标准物料特性,对于理想物料的“标准”排料形式,卸料孔作为中心布置时,其排料速度v可按下式计算 (16) 式中Θ为流动系数,决定于物料的流动性及其粒度,1。对于干燥易流的散粒物料,可取Θ=0.6;对于块状物料,取Θ=0.4;对于尘状物料及湿粉状物料,取Θ=0.2;R′为水力半径,m。 对于“标准”排料形式,物料由排料孔卸出的速度,随排料尺寸的增大而提高。 4.3.2 粘性物料 极限半径 (17) (18) (19) 式中τ0为物料的初始切应力,Pa;ρg为物料的堆积质量,kg;f为物料的内摩擦系数。 可见,卸料速度不仅与物料的粒径有关系,还与物料内摩擦系数、内摩擦角等均有关系。 散体颗粒所形成的承载结构反应在仓壁上,即为仓壁侧压力,井底煤仓壁的侧压力是与时间相关的函数,用q(t)表示,若某一深度,仓壁侧压力随时间的变化如图9所示,即 图9 仓壁荷载 若q(t)>0,dq/dt≥0,则仓壁处于加载状态,q(t)>0,dq/dt≤0,则处于卸载状态。 仓内某一给定深度处的散体应力σ与加卸载路径密切相关,随着上部颗粒的流入而压力增加,下部承载结构散体颗粒的压实,表现出明显的塑性特性,从图9知,若q0≤σ0,σ0为简单拉伸时的屈服应力,则整个加载和卸载都处于弹性状态,若q0>σ0,则加载阶段服从塑性本构关系。 井底煤仓内散体颗粒应力应变加卸载路线如图10所示。 从图10可知,散体介质颗粒内部的应力应变曲线加载与卸载过程是不重合的,实验中表现为卸载压实现象。 图10 应力应变加卸载路线 1)煤矿井底煤仓内部散体贮料卸料过程中存在着三维锥壳结构,该结构的不断形成和失稳对仓壁产生动态压力,形成井底煤仓出现卸载超压现象。 2)井底煤仓壁三维结构稳定性受仓内散体贮料颗粒尺寸影响较为明显,当实验粒径分布达到0.2~0.6时,结拱效应消失,散体力学结构稳定性受内摩擦角及内聚力影响次之,位于煤仓轴心中部的散体颗粒比位于仓壁附近的颗粒流动更快。 3)通过理论分析结合数值模拟、三维物理模拟实验,分析了“三维锥壳”结构力学模型,且其承载能力具有时间特性,揭示了井底煤仓卸料过程中卸载超压现象发生的主要力学诱因。4 散体卸料运动的时间特性
4.1 装煤过程动量分析及冲击时间

4.2 卸煤时间分析
4.3 不同物料卸料速度计算


4.4 循环荷载下侧压力与时间的关系


5 结论

