基于贝叶斯理论面波频散曲线随机反演
刘辉,李静,2,曾昭发,王天琪
(1.吉林大学 地球探测科学与技术学院,吉林 长春 130021;2.地球信息探测仪器教育部重点实验室 (吉林大学),吉林 长春 130026)
0 引言
瑞利面波是一种由纵波与横波干涉形成沿自由表面传播的地震波。1887年,英国学者Rayleigh首先发现并证明均匀半空间中瑞利面波的存在[1-2]。面波频散曲线反演是获取浅地表地下空间、深部岩石圈和地球构造横波速度的重要方法技术[3-5]。Park等[6]提出的多道面波分析方法(MASW)广泛应用于浅地表面波数据采集处理;Xia等[7]采取奇异值分解和L-M方法,实现了瑞利波基阶频散曲线反演;Song等[8]使用Occam算法进行一维频散曲线反演后获得了一个含低速层的拟二维横波速度剖面;鲁来玉等[9]和罗银河等[10]分别采用遗传算法和最小二乘方法实现了不同尺度多阶面波频散联合反演,可有效提高单纯只依靠基阶面波的反演精度。
常规基于迭代的最小二乘线性反演方法依赖于初始模型且存在多极值、容易陷入局部最小、反演精度低等问题。基于全局最优的非线性反演方法由于不依赖于初始模型,已广泛应用于地球物理反演。Beaty等[11]利用模拟退火法在一定概率下可以接受劣解的搜索方式实现了多阶瑞利波联合反演;宋先海等将模式识别算法[12]和粒子群算法[13]应用到瑞利波频散曲线反演中;蔡伟等[14]将萤火虫和蝙蝠群智能算法应用于瑞利波频散曲线反演;于东凯等分别利用改进蜂群算法[15]和蚱蜢算法[16]实现了瑞利波频散曲线反演。在天然地震被动源面波成像研究中,Aki[17]提出利用背景噪声研究地下结构,从台阵信号中提取瑞利波频散信息的空间自相关法(SPAC);徐佩芬等[18]利用SPAC法从微动信号中提取频散曲线并利用遗传算法进行反演获得S波速度结构;张宝龙等[19]利用扩展空间自相关法(ESPAC)提取频散曲线结合面波层析成像技术获得了地壳浅层三维S波速度结构。虽然传统算法如遗传算法具有对初始模型要求宽松、无需求梯度、易于实现并行化等优点,较适合于解决非线性、多参数的瑞利波频散曲线反演问题,但也存在计算量大、局部搜索能力差和收敛稳定性差等缺陷,使其在频散曲线反演中受到一定的限制。
针对上述算法中存在的问题,结合前人研究成果,本文提出一种基于贝叶斯马尔科夫蒙特卡洛(MCMC)理论的随机反演方法,通过先验信息建立解空间,采用马尔科夫链扰动模拟算法,计算模型频散曲线与实际曲线的似然函数,再利用转移概率规则引导搜索过程,可得到与实际频散曲线匹配最佳的最优解,获得大概率的横波速度后验概率分布,从而减少反演的多解性,提高分辨率。本文通过典型理论模型和实测面波数据验证基于贝叶斯理论的随机反演方法的可行性。实测数据应用中,利用GPR解释剖面进行深度约束作为先验模型信息,在此基础上开展面波随机反演,从而获得近地表横波速度结构。
1 贝叶斯随机反演原理
根据贝叶斯理论可以用d表示实际数据,用m表示横波(Vs)速度模型:
p(m│d)=p(d│m)p(m)/p(d),
∝p(d│m)p(m),
(1)
其中,p(m│d)是模型在给定数据的情况下的后验概率,p(m)是引入数据之前有关模型的先验信息,p(d│m)是似然函数(在给定特定模型(m)的情况下观察到实测数据的概率),p(d)是实际数据的准确性,与m无关可以视为常数。
实际数据由N对频率(f)和瑞利波相速度(PV)组成的频散曲线以及偏差(σ)组成:
d=[f1f2…fN,PV1PV2…PVN] , (2)
σ=[σ1σ1…σN] 。
(3)
相速度偏差(σ)是表示所拾取的频散曲线的不确定性的量,其大小可取频散能量图的各频率的相速度能量集中的区间长度。
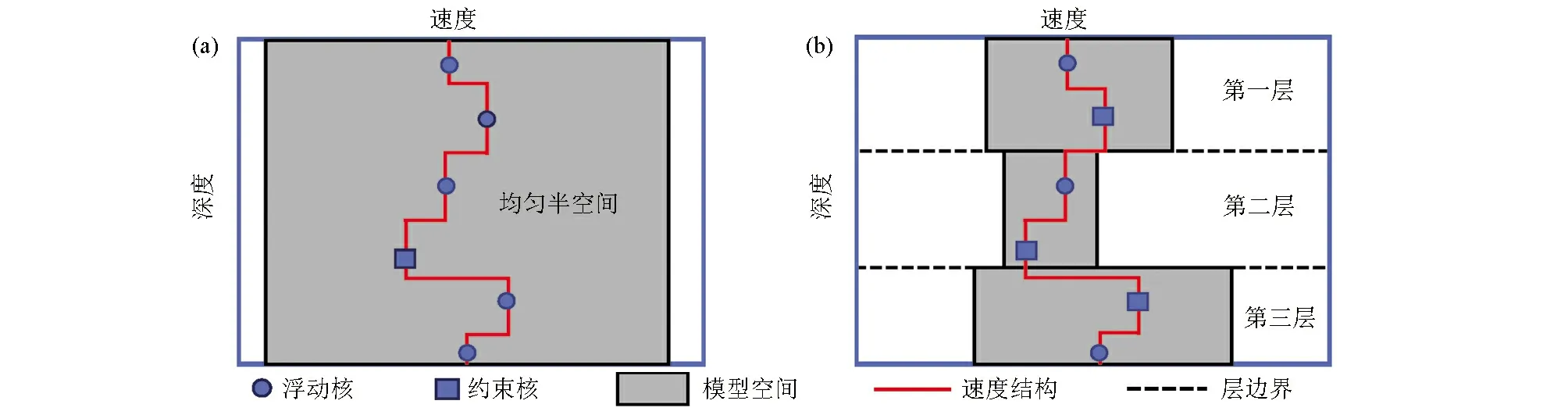
使用Voronoi核来表示模型参数[20]。如图1所示。灰色为vs模型空间,每一层都包含一个约束核和多个浮动核,在每个深度的vs值由离其最近的核决定,Voronoi核在模型空间中移动,其中浮动核可以在模型空间的深度范围内移动,而约束核只能在其固定的层移动,于是模型参数为:
m=[k,dp1,dp2,…,dpk,vs1,vs2,…,vsk,I,
dpc1,dpc2,…,dpcI,vsc2,…,vscI],
(4)
式中,k是浮动核的数量,I为约束核的数量,dpk为浮动核的深度,vsk是浮动核的横波速度,dpci是约束核的深度,vsci是约束核的横波速度。
先验信息p(m)可以分为两部分:
p(m)=p(m|n)p(n) 。
(5)
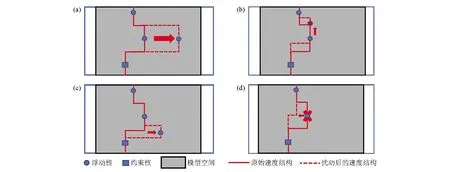
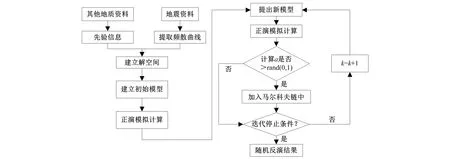
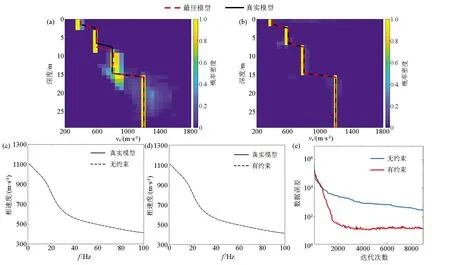
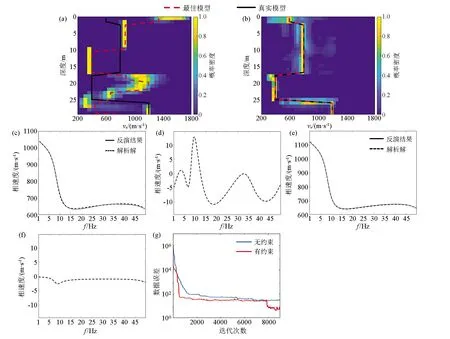
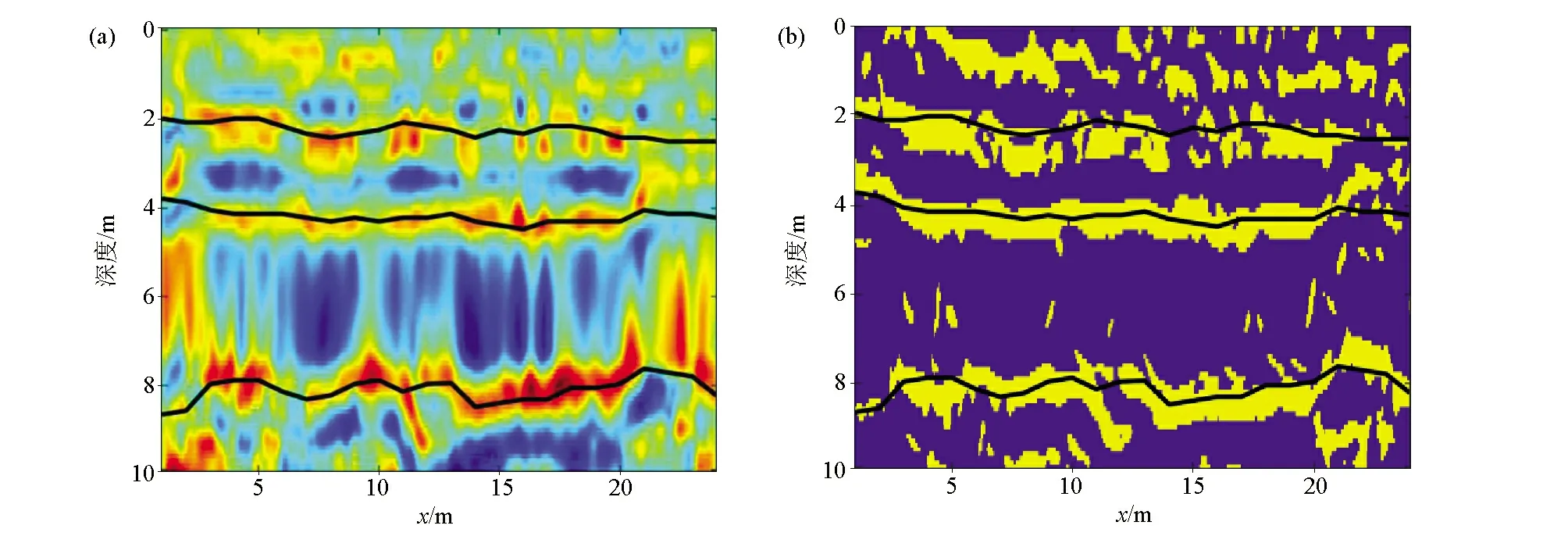
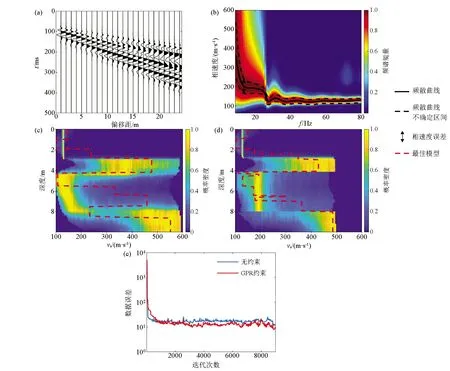
其中,p(n)是Voronoi核数的先验,设区间I={n∈N|nmin (6) 其中Δn=(nmax-nmin),由于Voronoi核的深度c和速度v相互独立,所以p(m|n)可拆分为: p(m|n)=p(c|n)p(v|n) 。 (7) 速度的先验区间为J={vi∈R|vmin (8) a—无先验信息的vs均匀半空间模型;b—有先验信息的三层vs空间模型a—1 layer model without constraints;b—3 layer model with GPR constraints图1 使用Voronoi核进行模型参数化Fig.1 Model parameterization using Voronoi nuclei 其中,Δv=(vmax-vmin)。由于每个Voronoi核的速度相互独立,则: (9) (10) 结合式(5)~(10)先验概率密度函数: (11) 似然函数p(d│m)表示在给定模型m的情况下观测到实际数据的可能性,实际上是通过对模型m进行正演模拟得到频散曲线G(m)并计算其与实际频散曲线的相似度来实现的。假设数据di(i=1,2,…,Ndata)的每对频率fi与相速度PVi相互独立,则似然函数: 对每个新模型进行正演计算以确定其是否达到可接受的标准: 式中:q(m′|m)是从模型m变化到模型m′的概率,q(m|m′)是从模型m′变化到模型m的概率,J为雅可比矩阵。对于不改变模型尺度,改变核的vs(图2a)和改变核的深度(图2b),其扰动是对称的,即从m变化到m′的概率等于从m′变化到m的概率: a—改变核的vs;b—改变核的深度;c—产出一个浮动核;d—移除一个浮动核a—change vs of a nuclcus;b—move a nuclcus to a different depth;c—give birth to a new floating nucleus;d—remove a floating nucleus图2 模型的4个扰动方式Fig.2 Illustration of four possible perturbations to a current model (14) (15) 所以这两种扰动: q(m′|m)=q(m|m′) 。 (16) 对于产生一个新的浮动核(图2c)和移除一个浮动核(图2d),模型尺寸发生了变化,且扰动不对称。由于Voronoi核的深度和速度相互独立,对于产生新核: (17) (18) 对于移除浮动核: (19) 式(13)中,J是从模型m变化到模型m′的雅可比矩阵,表示m与m′的尺度变化,即只有在两个不同尺度的模型之间扰动(产生或移除Voronoi核)时才需计算雅克比矩阵,如果当前模型与扰动模型具有相同尺度,则|J|=1,可以忽略。对于产生Voronoi核,从m到m′的双射映射h: (20) (21) vi是新核位置扰动前的速度值。模型空间分为离散空间(核深度)和连续空间(速度),uc是用于离散空间转换的离散变量,而uv是用于连续空间转换的连续变量。Denison等[22]研究表明对于离散变换,雅克比项|J|=1,可以忽略,所以雅克比项仅考虑以下变量: (22) 因此: (23) 对于移除Voronoi核,|J|death=|J-1|birth=1,所以对于上述4种扰动,雅克比项都等于1,可以忽略。 在求得新模型的a值后,将其与随机数u~U[0,1]进行比较:如果a>u,则接受新模型m′并将其添加到链中,如果a 面波随机反演的基本流程如图3所示,其基本实现流程如下: 图3 面波随机反演基本流程Fig.3 Basic flowchart of surface wave stochastic inversion 1)根据地震面波资料提取频散曲线; 2)根据先验信息建立解空间; 3)对解空间内的随机模型进行预反演,其结果作为反演的初始模型m; 4)计算初始模型m的理论频散曲线与似然函数; 5)随机扰动产生新模型m′,并计算理论频散曲线及似然函数; 6)计算a,若a>u(0,1),则将新模型m′加入到马尔科夫链中,否则保留原模型m; 7)重复步骤5)、6),直至满足迭代停止条件。 为验证本文所述随机反演方法,分别采用4层vs递增模型和4层含低速夹层模型开展反演测试。表1给出了4层vs递增模型的基本参数。图4为4层vs递增模型基阶频散曲线的反演结果。图4a为无约束反演结果,反演结果(最佳模型)与真实模型在深度7 m的第2、3层分界面处有所差异,vs的后验概率分布与真实模型基本拟合;图4b为带约束反演结果,vs的先验约束根据频散曲线设为300~1 300m/s(vs的下边界为0.9倍的相速度最小值;vs的上边界为1.1倍的相速度最大值)。深度约束为3层,分别为0~2 m、3~15 m、16~30 m,相比于无约束反演结果,带约束反演最佳模型和vs的后验概率密度分布与真实模型更好地吻合。图4c为无约束反演的反演结果(最佳模型)与实际模型频散曲线,两条曲线在所有频率范围内基本重合。图4d为有约束反演的最佳模型与实际模型频散曲线。图4e为两种模式下的迭代误差曲线,有约束反演(红线)迭代1 000次左右就能将误差降低到无约束反演(蓝线)迭代8 000次的误差大小,且目标函数最终的迭代误差也更小。该模型测试验证了对于速度递增模型,本文提出的随机反演策略即使在无约束条件下也能得到较好的反演结果。 表1 4层vs递增模型参数 a—无约束反演结果;b—有先验约束反演结果;c—无约束反演的最佳模型与实际模型频散曲线;d—有先验约束反演的最佳模型与实际模型频散曲线;e—迭代误差曲线a—inversion results without constraints;b—inversion results with prior constraints;c—dispersion curves of the best fitting model and true model for unconstrained inversion;d—dispersion curves of the best fitting model and the true model with prior constraint inversion;e—misfit iteration curve图4 4层vs递增模型基阶频散曲线反演Fig.4 Fundamental dispersion curve inversion of four-layer vs increasing model 表2给出了4层含低速夹层测试模型的基本参数。图5为4层含低速夹层模型基阶频散曲线的反演结果。图5a为无约束反演结果,最佳模型(反演结果)与真实模型误差较大;图5b为有约束反演结果,此处vs的先验约束范围同样设为300~1 300 m/s,深度约束为3层,分别为0~2 m、3~17 m、18~30 m,最佳模型和vs的后验概率密度分布与真实模型基本吻合。图5c为无约束反演的最佳模型与实际模型频散曲线,两曲线基本重合,最佳模型与真实模型的反演误差主要来自于基阶波对低速层的不敏感以及无约束随机反演局部搜索能力差。图5d为无约束反演频散曲线误差,可以看出在不同频率范围内存在一定的频散曲线拟合误差。图5e和图5f为带约束反演的最佳模型与实际模型频散曲线和频散曲线误差,相比无约束反演,有约束反演误差较小且整体几乎等于零,表明了约束随机反演具有较高的反演精度。图5g为两种模式下的迭代误差曲线,无约束反演(蓝线)在迭代8 000次左右时误差达到最小且趋于稳定,而有约束反演(红线)迭代3 000次左右就能达到同样的误差大小且最终的迭代误差也更小。上述模型测试表明,对于含低速夹层的速度结构,由于面波频散信息复杂,存在模态混叠现象,需要在一定约束条件下才能得到满意的反演结果。 表2 4层含低速夹层模型参数 a—无约束反演结果;b—有先验约束反演结果;c—无约束反演的最佳模型与实际模型频散曲线;d—无约束反演频散曲线误差;e—有先验约束反演的最佳模型与实际模型频散曲线;f—带约束反演频散曲线误差;g—迭代误差曲线a—stochastic inversion results without constraints;b—stochastic inversion results with prior constraints;c—dispersion curve of the best fitting model and true model for unconstrained inversion;d—error of dispersion curve for unconstrained inversion;e—dispersion curves of the best fitting model and the true model with prior constraint inversion;f—error of dispersion curve with prior constraint inversion;g—misfit iteration curve图5 4层含低速夹层模型基阶频散曲线反演Fig.5 Fundamental dispersion curve inversion of low-velocity layer model 为进一步验证随机反演方法的可行性与可靠性,采用浅层主动源面波实测数据开展横波速度反演测试。实测数据来自于中国安徽省淮南市某校园操场[23],开展的地球物理方法包括浅层主动源面波与探地雷达(GPR)方法。面波数据沿测线共24炮,采用24个4 Hz检波器,道间距为1 m,最小偏移距10 m,震源采用锤击震源;GPR数据包含以第13炮集记录测量点为中心的共中心点道集(CMP)记录以及覆盖整个地震测线的共偏移记录。图6a为处理探地雷达数据得到的GPR剖面。图6b为基于卷积神经网络(CNN)[24]进行GPR层界面自动识别结果,根据GPR剖面与CNN识别结果将地下划分为4层,黑色实线为层界面。图7a为经过处理仅保留面波成分的第13炮地震记录。图7b为由炮集记录提取的频散能量,根据能量的最大值提取出基阶频散曲线。图7c无约束反演结果,根据vs的后验概率分布可以看出,在10 m深度范围内地下共4层,其中第3层为低速夹层,深度为4 ~8 m,反演的最佳模型在浅层与vs后验概率分布基本匹配,但深层误差较大。图7d为GPR结果深度约束反演结果,vs约束根据频散曲线设为100~500 m/s,与无约束反演相比,第3层的vs后验概率分布更加集中,且与反演的最佳模型更加匹配。图 7e为迭代误差曲线,可见在有约束条件下,随着迭代次数的增加,GPR约束反演的收敛速度更快。 图6 探地雷达处理剖面(a)与基于卷积神经网络的GPR层界面识别结果(b)Fig.6 Processed GPR profile(a)and GPR layer recognition results based on Convolutional Neural Networks(b) 将上述一维反演结果按照空间位置分布组合成拟二维剖面,如图8所示。图8a为无约束反演结果组合成的拟二维剖面,黑色实线为GPR分层界面,从图中可以看出:面波频散反演的横波速度结果前两层分界面与GPR数据基本匹配,但后3层分界面误差较大。图8b为GPR深度约束反演结果组合成的拟二维剖面,前3层分界面与GPR数据基本匹配,虽然底层界面仍然存在误差,但相比无约束反演,误差已经有所降低。 结合前人钻孔研究成果[25],地下结构分层解释结论为:第1层由松软的沙子、砾石、土壤组成,深度为1~2.2 m,横波速度为100~150 m/s;第2层由紧凑且致密的沙子、砾石、土壤组成,深度为2.2~4.2 m,横波速度为350~500 m/s;第3层为黏土,深度为4.2~8 m,横波速度为120~180 m/s;基岩层由风化程度不同的砂岩组成,深度大于8 m,横波速度为400~500 m/s。前人钻孔深度解释与本文约束随机反演横波速度结构有较好的吻合性。 a—第13炮地震记录;b—由炮集记录提取的频散能量;c—无约束反演结果;d—GPR深度约束反演结果;e—迭代误差曲线a—one shot gather of 13th shot;b—extracted dispersion curve;c—unconstrained stochastic inversion result;d—stochastic inversion with GPR constrained;e—iterations图7 实测数据反演Fig.7 Inversion results of real surface wave data a—无约束反演结果组合成的拟2D剖面;b—GPR深度约束反演结果组合成的拟2D剖面a—2D velocity profile of unconstrained stochastic inversion;b—2D velocity profile of GPR constrained stochastic inversion图8 拟二维剖面反演结果对比Fig.8 Comparison of quasi-two-dimensional profile inversion results 本文提出了基于贝叶斯反演理论的随机反演方法并应用于面波频散曲线反演。利用先验信息深度约束分别对理论和实际面波数据进行无约束、有约束随机频散反演对比测试,结果表明: 1)随机反演方法是一种高效、稳健的反演方法,具有较高的全局寻优能力,且不依赖于初始模型。 2)带约束的随机反演可以有效且可靠地应用于面波频散曲线反演中,与传统无约束反演相比,随机反演可以很好地融合先验信息,减少多解性,提高反演效率与反演精度。 本文所使用的先验约束为GPR深度约束,而vs速度范围约束是由频散曲线确定的,如果实际测区有地质资料可以确定地下各层的vs速度范围,将其加入到先验约束中可以进一步减少多解性。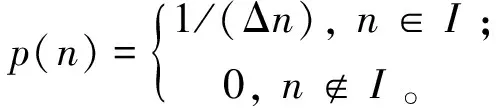
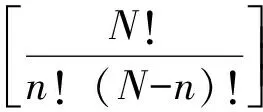
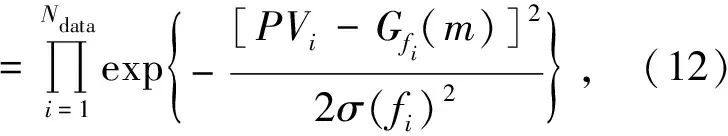

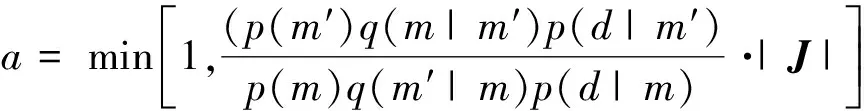
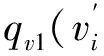

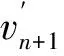
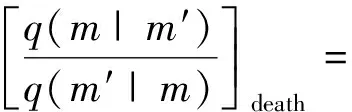

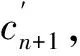
2 面波频散随机反演模型测试


3 实测地震数据测试

4 结论

