复杂异常体模型下的三维MT倾子正演模拟

田郁，乐彪

(1.贵州省地质调查院，贵州 贵阳 550000； 2.贵州省地质物探开发应用工程技术研究中心，贵州 贵阳 550000； 3.贵州正业工程技术投资有限公司，贵州 贵阳 550000)

0 引言

大地电磁测深法(MT)应用领域较广[1-2]，野外观测参数较多，可转换出20多个不同参数供地质解释使用，目前仅视电阻率和阻抗相位用于定量解释，严重的浪费了MT的实测资料[3-4]。倾子作为大地电磁测深法的实测参数之一，主要表征垂直磁场Hz与水平磁场(Hx，Hy)之间的变化关系，反映了地电构造的横向不均匀性。目前对倾子资料的研究局限于简单的理论模型研究，随着电磁技术的发展，使得对倾子资料的深入研究成为可能。

早期，国内外不少学者分析研究了倾子资料特征，发现倾子对横向不均匀性反映灵敏，且受静态效应影响较小[5-8]，同时对倾子资料的二维正演模拟进行了大量研究工作，得出倾子资料能有效地识别异常体的横向边界，且对多个异常体边界的识别能力优于视电阻率参数[9-12]，之后倾子资料逐渐被应用于资料解释中，用来寻找断裂、构造破碎带等，判断其位置、走向和规模[13-15]。然而，简单的二维异常体模型研究难以全面总结倾子资料特征，随着计算机科学和计算机软硬件的发展，MT正演模拟研究逐渐由二维转向三维，但倾子资料的三维正演模拟研究相对较少，且建模较单一，分析不够全面[16-18]。有限单元法的逐步成熟提高了复杂介质正演模拟的精度，本文基于三维大地电磁有限元正演模拟[19-22]，进一步分析研究复杂组合异常体模型下的三维倾子响应特征及变化规律，从不同切片图中总结倾子资料特征，为倾子资料在实际地球物理解释中的应用提供理论依据。

1 三维倾子定义及计算公式

根据电磁场理论，从麦克斯韦方程组出发，把大地电磁测深看成似稳态的电磁场问题，忽略位移电流对电磁场的影响，则可以推导出三维模型下电场E和磁场H各分量之间存在如下关系式：

(1)

方程组(1)说明了电场各分量与磁场各分量之间的变化关系，既包含垂直磁场分量与电场横向变化的关系，也包含了垂直电场分量与磁场横向变化的关系，同时说明了电磁场的变化与介质特性之间的相互影响关系。

假设场源是高空垂直入射的均匀平面电磁波，在地表的电磁场垂直分量Ez和Hz为0。当平面波进入一维介质后，感应场无磁场垂直分量。只有当地下电性结构为二维、三维时，才会产生磁场的垂直分量Hz。在实际地电构造中，根据边界条件，空气的电阻率约为108Ω·m，则地表处的Ez≈0，则方程组(1)的左边三式可以化简为：

(2)

根据大地电磁传输函数，电磁场各分量之间的关系如下：

Ex=ZxxHx+ZxyHy

Ey=ZyxHx+ZyyHy

Hz=TzxHx+TzyHy

(3)

式中：Zxx、Zxy、Zyx、Zyy为阻抗张量，Tzx、Tzy为倾子矢量，两者均包含地下介质电性的非均匀性信息。

将式(3)中的前两式代入式(2)中的第三式的左边，第三式代入式(2)的右边，则有：

iωμ[TzxHx+TzyHy]。

(4)

上式左边包含大地电磁阻抗张量元素与水平磁场分量(水平梯度)，右边则是倾子矢量的表达式。

前面已论述了基于在平面波入射的条件下，水平磁场是均匀的，因而其水平梯度可以忽略，由上式可以得出如下表达式：

(5)

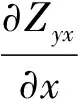
2 三维大地电磁倾子正演响应

构建不同的三维异常体模型，如单个低阻异常体模型、复杂组合异常体模型(左右组合、上下组合)等，采用有限单元法四面体剖分法进行三维倾子正演模拟，四面体能更好地模拟复杂地质体，分别计算了多个频率下的三维倾子正演响应，频率的改变仅影响倾子响应幅值的大小，不影响倾子响应特征规律，本文选取0.1 Hz下倾子资料在不同平面的响应切片图，分析对比倾子实部、虚部以及振幅对异常体的反映情况，总结三维电性结构情况下倾子资料的响应特征和规律。

2.1 单个低阻异常体模型

三维低阻异常体模型在不同平面的示意图如图1所示，其中异常体电阻率为10 Ω·m，围岩电阻率为100 Ω·m，异常体在XY平面关于坐标中心对称，沿X方向的宽度为1 km，Y方向的长度为2 km，Z方向的高度为2 km，顶面埋深为500 m。

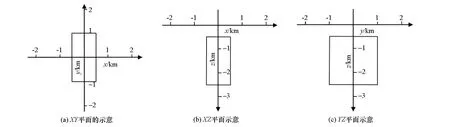
图1 三维低阻异常体模型在不同平面的示意Fig.1 Different planes of three-dimension low resistivity abnormal body model

图2、图3、图4分别为计算频率为0.1 Hz时低阻异常体模型的三维倾子响应在XY、XZ、YZ平面的切片图，分别给出了Tzx和Tzy的实部、虚部和振幅平面图。图中黑色矩形为异常体在各个平面的投影，从图中可以看出异常体模型在各个平面均对称，倾子资料的各个分量也均呈对称状态，虚部和实部的异常形态基本一致，倾子虚部异常值较实部异常值偏小。在XY平面切片图中，异常体的中心均位于倾子各个分量为零的等值线上，其中Tzx的实部、虚部以及振幅值在异常体的上下边界处表现为最大值和最小值，Tzy的实部、虚部以及振幅值在异常体的左右边界处表现为最大值和最小值。异常体边界即为电性分界面，倾子表现为最值，结合Tzx和Tzy倾子响应图可以很好地识别出异常体在XY平面的中心位置及4个边界的位置。在XZ和YZ平面切片图中，由于倾子虚部形态与实部一致，分别只给出了效果相对较好的倾子响应图。同样可以看出异常体在XZ和YZ平面的中心位于倾子实部和振幅的两个异常值区域接触带的中心，且在异常体的边界处倾子响应值均为最大值或最小值，异常体的大小与倾子异常区域对应。结合倾子响应资料在不同平面的切片图，可判断出异常体在各个平面的中心位置及边界，从而判断出异常体的大小及埋深。

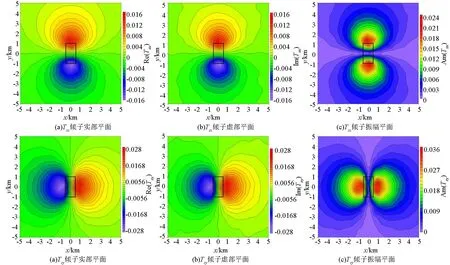
图2 低阻异常体模型倾子响应在F=0.1 Hz的XY平面的切片Fig.2 Section diagram of low resistivity abnormal body model with tipper response in the XY plane at F=0.1 Hz

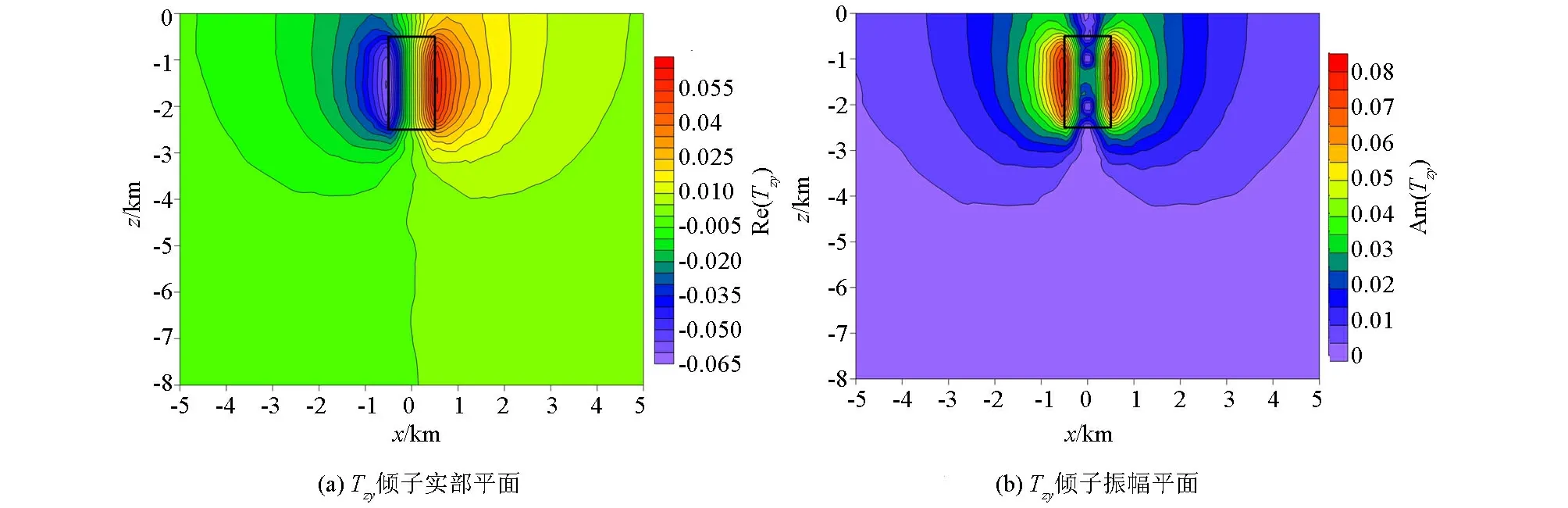
图3 低阻异常体模型倾子响应在F=0.1 Hz的XZ平面的切片Fig.3 Section diagram of low resistivity abnormal body model with tipper response in the XZ plane at F=0.1 Hz

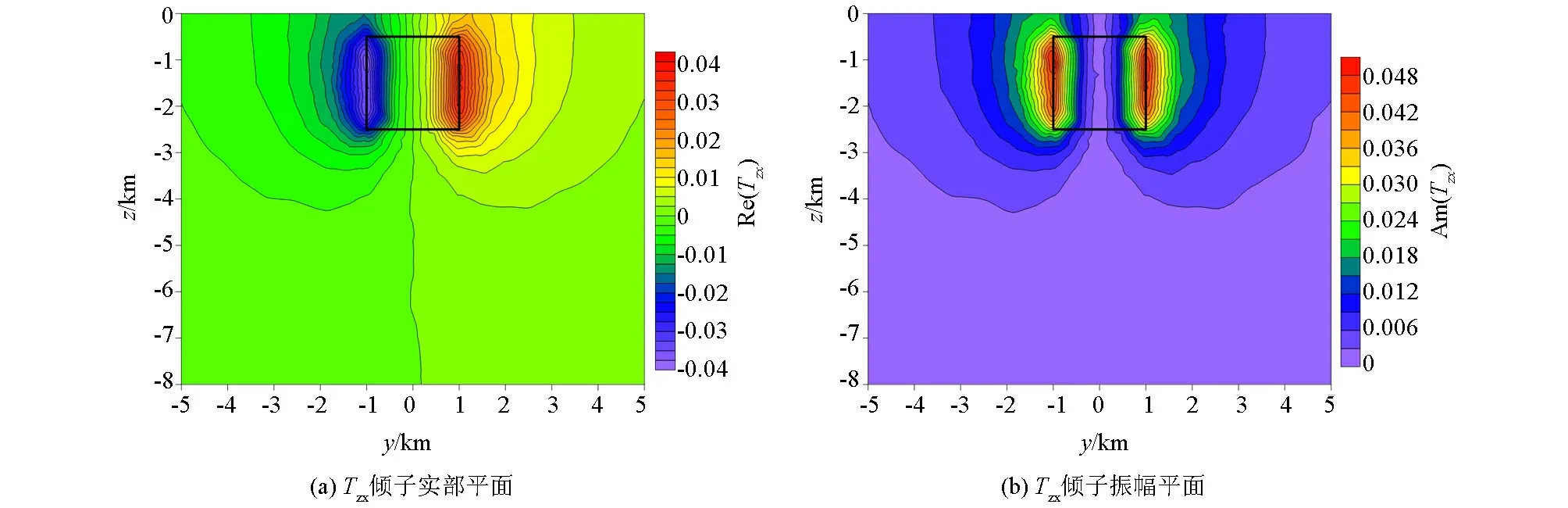
图4 低阻异常体模型倾子响应在F=0.1 Hz的YZ平面的切片Fig.4 Section diagram of low resistivity abnormal body model with tipper response in the YZ plane at F=0.1 Hz

2.2 左右组合异常体模型

在单个低阻异常体模型基础上增加一个大小埋深均不相同的高阻异常体，分别分布在左右两侧形成左右组合异常体模型，两异常体相距1 km，在XY、XZ、YZ平面的示意图如图5所示。异常体A为低阻异常体，电阻率为10 Ω·m，尺寸为1 km×2 km×2 km，顶面埋深为500 m；异常体B为高阻异常体，电阻率为1 000 Ω·m，尺寸为1.4 km×3 km×2 km，顶面埋深为1 000 m，围岩电阻率为100 Ω·m。

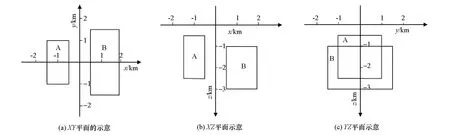
图5 三维左右组合异常体模型在不同平面的示意Fig.5 Different planes of three-dimension left and right combination abnormal body model

图6、图7、图8分别为频率为0.1 Hz的组合异常体模型的三维倾子响应在XY、XZ、YZ平面的切片图，分别给出了Tzx和Tzy的实部、虚部和振幅平面图。图中黑色矩形分别为A、B异常体在不同平面的投影，从切片图中可以看出倾子响应的虚部和实部的异常形态基本一致，虚部响应异常值较实部响应异常值偏小。在XY平面切面图中，Tzx响应在异常体A、B的上下边界处均表现为最大值或最小值，而Tzy只反映出了低阻异常体A的存在，没有反映出高阻异常体B的边界位置，可见倾子资料对低阻异常体的分辨率要好于高阻异常体。其中低阻异常体A的尺寸小于高阻异常体B的尺寸，则图中异常体A所对应的倾子响应的异常幅值范围小于B所对应的倾子响应异常幅值范围，表明异常体的大小对倾子响应的异常区域有影响，当异常体越大，倾子响应异常值幅值范围则越大。结合Tzx和Tzy可以较好地识别出低阻异常体A的中心位置以及4个边界的位置，无法准确判断高阻异常体的左右边界位置，且在XY平面Tzx比Tzy对异常体空间位置的反映效果要好。在XZ平面切片图中，同样对低阻异常体A分辨率较高阻异常体B的高，其中倾子响应异常值区域与低阻异常体A的范围一致，由此可以判断出异常体A的边界及埋深。从YZ切片图中可以看出，Tzx倾子异常值的实部与振幅值均关于Y=0轴对称，表明异常体的空间位置关于Y=0对称，由于高阻异常体的干扰，倾子响应曲线形态较乱受干扰严重，无法准确的判断出异常体A、B的边界。

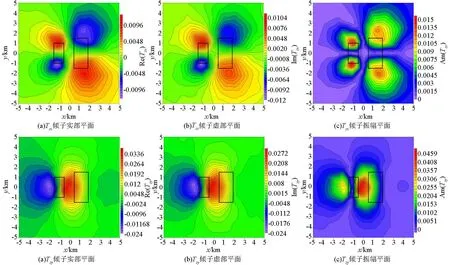
图6 左右组合异常体模型倾子响应在F=0.1 Hz的XY平面的切片Fig.6 Section diagram of left and right combination abnormal body model with tipper response in the XY plane at F=0.1 Hz

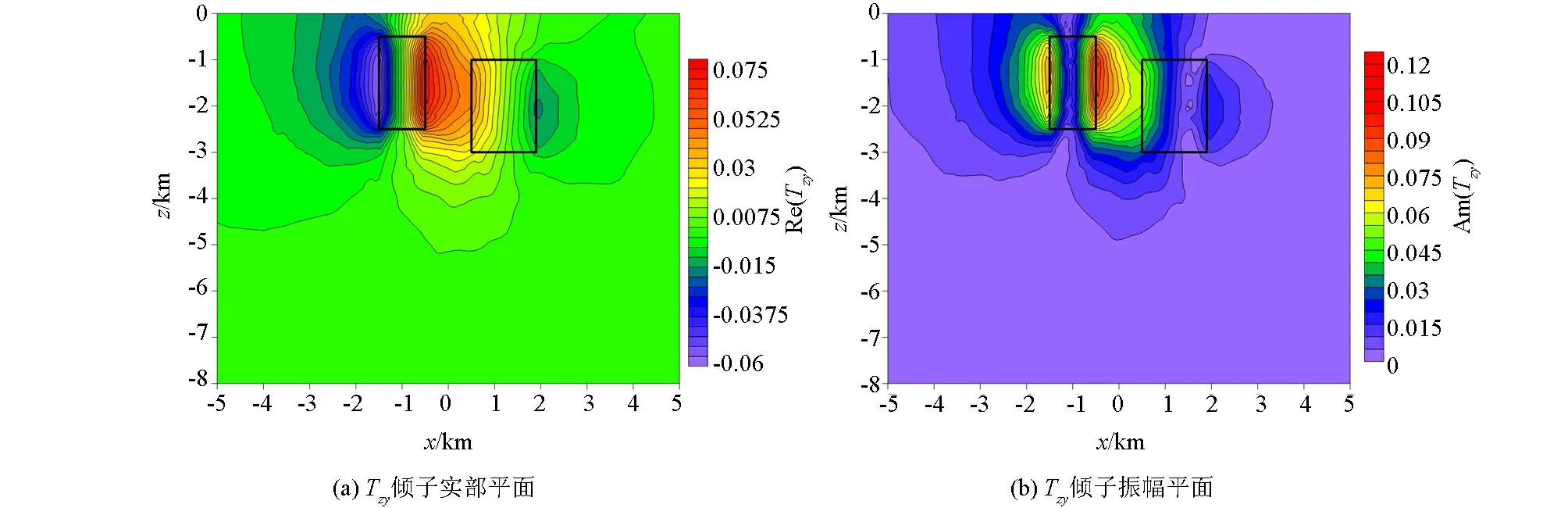
图7 左右组合异常体模型倾子响应在F=0.1 Hz的XZ平面的切片Fig.7 Section diagram of left and right combination abnormal body model with tipper response in the XZ plane at F=0.1 Hz

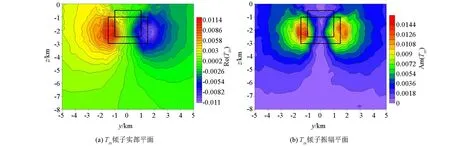
图8 左右组合异常体模型倾子响应在F=0.1 Hz的YZ平面的切片Fig.8 Section diagram of left and right combination abnormal body model with tipper response in the YZ plane at F=0.1 Hz

2.3 上下组合异常体模型

三维上下组合异常体模型在XY、XZ、YZ平面的示意图如图9所示，在电阻率为100 Ω·m的围岩中存在上下两个异常体A、B，在XY平面两异常体的中心与坐标中心一致，异常体A的尺寸为1 km×2 km×1 km，顶面埋深500 m；异常体B的尺寸为2 km×3 km×1 km，顶面埋深为2 500 m，两异常体A、B垂直相距1 km。设置异常体A、B的电阻率，使模型呈现上高下低或上低下高的电阻率模式。当异常体A的电阻率为10 Ω·m时，B的电阻率为1 000 Ω·m，当A的电阻率为1 000 Ω·m时，B的电阻率为10 Ω·m。分别进行正演模拟计算倾子响应值，对比分析不同电阻率模式下倾子响应特征。

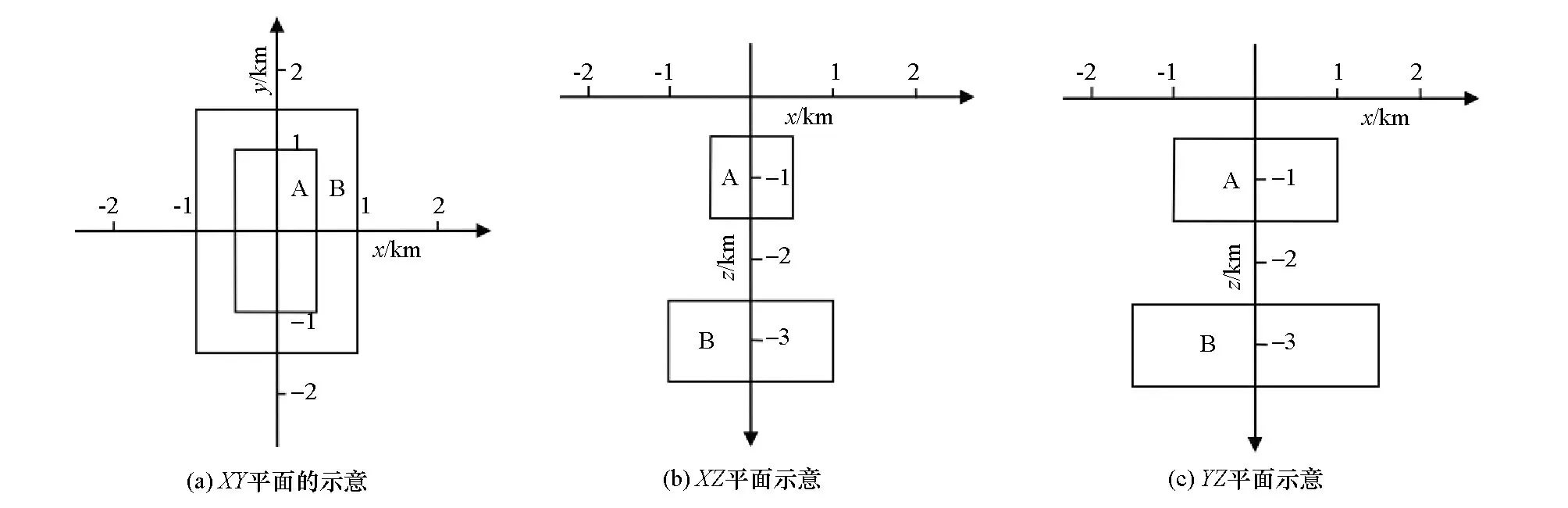
图9 三维上下组合异常体模型在不同平面的示意Fig.9 Different planes of three-dimension upper and lower combination abnormal body model

图10、图11、图12分别为上下组合异常体模型在电阻率上低下高和上高下低模式下的倾子响应在XY、XZ、YZ平面的切片图，计算频率为0.1 Hz，其中均为倾子实部响应值。图10a、c为上低下高电阻率模式下的Tzx和Tzy的实部平面图，图10b、d为上高下低电阻率模式下的Tzx和Tzy的实部平面图，对比不同模式下的Tzx实部响应特征，可以看出异常体A、B在XY平面的中心位于倾子实部的两异常区域的接触带之间，其中图10a只反映出了低阻异常体信息，且在低阻异常体的上下边界处倾子响应表现为最大值和最小值，而对于高阻异常体的特征没有反映出来，图10b则将高阻和低阻异常体的特征均反映的比较明显，对于高阻异常体的边界反映的比较准确，而低阻异常体的边界没有反映出来。同样对比图10c、d不同模式下的Tzy实部平面图，图10c只反映出了低阻异常体的左右边界，图10d则将高阻和低阻异常体的信息都反映了出来，且对高阻异常体的左右边界反映较准确。由此可知，倾子资料对低阻异常体反映较敏感，低阻异常体对高阻异常体存在屏蔽作用。从图11、图12中可以看出，均能反映出上下两个异常体，且异常体的左右边界均位于倾子最大值或最小值处，当异常体在X方向的尺寸相对较大时，所对应的倾子响应的最值距离也相应较大，与异常体边界对应较好，且在低阻异常体边界周围，等值线较密集，幅值也为最大，表明倾子资料对低阻异常体较高阻异常体敏感。

图10 上下组合异常体模型倾子响应在F=0.1 Hz的XY平面的切片Fig.10 Section diagram of upper and lower combination abnormal body model with tipper response in the XY plane at F=0.1 Hz

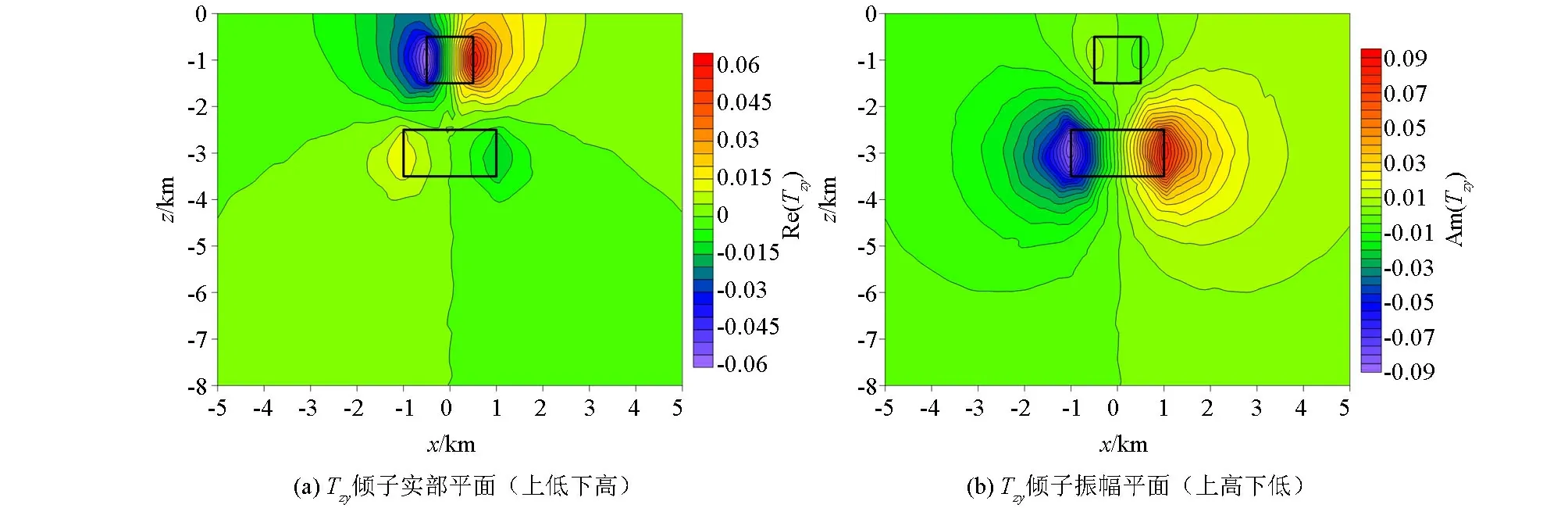
图11 下组合异常体模型倾子响应在F=0.1 Hz的XZ平面的切片Fig.11 Section diagram of upper and lower combination abnormal body model with tipper response in the XZ plane at F=0.1 Hz

图12 上下组合异常体模型倾子响应在F=0.1 Hz的YZ平面的切片Fig.12 Section diagram of upper and lower combination abnormal body model with tipper response in the YZ plane at F=0.1 Hz

3 结论

通过对多个复杂异常体模型下的倾子三维正演模拟计算，分析对比倾子资料的响应特征和规律，得出以下结论：

1) 倾子实部、虚部以及振幅值均能反映出异常体的空间分布位置、大小、埋深等，且异常体的边界一般位于倾子响应平面图中的最大值和最小值处，根据倾子资料在不同平面的切片图，能判断出该异常体在不同平面的投影大小及位置，从而判断出三维异常体的空间分布情况。

2) 倾子资料对低阻异常体的分辨率要比高阻异常体好，且低阻异常体的倾子响应值大于高阻异常体的响应值，低阻异常体对高阻异常体存在屏蔽作用。

3) 倾子资料可以很好地反映地电构造的水平非均匀性，可以利用倾子资料判断断裂构造的位置以及反映地下介质的不均匀性。

4) 倾子响应值都比较小，在实际采集过程中很容易受到环境的干扰，如何提高倾子资料的信噪比显得尤为重要。