基于KICA属性优化的支持向量机储层参数预测
王 维 强
(1.自然资源部 地热与干热岩勘查开发技术创新中心,河北 石家庄 050061; 2.中国地质科学院 水文地质环境地质研究所,河北 石家庄 050061)
0 引言
在油气勘探开发中,利用地震和测井资料对储层参数进行准确预测是非常关键的。人工产生的地震波通过地下传播,且在地面接收的地震数据中包含了油气储层的物性参数、流体性质等特征信息,将地震数据中的这些特征信息通过地震属性提取出来,并通过数学或统计学方法,计算出两者之间存在的线性或非线性关系[1],为储层预测与评价提供科学依据。由于地震属性的种类繁多,需要通过属性优化技术优选出尽可能少的对储层岩性及储层参数最敏感的属性组合[2]。目前的属性优化技术[3-5]主要包括主成分分析法、综合参数法、独立分量分析法(ICA)等。其中,在ICA理论基础上发展出一种新的非线性结构的核独立分量分析(KICA)技术[6],该技术构建了一种非线性函数空间,并在非线性函数空间中利用Mercer再生核方法,能从高斯及非高斯混合信号中提取出反映独立源信息的高阶统计特性信息,故利用KICA技术,能从大量的属性数据中有效提取出与储层物性参数、流体性质等相关的特征源信息。
目前常利用逐步回归分析、移动平滑法、灰色系统模型法、神经网络、支持向量机等技术[7],将地震属性及测井数据作为输入,对储层参数进行预测与评价。其中,支持向量机技术能够克服其他方法对于样本数目的限制,对于样本数目少、多维度、局部最小的非线性及线性系统均能很好适应。因此,本文综合两者的优点,通过KICA技术优选出与储层参数最敏感的属性组合,并利用少量已知井资料,通过支持向量机技术预测出整个研究区的储层参数特征。
1 方法原理
1.1 核独立分量分析技术
ICA技术[8]能从独立源信号线性混合的多维观测信号中分离出源信号,该技术利用线性变换后的非高斯型最大化来实现盲源分离,数学模型为x=As,其中x是观测向量,A是一个非奇异的混合矩阵,s是N维的源信号。ICA技术要解决的问题是寻找潜在分离矩阵B,该分离矩阵通过关系y=Bx,使得估计出的信号之间相互统计独立最大化,其中y为源信号s的最优估计[9]。
ICA技术是一种线性变换技术,且使用前提是混合信号中最多包含一个高斯分布的源信号,因此在该技术基础上,发展了KICA技术,该技术通过构建一个非线性函数空间,并使用Mercer再生核方法[10],不仅能够适应高斯及非高斯分布等多种信号混合情况,而且能够更好地适用于复杂的非线性结构的盲源分离。以下为KICA技术的基本思路[11]:
1)输入原始m维数据信号t1,t2,…,tm,并给出核函数k(t,s);
2)对输入的信号做均值化及球化处理;
3)求出初始独立分量s1,s2,…,sn的Gram核矩阵,且si=Kti;
4)定义γ(G1,G2,…,Gm)为下列方程的最大特征值:
(1)

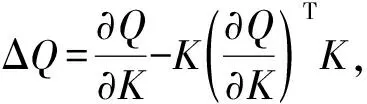
1.2 最小二乘支持向量机技术
支持向量机基于统计学理论——VC维理论[12],该技术还采用了结构风险最小化原则[13],能够不受神经网络对于样本数目的约束,对于样本数目少、多维度、局部最小的非线性及线性系统均能很好适应,下面对最小二乘支持向量机(LS_SVM)技术的基本原理介绍如下。
假设输入数据{(ui,pi)|ui∈Rn,pi∈Rn,i=1,2,…,n}。通过φ(u)将输入数据转换为高维特征空间,然后在高维特征空间设置如下函数:
p=wTφ(u)+h,
(2)
利用结构风险最小化原则,通过引进松弛变量ei,得出优化等式,最后通过相匹配的拉格朗日函数,对其求最小值,得出如下线性方程组:
(3)
式中:p=[p1…pn]T;In∈RN;Ω=K(ui,uj),为核函数。从而LS_SVM的估计函数为:
(4)
1.3 基于地震属性优化的储层参数预测实现原理
研究表明地下储层结构及构造、储层流体及参数等特征可作为盲源分离的独立源信号,由地面接收的地震信号中的振幅、相位、频率等属性信息就是这些独立源信号的线性或非线性组合。基于上述前提,本文储层参数预测技术的实现原理如下:提取与目标储层可能相关的沿层地震属性集,将地震属性集与储层参数进行相关性分析,去除冗余的地震属性;再利用极差标准化技术对地震属性数据作标准化处理,利用中值滤波技术去除地震属性数据中的异常噪声,利用主成分分析法对地震属性数据进行降维处理,分离出地震属性集的几个主成分,进一步去除属性间冗余相关的部分,最后利用ICA及KICA技术对降维后的地震属性进行属性优化,提取出相互统计独立的与储层物性参数、流体性质等相关的特征源信息,为下一步储层参数预测提供有效的属性体集合。
经ICA及KICA属性优化后的数据体与储层参数存在直接的复杂关系[14],可利用机器学习算法,再结合工作区已有的石油井中的储层物性信息,建立二者之间的定量关系,进而预测出整个工作区的储层物性参数特征。本研究分别通过径向基神经网络与最小二乘支持向量机经过模型试算及实例分析进行储层预测研究。图1为基于地震属性的储层参数预测技术流程(预处理中的属性压缩采用主成分分析法)。
2 模型试算
图2为一个储层厚度和速度参数在横向上变化的丘状体地质模型。图3为该丘状体模型的正演地震记录(共计200道)。首先进行属性提取工作,提取出与丘状体储层参数(厚度、速度)最相关的地震属性集合(对属性经相关性分析后,初步确定6种地震属性),主要包括:反射强度属性、L2模、自相关函数主瓣面积之比属性、波形正半周面积、均方根振幅属性、全谱平均频率属性。然后对该属性集做预处理工作:分别利用极差规范化及主成分分析进行数据标准化及数据降维。再通过ICA与KICA对降维后的属性体开展属性优化,以得到直接反映储层的独立源信息。

图2 丘状体地质模型 图3 丘状体地质模型的合成地震记录 Fig.2 Geological model of domal bodies Fig.3 Synthetic seismogram of domal bodies
将先验信息即储层厚度、速度及ICA与KICA优化后的属性体作为学习样本,其中储层厚度的学习样本采用地震记录第1、21、41、61、81、101、121、141、161、181、200道处的厚度样本分别为132.45、145.65、174.85、212.1、242.45、280、277.4、229.5、178.25、126、92.45 m,对应的速度样本分别为5 300、5 300、5 300、5 300、5 000、5 000、5 000、5 400、5 400、5 600、5 600 m/s,优化后得到两组优化属性作为地震属性学习样本,分别为[0.0735、-0.2355、-0.5382、-0.8533、-1.2067、-1.5378、-1.8762、-2.2171、-2.5824、-3.0326、-3.2275],[-1.9519、-2.7686、-3.7203、-4.4063、-4.2635、-4.6002、-4.7815、-4.9069、-4.5093、-2.2766、-1.8109],优化后的属性无具体量纲。
分别利用径向基神经网络及最小二乘支持向量机技术,学习出属性数据与储层参数之间的非线性关系,最终预测出整个研究区的储层厚度与速度的分布情况,如图4、5、6、7所示。

图4 经ICA属性优化及神经网络预测的储层厚度(a)与速度(b)Fig.4 Prediction of reservoir thickness(a) and velocity(b) based on ICA attribute optimization and neural network
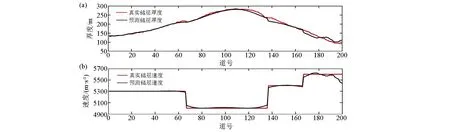
图5 经KICA属性优化及神经网络预测的储层厚度(a)与速度(b)Fig.5 Prediction of reservoir thickness(a) and velocity(b) based on KICA attribute optimization and neural network

图6 经ICA属性优化及支持向量机预测的储层厚度(a)与速度(b)Fig.6 Prediction of reservoir thickness(a) and velocity(b) based on ICA attribute optimization and SVM

图7 经KICA属性优化及支持向量机预测的储层厚度(a)与速度(b)Fig.7 Prediction of reservoir thickness(a) and velocity(b) based on KICA attribute optimization and SVM
通过模型试算得出,本研究中的属性优化技术及机器算法均能较好地拟合出储层的厚度、速度参数。其中,对于属性优化技术,KICA要好于ICA的最终储层速度与厚度拟合精度;对于储层参数预测的机器算法,最小二乘支持向量机要优于神经网络的储层速度与厚度拟合精度;且经KICA属性优化及最小二乘支持向量机拟合精度最高,符合预期效果。同时, 支持向量机基于统计学的VC维理论,且采用结构风险最小化原则 ,不受神经网络对于样本数目的约束,适用于已知资料较少的区域,下节将通过实例以验证其实际应用效果。
3 实例分析
运用属性优化的LS_SVM方法对某研究区侏罗系的地震资料开展了储层孔隙度参数预测。研究区位于阶梯状断裂的构造带上,油气藏类型为侏罗系礁滩型油气藏(以气藏为主),目的层主要为碳酸盐岩(以生物礁灰岩为主),该储层的储集性能好,灰岩骨架空隙、颗粒溶孔发育,且储层的厚度普遍发育较厚,由于储层的速度与孔隙度之间存在直接的联系,因此,利用本研究的储层参数预测技术来预测储层的孔隙度。
首先沿该目的储层提取与孔隙度相关的地震属性共计6个,具体为均方根振幅属性、平均反射强度属性、主频、全谱平均频率属性、平均瞬时频率属性、能量半时属性。然后对提取的属性进行预处理,分别对属性利用极差规范化及主成分分析进行数据标准化及数据降维处理,降维后属性体为3个,对降维后的属性体通过属性优化技术提取出直接反映地下储层特征的独立源信息。优化后得出3个属性分量,文中只显示其中有意义的2个分量,再根据已知地质资料,通过优化后的属性帮助解释人员进行生物礁储层预测工作(如图8、9所示),属性分量1反映的是生物礁灰岩储层特征,属性分量2反映的是非礁体储层特征。对比结果可见,两种属性优化方法得出的分量1都较好地反映出了生物礁储层的展布特征,且KICA属性优化结果对生物礁的展布更加清晰、准确,经ICA属性优化的储层特征中并没有预测出23井周围的生物礁体,而经KICA属性优化的储层特征中,不仅清楚反映出23井处的生物礁体形态特征,而且也精确且更加细致地预测出了21井、22井周围的生物礁储层展布特征。
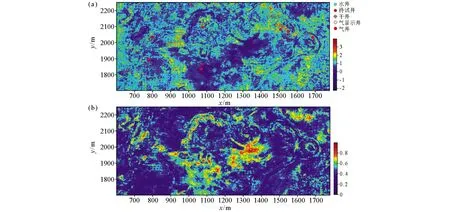
a—属性分量1;b—属性分量2a—attribute component 1;b—attribute component 2图8 经ICA属性优化的储层特征Fig.8 Reservoir characteristics optimized by ICA attributes

a—属性分量1;b—属性分量2a—attribute component 1;b—attribute component 2图9 经KICA属性优化的储层特征Fig.9 Reservoir characteristics optimized by KICA attributes
表1为研究区中已知的10口井中目的层处的平均孔隙度值。通过已知孔隙度及相应井旁道处优化的地震属性,利用机器学习技术,建立优化属性体及孔隙度之间的定量关系,并利用该关系对全区进行平均孔隙度预测。然而研究区中已知井数量有限,这里将III-1及21号作为验证井,其他井为学习井。最终储层平均孔隙度预测情况如表2所示。

表1 已知井位的孔隙度值

表2 平均孔隙度预测结果
从平均孔隙度预测结果可以看出,由于井的数量太少,神经网络预测的误差较大。而LS_SVM技术则具有较高预测精度,表明LS_SVM技术能够解决少井的情况,神经网络技术则依赖于足够的训练井,否则会造成较大的误差。
图10、11为不同方法预测的整个研究区内平均孔隙度分布情况,可以看出,几种方法均能较好显示储层的孔隙度分布情况,其中基于KICA属性优化的LS_SVM预测的结果对孔隙度分布的描述更加细致、准确,而神经网络方法由于训练井数目少的问题,其预测结果变化范围大,表现出较大的误差。

图10 基于ICA优化的神经网络孔隙度预测结果Fig.10 Porosity prediction based on ICA optimization and neural network
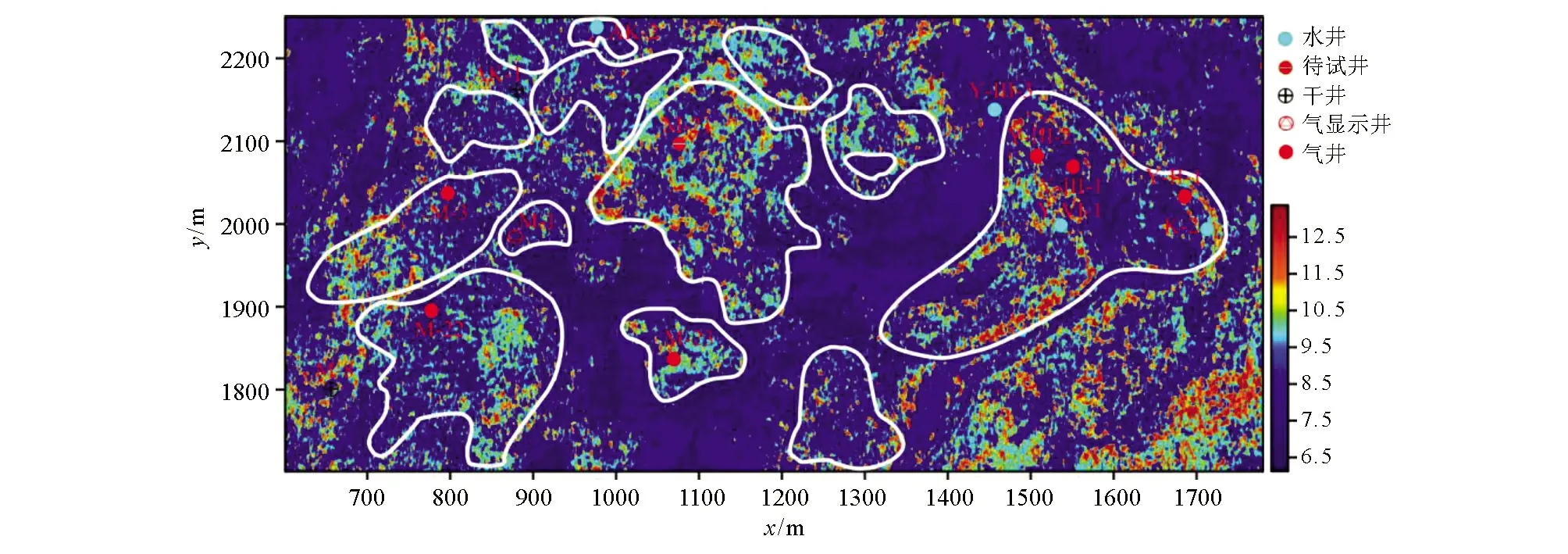
图11 基于KICA优化的支持向量机孔隙度预测结果Fig.11 Porosity prediction based on KICA optimization and SVM
4 结论
本文主要研究了经属性优化的机器学习储层参数预测技术,经过模型仿真与实例验证,对ICA与KICA属性优化技术、神经网络与LS_SVM储层参数预测技术进行了系统研究,得出如下结论:
1)在礁滩型等海相碳酸盐岩储层预测中,KICA及ICA属性优化均取得了较好的储层预测效果,而KICA技术对礁滩型储层特征展布更加清晰、准确,因此这种基于核函数的非线性回归方法适用于复杂的海相碳酸盐岩储层预测工作,效果远好于线性方法,同时要注意核函数的选取,不同目标储层要选择不同的核函数进行效果对比以寻求最优解。
2)最小二乘支持向量机储层参数预测的泛化性要好于神经网络类算法,能够较好地解决训练样本数据较少的问题,预测精度较高,在地震勘探中具有重要的实用意义,其中核函数的选取对其泛化性具有较大影响,可作为下一步研究的方向。
——北美又一种非常规储层类型

