果园行间3D LiDAR导航方法

刘伟洪，何雄奎,3,4※，刘亚佳,3,4，武志明， 袁常健，刘理民，齐 鹏，李 天

（1. 中国农业大学药械与施药技术研究中心，北京 100193；2. 中国农业大学工学院，北京 100083；3. 中国农业大学理学院，北京 100193；4. 中国农业大学农业无人机系统研究院，北京 100193；5. 山西农业大学农业工程学院，太谷 030801）

0 引言

中国的水果种植面积与产量均居世界第一，然而落后的果园机械化水平无法满足当下的水果产业需求。为了促进水果产业的绿色无公害、标准化与产业化的进程，提高农业劳动的生产效率和农产品商品率，保持水果生产质量的稳定性，提高我国水果生产的机械化与自动化成为亟待解决的问题[1-2]。果园机械自主导航技术是实现果园作业机械化、自动化、管理精细化的关键，也是实现果园精准施药作业中人机分离的基础[3]，相比于传统的人工驾驶，该方法能够有效解决水果生产中人力缺乏、劳动强度大等问题[4-8]。

目前，国内外针对果园导航方面的研究方法主要有全球卫星导航系统（Global Navigation of Satellite System，GNSS）、机器视觉导航、多传感器融合导航以及激光导航等[4,9-13]。郭成洋等[14]设计了一种基于RTK-BDS的自动导航控制系统，利用卡尔曼滤波技术提高了该系统在果园中的定位精度，并在农用车辆上进行了直线跟踪试验，在0.5 m/s的速度下，最大横向偏差不大于0.086 m，平均偏差不大于0.036 m。Li等[15]基于低成本双目视觉实现了丘陵地区野外山区道路3D自主导航线的提取，并分别在直路、多曲率复杂道路和起伏道路上进行了试验，拟合的导航线与真实中线间最大偏差分别为0.133、0.195和0.216 m。彭顺正等[16]针对复杂的矮化密植枣园，提出一种基于图像处理的枣园导航基准线生成算法，通过对多种天气与噪声多元叠加等条件进行试验，视频检测结果表明，单一工况条件下算法动态检测准确率达81.3%以上，每帧图像处理平均耗时低于1.7 s。Bayar等[17]通过融合平面激光扫描仪、里程计和转向编码器的数据实现了机具在果园中的自动导航，并通过李雅普诺夫（Lyapunov）函数证明了所设计的控制器的稳定性。

激光导航，主要借助激光测距（Light Detecting and Ranging，LiDAR）传感器对周围的环境进行实时感知，相比于传统的图像传感器，LiDAR传感器具有测距精度高、主动发光，受光线影响小等优点[18-20]。常见的基于LiDAR的导航主要包括平面激光扫描仪（Planer Laser，PL），通过PL对周围环境进行感知，提取树干的位置信息，进而实现作业机具的自主定位[21]。Zhang等[22]通过考虑标准化果园中的株距、行距和树干直径等农艺要求，建立了不同的过滤阈值以消除PL点云数据的离散点，有效提高了果园环境下自动导航的精度，实现了果园机具的自主运行。薛金林等[23]以农业机器人为平台，基于LMS291-05激光扫描仪研究了果园单侧存在行缺失情况下机器人的导航性能，试验分别在行距不均的冬青树与梨树中进行，在冬青树间的最大横向偏差为17.5 cm，梨树间为28 cm。牛润新等[20]通过二维激光雷达采集果园原始点云数据，经过预处理、自适应设定聚类阈值、二次曲线拟合、干扰剔除等步骤有效降低丘陵山区果园中的斜坡及杂草对果树树干检测精度的影响，综合树干检测试验得到95.5%的平均准确率。周俊等[24]以密植果园为研究对象，针对GNSS在导航中卫星信号被遮挡，单纯的里程计存在累计误差等问题，首先以激光雷达扫描树行并使用圆弧聚类检测树干中心点，然后记录在世界坐标系中，导航作业时再次扫描树行寻找树干中心点并同先前记录在世界坐标系下的树干中心点进行匹配，利用匹配结果矫正里程计计算出机器人的位置和航向，10次重复试验表明，该方法在世界坐标系x和y方向的定位误差标准差均为8 cm。

基于二维激光扫描仪的方法能够很好地适应树干明显、管理相对规则的果园，然而对于树冠茂密、树干被遮挡、树枝相连成片等复杂三维果园环境，二维激光雷达无法很好表征其三维场景特征，所提取的用于导航的信息容易受到较大的干扰[25]。因此，本文提出一种基于3D LiDAR的果园树行识别与导航线拟合的方法，使用直通滤波算法缩小兴趣区域（Region of Interest，ROI），提出挖空算法应对树枝相连成片，根据果树在竖直方向满足轴对称的分布特征，提出一种体心等效树干位置的方法；分别使用随机采样一致性（Random Sampling Consensus，RANSAC）算法与最小二乘法（Least Square Method，LSM）对机具左右树行所在直线进行拟合；为了提升系统的鲁棒性与容错性，基于左右树行平行的假设，提出一种基于平行度的互补融合（Complementary Fusion, CF）策略实现RANSAC与LSM拟合结果的互补融合，并求其中线作为目标导航线；基于移动机器人的差速运动学模型，对纯跟踪算法进行改进，实现机器人对树行的跟踪。

1 导航系统

1.1 硬件组成

系统主要由3D LiDAR（中国北科天绘公司R-Fans-16）、 RTK GNSS定位系统（中国华测导航公司P3-DU）、装有Ubuntu18.04操作系统的工控机（处理器i7 10510U）和移动机器人（中国松灵机器人公司Scout-Mini）组成。

3D LiDAR为一款16线机械激光雷达，安装在移动机器人正前方，距离地面垂直高度为0.50 m，其水平视场角为360°，在帧频率为5～20 Hz时水平角分辨率为0.09°～0.36°，垂直视场角为±15°，垂直角分辨率为2°，点频率为320 kHz，最大测距为200 m，测距精度为2 cm；RTK GNSS定位系统在固定解下的水平定位精度为±1 cm，该系统主要用于记录机器人的实时轨迹，作为参考真值，对系统的定位与跟踪精度进行评价。

移动机器人为四轮驱动差速运动底盘，可直接通过CAN总线接收来自上位机的目标线速度v与目标角速度ω，实现任意转弯半径的轨迹跟踪。定义满足右手定则的机体坐标系{V}如下：以3D LiDAR中心为坐标原点o，x轴指向机器人的正前方，y轴平行于机器人的轮轴且指向左方，z轴垂直指向正上方，图1为系统的硬件平台与机体坐标系{V}。

1.2 软件组成

系统的软件模块框图如图2所示。

在第k帧下，LiDAR产生{V}下的原始三维点云数据集Pk，分别使用点云库（Point Cloud Library，PCL）[26]中的“PassThrough filter”与“VoxelGrid filter”进行ROI的裁剪与降采样得到数据集Qk；使用PCL中的欧式聚类算法对Qk进行聚类，同时求得每一类别的体心并将其投影至给定平面等效代替树干在{V}下的位置，得到数据集Ek；分别使用RANSAC与LSM算法对Ek进行拟合，得到左右树行在{V}下直线方程的表达式Ll-RANSAC、Lr-RANSAC、Ll-LSM、Lr-LSM；基于余弦定理提出一种两直线间的平行度计算方法，得到4组表示平行度的余弦值与最佳余弦值cos(α0)、cos(α1)、cos(α2)、cos(α3)与cos(αbest)；根据4组余弦值与最佳余弦值对Ll-RANSAC、Lr-RANSAC、Ll-LSM、Lr-LSM进行互补融合，得到最终的左右树行直线方程Lfit-l、Lfit-r，计算左右树行的中线得到目标导航线Lfit-nav；对纯跟踪算法（Pure Pursuit）进行改进，分别输出目标线速度（v）、目标角速度（ω），用于控制移动机器人跟踪目标轨迹。

2 导航方法

2.1 果树定位

使用PCL中的直通滤波函数“PassThrough filter”对Pk进行x、y、z三个维度的裁剪滤波以提取合适的ROI。设定成员函数“setFilterLimits()”中x轴方向的2个阈值参数为（-2dtre，5dtre），y轴方向为（-1.25drow，1.25drow），z轴方向为（-0.8hlidar，htre），其中drow为行距（4 m），dtre为株距（1.5 m），hlidar为3D LiDAR中心距离地面的高度（0.5 m），htre为树高（4 m），将成员函数“setFilterLimitsNegative()”设置为“假”用于舍弃局外点而保留局内点，将该算法处理后的点云保存至Pk'中，ROI选择如图3a所示。

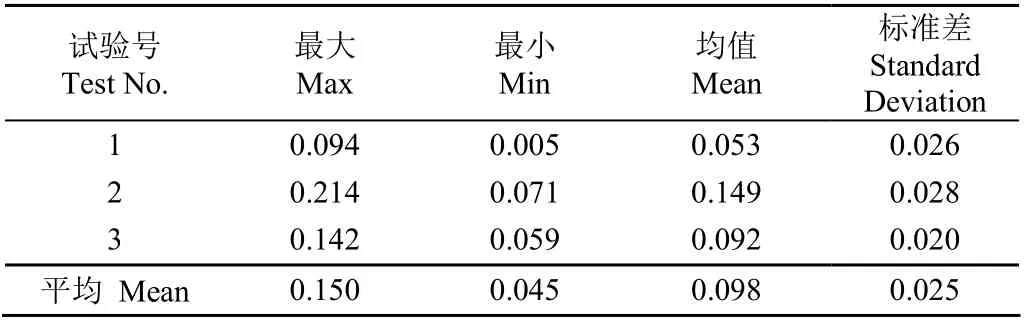
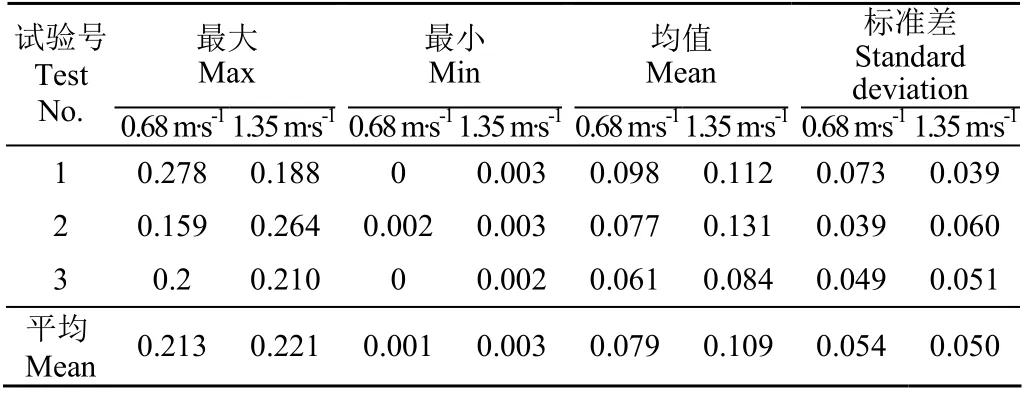
对于果树枝条相连成片，造成无法识别单棵果树的情况，基于PCL中的“PassThrough filter”函数提出一种挖空算法，对Pk'进行挖空、打断。提前设定并初始化x轴上的2个边界值xn、xp以及平移距离Δd，并定义中间变量xn′、xp′。当满足条件xn′

为降低后续处理的计算量，使用PCL中的“VoxelGrid filter”对点云集Pk″进行降采样。设置体素尺寸为（0.08, 0.08, 0.08），即将边长为0.08 m的立方体内的点等效成一个点，将滤波结果存放在Qk中。

为实现果树识别，使用PCL中的欧式聚类算法对经过稀疏处理的点云Qk进行聚类。由于距离传感器较近的果树点云较密（通常不超过5 000个），距离传感器较远的果树点云较为稀疏（通常不少于12个），为保证感知范围内的果树被准确识别，将该算法的主要参数聚类目标点云设置为Qk、最小距离阈值设置为dtre/3、聚类点的最小数目设置为12、最大数目设置为5 000。为求得每一棵果树在{V}下的位置，根据理想果树树形分布满足中间集中、周围发散，且从其正视图可以看出树冠呈轴对称[25]分布的特点，使用该截面的几何中心等效代替树干的中心Otre（图3b），将第k帧下第i棵果树的体心记为itreO，其具体求解方法如下：首先求解聚类后第i棵果树点云集沿x、y、z轴向的最值坐标(xmax,xmin,ymax,ymin,zmax,zmin)，然后根据式（4）～（6）分别求解3个轴向最值坐标的中点，得到该果树的体心位置坐标。由于果园导航主要关注果树相对于移动机器人的平面位置，因此，令式（6）为0得到式（7），将三维体心投影至二维平面，得到最终体心，将第k帧下的所有果树的体心itreO组成的集合记为Ek，如式（8）所示。

2.2 导航线拟合

以x轴为中线，将2.1节中求得的点云集Ek分成左右2个组Ek-l与Ek-r且满足式（9）。使用RANSAC算法[26-27]分别对点集Ek-l、Ek-r进行拟合，结果分别表示为式（10）、（11），使用LSM算法[28]分别对点集Ek-l、Ek-r进行拟合，结果分别表示为式（12）、（13）。

RANSAC具有较强的抗干扰能力，能够在样本数据较少时有效排除局外点的干扰，LSM在给出的所有点中进行权衡，取综合最优，数据点较多时，结果较好，但在样本数据集较少时容易受到局外点的干扰[29-30]。可见在样本数据较少时，二者的拟合结果刚好互补，同时基于实际果园左右树行平行的假设，取得最佳拟合结果的条件为左右树行存在最佳平行度，故可使用平行度对2种算法的拟合结果进行互补融合。图4为平行度定义，在{V}下，存在2条直线Ll、Lr，且与y轴分别交于点B、C，于无穷远处交于点A，由此得到△ABC，点A、B、C分别对应边a、b、c，点A所对应夹角为α，角α的余弦值cos(α)如式（14）所示。当α趋于0时，cos(α)趋于1，其几何意义表示Ll与Lr的平行程度最高，故使用该值表示两直线的平行程度。鉴于实际情况下Ll、Lr的夹角不允许超过，故设定α取值区间为[0,]，则对应的cos(α)取值区间为[0,1]。

根据平行度将左右树行的不同表达式进行互补融合。由互补滤波原理[31]定义式（16）、（17）的2个互补融合参数coef0、coef1，根据式（18）～（21）可求得最终融合结果。根据式（14）分别计算4个平行度cos(α0)、cos(α1)、cos(α2)、cos(α3)，定义并计算式（15）所示的最佳平行度cos(αbest)，设定容忍阈值cos(αth)=0.95。当cos(αbest)>cos(αth)时，通过式（22）～（23）分4种情况对左右树行的表达式进行融合，否则执行式（24）～（25）舍弃当次融合并保留上次融合结果。4种情况具体为：1）当cos(αbest)=cos(α0)，执行式（18）和式（20）；2）当cos(αbest)=cos(α1)，执行式（18）和式（21）；3）当cos(αbest)=cos(α2)，执行式（19）～（20）；4）当cos(αbest)=cos(α3)，执行式（19）和式（21）。最后，根据式（26）求取左右树行的中线，得到目标导航线Lfit-nav。求解时，使用直线方程斜率k与截距b分别代替式（18）～（26）中相应的直线标识L，如由式（18）分别求得融合后的左树行的斜率fitlk-与截距fitlb-分别为式（27）～（28），同理可求得其他直线的具体参数。最终求得的左树行直线为式（29），右树行直线为式（30），拟合的导航线所在直线为式（31）。

2.3 树行跟踪

由于移动机器人为线控底盘，且满足差速运动学模型，故可直接接收来自上位机发送的线速度（v）与角速度（ω）指令，实现任意半径的轨迹跟踪。

图5为移动机器人轨迹跟踪示意图，结合纯跟踪算法[32]可知，在目标轨迹S上选择一个点P作为跟踪点，则机器人从当前位置到达点P的轨迹可以视为一段半径为R（m）的圆弧轨迹，对点P跟踪的关键在于对圆弧轨迹半径R的求解。在△EoP中，由正弦定理可得式（32），式中θ为航向偏差（rad），l为前视距离（m），进一步展开得到式（33），进而可以求出式（34）所示的跟踪轨迹半径R。过点P作PD垂直x轴于点D，在直角△oDP中，由正弦定理可得式（35），将其代入式（34）可得式（36）。

要控制移动机器人跟踪半径为R的圆弧轨迹，在线速度v给定的情况下，只需根据式（37）求出目标角速度ω，将式（36）代入式（37）得到式（38）。

由式（38）可以看出，ω与l成反比，当l越大，ω越小，调节越平稳，反之，越剧烈。在此，充分考虑前视距离与线速度的关系，并假设l与v满足线性关系，表示为式（39），式中K1为比例系数，e为初始前视距离（m），表示移动机器人在线速度为零时的前视距离。将式（39）代入式（38）得到式（40）。将航向偏差加以考虑，设定一个横向偏差阈值dth（m），当横向跟踪偏差达到该阈值以内时，在式（40）中加入航向偏差负反馈K2θ对横向调节加以抑制，提前对移动机器人的航向进行修正，防止移动机器人在横向偏差上调节过度进而造成反复调节，由此得到ω的表达式（41），由式（35）和式（39）求得式（42）的θ，将式（42）代入式（41）求得ω的最终表达式（43）。

将目标线速度v与目标角速度ω发送给线控底盘，即可实现对目标轨迹的跟踪。

3 试验结果与分析

3.1 定位试验

在中国农业大学校园内搭建了一个长8 m，宽4 m的人工篱壁式仿真果园，如图6a所示，为了排除试验的偶然因素，定位试验共进行3次重复。使用RTK定位系统建立仿真果园地图（包括左右树行与树行中心线），试验时遥控移动机器人沿仿真果园的中心线以0.33 m/s的速度匀速前进，同时运行本文所述的树行拟合算法，实时输出航向偏差与横向偏差。图6b为定位点云示意图，可以看出，树墙被挖空算法打断成多个立方体，RANSAC与LSM对立方体的体心的拟合结果几乎无差，CF融合后的树行也接近重合。图7a为RTK定位系统记录的3次试验的实时轨迹，可以看出实时轨迹均匀分布在真实树行的中心线附近。图7b为3种拟合算法与RTK输出的横向偏差对比典型结果，以第2次试验为例，可以看出，3种拟合算法输出的横向偏差与RTK输出的横向偏差真值变化趋势一致，RANSAC与LSM的偏差基本重合，CF的结果明显优于RANSAC与LSM。图7c为CF输出的横向定位偏差误差，表示3次试验中CF输出的横向偏差与RTK输出的横向偏差真值之间的误差，可以看出3次试验的最大误差不超过6.1 cm，满足果园导航作业的横向定位精度要求。

由于移动机器人沿着果园的中心线行走，故可将航向定位偏差的真值当作0，CF输出的结果就是真实的航向偏差。表1为CF输出的航向定位偏差统计结果，规定以导航线为基准线，机体坐标系的x轴与基准线逆时针所成夹角为正，顺时针所成夹角为负，可以看出，3次航向定位偏差正向最大均值为1.24°，负向最大均值为1.65°，平均偏差为0.84°，标准差均值为0.42°，基本满足果园作业航向定位要求。

表1 CF输出的航向定位偏差统计结果 Table 1 Heading positioning deviation statistical results of complementary fusion output (°)

表2为横向定位偏差统计结果，规定以导航线为基准线，移动机器人在基准线左侧的横向偏差记为负，移动机器人在基准线右侧的横向偏差记为正，可以看出，3次试验中，RANSAC与LSM输出的正向最大横向定位偏差均值均为0.052 m，负向最大横向定位偏差均值均为0.050 m，偏差均值均为0.028 m，标准差均值均为0.016 m，这主要是因为果园较为标准，RANSAC与LSM算法性能相当，导致拟合结果几乎没有什么差别；CF与RTK输出的正向最大横向定位偏差均值分别为0.034、0.036 m，负向最大横向定位偏差均值分别为0.044、0.039 m，偏差均值均为-0.028 m，标准差均值均为0.016 m，CF的输出结果与RTK输出的真值几乎相同，且CF的输出较RANSAC与LSM有所提高，说明互补融合算法具有一定的抗干扰能力。

表2 横向定位偏差统计结果 Table 2 Statistical results of lateral positioning deviation m

3.2 树行跟踪试验

3.2.1 篱壁式仿真果园树行跟踪

树行跟踪试验中K1=10，K2=-1，v=0.43 m/s，e=1.05 m，dth=0.08 m；同样进行3次重复。图8a为实时跟踪轨迹，可以看出，3次试验中移动机器人的实时轨迹有先靠近中心线，再远离中心线，最后又靠近中心线的趋势，这主要与树行跟踪控制器中的航向负反馈有关。图8b为RTK输出的横向偏差，可以看出，3次试验跟踪偏差都有先减小、后增大、再减小的调节趋势，符合图8a所记录的实时轨迹的变化趋势，以第2次试验（图中绿色曲线所示）为例进行说明。

移动机器人从0 s（对应横向偏差为-21.4 cm）出发向中心线靠近，横向偏差开始正向减小，至第4 s（对应横向偏差-12.73 cm）后，CF输出的横向偏差小于给定阈值dth（0.08 m），航向调节被引入，且航向调节作用大于横向调节，于是移动机器人开始背离中心线，横向偏差反向增大，至第10 s（对应横向偏差为-17.4 cm），CF输出的横向偏差超出给定阈值dth（0.08 m），横向调节作用大于航向调节作用，于是移动机器人又开始向中心线靠近，横向偏差逐渐减小，直至第15 s，横向偏差变为-7.1 cm，如果测试果园足够长，移动机器人将按照该规律反复调节，直至横向偏差与航向偏差均消失。跟踪试验证明本文所提出的导航线的拟合方法在篱壁式仿真果园中满足导航所需的定位精度，改进的纯跟踪控制算法能够控制移动机器人进行树行跟踪，且具有一定的航向调节作用，能够有效减少跟踪过程中的超调次数。

表3为RTK输出的绝对横向偏差统计结果，可以看出，3次跟踪试验的绝对最大横向偏差均值为0.150 m，绝对最小横向偏差均值为0.045 m，绝对偏差均值为0.098 m，绝对标准差均值为0.025 m。

表3 RTK输出的绝对横向偏差统计结果 Table 3 Absolute lateral deviation statistical results of RTK output m

3.2.2 梨园跟踪

为验证系统对真实复杂果园的适应性，在中国农业大学上庄试验站的梨园（N40°08′38.7276″，E116°11′30.4584″）进行了树行跟踪试验，试验场景如图9a所示，可以看出树行中间长有杂草，且路面不平整。图9a为真实梨园试验场景，该梨园行距为4 m，株距为1.5 m。随机选择一棵梨树进行物理尺寸测量，图9b为梨树尺寸标注，其主干为0.43 m，冠层高度为3.07 m，冠层下层厚度为2.7 m，冠层中层厚度为0.82 m。试验时随机选择梨园的一段，分别进行两个线速度的跟踪试验，每个试验进行3次重复，每次试验都从同一位置附近出发，并最终停在同一位置附近，单次试验所行走的路程约为27 m。在第一个线速度跟踪试验中，设定式（43）中K1=20，K2=-1，取v=0.68 m/s，e=1.05 m，dth=0.08 m；在第二个线速度跟踪试验中仅改变移动机器人的线速度，且取v=1.35 m/s，其他参数均不变。图9c为树干提取结果，可以看出相连成片的梨树墙被成功打断成若干立方块，且其体心在xoy平面上的坐标被等效为对应果树在{V}下的位置，有效克服了传统平面激光扫描仪只能获取树干信息实现果树定位的缺点。图9d为等效后的树干的实时拟合结果，其中红色直线为目标导航线。

图10a为梨园跟踪时RTK记录的实时轨迹，可以看出，在2个线速度的跟踪试验中，系统均能控制移动机器人在树行中心线附近跟随。图10b为RTK输出的横向偏差，当v=0.68 m/s时，3次重复试验中系统的横向跟踪偏差在27.8 cm以内，v=1.35 m/s时，3次重复试验中系统的横向跟踪偏差在26.4 cm以内。

表4为2个线速度下RTK输出的绝对横向偏差统计结果，可以看出，线速度为0.68 m/s时，系统的最大绝对横向偏差为21.3 cm，最小绝对横向偏差为0.1 cm，均值为7.9 cm，标准差为5.4 cm；线速度为1.35 m/s时，系统的最大绝对横向偏差为22.1 cm，最小绝对横向偏差为0.3 cm，均值为10.9 cm，标准差为5.0 cm。

表4 真实梨园树行跟踪绝对横向偏差统计结果 Table 4 Absolute lateral deviation statistical results of real Pear orchard’s tracking experiment m

2个不同线速度的树行跟踪，结果相差不大，但v=0.68 m/s的结果仍然略优于v=1.35 m/s，结合式（43）分析可知，在较低的线速度下，跟踪的前视距离更小，系统调节的次数更多，但过多的调节次数会降低系统的稳定性，这也正是v=1.35 m/s的标准差略优于v=0.68 m/s的原因，也进一步表明改进后的纯跟踪算法对不同线速度的跟踪具有一定的适应能力，系统的实时性能基本满足果园低速作业要求。该结果比篱壁式仿真果园跟踪试验中的结果略差，主要是因为真实梨园路面长有杂草且不平整、移动机器人重量较轻，容易产生滑移，同时由于梨树树冠并不呈理想的轴对称分布，导致系统的定位精度受到影响，从而造成移动机器人偏离中心线较大的距离。总体上，系统能够在梨园下实现较为精准的定位，并且能够控制移动机器人实现对梨园树行的跟踪。

4 结 论

本文针对平面激光扫描仪在果园导航中获取息量少，导致无法有效应对树冠茂密、树干被遮挡、树枝相连成片的复杂三维果园场景，提出一种基于3D LiDAR的果园行间导航方法，并分别在篱壁式仿真果园与梨园中进行了相关试验，主要结论如下：

1）以3D LiDAR为感知设备，通过直通滤波算法缩小导航所需ROI，使用欧式聚类方法找到ROI中的果树，并使用每棵果树的体心等效树干位置，基于平行度实现对RANSAC与LSM所拟合的左右树行的互补融合，并求其中心线得到目标导航线，考虑移动机器人的线速度与航向偏差的影响，对纯跟踪控制算法进行改进。

2）基于差速运动机器人验证了本导航系统的定位与跟踪性能。系统在篱壁式仿真果园中的航向定位偏差在1.65°以内，横向定位偏差在6.1 cm以内；绝对横向跟踪偏差在15 cm以内。

3）系统在梨园中以0.68 m/s的速度跟踪树行的最大绝对横向偏差不超过21.3 cm，以1.35 m/s的速度跟踪树行的最大绝对横向偏差不超过22.1 cm。表明本系统具有足够的定位精度与跟踪精度，可广泛用于标准果园与复杂三维果园机械的自主导航，具有可靠的稳定性。