收获机与运粮车纵向相对位置位速耦合协同控制方法与试验

张闻宇，张智刚，罗锡文，何 杰，胡 炼，岳斌斌

（华南农业大学南方农业机械与装备关键技术教育部重点实验室，广州 510642）

0 引言

为缓解农业劳动力短缺，降低农业劳动强度，全过程、全天候的无人化农场将成为未来农业的重要发展方向[1]。农业装备智能导航控制技术是无人农场的关键之一[2-6]，近年来研究者针对旱田[7-10]、水田[11-12]、鱼塘[13]等农业装备的智能控制技术进行了大量研究，同时研究了卫星[14-17]、激光雷达[18-19]或视觉[20-22]定位导航方法，取得良好的控制效果，但多数研究主要针对单机的自主控制。在无人农场收获环节中，由于收获机粮仓有限，需要收获机与运粮车的协同配合。其中将收获机的粮食转运到运粮车需要实现精准自主卸粮，研究收获机和运粮车相对位置协同控制方法对于实现无人农场全程自主收获具有重要意义。

国内外研究者对相对位置协同控制方法进行了相关研究。日本的Noguchi等[23]设计了基于Follow algorithm和滑模变控制方法的主从农机协同作业控制方法，速度设置在0.5～1.5 m/s之间，仿真试验结果表明双机协同的相对位置均方根误差为0.106 m。Zhang等[24]出于安全考虑设计了主从协同的控制算法，该算法包含状态反馈和扰动前馈的PD控制逻辑，构建了主从农机导航系统，田间协同导航试验结果表明，从机路径跟踪误差大多数时间在0.1 m以内。Zhang等[25]针对田间协同作业导航性对位置误差控制，设计了PD控制器，速度为0.83 m/s时，协同导航试验表明两机的相对位置平均偏差为0.13 m，方差为0.15 m。Luo等[26]在两辆电动机器人上验证了相对位置协同控制方法，主机速度为0.3 m/s，初始偏差为0.2 m时，相对位置平均误差为0.01 m，方差为0.03 m。白晓平等[27]针对联合收获机群协同导航作业提出一种基于领航-跟随结构的收获机群协同导航控制方法，用于控制路径跟踪横向偏差。许韶麟[28]采用预测模型方法实现了4架电动机器人的协同编队功能，停止后采用卷尺测量，误差不超过5 cm。邹存名等[29]基于线性矩阵不等式的模型预测控制器设计了电动机器人车队协同方法，基于Arduino控制单元搭建试验车队验证了算法的有效性和实用性。

上述研究针对多机器人相对位置协同问题提出了多种控制方法，多数研究以小型机器人为对象，控制对象的线性度较高，但控制方法的速度适应范围不能满足收获协同卸粮作业需求。本文拟针对自主收获精准协同卸粮作业的需求，分析纵向相对位置协同原理；建立相对位置几何模型；设计位速耦合纵向相对位置协同控制方法和辨识车速系统模型，建立仿真模型进行参数优化和对比试验研究；通过田间空载试验和实际收获协同卸粮试验，验证控制方法的性能和适应性。

1 双机纵向相对位置协同原理

自主收获精准协同卸粮的作业状态如图1所示，其中收获机和运粮车平行行驶。为了精准卸粮，需要同时控制收获机Ph坐标(xh，yh)和运粮车Pt坐标(xt，yt)，使卸粮筒出口Pu与卸粮目标点Pb重合。Pu与Pb的相对横向距离dp通过调节两车的直线跟踪路径距离来控制。相对纵向距离dp通过调节运粮车的车速来控制。

分析协同作业时双机的几何关系（图1b），设置基准线为过运粮车定位点的运粮车行驶方向直线，dp为目标卸粮点Pb与卸粮口Pu在基准线上的投影距离，几何模型如式（1）所示：

使用上述模型时由于收获机、运粮车和拖斗的航向存在高频摆动，全部引入模型，容易引起控制振荡，根据前期试验，双机在直线导航跟踪过程，车辆和拖车航向摆动的标准差小于0.06°，且变化分布类似白噪声，所以将α和β设为0。据此可以将上述模型简化为平行协同模型，如图1c所示。假定双机在跟踪平行路径时，航向稳定且与目标直线相同，拖斗也与拖拉机位于同一直线上。这一假设能够降低模型复杂度，同时提高控制目标的稳定性，排除航向波动引起的高频干扰。由于简化模型中拖车、拖斗和收获机航向相同，所以可以对进行Pb平移，向前平移la的距离，使得le=lb+lc-la，le为Pb到Pt的距离，通过Ph的投影计算dp，计算方程为

2 纵向相对距离协同控制框架

收获机与运粮车分别规划行驶路径，双机协同目标路径平行，通过设定目标路径间距来调整两车横向相对距离，由于所采用的直线跟踪方法精度为2.5 cm[19]，所以双机协同横向相对距离控制精度能达到5 cm。本文主要研究纵向相对位置偏差控制方法，通过改变运粮车油门大小进行调节。

纵向相对位置控制框架如图2所示，收获机为主机，运粮拖拉机为从机。对主机和从机的位置和速度进行差分，获得主从机的相对位置和速度，输入至位速耦合控制器得到期望发动机转速。将期望值通过CAN总线输入到发动机电子控制器（Electronic Control Unit，ECU），从而改变从机前进速度，实现纵向相对位置控制。

3 位速耦合控制器设计

控制两车的相对位置需要对位置和速度进行耦合控制，依据当前的位置和速度差改变油门控制的策略。

本文将位速控制分为2个分量，一个为速度一致性决策分量，另一个为位速综合决策分量，速度一致性决策分量upd与位速综合决策分量ubang-bang加权求和得到位速耦合控制器输出uo，uo为发动机转速变化率，控制器结构简图如图3所示。

式中bbang-bang为求和权重，通过仿真优化整定。

由于两车在协同行驶过程中，油门与速度系统具有较高的延时和非线性特点，所以在控制的过程中设置死区以提高稳定性，纵向偏差处于死区范围内时速度需要保持相对稳定。如果仅使用相对位置PD控制，易出现超调和振荡现象。速度偏差是位置偏差的微分，引入速度一致性决策分量，可提高控制系统阻尼，消减振荡。

速度一致性决策分量为PD控制。主要作用是协调两车速度，在位速综合决策分量死区范围内仅依靠该决策分量进行控制：

位速综合决策分量通过基于动力学原理的Bang-Bang控制模型计算，假设拖拉机在仅控制油门的情况下，最大合力为Fmax，最大加速度为amax，当前纵向速度偏差为ev时，依据能量守恒方程Fmaxd=1/2mev2，以最大加速度amax改变车速使得ev减小为0时，运粮车与收获机的相对行驶距离d为

式（4）～（5）中m为车体质量，kg；kp为比例增益系数，t为时间，s。

依据上式知当纵向相对位置偏差ed和速度偏差ev的数学关系为式(5)时，执行加速度为amax的减速，即可使纵向偏差ed和速度偏差ev同时收敛至0。据此可以设计控制滑模开关函数f(ev)，通过该函数判断两车的当前状态，并改变控制策略，具体设计如下：

车辆通过油门大小实现加速或减速功能，不涉及换挡或者刹车，加减油门的最大变化率基本相同，所以最大加速度amax和减速度-amax的数值相近。依据述能量守恒原理，结合公式(5)设计滑模开关函数ed=k1ev2、ed=k2ev2、ed=-k1ev2和ed=-k2ev2，其中k1和k2为接近的值，针对滑模面控制抖振问题，设置这2组滑模开关函数构建死区消除抖振。位置阈值ed=(-0.25， 0.25)是距离精度死区，ed=(-0.8，-0.25]和ed=[0.25，0.8)是分段控制范围，大于该距离分为一段，速度阈值ev=(-0.06，0.06)是速度精度死区，ev=(-0.1，-0.06]和ev=[0.06，0.1)是分段控制范围，大于该速度范围分为一段，综合上述阈值设计位速综合决策方法，如图4所示。

位速综合决策方法依据两车相对位置偏差ed和相对速度偏差ev值将状态分组如下：

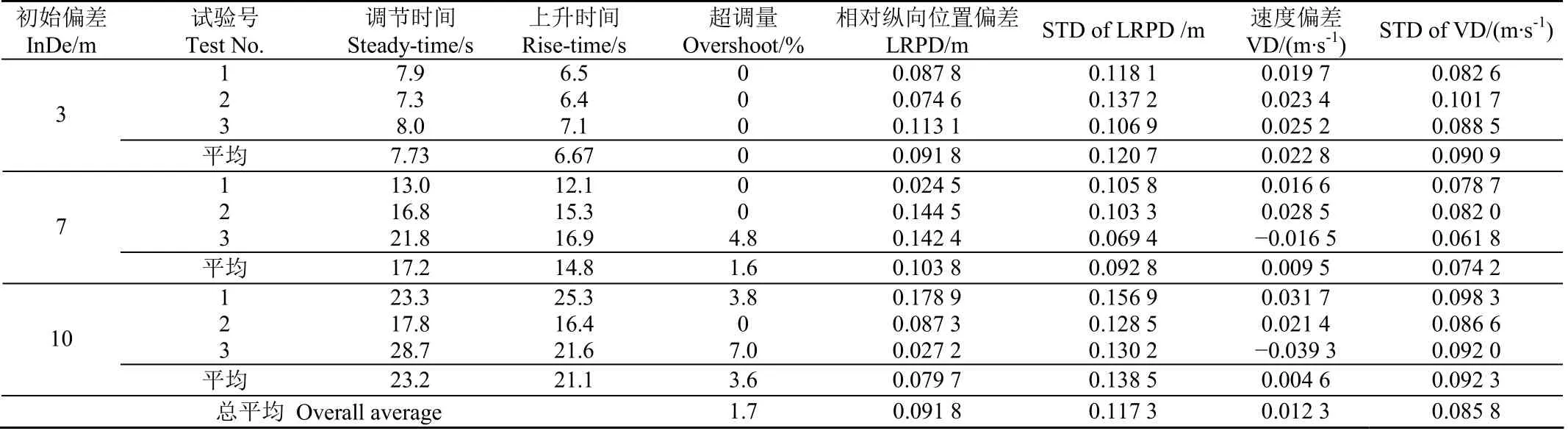
A：{-0.25

B：{-0.25

C：B关于y轴的对称区域，输出分量为-a1；

D：{-0.25

E：D关于y轴的对称区域，输出分量为-a2；

F：{0.25≤ed<0.8,ed>k1ev2}的非闭合区域，输出分量为a3；

H：F关于原点的对称区域，输出分量为-a3；

I：{-0.8-k2ev2}的非闭合区域，输出分量为a4；

J：I关于原点的对称区域，输出分量为-a4；

K：{ed≤-0.8,ed>-k2ev2}的非闭合区域，输出分量为a5；

L：K关于原点的对称区域，输出分量为-a5；

M：{ed≥0.8,ed>k1ev2}的非闭合区域，输出分量为a6；

N：M关于原点的对称区域，输出分量为-a6。

4 纵向相对位置控制系统仿真模型

建立纵向相对位置控制系统仿真模型，用于控制器设计、控制参数优化和控制性能研究。

4.1 行驶速度系统模型辨识

建立纵向相对位置控制系统仿真模型需要获得运粮车油门与行驶速度的传递函数模型。但通过发动机转动模型、变速箱传动模型和轮胎摩擦驱动模型正向推导运粮车油门与行驶速度的传递函数模型难度较大，模型中部分参数未知，无法拆分各部分进行参数整定。所以本文采用阶跃响应面积辨识法获取系统传递函数[16]。

进行了阶跃响应试验，将期望转速从1 000阶跃为1 400，通过BDS(BeiDou system)系统测量获得拖拉机速度上升了0.3 m/s，记录速度变化曲线，采样率为10 Hz，对数据进行归一化处理，再通过面积辨识方法，计算获得二阶传递函数如式（6）所示。试验数据与辨识模型阶跃响应G(s)如图5所示，该辨识模型的R2为0.988 1，满足建立仿真模型的要求。

式中s为复参数。

4.2 纵向相对位置协同系统仿真模型

仿真模型输入包括主机的前进速度、初始纵向相对位置和初始从机行驶速度。将纵向相对位置偏差和相对速度输入位速耦合控制器，计算出发动机转速变化率，由转速变化率积分获得当前发动机转速。通过基于面积辨识所获得的传递函数计算出从机车速，该车速与主机车速差为相对速度。相对速度的积分与初始纵向相对位置的和为当前相对位置。依据拖拉机发动机转速可调节的最大和最小速度，对仿真速度进行限幅，速度限幅范围为0.3～2.0 m/s；针对发动机转速变化率进行限幅，变化率限幅范围为-300～600 r/s。纵向相对位置控制Simulink仿真模型如图6所示。

4.3 仿真模型验证

为验证仿真模型是否符合实际情况，在雷沃阿波斯智慧农业示范基地的试验田进行仿真模型验证试验：

1）设计收获机与运粮车协同试验，根据收获机常规收获速度，设置主机速度为1 m/s。根据所设计位速耦合控制算法，可知纵向相对位置偏差大于8 m时，控制器计算输出已经大于最大油门变化值，而被限幅，运粮车将开最大油门前进，再设置更大初始偏差，收敛过程相似。所以设置初始相对偏差为8 m具有一定的代表性；

2）通过BDS-GNSS双天线系统采集车辆速度，RTK-GNSS定位模块（司南公司的K728），定位信息获取频率为10 Hz，水平定位精度±(10+D×10-6)mm，D为基站到移动站的距离，km；

3）设置相同的初始条件，将所得结果与仿真模型的结果进行对比，结果如图7所示（图中的实际数据的毛刺来源于其他数据对通讯信道占用导致的处理延时）。仿真系统与实际系统的调节时间相差2.1 s，上升时间相差1.3 s，稳态偏差相差0.19 m，所构建仿真系统满足仿真分析要求。

4.4 位速耦合控制器参数仿真优化

位速耦合控制器中的关键参数包括2个分控制器的系数kp、kd、bbang-bang、a1、a2等。根据前期试验[30]可知将拖拉机发动机转速变化率控制在300 r/s以内控制过程中没有明显的顿挫现象。以上述变化率改变油门大小，最大转速变化率为5.0 r/s，预设a1至a6参数分别为1.5、2.5、3.0、0.5、2.5和5.0 r/s。基于初步测试结果，参数的优化组kp设置为0.025～0.75之间的30等分组，kd设置为1.5～4.0的6等分组，bbang-bang设置为0.1～1.0的10个等分组。主机速度设置为1 m/s，相距距离为8 m，用这30×10×6组参数进行全因子试验获得纵向控制响应数据。性能指标综合时间绝对误差（Integral Time Absolute Error，ITAE）[31]重点关注动态性能，加入随机噪声后的稳态性能对该指标的影响较低。本文希望能兼顾纵向相对位置协同控制的动态性能和稳态性能，根据文献[32]，系统时域响应的性能指标包括上升时间tr、调节时间ts、稳态偏差e、标准差σ和超调量Mp。设计本文的参数优化性能指标J如式（7），综合考虑阶跃响应性能指标的物理实际意义，各项指标的优化方向都是降低数值，加权求和能够代表动态和稳态性能。

由于各项阶跃响应性能指标的数值范围存在差距，直接求和会使数值较大的指标削减数值较小指标的影响，所以本文将正常收敛过程中的几个指标数值调整到基本相同的范围内，使所设计的指标能够兼顾动态性能和稳态性能，仿真试验中稳态偏差、标准差控制目标在0.2 m左右，所以稳态指标权重bj2设为15，超调量单位为%，控制目标在4%即0.3 m以内，所以超调量指标权重bj3设为100%，仿真时间设为35 s，分析得出的上升时间与调整时间在0～35 s，所以时间权重bj1设为1/35。采用该性能指标筛选出适合纵向相对位置协同控制的参数，分析参数适应性，剔除极端参数。

通过全因子试验获得参数响应曲面，对响应数据进行对数处理，将指标调整到适当的大小，同时保留指标的相对关系：

为了提高优化结果的泛化能力和鲁棒性，使用二维卷积核式（9）对响应曲面进行特征提取，获得处理后的参数性能响应曲面如图8所示。

由图8可知，最优性能指标出现在kd=3.0时，此时kp、kd和bbang-bang分别为0.2、3和0.8。

依据上述优化方法对速度0.5、1.0和1.5 m/s进行参数寻优，结果如表1所示。由于该方法基于动力学原理设计，参数响应曲面平缓，最优参数速度适应性较好。

表1 位速耦合控制参数优化结果 Table 1 Position-velocity coupling control parameter optimization results

由于实际协同过程中可能存在干扰导致控制超调，运粮车超车至收获机前方，相对位置偏差为负。为验证最优参数在初始偏差为负值时的控制效果设计验证试验，仿真模型同上文，初始偏差为-8 m，3组试验主机速度分别设为0.5、1.0和1.5 m/s。响应曲线如图9所示。平均稳态偏差绝对值分别为0.027 5、-0.068 9和0.056 0 m；稳态标准差分别为0.034 9、0.026 9和0.026 3 m；上升时间分别为14.7，12.7和12.7 s；调节时间分别为16.7，14.9和14.9 s。试验结果表明所设计方法负向初始偏差响应收敛。

为验证性能指标权重的变化对优化后最优参数控制率的影响，设计了一组对比试验，改变性能指标的权重比例，寻优后采用结果参数，并分析寻优参数的响应数据，步骤如下：

1）设置速度为1.5 m/s，初始偏差为8 m，试验组1中权重bj2设为15，试验组2中权重bj2设为25，提高其中一个权重，其他权重则相对降低；

2）采用上述优化方法获得2组最优参数kp、kd、bbang-bang分别为0.2、3、0.8和0.1、3、0.7；

3）采用上述2组参数进行仿真试验，初始偏差为8 m，主机速度设为1.5 m/s。

试验结果如图10所示，第1组相较第2组上升时间减少0.07 s，调节时间减少0.02 s，稳态偏差增加0.007 9 m。理论上改变指标的权重能够改变最优参数控制率的响应指标，可以根据需求整定最优参数。但是试验结果表明，由于最优参数附近的响应曲面平缓，这些参数的响应数据各项性能指标都很相近，实际作用不显著。

4.5 控制性能对比仿真试验

为了研究位速耦合纵向相对位置控制方法与传统PD方法[25]的差异，设计了双PD纵向相对位置控制器，将速度误差PD反馈和位置偏差PD反馈相加获得控制输出。

针对位置偏差PD控制器的参数运用上文相同的优化方法进行参数优化，结果如表2。参数优化结果表明，位置偏差PD控制方法与主机速度的相关性比位速耦合控制方法高。

表2 位置偏差PD控制参数kp_d和kd_d的优化结果 Table 2 Position deviation PD control parameters kp_d and kd_d optimization results

仿真对比试验设计：3组对比试验，主机速度设置为0.5、1.0和1.5 m/s，位速耦合控制器参数kp、kd和bbang-bang分别设置为0.2、3和0.8，双PD控制器参数kp、kd、kp_d和kd_d分别设置为0.2、3、0.5和3.75，测试控制方法的速度适应性，性能指标包括上升时间、调节时间和超调量。试验验结果如表3所示。试验结果表明：

表3 控制性能仿真对比试验 Table 3 Simulation and contrast test of control performance

1）主机速度为0.5 m/s时，最优参数下本文方法相较双PD方法，上升时间减小3.8 s，调节时间减小10.2 s；

2）主机速度为1.0 m/s时，最优参数下本文方法相较双PD方法，上升时间增加4.7 s，调节时间增加5.7 s；

3）主机速度为1.5 m/s时，本文方法依然稳定，而双PD方法出现135%的超调，且收敛较慢。最优参数下本文方法相较双PD方法，上升时间增加1.0 s，调节时间减小42.7 s，超调量减小135个百分点。

上述分析表明，采用传统PD方法能够获得良好性能，但是参数速度适应性较差。由于实际作业时针对不同农机、地况和不同主机速度，难以进行人工全局整定。

5 双机协同纵向相对位置控制方法性能试验

5.1 试验系统

为了研究位速耦合纵向相对位置控制方法的适应性和精度，搭建了双机导航协同收获试验系统，系统由收获机和运粮车组成，收获机（雷沃重工GE80S-H）与运粮车（雷沃重工M1104）均具备电控底盘，能够实现电控转向与发动机转速控制，主要参数如表4。采用RTK-GNSS定位模块（司南公司K728），定位信息获取频率为10 Hz，水平定位精度±（10+D×10-6）mm；车轮转角传感器采用BEI-9902120CW，非线性度为±2%，A/D采样精度为12位；转向执行机构为力士乐公司的HT801053；双机通讯采用2组2.4 GHz频率通信模块（EBYTE公司的E34-DTU(2G4D20)），模块与控制终端通过RS-232通讯；控制终端为AGCS-Ⅰ控制器和触控显示屏，控制终端通过CAN总线与双机的底盘电控单元（Electronic Control Unit）通讯；位速耦合纵向相对位置控制方法移植于AGCS-Ⅰ控制器内。软件部分采用Metrowerks Code Warrior for ARM Developer Suite v1.2开发。系统结构和试验平台如图11与图12所示。

5.2 试验方案

协同系统试验在雷沃阿波斯智慧农业示范基地进行，对主从系统分别规划目标直线路径，采用预瞄点导航控制方法[17]控制横向偏差，采用本文所设计的位速耦合纵向相对位置控制方法进行纵向偏差控制，控制器参数kp、kd和bbang-bang分别设置为0.2、3和0.8。收获机（主机）行驶速度按照实际作业需求设置为1 m/s，运粮车（从机）进行跟随，运粮车手动档位设置于中一档，通过调节发动机转速进行位速协同，可调范围在0.7～1.6 m/s之间。设置3个水平的初始纵向相对位置偏差进行控制性能试验，分别为3、7和10 m，代表短距、中距和长距的跟踪过程，每组初始距离进行3次重复试验。以10 Hz频率对纵向相对位置偏差和纵向相对速度偏差进行记录。

以平均稳态纵向相对位置偏差和稳态纵向相对位置偏差的标准差σd为双机进入稳定协同状态时的相对纵向距离控制精度指标，以平均稳态纵向相对速度偏差和稳态纵向相对速度误差的标准差σv为双机进入稳定协同状态时的纵向相对速度控制精度指标；以双机协同纵向相对位置控制稳态时间ts、上升时间tr和超调量Mp反映控制方法在跟踪过程中的收敛性能。通过以上指标分析控制质量。

5.3 结果与分析

设置3、7和10 m初始纵向相对位置偏差的3组重复试验结果如表5所示。通过不同的试验结果可知本文提出的控制方法和优化参数的适应性较好，试验结果可重复性良好。全部试验的平均稳态纵向相对位置偏差绝对值为0.091 8 m，稳态纵向相对位置偏差的标准差为0.117 3 m，控制精度满足协同卸粮作业需求，对其他作业如加种加油同样可行。平均超调量为1.7%，平均稳态速度偏差为0.012 3 m/s，协同过程平稳，在可调速度范围内实现了纵向协同控制。

表5 不同初始偏差下纵向相对位置控制试验结果 Table 5 Longitudinal relative position control test results with different initial deviations

文献[25]中田间协同试验中主机速度为0.83 m/s时，试验结果表明两机的相对位置平均偏差为0.13 m，方差为0.15 m。文献[23]在仿真系统中运用滑模变控制方法控制2台农机的纵向相对位置，仿真试验结果表明平均偏差为0.106 m。与上述研究比较，本文针对运粮车行驶系统建立简化平行协同模型和运动学模型，进行了系统模型辨识和控制参数优化，并通过田间验证了所设计方法的相对位置平均偏差分别降低29.2%和13.2%。

6 田间作业试验

为验证位速耦合纵向相对位置控制方法在实际收获作业时的控制质量，2019年7月在甘肃金昌进行了双机协同小麦收获试验。试验场景如图13所示。

依据待收获小麦田块规划U型收获路径。收获路径沿待收区域设定，收获机路径向前进方向左侧平移4.5 m设置为运粮车行驶路径，形成一个大U型路径嵌套于收获的U型路径外侧。保证粮筒展开后卸粮点位于运粮车中轴线附近。依据小麦收获常规作业速度，速度设定为1 m/s，运粮车跟随接粮。只在直线收获路径上卸粮，接近转弯时停止卸粮并收回卸粮筒。协同模式中运粮车与收获机从田头并排起始。收获机为主机，运粮车为从机。收获机先作业，运粮车等待收获机的启动信号再启动。运粮车行驶在外圈，行程大于收获机，为了安全作业转弯时需要前后错开，所以田间试验运粮车初始纵向位置偏差为正。初始偏差非人为设置，由协同作业自然形成。试验指标与前文一致。

小麦收获试验的双机协同轨迹如图14a所示，协同过程分为来去2段，分别编号为1和2。纵向相对位置偏差和纵向速度偏差如图14b、图14c所示，各项性能指标如表6所示。平均稳态纵向相对位置偏差绝对值为0.077 8 m，稳态纵向相对位置偏差的标准差为0.091 3 m。协同精度能够满足收获协同卸粮的需要。

表6 双机协同收获纵向相对位置控制试验结果 Table 6 Two-machine coordinated harvesting longitudinal relative position control test result

7 结 论

针对自主导航收获协同卸粮过程中纵向相对位置控制需求以及拖车驱动系统非线性度较高的问题，本文构建了简化平行协同模型，设计了位速耦合纵向相对位置控制方法，结合直线跟踪控制方法，实现了双机收获协同卸粮作业，主要结论如下：

1）为研究所设计方法的实际性能，进行了不同初始纵向偏差的田间双机协同试验。主机速度为1 m/s，初始纵向偏差分别为3、7和10 m时，平均调节时间分别为7.73、17.2和23.2 s。田间试验平均稳态偏差绝对值为0.091 8 m，速度平均稳态误差为0.012 3 m/s。由于运粮车系统目前还无法自动切换高低档位，通过发动机调节前进速度范围有限，所以未进行不同速度主机的适应性研究，研发自动切换高低档位的运粮车系统，能够进一步深入研究控制方法的速度适应性。

2）为优化控制器参数建立仿真模型。采用面积辨识法获取了油门车速开环二阶传递函数，并基于该传递函数设计拖拉机速度控制仿真模型。运用该模型获取了控制器优化参数，进行本文方法与传统PD方法的对比试验，试验结果表明，主机速度为1.5 m/s时，本文方法相较传统PD方法，上升时间减小1.0 s，调节时间减小42.7 s，超调量减小135%。本文方法克服了传统PD方法参数速度适应性差的问题。

3）实际协同收获作业表明，主机速度在1 m/s时，纵向相对位置控制收敛，平均稳态纵向相对位置偏差为0.077 8 m，稳态纵向相对位置偏差的标准差为0.091 3。能够适应实际作业工况，协同精度能够满足收获协同卸粮的需要。