无沟铺管机北斗导航控制系统设计与试验

王吉中，赵 博，赵士猛，邢高勇，伟利国，胡小安

（中国农业机械化科学研究院，北京 100083）

0 引言

农田暗管排水系统利用人为埋入地下的孔管排出土壤中多余水分与盐渍[1-2]，具有防涝、控盐、节水节地、改善生态条件等多重功能[3]。其中，暗管铺设直线性[4]关乎系统的工作性能、工程寿命和可维护性，乃至系统运行的经济效益[5]。传统方法通过人工瞄准标桩控制铺管直线性[6-7]，不仅抬高了经验和技术门槛、耗费工人精力，而且精度很难保证。近年来，通过铺管机自动控制系统调节左右轮速实现直线性控制，但仅适用于土壤质地均匀、附着条件良好的平整地表[7]。因此，亟需开发自动化程度高、环境适应性好且符合铺管直线性要求的铺管机导航系统，以满足实际工程需要。

目前，激光导航、视觉导航和卫星定位导航等技术已应用至农机领域[8-10]。其中，卫星定位导航使用便利、性能稳定且无需参照物，尤其适合农田暗管排水系统大面积施工场景。近年来，Han等[11]基于GNSS、RTK和运动传感器开发出一套低成本的履带车辆自动驾驶系统，并提出一种多传感器数据融合算法。试验表明，路径跟随均方根误差小于9 cm，最大误差小于30 cm。Takai等[12]基于RTK-GPS和惯性传感器，采用自适应控制算法，实现履带拖拉机自主导航。试验表明，横向误差的均方根小于5 cm。伟利国等[13-14]通过融合GPS定位信息、姿态信息和行走速度检测运行轨迹，采用模糊控制方法实现开沟铺管机导航，试验表明，直线跟踪误差不超过10 cm。宋彦等[15]提出一种基于启发式动态规划算法的路径跟随控制方法，并设计出一种适用于履带式机器人的路径跟随控制系统。试验表明，算法的直线跟踪平均误差绝对值为4 cm、均方根误差为6 cm。丁幼春等[16]基于免疫比例-积分-微分（Proportion-Integral-Differential, PID）控制算法设计出一种适用于履带车辆的导航控制器，田间试验表明，作业速度为0.5 m/s时，直线跟踪平均绝对偏差为5.8 cm，最大偏差为15.2 cm。上述研究表明，履带式农机自动导航系统较少，且现有研究多以小型装备为主，缺乏针对大型履带农机装备自动导航技术的研究。

本研究基于载波相位差分技术的北斗定位系统（Real Time Kinematic-BeiDou Navigation Satellite System, RTK-BDS）实时获取铺管机定位和航向信息， 采用后向反馈（Back Propagation, BP）神经网络预测当前行驶状态，然后选择器依据预测结果确定控制参数，并通过自适应PID控制算法实现履带式无沟铺管机导航控制，以满足铺管直线性需求。

1 无沟铺管机系统构成及原理

1.1 整机结构与原理

本研究基于中国农业机械化科学研究院研制的PV1509HT型V形犁式无沟铺管机（如图1）。作业时，使用V形犁体切开土壤，并掀起一个三角形土垡，柔性波纹管道经犁体内的导管进送至土垡底部，从而完成管道铺设。为了保证V形犁正常作业，需要机器提供较大的牵引力。但由于田间土壤存在松软差异和高低不平，势必导致车辆行驶偏摆，进而影响管道铺设的直线性。因此，迫切需要为机器设计导航控制系统，以保证铺管作业质量。

1.2 导航控制系统

该机采用双泵双回路全液压驱动的履带行驶系统，其导航控制原理如图2所示。机载控制器读取RTK-BDS和各传感器的工况信息，并依据暗管施工设置，通过脉冲宽度调制（Pulse Width Modulation, PWM）波控制比例阀调节左、右行走泵排量大小，进而改变左、右行走马达转速，实现导航控制。

2 无沟铺管机数学模型

2.1 履带转向运动学模型

在水平地面上，铺管机稳定转向行驶[17-19]如图3所示，点O为整机的转向瞬心，从O点到履带纵向对称平面的距离R为转向半径。机器任意一点至点O的距离乘以角速度ω，即为该点的绝对速度，因此两履带的绝对速度分别为

式中B为履带轨距，m；V1为外侧履带绝对速度，m/s；V2为内侧履带绝对速度，m/s。

根据两侧履带的绝对速度可求得转向半径R为

单位时间内的偏航角度θ为

实际情况中，履带会发生滑转。引入滑转速度后，求得内、外侧履带的绝对速度为

式中1V'、2V'为考虑滑转的外、内侧履带绝对速度，m/s；ΔV1、ΔV2为外、内侧履带滑转速度，m/s。

此时，可求得实际转向半径R′不再等于R。

所以，受履带滑转的影响，回转中心实际与点O并不重合。因此，针对不同的滑转情况，应采取不同的控制方式。

2.2 导航偏差模型

在控制铺管机导航行驶时，首先判断机器与预设铺管参考线的相对位置，再采取不同的策略控制车辆行驶，图4显示了相对位置的9种情况。

预设用于确定参考线的两点M和N坐标分别为和，其中或。如图5所示，可求得参考线方程为

由RTK-BDS可获得铺管机当前位置为K(x0,y0)，则铺管机与参考线的横向误差d为

其中

假设以正北方向为起始方向，沿逆时针旋转为正，由图6可求得铺管参考线方向角α(0°≤α＜360°)为

其中

由磁力计可实时获取铺管机的航向角β，则航向误差Δθ为

3 基于BP神经网络的导航控制系统

导航控制流程如图7，预先通过试验获取模态分类和相应控制参数，并存储在知识库内，同时采用试验数据训练BP神经网络。导航控制时，首先采用霍尔传感器检测左、右行走马达速度vL、vR，采用RTK-BDS获取铺管机绝对速度v，通过控制器局域网络（Controller Area Network，CAN）通信读取发动机功率P，采用压力传感器检测左、右行走泵的压力pL、pR，然后将上述参数值输入至BP神经网络，并预测铺管机当前时刻的模态分类。根据神经网络的预测结果，选择器从知识库中选择自适应函数F(x)和H(x)，以及PID控制参数，分别发送给自适应比较器和控制器。自适应比较器依据横向误差和航向误差，通过自适应函数选择横向或航向控制器，实现导航控制。

3.1 BP神经网络设计

将铺管机的可控性分为4种模态，每一模态对应知识库中不同控制参数。通过BP神经网络预测模态，以适应复杂田间环境下的各种工况。BP神经网络架构如图8所示。

BP神经网络由输入层、隐含层和输出层构成[20]。其中，输入层设计有6个神经元，分别对应左行走马达速度vL、右行走马达速度vR、车辆实际平均车速v、发动机功率P和左、右侧行走泵压力pL、pR的输入。由于各输入变量的单位不一致且数值范围相差较大，提前依据最大最小原则[21]进行归一化，即

式中 ,ijξ为输入变量i的第j个值；ξ,mini为输入变量i的最小值；ξ,maxi为输入变量i的最大值。

输出层包含4个神经元，分别对应4个控制模态。输出层中某神经元输出为1时，代表铺管机的可控性处于该模态，输出为0时代表可控性不处于该模态。

隐含层神经元个数可由式（15）[22]确定为8个。

式中n为隐含层神经元个数；n1为输入层神经元个数；n2为神经元个数；a为可变系数。

输入层和隐含层中，每个神经元的激活函数均采用tanh函数

由于输出层的输出值只有0和1两种，则输出层的激活函数采用sigmoid函数

获得该神经网络的输出值后，使用概率最大阈值函数判断系统状态

式中max为阈值分割系数，取输出层4个神经元输出值中的最大值。

1.制度完善。联合体是由多个独立经营的新型农业经营主体，通过完备的制度体系组成的农业产业化经营组织联盟。制度体系包括四个层次：一是由联合体成员共同制定的章程，含经营宗旨、业务范围、成员义务和权利、代表大会等组织机构及其职责、决策机制、退出机制、资产管理等内容；二是主导产业的建设方案，含基本情况、经营目的、运营内容、保障措施、办公场所等；三是规范各成员生产经营行为的标准体系，含家庭农场（或专业大户）和生产类合作社的技术规程、服务类合作社的行为准则、仓储管理制度、财务管理制度、可追溯管理制度等；四是主体之间签署的生产、服务等契约合同。

3.2 自适应比较器设计

作业时，铺管机的犁体深入土壤，因此在导航控制时，机器转向角度不能过大，不然轻则影响犁体切割土垡，重则导致暗管折断。为保证在不影响犁体正常工作的同时，能够快速减小导航误差，设计了自适应比较器。

在获取到航向偏差和横向偏差后，自适应比较器使用自适应函数F(x)和H(x)，分别计算两个偏差的比较值。当航向偏差的比较值更大时，比较器命令控制器进行横向控制，否则进行航向控制。经过如此反复调整，可保证铺管机的航向偏差和横向偏差均逐渐减小，而不会出现瞬时转向角度过大的现象。

3.3 模态选择器设计

为了应对神经网络的预测结果中可能出现的模态重叠现象，即同时存在两个或两个以上模态，设计了模态选择器。

模态选择器包含知识库和选择器。知识库中存储着预先通过试验得到的4种控制模态参数，每一种模态参数包含有比较器的自适应函数和PID控制参数。

选择器依据神经网络预测的控制模态做出判断，再从知识库中调用相关模态的参数，并发送给控制器和比较器。选择器的选择规则为：若仅有1个模态预测结果，则选择该模态为当前模态；若有2个连续的预测结果，则选择控制难度更高的模态为当前模态；若有2种不连续的预测结果，则与上一时刻模态组合，选择3个模态的中间模态作为当前时刻的模态；如果有3个及以上预测结果，则保持前一时刻的模态。

4 田间试验

2020年12月，在山东省德州市庆云县开展田间试验，采用5点取样法测试土壤的含水率平均值为24.2%，坚实度平均值为527.2 kPa。田间试验现场如图9所示。

4.1 铺管机模态控制试验

4.1.1 确定模态控制参数

为获取不同负载下的铺管机控制模态，在平整度偏差为±2 cm的地面上，铺管深度从0开始，每次增加0.05 m。每组试验中，铺管机以0.2 m/s的速度行驶10 m。

自试验开始起，一直采用满足作业要求的同一套参数实现导航控制，直到第24组试验（铺管深度1.2 m）时，横向误差大于0.04 m，此时记0～1.2 m过程中的控制参数为第一模态控制参数。保持1.2 m铺管深度，再次调整控制参数，直至满足作业要求，一直沿用至第30组试验（铺管深度1.5 m）时，横向误差再次大于0.04 m，此时记1.2～1.5 m过程中的控制参数为第二模态控制参数。按上述步骤继续试验，直到第36次，铺管深度为1.8 m时，铺管机原地滑转，地面行驶速度微乎其微，试验终止。最后得到1.5～1.65 m过程中的控制参数为第三模态控制参数；1.65～1.8 m过程中的控制参数为第四模态控制参数。

4.1.2 模态控制试验

使用4种模态控制参数对所有模态分别进行导航控制试验，横向误差结果如表1所示。

表1 模态控制横向误差 Table 1 Lateral error of modal control cm

由表1可知，每种模态控制参数在各自模态下的横向误差均在±4 cm范围内，即每种模态控制参数都能够适应各自状态的控制。但是，在其他的作业深度分组时，误差超过±5 cm范围，甚至不可控。

4.2 BP神经网络样本采集

在确定控制模态参数的试验中，通过传感器采集，得到每个控制模态下铺管机的状态参数。在36组试验数据中，各随机选取100条试验数据，作为BP神经网络的训练集。

4.3 上线控制试验

铺管作业前，机器应到达预定的参考线上，即首先进行上线操作。上线过程中，犁体完全离开地面，即铺管深度为0，符合第一控制模态的工况，因此直接使用相应的控制参数实现导航，试验结果见图10。

由图10可知，在一定的初始偏差下，铺管机逐渐靠近参考线，上线初期出现了一次超调，但之后与参考线的距离逐渐减小。上线期间的航向误差如图11所示，横向距离误差如图12所示。

由图11可知，在上线初期会不时地纠正铺管机航向，最大航向误差在±9°范围内。上线后，航向误差在±4°范围内。由图12可知，在控制初期，横向误差不断减小且减小的速度不断放缓，在出现4.58 cm的超调后，铺管机与参考线间横向误差的波动逐渐减小，最终稳定在±2.6 cm之内。

4.4 直线导航试验

在1.6 m的恒定铺管深度下，以0.2 m/s的铺管速度，沿预设铺管参考线作业，以验证导航控制的效果，航向误差和横向误差如图13和图14所示。

图13 和图14表明，航向误差在±5.5°之内，横向误差在±3 cm之内。航向和横向误差较大的情况虽偶有出现，但在96.2%的情况下，航向误差在±3°之内；在89.6%的情况下，横向导航误差在±1 cm之内。因此，该导航控制能够满足铺管机直线性作业要求。

4.5 工程应用试验

试验区域地面平整度偏差为±10 cm，选取施工作业中最为常见的几种铺管深度，设置坡降比例为3/10 000 （每100 m深度减小3 cm），进行导航直线性控制试验，结果如表2所示。

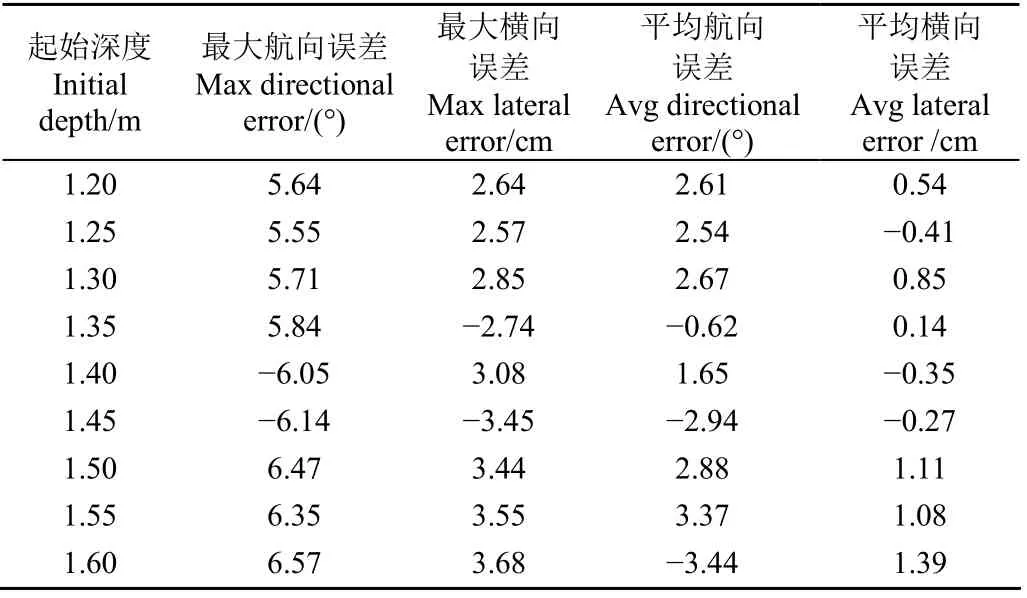
表2 无沟铺管机在不同铺管深度工况下试验结果 Table 2 Test results of the pipelayer under different initial depths

由表2可知，航向误差控制在±7°范围内，平均航向误差在±3.5°范围内，最大横向误差在±4 cm范围内，平均横向误差在±1.5 cm范围内，满足铺管机作业要求。

5 结 论

1）基于载波相位差分技术的北斗定位系统（Real Time Kinematic-BeiDou Navigation Satellite System, RTK-BDS）设计了多模态自适应比例-积分-微分（Proportion-Integral-Differential, PID）控制算法。算法使用后向反馈（Back Propagation, BP）神经网络判断无沟铺管机的控制模态，采用自适应PID控制算法控制铺管机导航，用于改善无沟铺管机的适应性。

2）通过试验获取铺管机模态分类及BP神经网络训练样本数据后，开展一系列导航控制试验。上线试验中，横向距离超调为4.58 cm。直线导航试验中（铺管深度1.6 m），航向误差在±5.5°范围内，最大横向误差在±3 cm范围内。工程应用试验中（坡降比例3/10 000），航向误差控制在±7°范围内，最大横向误差在±4 cm范围内。上述结果表明，该导航控制系统能够满足V形犁式无沟铺管机的作业要求。