考虑整体趋势的最佳子集Kriging模型

谭佳斌，赵维涛

(沈阳航空航天大学 航空宇航学院, 沈阳 110136)

1 引言

面对大多数复杂的工程结构设计问题，为获取设计参数与结构响应之间的关系，工程技术人员往往采用代理模型。实践表明，代理模型具有精度高、计算量小，低误差等特点[1]，可广泛应用于航空航天等领域。现有较为常用代理模型主要有：响应面法[2]、神经网络法[3]、支持向量机[4]和Kriging模型[5-7]等。由于Kriging模型具有良好处理非线性预测能力，Kriging模型已成为最具代表的代理模型之一。

为完善Kriging模型，研究者已经进行了大量的研究工作。增强梯度Kriging模型[8]，优点在于通过利用梯度信息来提高Kriging模型的计算精度。Kennedy等人将协同Kriging模型[9]推广到工程领域，该模型通过用容易抽样的量替换较困难抽样的量来进行辅助预测。Joseph等人提出了盲Kriging模型[10-12]，通过贝叶斯法识别趋势函数。Kwon等人提出了趋势Kriging模型[13]，但趋势函数求解过程不利于工程实际问题的求解。

本文提出了一种改进的Kriging模型。与以往的Kriging模型不同的是：

1) 在生成初始样本后，本文通过响应面法确定趋势函数。考虑到实际工程问题，本文使用一至三阶不含交叉项的多项式函数作为备选趋势函数，通过回归分析计算出趋势函数的相关系数，选取趋势拟合程度较高的备选趋势函数的阶数作为Kriging模型整体趋势函数的阶数。

2) 在确定趋势项的阶数后，将整体趋势函数中所忽略的交叉项重新加入Kriging模型中，通过遗传算法重新筛选基函数，排除对模型计算精度无影响或者影响极小的基函数项，保留影响较大基函数项，降低计算量的同时提高模型的精度。

2 本文方法

经典Kriging模型包含整体趋势函数和随机函数2个部分。已有研究表明，在样本数量足够多的情况下，整体趋势函数对Kriging模型的预测精度影响较小[9-13]。然而足够多的样本必然带来计算成本的增加，不利于工程实际。因此，在样本数量有限的情况下，正确选取整体趋势函数有助于提高Kriging模型的预测精度。本文首先利用响应面方法确定Kriging模型整体趋势函数的阶次，然后通过遗传算法对整体趋势函数中的各项进行优化选取。

2.1 初始样本点

利用拉丁超立方抽样方式生成初始样本，并求得对应样本点的响应值。由于在最佳基函数选择中需要对全基函数进行计算对比，因此初始样本点的数量一定要大于等于全基函数的项数，初始样本点的数量为：

k1≥(n+p)!/n!×p!

(1)

式(1)中：k1为初始样本点数量；n是函数的维数；p是函数的阶数。

2.2 响应面法

响应面函数设计思路应当形式简单，并使待定系数尽量少，以减小结构分析的工作量，因此在建立整体趋势函数时忽略交叉项。

考虑到实际工程问题需求，本文建立一至三阶不含交叉项的多项式作为备选趋势函数。一阶、二阶、三阶的响应函数为：

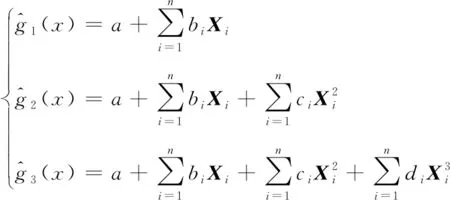
(2)

式(2)中，a、bi、ci和di为待定系数。

2.3 趋势判别

通过回归分析，计算出所有备选趋势函数的相关系数，选取趋势拟合程度最高的趋势备选函数的阶数作为Kriging模型中趋势函数的阶数。相关系数为：

(3)

选取相关系数最趋近于1的备选趋势函数的阶数作为Kriging模型中趋势函数的阶数。

2.4 最佳基函数选择

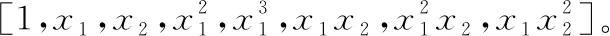
Martin等[14]开发的二进制编码非支配排序遗传算法，可以搜索基函数的最优子集。二进制编码的生成一个(n+p)!/n!×p!位编码，其中n是函数的维数，p是函数的阶数。全基函数中的每个多项式项都被分配给不同的编码。是否使用指定的多项式项由二进制数决定，其中1表示选择多项式项作为候选项，0表示没有选择多项式项。可定义目标函数为均方根误差最小，来比较每个基函数的适应值，通过迭代选择，直到满足收敛条件，即可从全基函数项中找到基函数的最佳子集。

2.5 主动学习函数及收敛条件

当基函数选取后，利用主动学习函数逐步增加具有重要意义的样本，进而更新已构建的Kriging模型，直至满足一定收敛条件。常见的学习函数有EEF函数、U函数和H函数。实践表明[15]，U函数和其他学习函数相比，在保持较高精度的同时，所需的样本数量较少，因此本文采用U函数，U函数的表达式为：

(4)

学习函数的停止条件(即Kriging模型的收敛条件)为：

min.(U(X))>2

(5)

2.6 基本流程

本文方法的基本流程如下：

1) 使用拉丁超立方抽样方式生成初始样本；

2) 通过响应面法求得一至三阶响应面函数，作为备选趋势函数；

3) 对所有备选趋势函数进行回归分析，分别计算对应R2值并判别，选取趋势拟合程度较高的备选趋势函数的阶数作为Kriging模型整体趋势函数的阶数；

4) 使用遗传算法搜索趋势函数的基函数最优子集，目标函数为均方根误差最小；

5) 通过主动学习函数训练已构建的Kriging模型，直至满足收敛条件。

3 算例

本文给出3个数值算例，包括三角函数、二维函数和三维函数，以验证本文提出的改进 Kriging模型(improved kriging model，IKM)的计算效率与计算精度。采用误差均方根衡量计算精度，采用总样本数量衡量计算效率，将IKM与经典Kriging模型(classical kriging model，CKM)、泛Kriging模型(universal kriging model，UKM)和趋势Kriging模型(trended kriging model，TKM)进行对比。计算表格中的UKM1代表一阶UKM、UKM2代表二阶UKM、TKM1代表一阶TKM、TKM2代表2阶TKM，k是样本的总数量。

k=k1+k2

(6)

式(6)中：k1是初始样本点的数量;k2是由主动学习函数筛选来的后续样本点数量。

3.1 测试函数1

测试函数1来源于文献[13]，有：

(7)

图1为测试函数1的真实响应值的等高线图，图2为本文方法给出的响应值等高线图。对比图1、图2可知，IKM的响应值与真实函数的响应值总体趋势吻合较好。

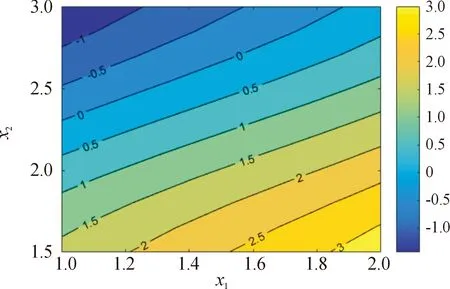
图1 测试函数1真实响应值等高线图

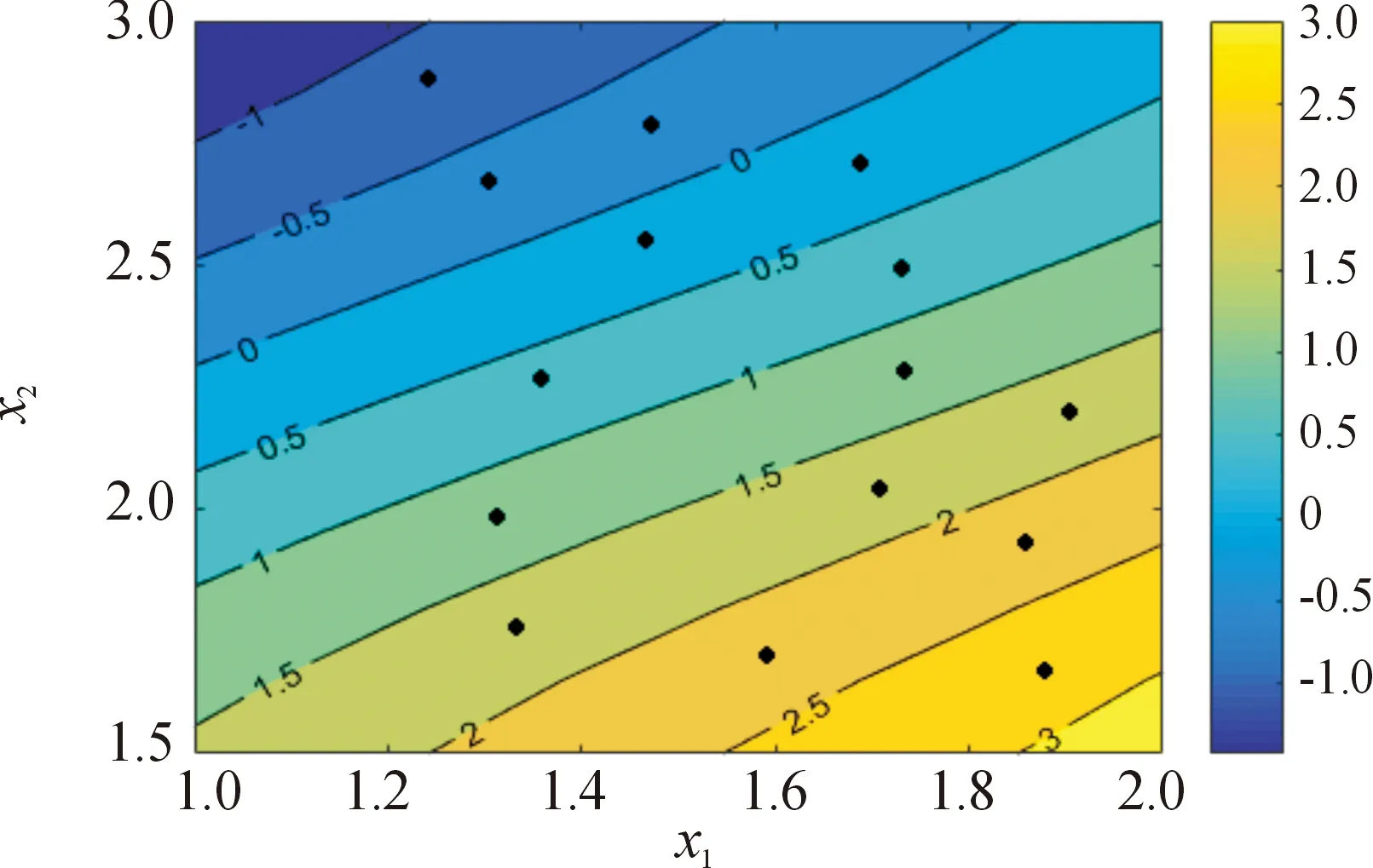
图2 基于IKM的测试函数1响应值等高线图

趋势函数计算结果见表1，IKM与其他模型的总样本数及对比见表2。通过表1可知，当代理模型整体趋势函数阶数等于2时，趋势拟合程度最高。由表2可知，本文算法需要12个初始样本和3个后续样本点，本文方法的计算效率和其他算法的计算效率相同，计算精度有显著提升。

表1 趋势函数的计算结果(测试函数1)

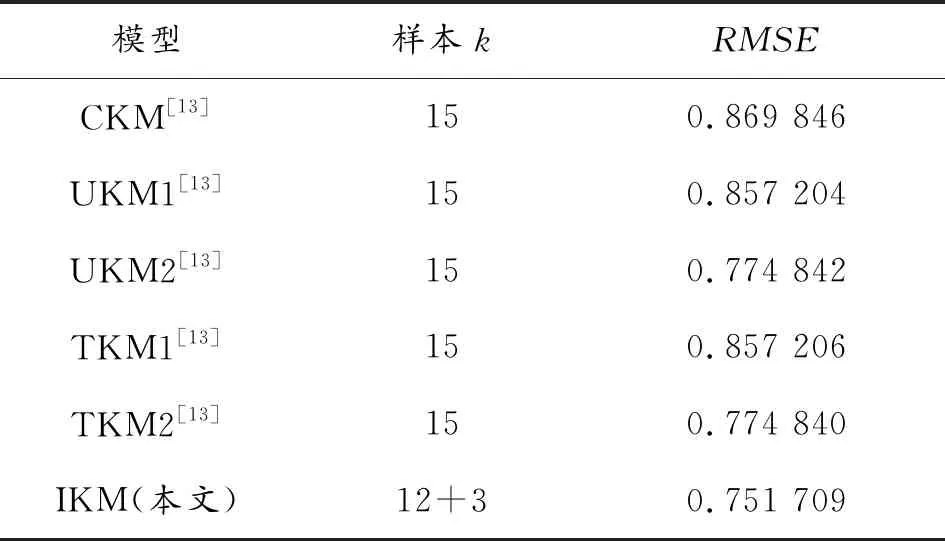
表2 各种计算结果(测试函数1)

3.2 测试函数2

测试函数2来源于文献[13]，有：

0.1(x1-3)2+0.1(x2-2)2

(8)

图3为测试函数2的真实响应值的等高线图，图4为本文方法给出的响应值等高线图。对比图3、图4可知，IKM的响应值与真实函数的响应值总体趋势吻合较好。

图3 测试函数2真实响应值等高线图

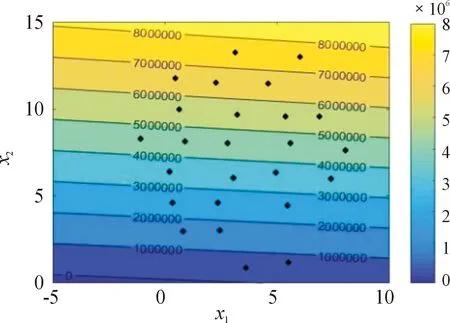
图4 基于IKM的测试函数2响应值等高线图

趋势函数计算结果见表3，IKM与其他模型的总样本数见表4。由表4可知，本文算法需要20个初始样本和5个后续样本点，计算效率比其他算法略低，但计算精度有显著提升。

表3 趋势函数的计算结果(测试函数2)

表4 各种计算结果(测试函数2)

3.3 测试函数3

测试函数3来源于文献[16]，有：

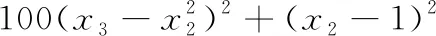
(9)

趋势函数的计算结果见表5，IKM与其他模型的总样本数见表6。通过表5可知，当代理模型整体趋势函数阶数等于3时，趋势拟合程度最高。由表6可知，本文算法需要40个初始样本和5个后续样本点，虽然计算效率比其他算法略低，但是计算精度有显著提升。

表5 趋势函数的计算结果(测试函数3)

表6 各种计算结果(测试函数3)

4 结论

在Kriging模型构建过程中，首先利用不含交叉项的多项式响应面法确定趋势函数的阶次，然后将趋势函数中忽略的交叉项重新加入Kriging模型的整体趋势函数中，通过遗传算法筛选趋势函数的基函数项，排除整体趋势函数中不必要的项，降低Kriging模型的计算量的同时提高模型的计算精度。

算例结果表明：由于本文考虑了整体趋势函数，在计算量增加不多的情况下，计算精度明显高于其他方法。然而值得注意的是，为了便于最佳基函数的选取，本文选取的初始样本点数量等于全基函数的项数，这将导致样本点数量随着变量个数的增加出现急剧增加的现象。对于这一问题，需对基函数选取方法进行完善，将在后续工作中进行改进。