无向拓扑多航天器系统分组姿态协同控制

王帅磊，周绍磊，代飞扬，刘玄冰

(海军航空大学， 山东 烟台 264001)

1 引言

姿态控制是多航天器系统控制中的重要问题之一。达到姿态协同是多航天器正常作业的前提，例如在多航天器对地观测、重力场测量等[1]场景中，都需要系统内航天器相互合作并保持相应的姿态。针对多航天器系统的姿态协同控制问题，文献[2]中采用SO(3)模型研究了带时滞的情况；文献[3]中引入了事件触发机制以减少系统内的通信；文献[4]考虑了复杂的约束条件；Liu等[5]针对领导-跟随结构的多航天器系统展开了研究；Lu和Liu进一步考虑了切换拓扑的情况[6]；现有研究还针对带有避撞约束[7]、惯性不确定性[8]以及存在时滞[9]的情况进行了分析。

现有研究大多致力于使多航天器系统中所有航天器的姿态收敛到同一个固定的或时变的姿态，而在较为复杂的应用场景中，将整个系统划分为多个分组进行控制是必要的，例如在SAR卫星编队的协同监控[9-10]中，需要编队中的卫星保持不同的姿态。对于这种分组情况，Weng等[11]在SO(3)模型上结合事件触发机制研究了多个分组的姿态协同控制问题，而该研究中需要对每个分组设定领导者。文献[12]采用修正罗德里格斯参数(modified rodrigues parameters，MRP)描述刚体姿态，并直接利用姿态和角速度信息设计了控制输入，该研究中引入了分组一致的概念。分组一致是指，系统中所有个体的状态量能够同时收敛到多个固定值或时变值。这意味着系统可以划分为多个分组，每个分组内部都能达到一致。关于分组一致的研究主要集中在基于质点模型的多智能体系统[13-16]。在文献[12]的基础上，文献[17]进一步将分组姿态协同控制问题扩展到了有向拓扑结构，采用了一种变量代换和矩阵分解相结合的方法，解决了切换拓扑条件下的分组姿态协同控制问题。总体上，目前针对多航天器系统的分组姿态协同控制研究仍然较少。

将多航天器系统划分为多个分组进行控制，可以直接将系统分割为多个孤立的子系统，并分别设计控制输入，但这将破坏系统的整体性，同时增加了控制量，控制难度也随之增加。而通过引入分组一致性理论中的入度平衡[18]条件，不需要对系统进行分割，在保持系统整体性的同时，仅需要设计一种控制输入，就能够实现系统内状态量的分组一致，即多航天器的分组姿态协同，因此这一控制方法更具优势。

本文基于分组一致相关理论，通过构造辅助变量，设计了分布式的控制输入，对无向拓扑上的多航天器系统分组姿态协同控制问题进行了研究。本文其余内容安排如下：第1节中构建了基于无向图的多航天器系统；第2节构造了辅助变量，并设计了分布式的控制输入，对多航天器系统的稳定性进行了分析；第3节中对包含4个分组的多航天器系统进行了仿真；第4节给出了本文的结论。

2 多航天器系统构建

2.1 航天器姿态动力模型

考虑一个由N个具有相同运动特性的航天器组成的多航天器系统，并且该系统可划分为s个分组。每个分组中航天器的数量为ni，并且每个航天器仅能够被划分到唯一的分组中。若航天器i属于分组gj，那么存在映射Γ(i)=gj。采用MRP描述航天器的姿态，第i个航天器的姿态运动学和动力学方程可以记为：

(1)

式(1)中：σi(t)∈R3、ωi(t)∈R3和ui(t)∈R3分别表示MRP参数下航天器的姿态、角速度和控制输入；正定对称矩阵J∈R3×3表示航天器的转动惯量。Gi(t)定义为：

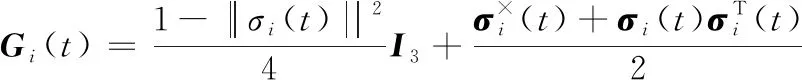
(2)

其中

(3)

2.2 多航天器系统通信拓扑

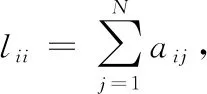
由于本文中多航天器系统是分组的，因此基于现有关于分组一致的研究，本文采用如下假设。

假设1：系统通信结构为无向拓扑，若2个分组之间存在边，则这些边满足入度平衡[18]。对于分组si和sj，存在节点vk1,vk2∈si和节点vk3,vk4∈sj，使得邻接矩阵中ak1k3=ak2k4=1，并且ak1k4=ak2k3=-1。

假设2：L的非零特征值均为正实数。

定义1：称多航天器系统达到分组姿态协同，当且仅当同一分组中的航天器i和航天器j满足：

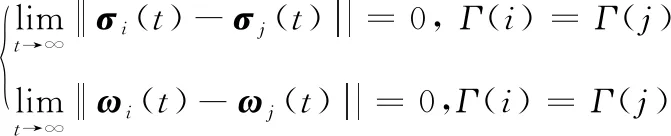
(4)

那么本文的研究目的可以描述为：设计一种控制输入，使无向拓扑上的多航天器系统达到如式(4)描述的分组姿态协同。

3 控制器设计

3.1 分布式姿态控制器设计

为了便于表示，后续分析中将省略时间符号t。

首先，对航天器构造辅助变量，即：

(5)

式(5)中，参数μ>0。于是可知：

(6)

即多航天器系统的分组姿态协同问题转化为了辅助变量si的分组一致问题。根据式(5)，得到：

(7)

从而可以设计控制输入为：

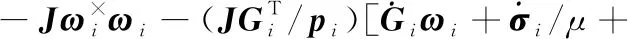
(8)

由于每个航天器的控制输入中仅利用了邻居的姿态和角速度信息，因此控制输入是分布式的。根据假设1可知：

(9)

因此对于航天器i，有如下等式成立，即：

(10)

将式(10)代入式(8)，可以得到：

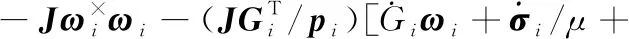
(11)

对式(11)进行化简，得到：

(12)

结合式(7)和式(12)，可知：

(13)

从而根据式(13)得到多航天器系统的闭环方程为：

(14)

记分组gk中所有辅助变量的均值为：

(15)

并对该均值求导可知：

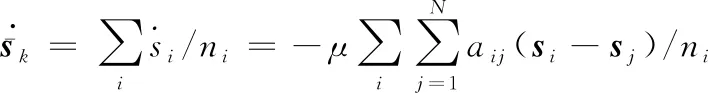
(16)

由于Laplacian矩阵是对称矩阵，因此有：

(17)

这意味着每个分组内辅助变量的均值是时不变的常值。因此，若每个分组初始时刻辅助变量的均值互不相同，且系统能够达到分组姿态协同，那么最终各个分组的协同姿态和协同角速度仍将保持互不相同。

3.2 稳定性分析

定理1若通信拓扑为无向拓扑的多航天器系统满足假设1和假设2，那么给定如式(8)的控制输入，多航天器系统能够达到分组姿态协同。

证明选定Lyapunov函数为：

V=sTs/2

(18)

显然有V≥0成立。

对Lyapunov函数V沿式(14)求导，得到：

(19)

Ω={s|sTL⊗I3s=0}

(20)

即系统(14)是渐近稳定的。而sTL⊗I3s=0意味着s=0或者L⊗I3s=0。当s=0时，有：

s1=s2=…=sN=0

(21)

而根据si=0可知：

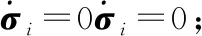
由于L1N=0成立，因此当L⊗I3s=0时，有：

Ls1=Ls2=Ls3=0

(22)

式(22)中，s1、s2和s3分别为向量s在第1、第2和第3个方向上的分量。即：

(23)

因此可知若Γ(i)=Γ(j)，那么将有

si=sj

(24)

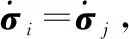
综上所述，在本文设计的控制输入作用下，多航天器系统能够达到分组姿态协同。证毕。

4 仿真结果与验证

多航天器系统的无向通信拓扑如图1所示。

以一个包含19个航天器与4个分组的系统为例，基于MATLAB平台进行仿真。其中航天器1～4组成分组g1，航天器5-8组成分组g2，航天器9～14组成分组g3，航天器15～19组成分组g4。根据图1可以确定，在邻接矩阵A中，元素a15=a26=-1，a16=a25=1，a710=a89=-1，a79=a810=1，a1215=a1314=-1，a1214=a1315=1。因此，多航天器系统的无向通信拓扑满足入度平衡。

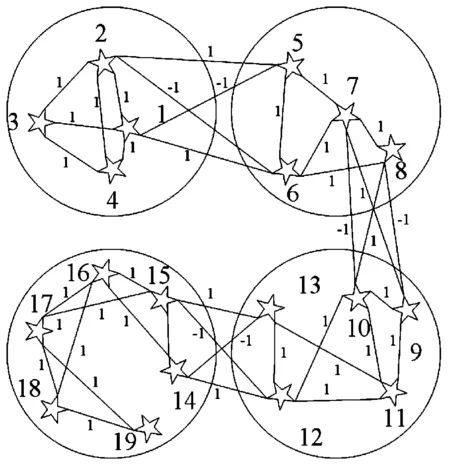
图1 多航天器系统的无向通信拓扑示意图

设定航天器的转动惯量矩阵J=I3，仿真时长共100 s，并设定参数μ=1。航天器的姿态时间响应和角速度时间响应分别如图2和图3所示。纵坐标的上角标1、2和3表示第1、第2和第3个方向上的分量，下角标i表示航天器的编号。

根据图2结果可知，分组g1和分组g2中，航天器的姿态分别达到了协同，并且2个分组的协同姿态并不相同。在3个分量上，2个分组的协同姿态各自稳定在一个常值。

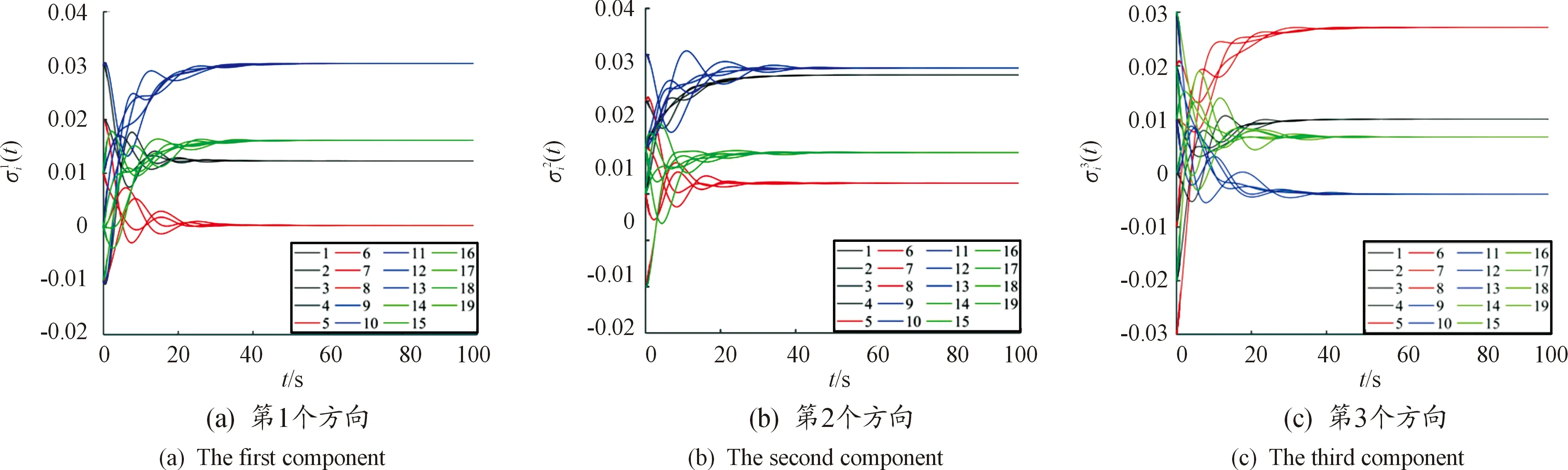
图2 航天器的姿态时间响应曲线在3个方向上的分量

根据图3结果可知，分组g1和分组g2中，航天器的角速度都收敛到零，这意味着最终多航天器系统是静态的。

图3 航天器的角速度时间响应曲线在3个方向上的分量

图2和图3的结果表明，在本文给定的控制输入作用下，多航天器系统达到了静态的分组姿态协同。

与本文基于滑模变量提出的控制输入不同，文献[12]直接利用姿态和角速度信息设计了控制输入。采用同样的拓扑结构和初始条件，对文献[12]提出的控制输入进行仿真复现，与本文提出的控制输入进行比较。

图4表明，在文献[12]控制输入作用下，多航天器系统中2个分组的姿态也能够分别达到协同，并且协同姿态是时变的。

图4 航天器的姿态时间响应曲线在3个方向上的分量(文献[12]提出的控制输入与本文提出的控制输入)

图5表明，2个分组的角速度也分别达到了协同，并且协同角速度均不为零，即多航天器系统最终达到了动态的分组姿态协同。

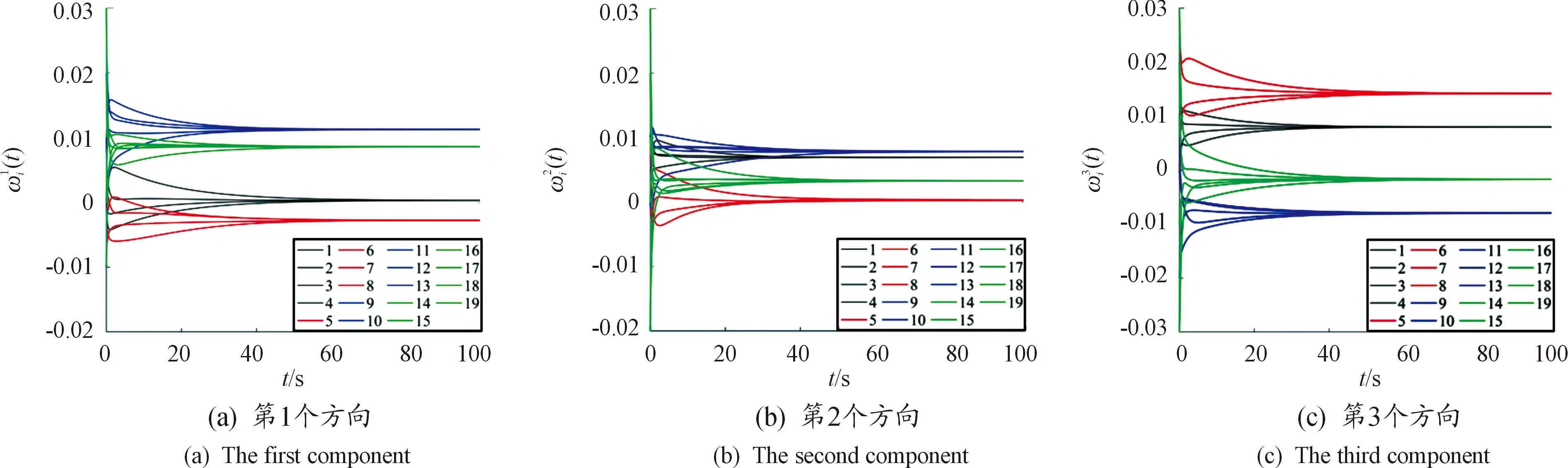
图5 航天器的角速度时间响应曲线在3个方向上的分量(文献[12]提出的控制输入与本文提出的控制输入)

对于以卫星编队为代表的多航天器系统来说，由于大多数时候需要卫星保持在期望的姿态以朝向地面，因此静态的分组姿态协同相比动态的分组姿态协同更具有现实应用意义。

通过对比图2、图3和图4、图5可知，在控制效果上，本文及文献[12]的控制输入都能够使多航天器系统达到分组姿态协同。从最终的协同姿态和协同角速度来看，文献[12]中的控制输入能够使多航天器系统达到动态的分组姿态协同，而本文的控制输入能够使多航天器系统达到静态的分组姿态协同，更贴近工程应用需求；从达到分组姿态协同的速度来看，本文提出的控制输入能够使系统更快达到分组姿态协同，控制效率上更具优势。

5 结论

1) 通过设计辅助变量，能够将分组姿态协同控制问题转化为分组一致问题；

2) 本文提出的控制输入是分布式的；

3) 本文提出的控制输入能够使多航天器系统达到静态的分组姿态协同，并且在控制效率上更具优势。