基于PSO-Powell混合算法的软磁复合材料二维矢量磁滞特性模拟

赵小军 徐华伟 刘小娜 李永建 杜振斌

（1.华北电力大学电力工程系 保定 071003 2.西安华为技术有限公司 西安 710075 3.河北工业大学电磁场与电器可靠性省部共建重点实验室 天津 300130 4.河北省输变电装备电磁与结构性能重点实验室 保定 071056）

0 引言

近年来，软磁复合材料（Soft Magnetic Composite, SMC）因其独特的电磁性能被大量应用于电机及电力电子设备中。与传统电工硅钢材料相比，SMC材料具有磁热各向同性、中高频涡流损耗低、加工形状多样化、制造成本低等优点[1-2]，更有利于复杂电磁结构的关键设计和三维磁路拓扑结构的开发，在电枢式爪极电机、横向磁通电机等电磁设备中得到广泛的应用[3-5]。磁滞现象是磁性材料固有的重要特征，其复杂的非线性磁滞特性对电气设备的优化设计及运行特性分析具有十分重要的影响。因此，针对 SMC材料磁滞特性的准确测量和模拟成为其研究应用的关键[6-7]。

传统的标量磁特性模拟只能体现软磁材料在交流激励下的磁特性，然而在实际工程中，旋转电机定子及电力变压器铁心拐角处通常运行在交变与旋转磁化激励下[8]，此时磁场强度和磁通密度并非总是沿着同一方向，且由旋转激励引起的损耗大于单方向的交变损耗[9-11]。因此，在实际应用中，相关研究者更关注 SMC材料在旋转激励下的矢量磁滞特性[12-13]。

国内外许多学者利用一些最新开发的测量方法[14]提出了不同的矢量磁滞模型。E.C.Stoner和E.P.Wohlfarth提出一种矢量滞后模型[15]，该模型设计为具有对称回环的单畴单轴磁滞算子磁特性的矢量叠加和，因此无法拟合非对称磁滞小回环，并且还未完全实现计算模型分布函数的参数辨识。基于上述缺点，I.D.Mayergoyz提出了经典矢量Preisach模型[16]，可用于拟合二维和三维材料的各向同性磁滞特性，该模型在磁滞建模中具有明确的物理意义及精准的拟合效果，因此被广泛应用于电磁计算当中。然而，大量实验表明，与交流激励下 SMC材料呈现出的各向同性磁特性不同，在旋转激励下，材料将呈现出部分各向异性[17-18]。因此，经典矢量Preisach模型不再适用，需要进一步改进。M.Kuczmann在此基础上提出了基于神经网络的改进矢量Preisach模型及其模型参数辨识的方法[19-20]，使其可考虑材料的部分各向异性特征，该模型仅通过引用方向角的关联参数来改善磁场强度曲线形态，在较低磁通密度幅值下的拟合结果误差较大。此外，M.Enokizono和 N.Soda提出考虑旋转磁化的 E&S矢量磁滞模型[21]，该模型针对旋转激励条件下较明显的各向异性磁特性拟合，但由于模型中包含众多参数，需要大量实验数据拟合得到，严重地限制了其应用。

本文利用矢量磁特性测量平台[22]，对 SMC材料在旋转激励下的二维磁滞特性进行测量和分析。通过在经典矢量磁滞模型中引入幅值及方向角的关联参数改善曲线形态，提出一种能够考虑 SMC材料各向异性特征的改进矢量Preisach模型。基于不同方向的极限磁滞回线，采用数值方法生成一阶回转曲线（First Order Reversal Curves, FORCs），构造标量和矢量 Everett函数，将粒子群优化（Particle Swarm Optimization, PSO）算法和Powell方向加速法相结合，提高了参数提取精度及计算效率，进而实现Preisach矢量磁滞模型的高效参数辨识。测量结果与仿真结果的对比和分析验证了本文所提方法的有效性。

1 SMC材料二维磁滞特性测量

矢量磁特性测试系统结构框图如图1所示，三维磁特性测试系统主要由主测量装置、功率放大器、差分放大电路和数字信号处理单元组成，其中，由铁心搭建而成的主测量装置是整个测量系统的核心，它主要包括C形磁极、励磁绕组和B-H复合传感线圈。为了保证样品在给定频率下被充分磁化，三路模拟励磁信号分别经三路功率放大器和阻抗、谐振匹配电路选频，获得比较大的励磁电流，作为励磁绕组的输入信号，从而使磁极心结构在测量样品内部生成旋转磁场；样品上的传感线圈感应到微弱的电信号，该信号经差分放大电路输入到数字信号处理单元中，实现B、H检测信号的采集，经Labview软件进行数据的收集，从而实现系统的闭环运算和反馈。

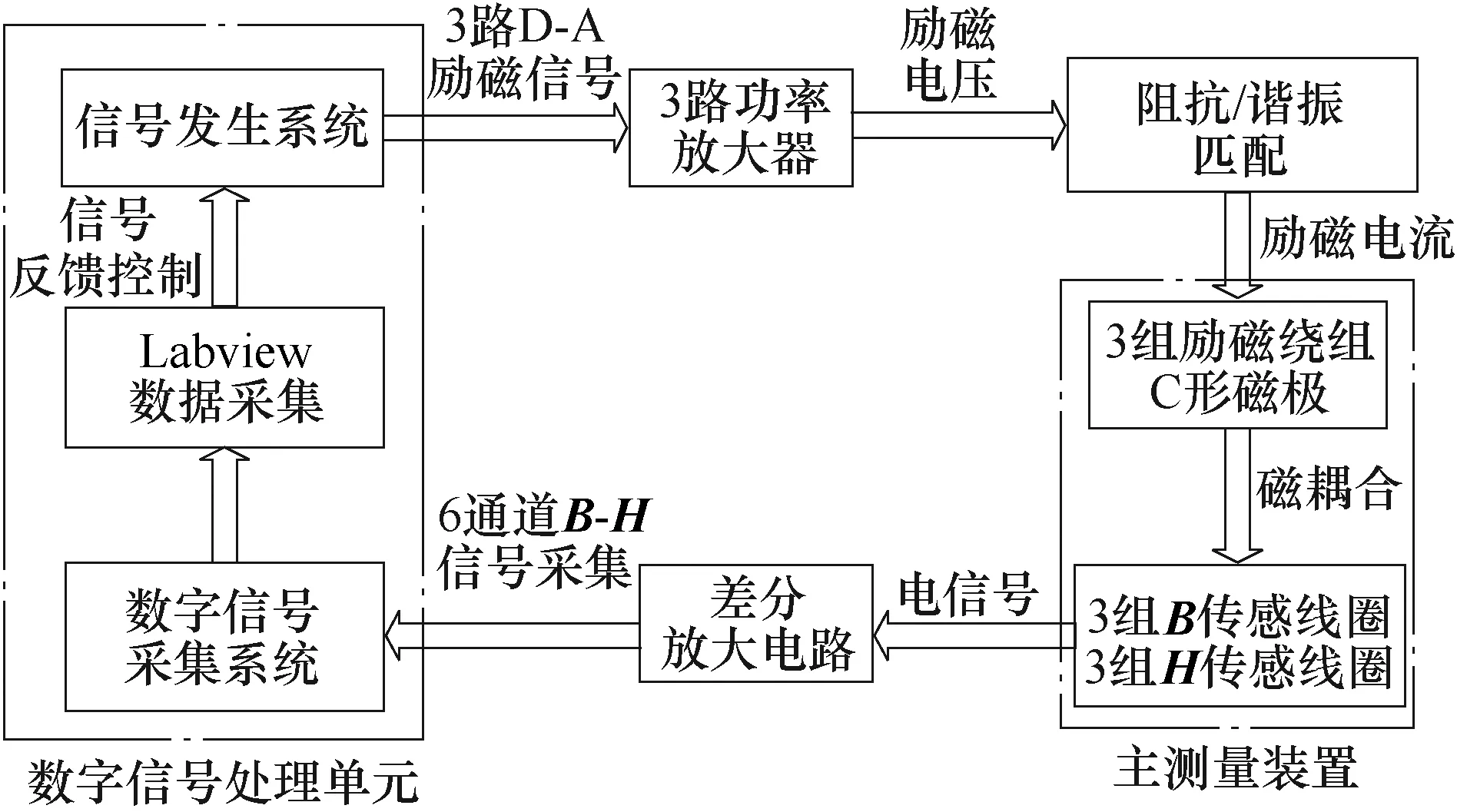
图1 矢量磁特性测试系统结构框图Fig.1 Block diagram of vector magnetic property testing system

利用该测量系统对型号为SOMALOY 500（由瑞典Höganäs公司研制）的软磁复合材料进行二维磁特性测量，该样品在电场强度为100kA/m时的最大磁通密度为 2.1T，剩磁为 0.25T，矫顽磁力为250A/m，电导率为 30μΩ·m，热导率为 17W/(m·K)，初始相对磁导率为 130。在实验过程中，样品被切割为边长为22mm的立方体，放置于高精度B-H复合立方体传感箱内，传感箱六面贴装高精度B-H复合传感线圈，实现B、H的测量，图2a、图2b分别为主测量装置实体及主磁路模型。

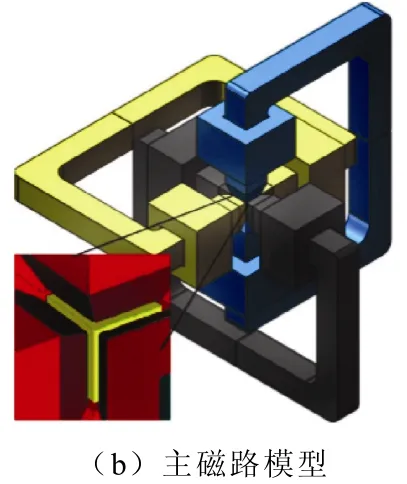
图2 三维磁特性主测量装置Fig.2 Main device of 3-D magnetic property measurement

为保证矢量磁通密度B的二维平面轨迹为圆形，在xOy平面上施加低频（f =5Hz）圆形旋转激励，通过改变励磁电流大小，测量了B、H二维低频矢量磁滞曲线，如图3和图4所示。由实验特性图可以看出，随着励磁电流的增大，与圆形B轨迹对应的H轨迹逐渐呈现出椭圆和类似花瓣的曲线形态，SMC材料对外表现出部分磁各向异性特征。

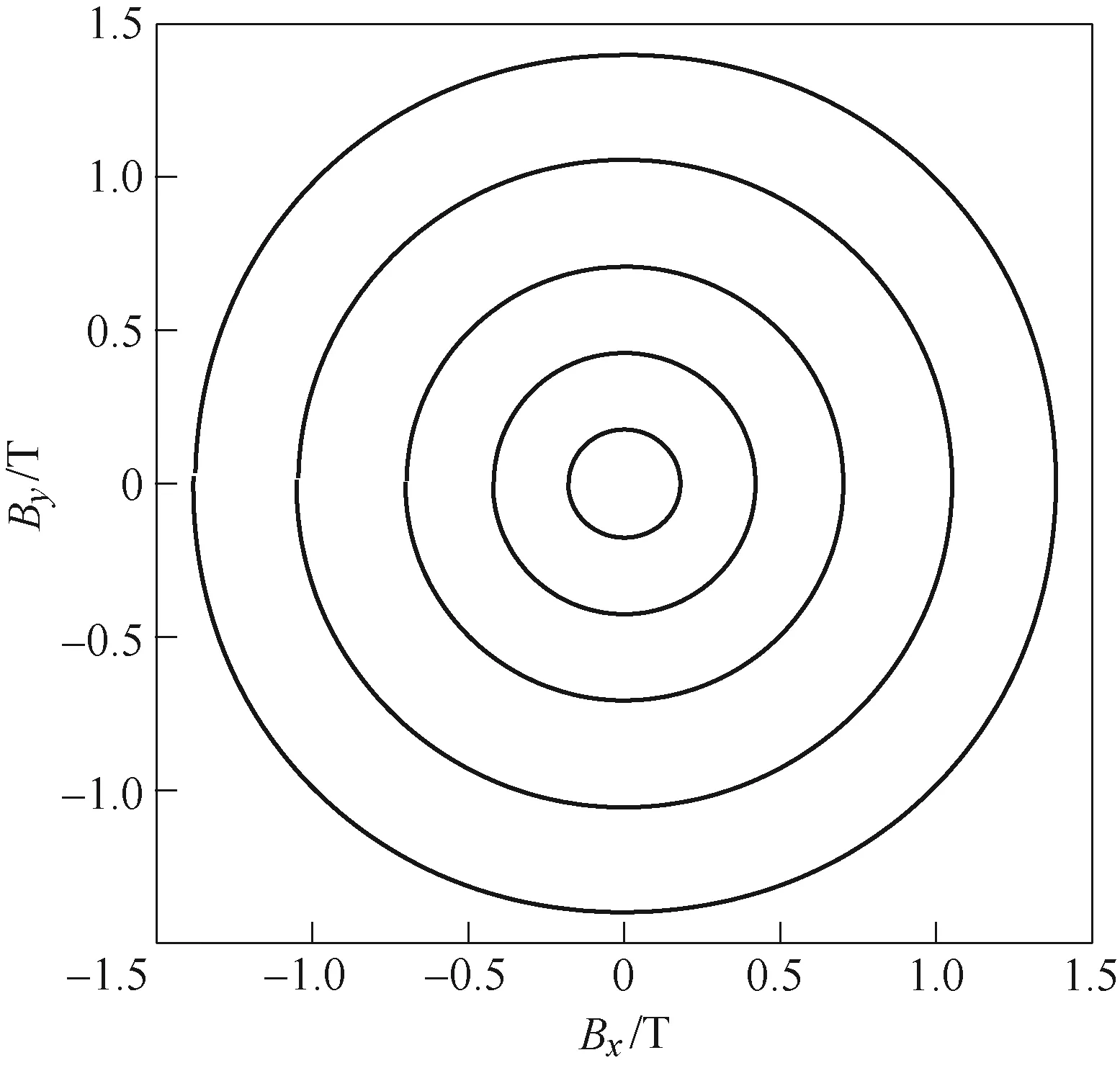
图3 矢量B空间轨迹Fig.3 The loci of vector B

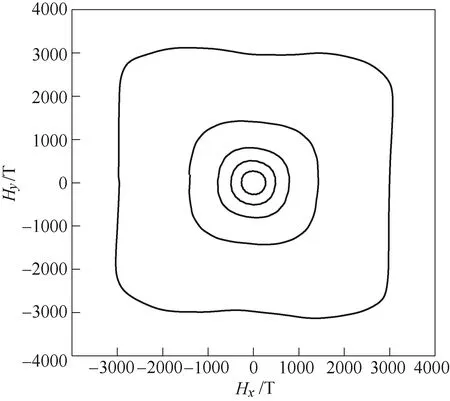
图4 矢量H空间轨迹Fig.4 The loci of vector H

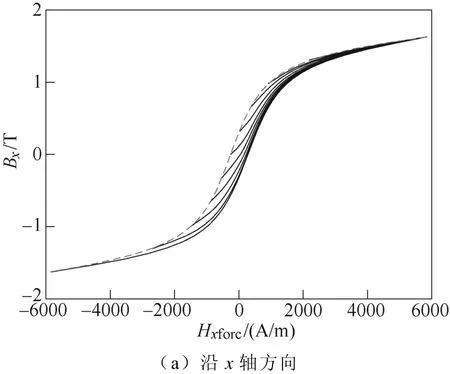
图5a和图5b分别为沿x、y轴方向同心磁滞回环的测量曲线，其中，饱和磁通密度对应的磁滞曲线即为本文所需的极限磁滞回线。

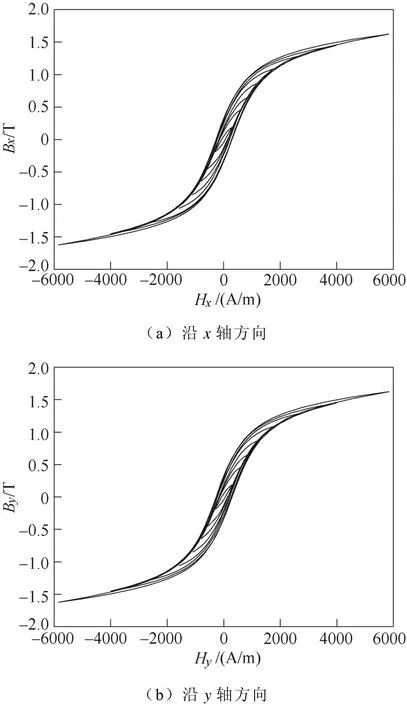
图5 同心磁滞回环Fig.5 Measured concentric loops

2 改进的矢量Preisach模型

2.1 基于经典矢量Preisach模型的改进

采用二维经典矢量Preisach模型的逆形式，即以磁通密度B为输入求解磁场强度H的表达式[16]为

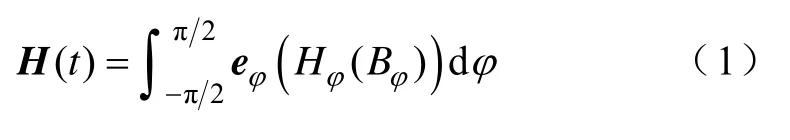
式中，Bφ为矢量B(t)沿φ方向的标量磁通密度；Hφ(Bφ)为H(t)沿着eφ方向的标量磁场强度。

在磁场的数值计算过程中，将区间φ∈[−π/2, π/2]均匀分成n个小区间，即

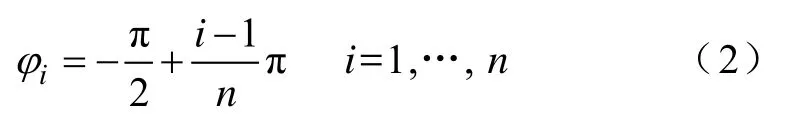
式中，n为方向的个数；i为各方向的编号。

因此式（1）中的矢量磁场强度可表示为标量磁场强度在各个方向的矢量和，有

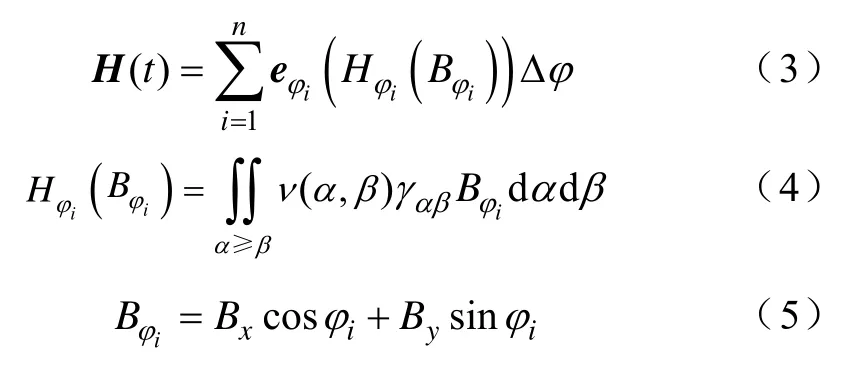
式中，Hφi(Bφi)为H(t)沿φi方向的标量磁场强度；Δφ为区间间隔，Δφ=π/n；α和β分别为输入的正、负向翻转阈值；γαβ为由α和β控制的磁滞算子；ν(α,β) 为矢量Preisach分布函数；Bx和By分别为沿x和y方向的标量磁通密度。

为避免式（4）中关于α和β的双重积分，通常采用数值的方法，利用矢量Everett函数E[16]实现矢量Preisach模型的参数辨识。E的具体表达式为

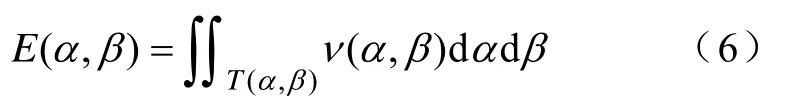
式中，T(α,β)为Preisach平面中被α和β包围的三角形。

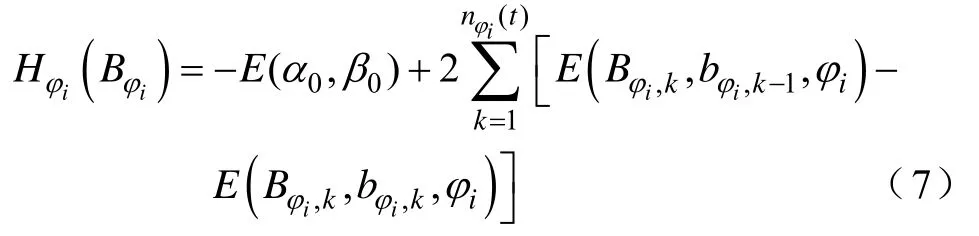
式中，α0和β0分别为正、负向磁通密度饱和值；Bφi,k和bφi,k−1分别为输入磁通密度B沿eφi方向一系列的最大值和最小值；nφi(t)为沿φi方向的一阶回转曲线的回转点个数。

矢量 Everett函数E可以与标量 Everett函数F联系起来，有

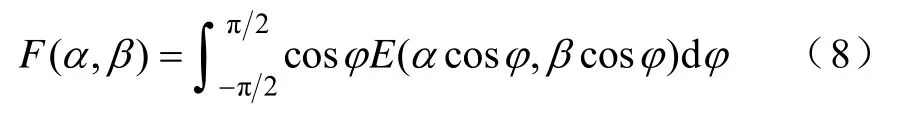
式中，F(α,β)与E(αc o sφ,βc o sφ)分别为可由测量数据通过数值方法生成的标量 Everett函数和未知的矢量Everett函数。

以上给出的是经典矢量磁滞模型，其特性如下：当输入为如图3所示的基于磁通密度B的均匀旋转激励时，模型输出的磁场强度H轨迹为圆形[23]。然而由第1节所述实验可知，对SMC材料施加基于B的均匀旋转激励时，输出H的轨迹实际上并非圆形，而是不规则的环状，略微呈现类似花瓣的形态如图4所示。这是由于SMC材料本身仍具有一定的磁各向异性。显然，此时利用经典矢量磁滞模型无法对其磁特性进行准确模拟。

为此，本文提出以下策略，对模型进行改进，使其能够考虑上述磁各向异性对旋转磁滞特性的影响。引入与方向角、幅值相关联的两个参数w和z来改善矢量H的曲线形态，其中，参数w通过控制H沿各离散方向的投影使模型能够呈现部分各向异性，参数z用于调整H的幅值[24]。改进模型的具体表达式为

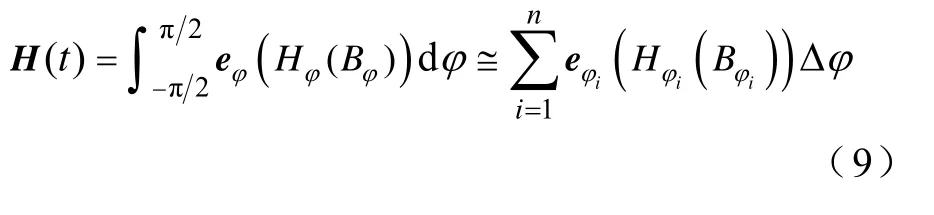
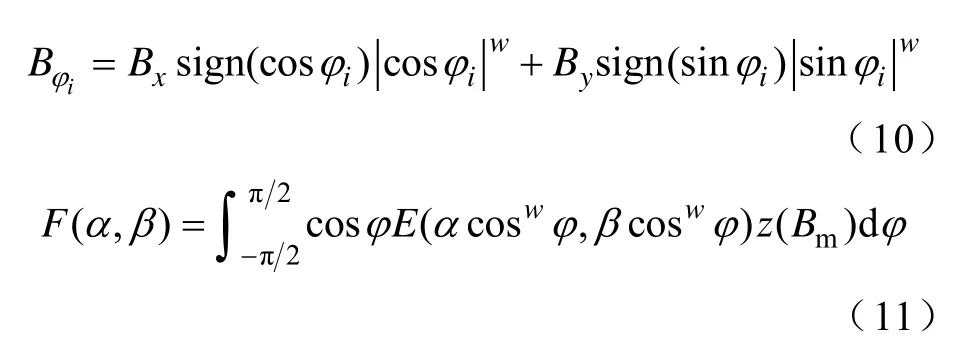
式中，Bm为输入B的幅值。

当0＜w＜1时，该模型可以模拟材料的部分各向异性特征，使输出H的轨迹由圆形变为椭圆或者略呈花瓣形状；不失特殊性，当w=1时，模型即为经典矢量模型。此外，引入参数z使模型对不同Bm下矢量 Everett函数的幅值进行调整，进而调整H的幅值，从而使得拟合结果更加准确。

输出磁场强度沿x方向和y方向的分量分别为

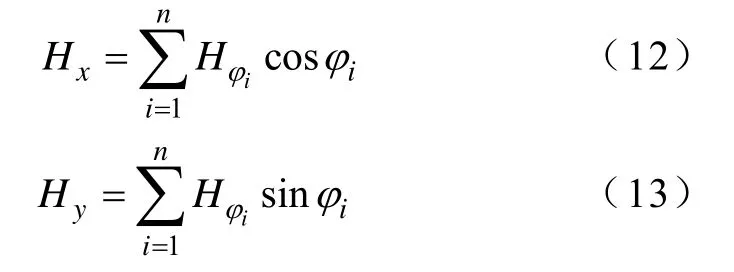
2.2 改进矢量Preisah模型的参数辨识

由式（8）可知，利用函数F能够实现对改进模型中矢量E函数的参数辨识。在数值计算过程中，将此式写成数值累加和的形式[25]，有

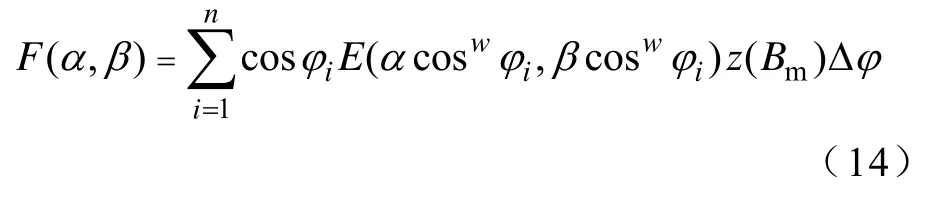
式中，F可以通过实验测量得到，也可以利用数值的方法生成，本文根据测量的极限磁滞回线数据结合数值方法实现F的参数辨识。

利用图5中x、y方向极限磁滞回线下降支的实验数据，采用 Dlala提出的数值方法生成的一阶回转曲线[26]如图6所示。沿x、y轴方向生成的一阶回转曲线略有差异，使得材料表现出轻微的各向异性特征。

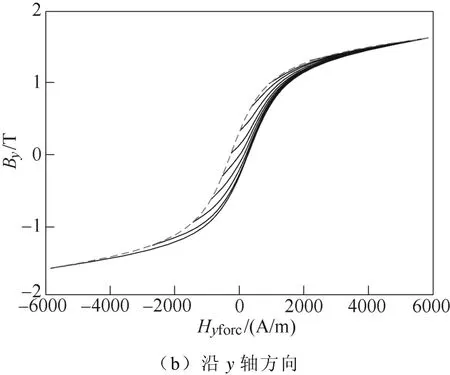
图6 一阶回转曲线Fig.6 First order reversal curves

根据文献[16]中给出的数值方法，x、y方向上的标量 Everett函数Fx、Fy可通过数值生成的一阶回转曲线插值求得，有

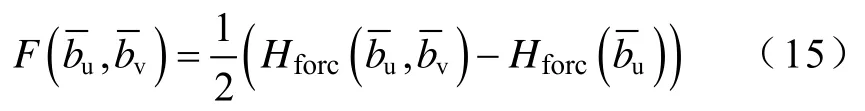
如图7所示分别为x、y轴方向一阶回转曲线生成的标量Everett函数Fx、Fy。

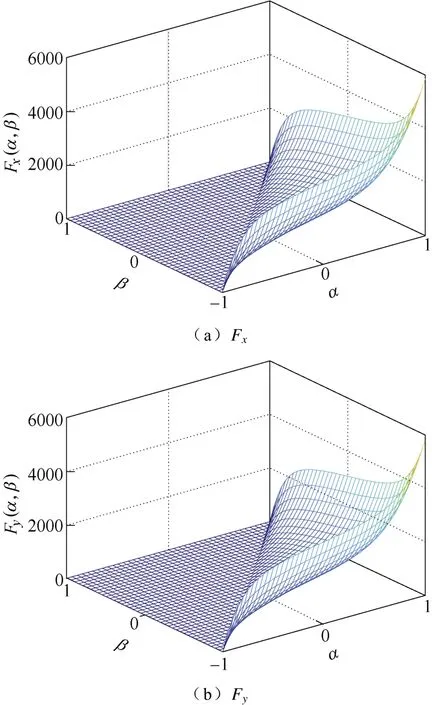
图7 沿 x、y方向上的标量Everett函数 Fx、FyFig.7 Normalized inverted scalar Everett function Fx, Fy constructed from FORCs

在圆形旋转激励下，标量 Everett函数F可表示[19]为

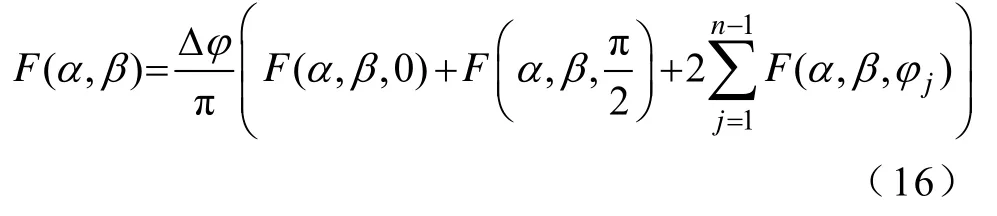
式中，F(α,β,φ)为对x、y方向上标量Everett函数Fx、Fy的椭圆插值，有

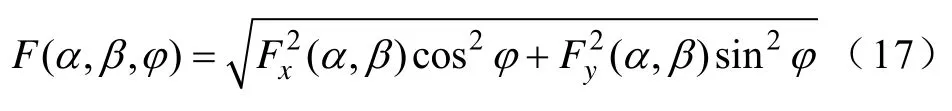
由此，根据图7中生成的Fx、Fy，由式（16）、式（17）可得模型的标量Everett函数F如图8所示。

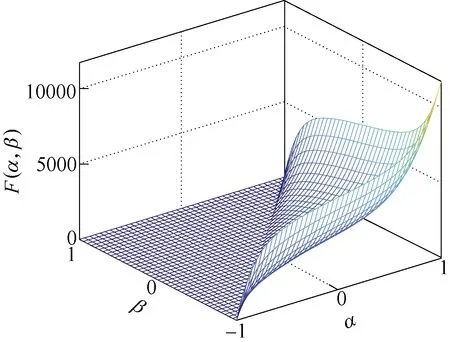
图8 标量Everett函数FFig.8 Scalar Everett function F

由式（14）可知，Bm、w、z给定的情况下，根据所得的F函数便可生成E函数，假设Bm=1.398T，w=0.7，z=2，得到的函数E如图9所示。

图9 矢量Everett函数EFig.9 Vector Everett function E

3 基于改进模型的SMC材料二维磁滞特性模拟

3.1 基于PSO与Powell混合优化算法的改进模型参数提取

通过引入参数w、z可以模拟SMC材料的部分各向异性，因此，如何提取这两个参数成为改进矢量模型应用的关键。本文综合随机性优化算法全局搜索能力强与确定性优化算法局部寻优能力强的各自优势[27]，提出一种基于 PSO与Powell混合优化算法的改进矢量模型参数提取方法，以此实现参数的精确快速提取。

为对参数提取的精度进行准确评价，本文选取实验值与拟合值的平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）作为目标函数，将改进矢量Preisach模型的参数优化问题转化成了求目标函数最小值问题。

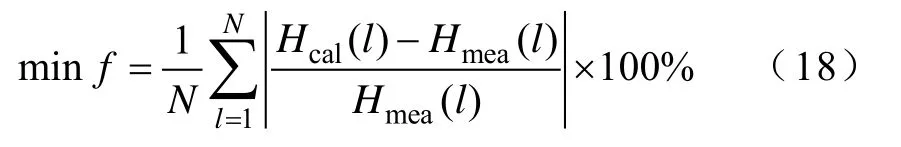
式中，f为目标函数；Hcal、Hmea分别为磁场强度拟合、测量值；N为实测数据的个数。

本文首先选取PSO算法来进行全局寻优，该算法具有较强的全局收敛性和稳健性，能以较快的速度到达全局最优解所在区域[28]，具体步骤如下：

（1）初始化种群，在二维求解空间中随机生成粒子位置和速度，待求参数w、z作为粒子位置X的自变量，即X=X(w,z)。选定种群规模N=5，各初始粒子j的位置其中[1, 1.5]，初始化粒子速度范围[0, 0.3]，初始迭代次数k=1，加速因子c1=c2=0.3，惯性因子ω=1。

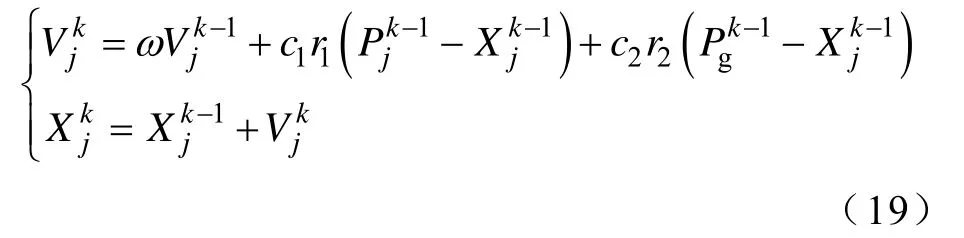
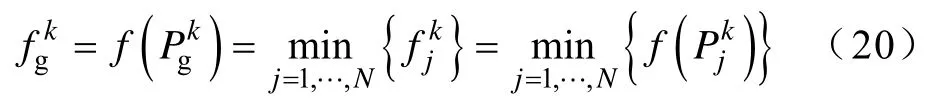
为充分发挥算法全局寻优与局部寻优的优势，提高计算效率，确定 PSO算法与 Powell算法的优化衔接准则为

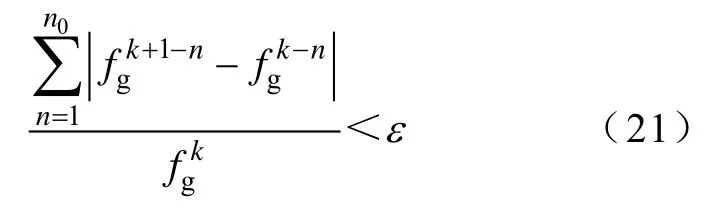
式中，n0为连续多次迭代次数，本文中选取n0=10，ε=0.01。

基于本文中目标函数的复杂性，考虑到Powell算法无需进行对目标函数求偏导的复杂操作，并且具有较强的局部搜索能力，本文采用该算法对矢量Preisach模型参数进行局部寻优，具体过程如下：

（1）以当前PSO算法的最佳解决方案为Powell算法的初始基点设置初始迭代轮次t=1，迭代精度为0.001，初始搜索方向组

（4）判断是否满足迭代终止条件。若满足，则输出当前最优解及对应最优目标值f(x*)；否则执行步骤（5）。

（5）计算第t次迭代中每相邻两点目标函数值的下降量，并找出最大下降量及其相应方向，有

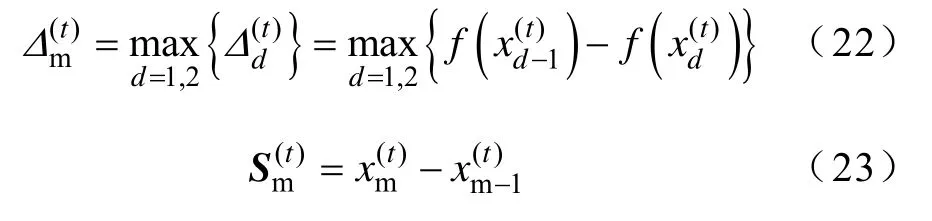
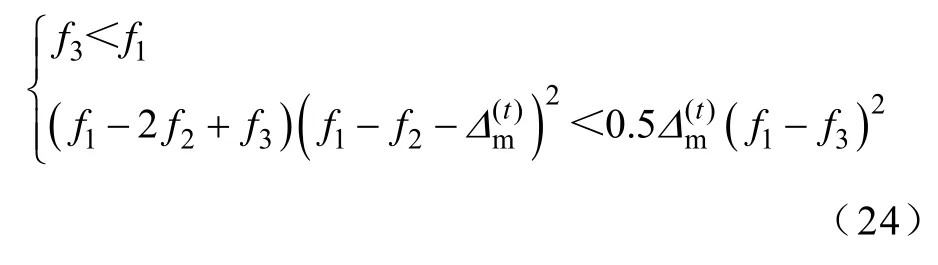
沿S(t)方向计算映射点令f1=若满足 Powell条件，有则设置下一轮迭代初始点，并用S(t)方向取代，t=t+1，转步骤（2）；否则转步骤（6）。

（6）若满足f2＜f3，则选取下一轮迭代初始点转步骤（2）；否则取t=t+1，转步骤（2）。

结合PSO-Powell混合算法，由改进矢量Preisach模型对SMC材料（SOMALOY 500）在圆形旋转激励下的矢量磁滞特性进行准确快速模拟，具体拟合过程如图10所示。

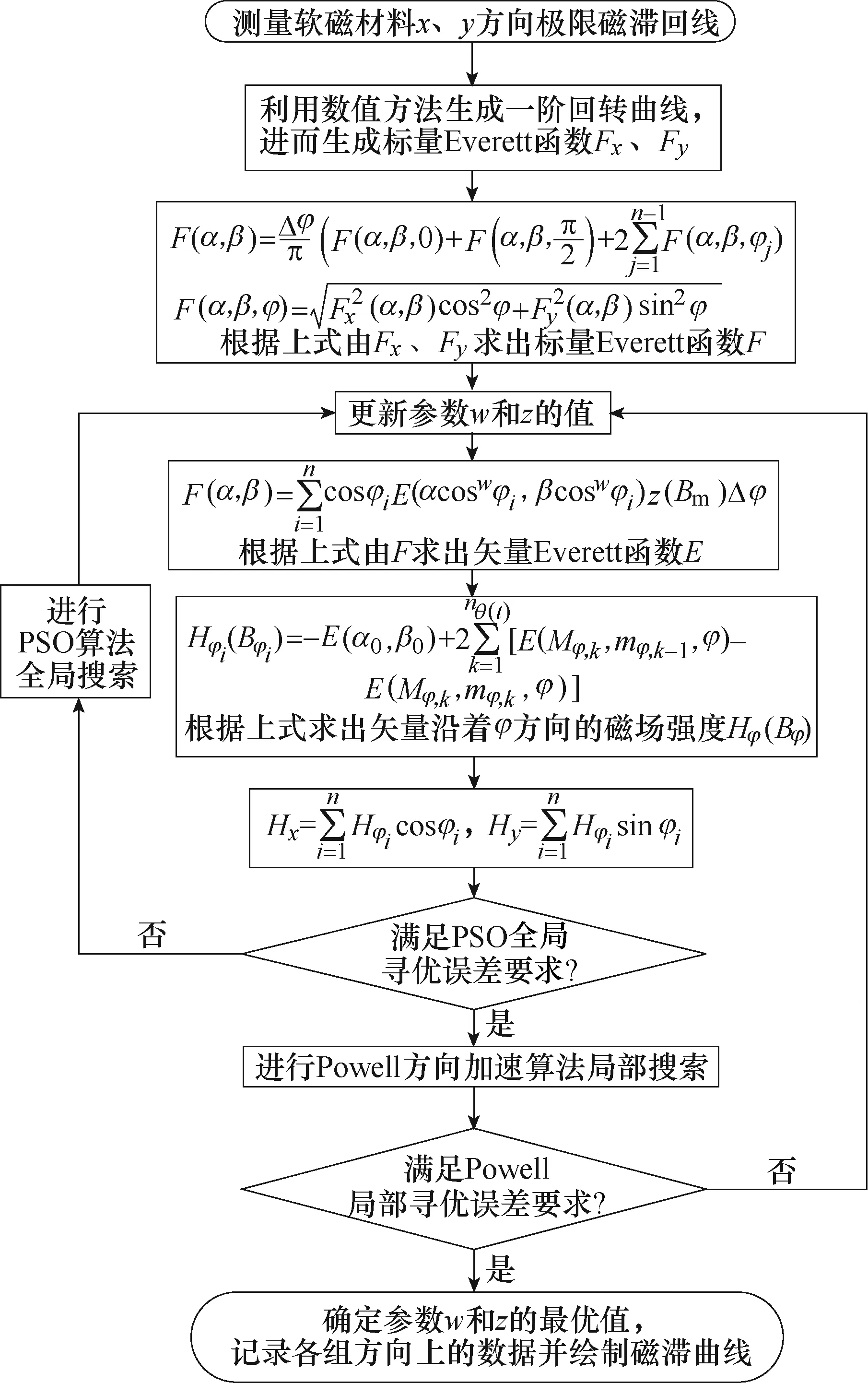
图10 改进矢量Preisach模型拟合过程流程Fig.10 Flow diagram of simulation process

3.2 软磁材料二维磁特性拟合结果

为便于直观比较，对PSO算法与混合算法赋予相同范围的初始值及寻优速度；同时，以式（21）为PSO算法的迭代终止条件，但最大迭代次数不超过100，而混合算法的迭代终止条件由Powell算法的收敛条件确定。

当磁密幅值Bm=1.398T时，基于PSO算法的改进矢量Preisach模型平均绝对百分比误差随迭代次数的变化如图11所示。从图中可以看出，PSO算法具有较强的全局寻优能力，但局部搜索能力较弱。在其优化初期，仅需4次迭代便可使平均绝对百分比误差由 21.369 8%下降到 7.394 3%，收敛速度较快；但当迭代次数超过4次时，平均绝对百分比误差不再发生显著变化，收敛速度异常缓慢。另一方面，由于PSO算法在设定范围内随机选取初始值，因此，每次优化的平均绝对百分比误差收敛值不尽相同。上述两方面缺陷表明，该随机性优化算法在趋于全局最优解时，收敛性将大幅下降，难以准确高效地提取改进矢量Preisach模型参数的全局最优解。

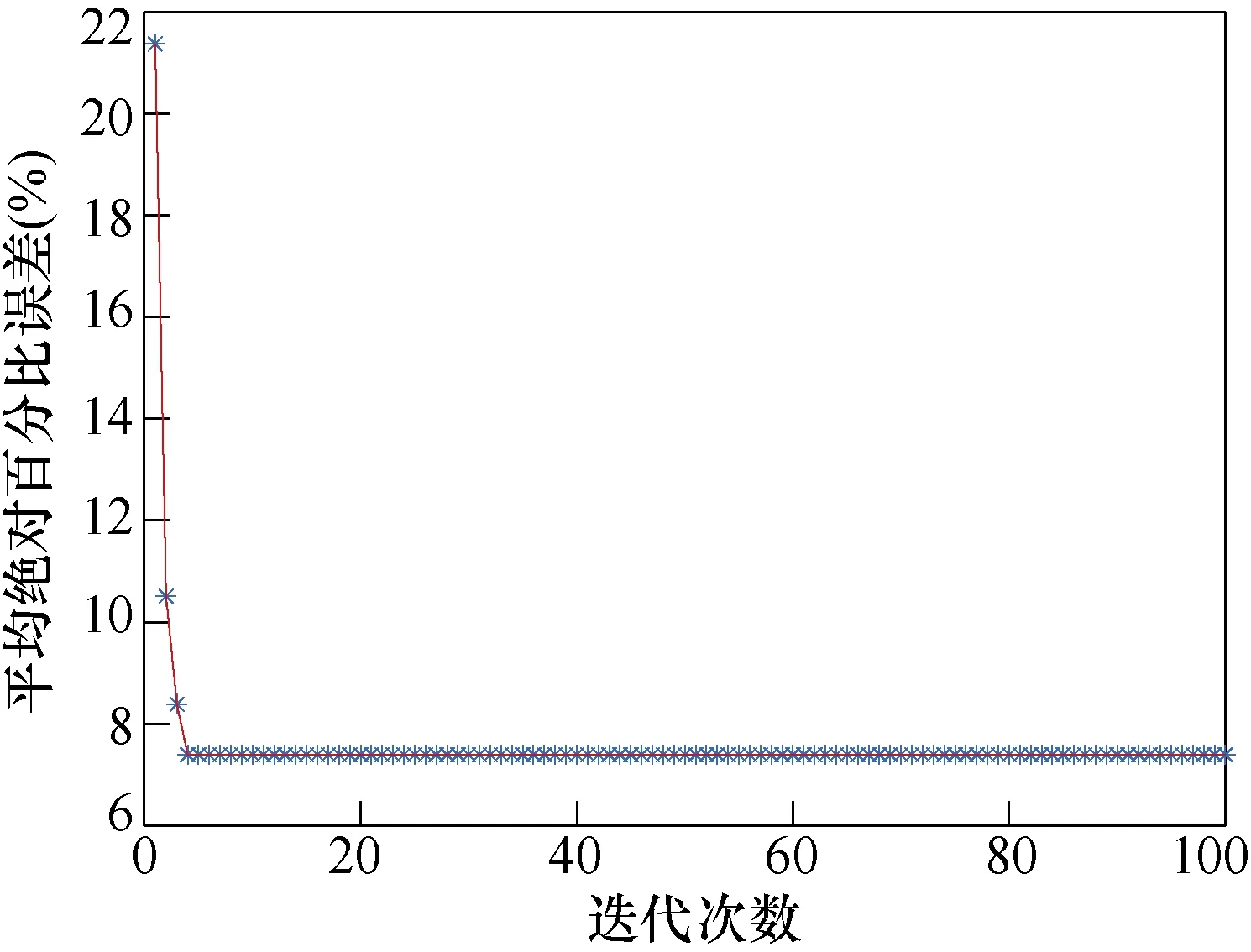
图11 PSO算法平均绝对百分比误差随迭代次数的变化Fig.11 MAPE variation with the iteration number based on PSO algorithm

表1给出了采用PSO算法在不同磁通密度幅值Bm下提取的模型参数及相应的平均绝对百分比误差与最大相对误差。根据表1所给模型参数拟合得到的二维矢量磁场强度H磁滞曲线与实测曲线比较如图12所示。从图中可以看出，当Bm=1.398T时，基于 PSO算法优化提取参数拟合结果与实验值产生了较大偏差，难以反映 SMC材料所呈现的部分各向异性特征。

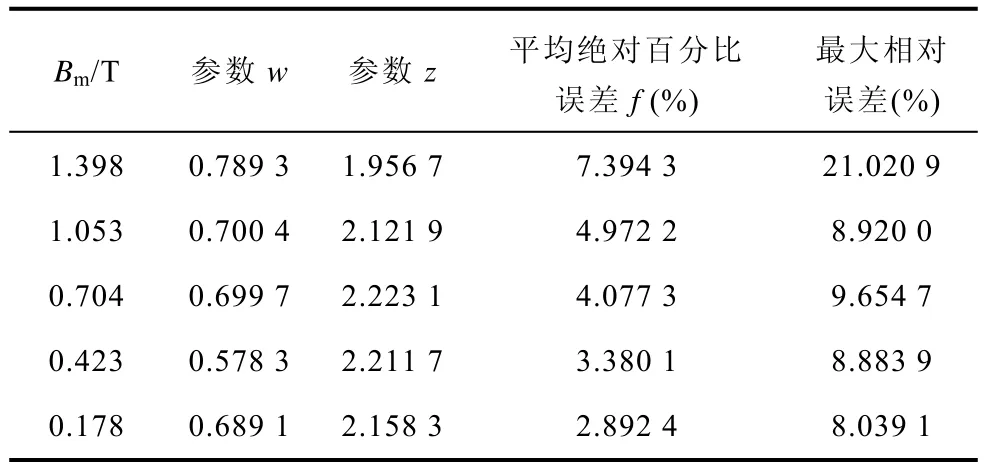
表1 PSO 算法参数提取结果及其误差Tab.1 The parameter values and corresponding error extracted by PSO algorithm

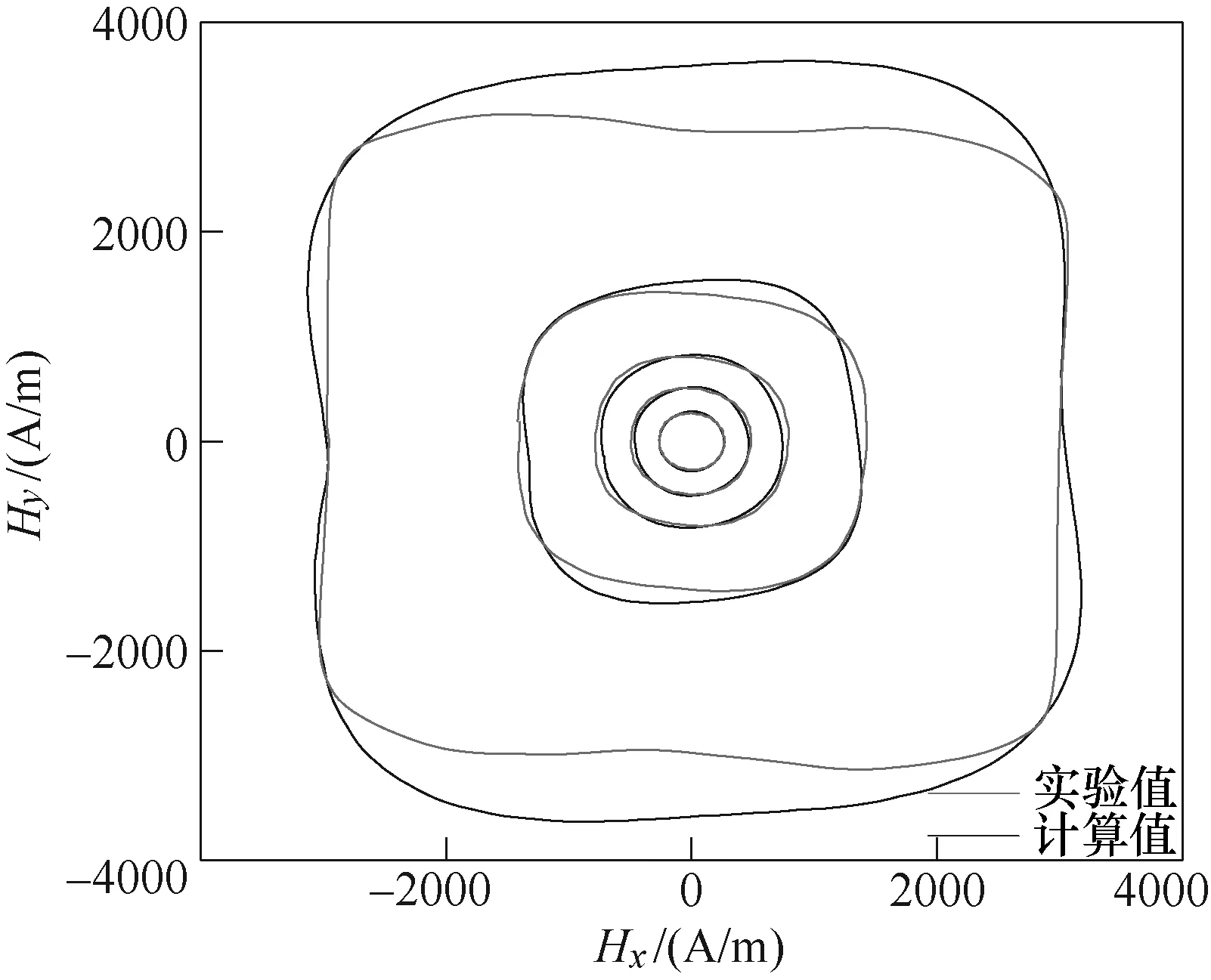
图12 基于PSO算法拟合H曲线与实测曲线比较Fig.12 Comparison between experimental H and simulated H based on PSO algorithm

基于PSO-Powell混合算法，给出了Bm=1.398T时改进矢量Preisach模型平均绝对百分比误差随迭代次数的变化情况，如图13所示。由图13a可知，在迭代前期，PSO算法达到 12次迭代时即自动满足算法的切换准则，而后Powell算法经过4次迭代即可满足收敛条件，如图13b所示。该现象说明混合算法比单一 PSO算法具有更快的收敛速度，其中，PSO算法能够快速锁定全局最优解所在区域，在自动满足切换准则后，Powell算法凭借其局部寻优能力，快速收敛于全局最优解。

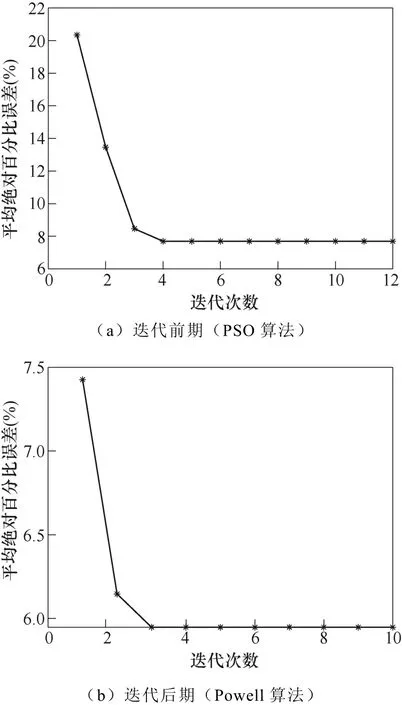
图13 PSO-Powell混合算法平均绝对百分比误差随迭代次数的变化Fig.13 MAPE variation with the iteration number based on hybrid algorithm of PSO-Powell

该混合算法所提取的改进矢量Preisach模型参数及其误差见表2。与表1对比可以看出，采用混合算法能够将平均绝对百分比误差控制在6%以内，同时使最大相对误差降至11%以下，有效降低模型误差，较单一PSO算法具有更高的求解精度。

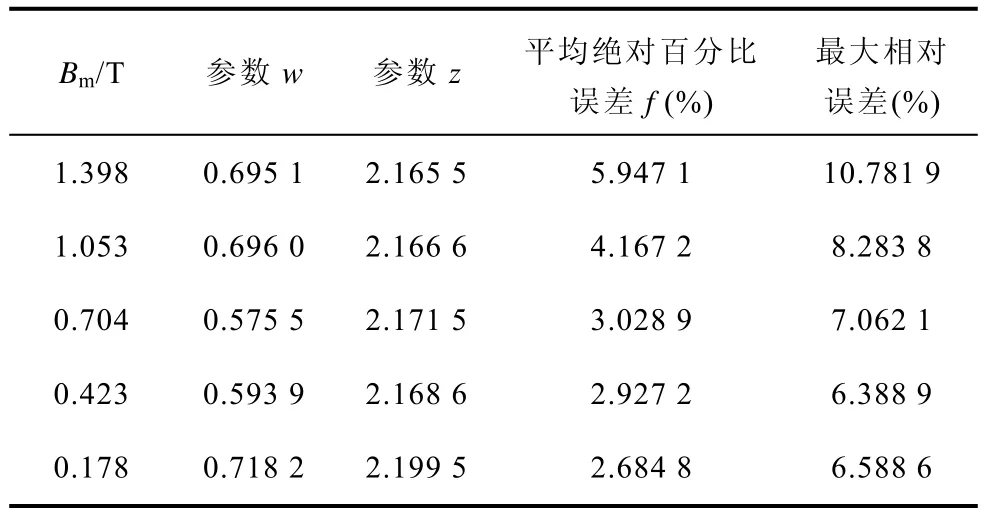
表2 PSO-Powell混合算法参数提取结果及其误差Tab.2 The parameter values and corresponding error extracted by hybrid algorithm of PSO-Powell

根据表2中PSO-Powell混合算法提取参数的二维矢量H磁滞曲线拟合结果如图14所示，由图可知，当圆形旋转磁通密度幅值Bm在大范围内变化时，拟合曲线与实测结果比单一PSO算法的拟合优化结果吻合更好，能够较好地反映样品的部分各向异性，从而验证了所提模型及其参数提取混合算法的准确性和高效性。

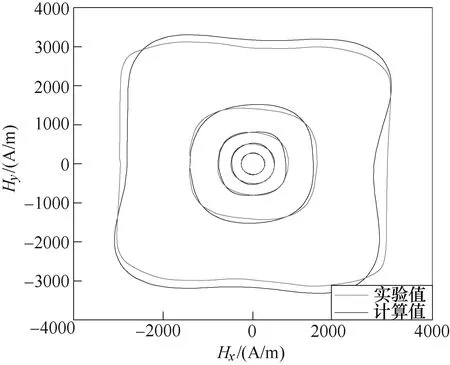
图14 基于PSO-Powell混合算法拟合H曲线与实测曲线比较Fig.14 Comparison between experimental H and simulated H based on hybrid algorithm of PSO-Powell

SMC材料磁滞回线的准确模拟有利于电气设备磁特性的有效分析。如图15所示，给出了Bm=1.398T工况下分别采用改进模型对旋转激励下该样品沿x、y方向磁滞回线的仿真结果，并与经典Preisach模型仿真结果及实测结果进行对比。由图15可知，所提改进模型仿真结果与实验结果吻合良好，较经典模型拟合结果更加准确，从而验证了所提方法应用于电气设备磁性材料磁化特性计算与分析的准确性。

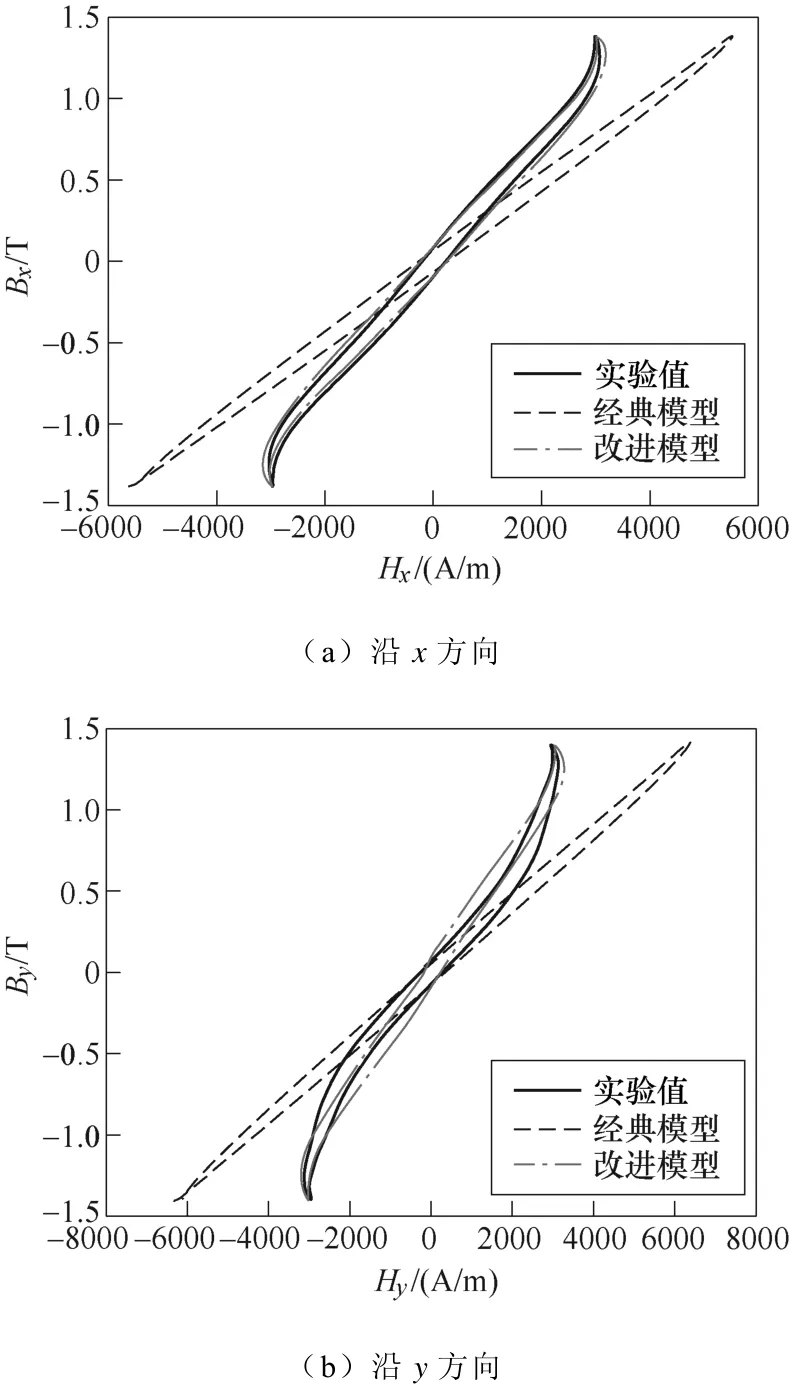
图15 Bm=1.398T磁滞回线测量与仿真比较Fig.15 Comparison between measured hysteresis loops with simulated ones at Bm=1.398T

混合算法提取模型参数拟合磁滞回线在磁密较高（超过1T）时略微存在误差[16,20]主要是由于实验测量方法的偏差，圆形旋转磁场激励下运动行为复杂，不仅有磁畴壁的平动，而且存在磁畴壁的转动，而测量过程中仅假设x、y两个方向独立的磁畴壁移动。因此，磁密越高，材料各向异性越明显，产生的测量偏差越大。另外，改进矢量模型在运用数值计算进行拟合曲线时亦能造成微小的误差。

4 结论

1）基于矢量磁特性测量平台，得到SMC材料的旋转磁特性，根据其各向异性特征，通过引入幅值与方向角的关联参数来改善磁场强度H的曲线形态，实现矢量磁滞模型的改进。

2）结合随机性优化算法全局搜索能力强以及确定性优化算法局部寻优能力强的优势，提出 PSO-Powell混合式优化算法，显著改善参数局部寻优能力，提高了计算效率和计算精度。

3）将旋转磁特性的测量结果与仿真结果相比较，二者较为一致，验证了本文所提改进矢量磁滞模型及其参数辨识过程中混合优化策略的有效性。