测力刀柄系统标定技术研究

吴凤和, 张 宁, 李元祥, 郭保苏

(1. 燕山大学 机械工程学院,河北 秦皇岛 066004;2. 河北省重型智能制造装备技术创新中心,河北 秦皇岛 066004)

1 引 言

智能制造是新一轮工业革命的主攻方向,智能生产是智能制造的主线[1],实现切削状态的在线监测是实现智能生产的先决条件。切削力作为切削过程中最为稳定也最易获取的重要参数之一,可为研究刀具磨损状态监测、颤振监测与抑制、加工表面质量预测等在线监测提供重要的数据,并进而实现刀具参数优化设计、切削参数优化等目的。因此,很多专家学者对切削过程中切削力的测量方式进行研究,并设计了多种结构类型的测力装置。目前,板式测力仪以测量精度高、设计制造方便等特点,成为最常用的切削力测量装置,但由于板式测力仪的安装面板对工件的尺寸和重量有限制,且易受到切削液长期浸溅而造成表面腐蚀,所以常常仅限于实验室使用,不适用于生产加工过程中力的测量。因此,许多学者尝试将传感器集结在刀柄或主轴上以实现切削力的测量。Totis等[2]将三向力传感器安装在可转位刀片下方进行力信号的感知,可实现每个刀齿的切削力测量;Suprock等[3]在刀具上集结了多类型测量传感器,实现了力、扭矩和温度的监测;Rizal等[4]研制了一种应用弹性梁结构的应变式三维测力刀柄系统。

测力装置在使用前需通过实验建立输入量(载荷)和输出量(电信号)之间的关系及规律,该过程称之为标定。标定又可细分为静态标定和动态标定。在静态标定方面,王宇飞等[5]研制了可直接在车床上对车削测力仪进行在机标定的标定装置,其通过砝码杠杆式原理进行静态加载;付立悦等[6]针对自行设计的六维力传感器,搭建了静态标定系统,通过定滑轮和标准砝码进行六维力加载;张强等[7]设计了一种仿生指尖三维力传感器,并针对其研制了一套静态标定装置,该装置采用L型支架结构,通过加载砝码的方式进行标定实验。Xie等[8]将刀柄安装在机床上进行静态标定,通过刀柄压向标准测力仪的方式实现轴向加载,通过在刀柄两侧等距位置施加反向力的方式实现扭矩加载,但该标定过程易因杆件变形导致力臂变化,使扭矩加载不准确。虽然上述静态标定装置针对特定传感器可获得良好的标定效果,但对于测力刀柄而言,均难以实现刀柄的稳定夹持与准确加载,同时砝码的加载量程较小无法满足测力刀柄的标定要求。在动态标定方面,张乾斌等[9]设计了基于水平正弦力加载的力传感器动态标定装置,通过偏心轮离心原理对被测装置施加正弦激振力,进而获得动态特性曲线;郑红梅等[10]设计了一种动态标定实验台,通过剪断细绳突然释放砝码,从而给传感器施加阶跃激励的方式测试机器人六维腕力传感器的动态性能。

本文测力刀柄的动态标定主要关注其工作条件下的固有频率,因此,需将刀柄安装在机床上进行测试,正弦激励法和阶跃响应法均需复杂的实验装置,在测力刀柄的实际工况下难以进行激振力的施加。本文针对自主设计的测力刀柄系统,根据其整体结构和工作原理,研制了一套标定辅助工装,研究了轴向力和扭矩的标定加载方式,搭建了测力刀柄系统的静、动态标定实验平台;基于标定实验,确定了测力刀柄系统的静态及动态特性指标;最终通过实际钻、铣削测量实验验证了系统的可行性和准确性。

2 测力刀柄系统标定原理

2.1 测力刀柄系统结构及其工作原理

自主设计的测力刀柄系统[11]如图1所示,系统以电阻应变式传感器为感知元件,传感器感知的信号经过采集、传输后,以无线的形式发射出去,上位机终端进行数据的实时接收、处理以及切削力信号的可视化。整个采集传输过程(电阻应变传感器、采集、传输模块)需用电源模块供电。测力刀柄整体结构如图2所示,其中,传感器粘贴在刀柄的环形槽内,通过屏蔽线穿过电路半载体的矩形孔与信号采集传输模块相连通;轴向力和扭矩测量传感器各通过一组信号采集传输模块与电源模块实现工作以及输出信号的采样与发射;考虑到信号采集传输模块与电源模块质量不等,将4个模块交错放置,并分别通过两个夹具固定在半载体上,以保证系统的动平衡;两个电路半载体通过2个预紧螺钉夹持固定在刀柄基体上,且在外侧套装一个密封罩实现传感器、信号采集传输模块等元件与外界的隔绝保护;装配后传感器、信号采集传输模块、电路载体等所有元件可以随刀柄基体在主轴上一同旋转;最终,信号接收装置可以接收刀柄基体上发射出的Wi-Fi信号并通过网线传输至上位机实现轴向力和扭矩数值的实时显示。

图1 测力刀柄系统组成图Fig.1 Composition of force measuring tool holder system

图2 测力刀柄结构示意图Fig.2 Schematic diagram of force measuring tool holder system

与传统板式测力仪相比,测力刀柄将力感知功能和零件切削功能进行了集成,在切削加工过程中可同时实现切削力的测量,克服了传统测力装置限制工件尺寸,易受切削液腐蚀的缺陷,具有更高的灵活性和可移植性,而其技术性能指标需要通过标定实验来确定。

2.2 静态标定实验原理

静态标定[12]是指通过对被测对象输入不随时间变化的或变化十分微小的信号,获取到系统输出信号,并可以建立输入信号与输出信号之间关系的实验。对于测力刀柄系统而言,通过对其分别加载轴向力和扭矩,并获取系统中电阻式传感器在对应载荷下的输出电压值,进而建立载荷与输出电压之间的函数关系。通过建立的函数关系,可以在未来应用中根据系统输出电压值进而推算出系统所承受的未知载荷大小。通过静态标定实验,可以获得系统的非线性误差、重复性误差、滞后误差、相间干扰误差、灵敏度和分辨率等各项性能指标。

1) 非线性误差

测力刀柄系统理想的输出与输入是线性关系,而实际输出值与输入严格来讲是非线性的,存在一定误差,如式(1)所示。

(1)

式中:Δmax为标定过程中实际曲线偏离理论直线的最大值;YFS为标定过程的最大输出值。

2) 重复性误差

测力刀柄系统在输入上按同一方向作全量程连续多次测试时所得输入-输出特性曲线不重合度,如式(2)所示。

(2)

式中ΔyRM为同一输入量按同一方向变化所对应输出量的最大差值。

3) 滞后误差

测力刀柄系统在一次加载与卸载过程中输入-输出特性曲线的不一致性,如式(3)所示。

(3)

式中ΔyHM为一次加载与卸载过程中同一载荷下所对应输出量的最大差值。

4) 向间干扰误差

测力刀柄系统在某一特征方向施加输入量,而在其它方向(横向)产生输出量称为向间干扰误差,如式(4)所示。

(4)

式中:ΔyCM为某方向加载过程中在其他方向上产生的输出量值；YFSA为在其他方向上的满量程输出量值。

2.3 动态标定实验原理

动态标定[13]是指通过对被测对象输入随时间变化的动态力而获取其输出响应(频率响应,时间相应)特性的实验。考虑到在同一切削参数下,不同结构或者类型的切削力测量装置测量的动态切削力结果可能大不相同,这是由于其与测量装置的动态特性具有密切联系。因此,测量装置不仅要经过静态标定获取其静态性能,还需要经过动态标定获取其动态性能,以确定测量装置的应用范围。

动态标定后可获得被测装置的动态特性曲线,一般包括幅频特性曲线、相频特性曲线或“增益-频率”特性曲线。通过对特性曲线分析可获得测量装置的固有频率ωn、最大允许工作频率ωmax、阻尼比ξ和相位差φ等动态特性。对于测力刀柄系统来说,其需要在一定的切削频率下准确测得切削过程中的轴向力和扭矩数值。因此,获取其固有频率ωn、最大允许工作频率ωmax十分必要。

3 测力刀柄系统标定实验平台

3.1 静态标定实验平台

测力刀柄系统属于大量程测力装置,其轴向力和扭矩方向的设定量程分别为±2 000 N和 ±100 N·m,传统的砝码式加载难以达到标定要求。考虑到刀柄的实际工况,本文选择万能试验机和扭转试验机作为轴向和扭矩方向的静态标定加载装置。静态标定实验对标定装置的要求为：标定装置的测量精度要比被标定物的测量精度高一个数量级或者标定量的分辨率至少为1/3,方能保证标定结果的准确性,并且,在标定时需要对被标定物进行满量程载荷值的110%～120%数值大小进行预加载。综合考虑标定装置的测量精度和量程两方面因素,分别采用WDW-100型万能试验机和ND-500型扭转试验机作为标准载荷加载装置用于系统的轴向力和扭矩标定,具体参数如表1所示。

表1 标定装置系统参数Tab.1 Parameters of calibration device system

测力刀柄系统在工作时,其锥柄端与机床主轴相连,夹套端与刀具相连,为使标定结果更接近真实工作条件,本文设计了如图3所示的静态标定辅助工装,其中,工装1模拟机床主轴,其法兰盘沿周向均布2个键槽,并通过平键实现与刀柄的周向固定;工装2模拟刀具,其安装在ER32弹性夹套内部,并通过夹套螺母实现与刀柄基体的周向紧固。扭转试验机夹持工装1和工装2的外圆柱表面,对刀柄进行扭矩加载。

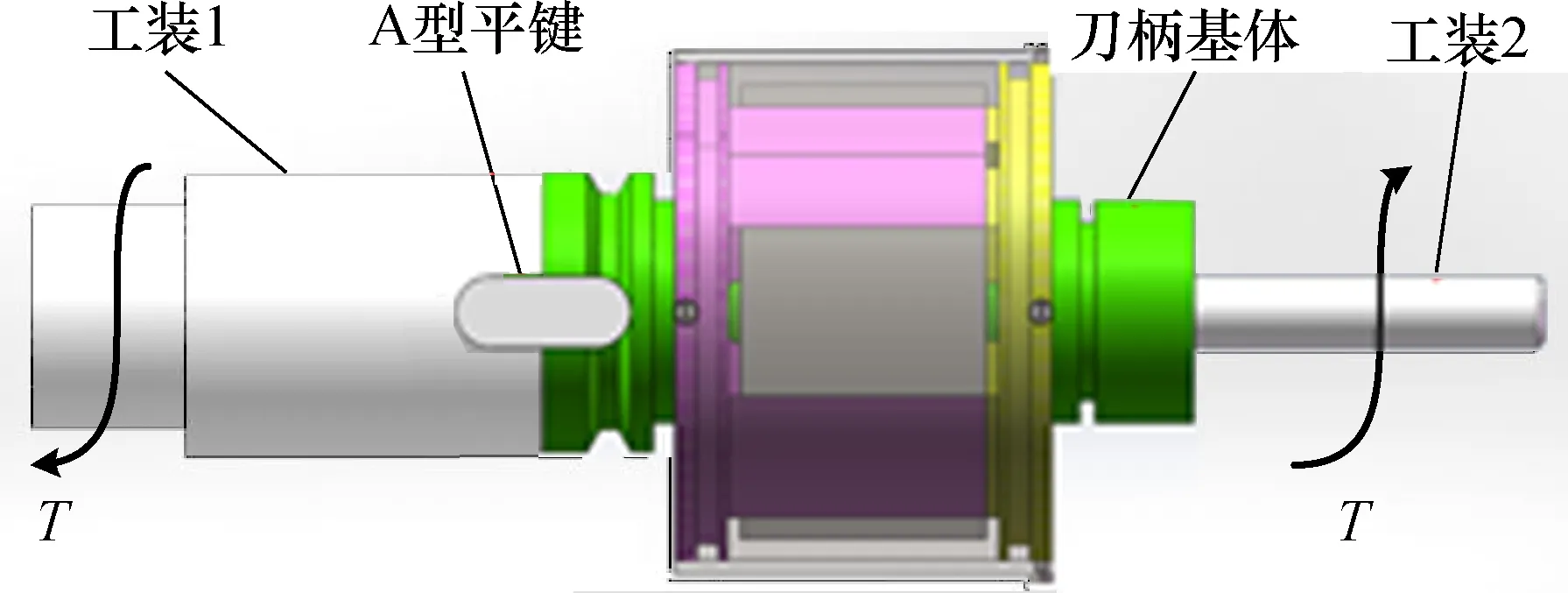
图3 静态标定辅助工装Fig.3 Static calibration auxiliary tooling

为保证标定过程中轴向力加载的准确性,避免刀柄轴线与刀柄在试验机上的安装平面不垂直导致产生其他方向上的分力,进而产生标定系统误差,通过调节刀柄在试验机安装面所在的球铰位置,保证轴线与安装平面的垂直度误差不大于0.03 mm;为保证标定过程中扭矩加载的纯粹性,避免施加轴向力进而产生人为因素形成的横向误差,将图3中的辅助工装1与刀柄在轴线上保持一定间隙,以防与试验机固连的辅助工装对刀柄施加轴向载荷。最终轴向力和扭矩的静态标定实验平台如图4和图5所示。

图4 轴向力标定实验装置Fig.4 Calibration device of axial force

图5 扭矩标定实验装置Fig.5 Calibration device of torque

3.2 动态标定实验平台

不同的约束条件会对被测物体的自振频率产生影响,为尽可能的模拟系统在工作时的固有频率,将测力刀柄系统安装在机床主轴上进行动态标定。动态标定采用脉冲激励法,并选用LC02A型号模态冲击锤(配备CL-YD-312型号压电力传感器)作为冲击力发生装置(即信号输入装置),DH311型号三轴压电式加速度传感器作为系统振动采集装置(即信号输出装置),DH8300型号动态信号测试分析系统作为输入-输出信号分析装置。

受限于刀柄结构,在扭矩方向动态标定时难以直接通过力锤对刀柄施加瞬态切向力,因此,本文设计了如图6所示的动态标定辅助工装。实验时,工装圆柱部分夹持在弹性夹套中,通过敲击与刀柄轴线平行的侧向端面对刀柄施加切向力Ft,并借助尺寸为a力臂将其转化为扭矩T。最终搭建的动态标定实验平台如图7所示。

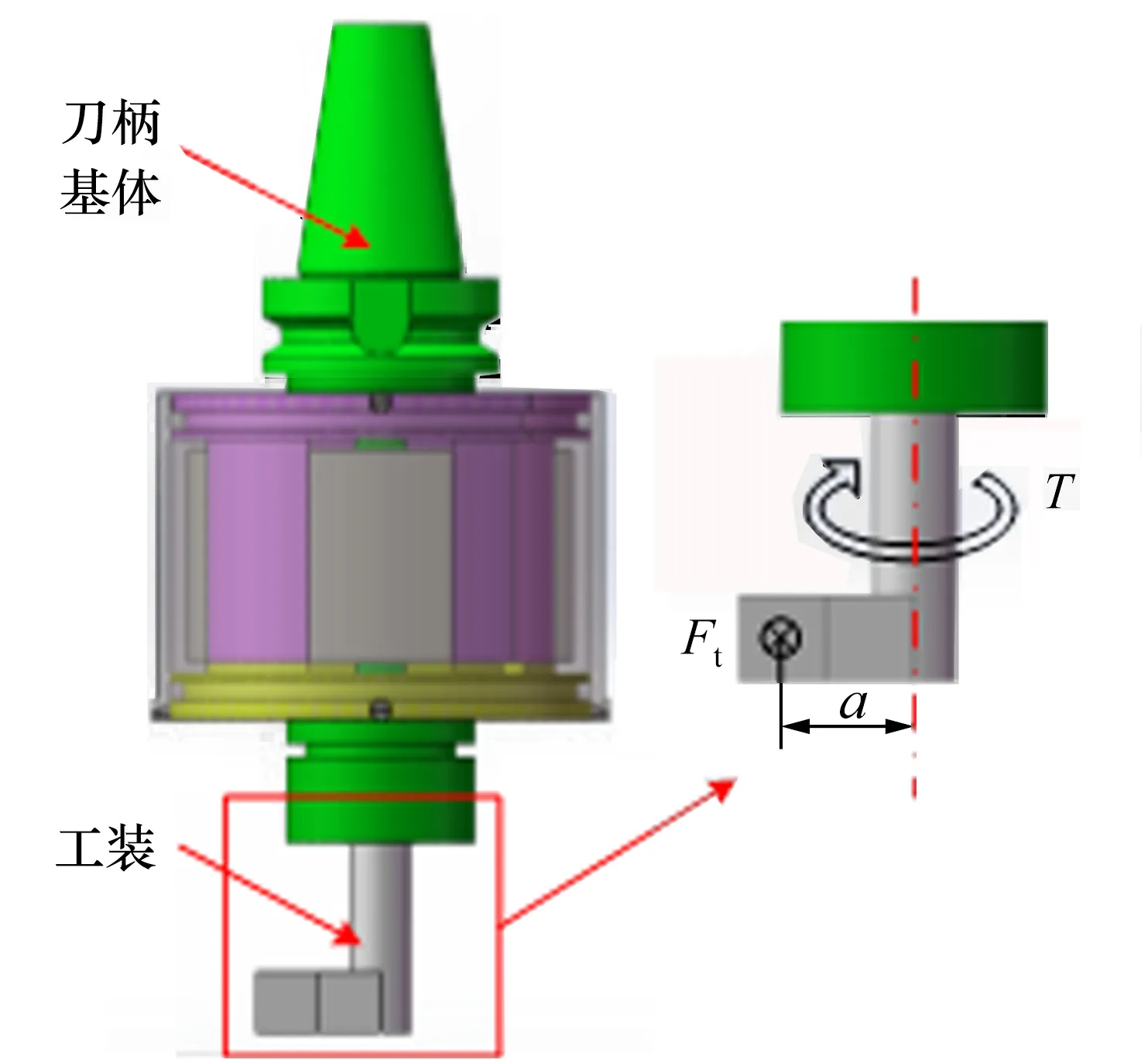
图6 动态标定辅助工装Fig.6 Dynamic calibration auxiliary tooling

图7 动态标定实验平台Fig.7 Dynamic calibration experiment platform

4 标定实验及数据处理

4.1 静态标定

在搭建的静态标定实验平台上,采用逐级加、卸的方式进行标定。加、卸载标定之前,首先对系统进行设定量程的110%数值大小加载,即加载2 200 N轴向力和110 N·m扭矩,反复4次,充分释放集结于刀柄基体的测力传感器经制作完成后的弹性;然后根据量程分别对轴向力以200 N和扭矩以10 N·m为一个加载步进行加载,直至加载到轴向力设定量程2 000 N和扭矩100 N·m,再逐级卸载,每个加、卸载步完成后保持载荷10 s,用于记录系统的输出电压值;最终,重复加、卸载3次,并记录。

根据轴向力和扭矩重复加、卸载3次实验数据,计算每个加、卸载步在保持设定载荷值下停留10 s的输出电压平均值,并以该平均值作为对应载荷下系统输出电压值,采用最小二乘法对数据进行拟合,得到了静态标定曲线方程及相间干扰曲线方程,分别如式(5)和式(6)所示,并绘制了如图8所示的轴向力和扭矩方向静态标定曲线。

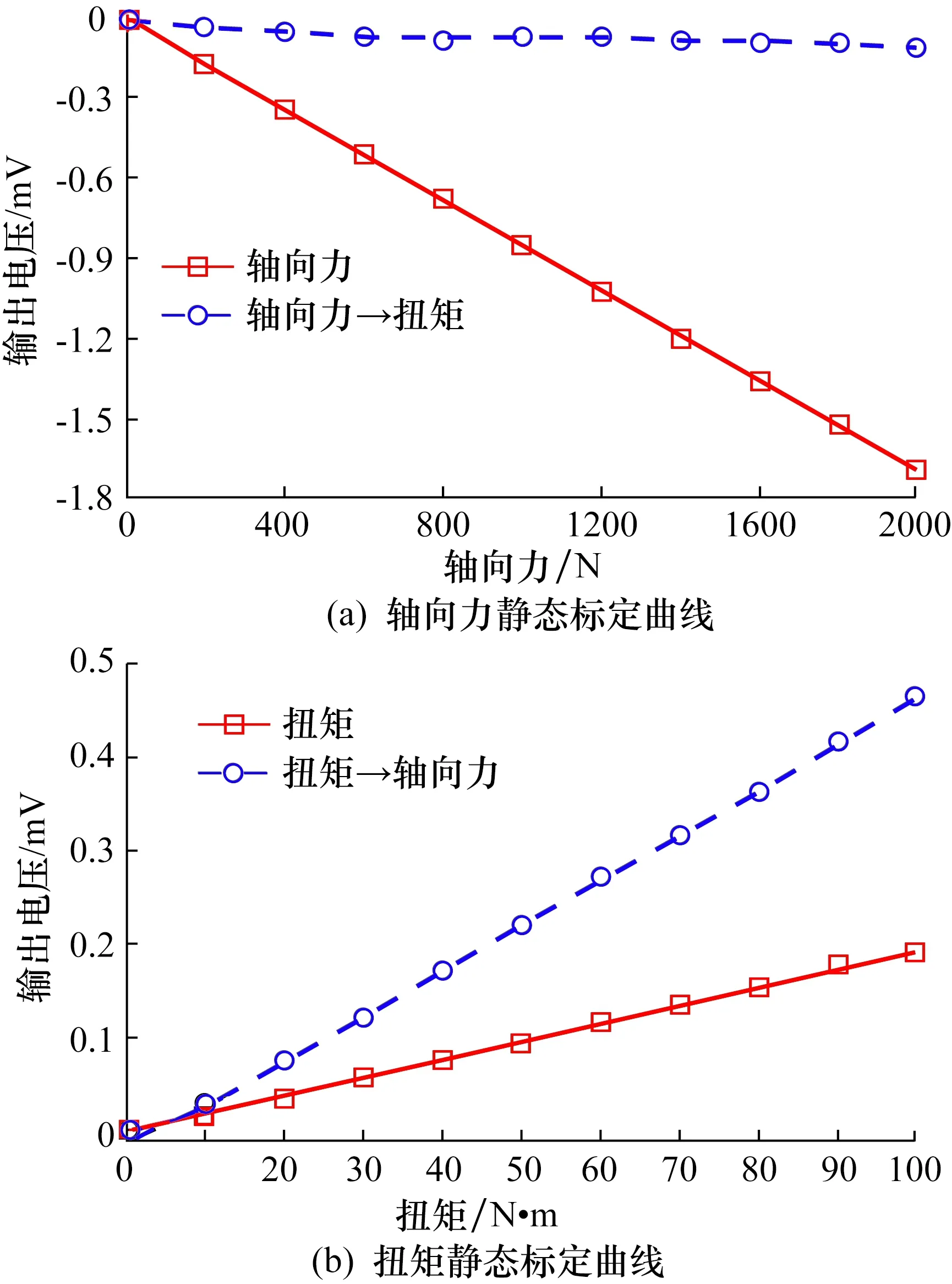
图8 轴向力和扭矩的静态标定曲线Fig.8 Dynamic calibration experiment platform

(5)

(6)

式(5)和式(6)中Fp为轴向力;T为扭矩。

根据曲线分析可得轴向力对扭矩的横向干扰为1.22%,扭矩对轴向力的干扰达30.35%。因此,直接采用输出电压值数据作为最终测量结果会导致轴向力结果的不准确,需要对轴向力和扭矩测量过程中的数据耦合进行分解,以保证系统测量的数值与实际切削过程中的数值相一致或者尽可能一致。系统实测的轴向和扭矩输出电压值ΔUaF,ΔUaT与对实际加载的轴向力和扭矩值Ftp,Tt测量时存在式(7)所示关系:

(7)

式中:aFF、aTT分别为轴向力Fp和扭矩T的测量灵敏度;aFT、aTF分别为轴向力Fp对扭矩T和扭矩T对轴向力Fp的相间干扰系数;btF、btT分别为轴向力值和扭矩值为0时轴向力和扭矩测量电路的输出电压值,其数值可由式(5)和式(6)所得。

为便于计算,将式(7)改写成矩阵形式,如式(8)所示。依据克莱姆法则对其进行求解可得如式(9)所示的解耦后切削力实际加载值方程。

(8)

(9)

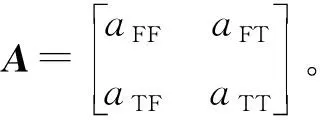
根据式(9)所示方程对静态标定结果进行解耦分析,得到解耦后的轴向力对扭矩的相间干扰误差下降至0.53%,扭矩对轴向力相间干扰误差下降至3.02%。最终,可得表2所示测力刀柄系统在轴向力和扭矩方向上测量的各项静态性能指标。其中,系统各项测量误差均小于5%,符合测力传感器的设计要求。

表2 测力刀柄系统的静态特性指标Tab.2 Static characteristic of the force measuring tool holder system

4.2 动态标定

依托搭建的动态标定实验平台,通过冲击力锤在垂直于刀柄基体底端面的中心位置敲击,产生瞬态轴向力,重复进行3次,获取3次敲击的输入-输出特性曲线;针对扭矩标定实验,通过敲击辅助工装侧向端面,产生瞬态切向力,进而对刀柄施加瞬态扭矩,重复进行3次并得到输入-输出特性曲线。

通过对系统进行轴向和扭矩方向的动态标定,获取如图9所示的动态特性曲线。分析曲线可知,测力刀柄系统在轴向方向的一阶固有频率为375 Hz,在扭转方向上的一阶固有频率为453.75 Hz,取两者最低值作为系统的一阶固有频率ωn=375 Hz。根据式(10)可得系统的阻尼比ξ=0.01,幅值相对误差ε=0.125以及最大工作频率ωmax=125 Hz。

图9 动态特性曲线图Fig.9 Dynamic characteristic curve

(10)

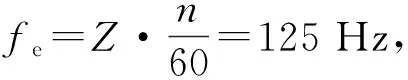
5 切削实验验证

测力刀柄系统在切削过程中的具体测量性能如何,需要通过切削实验进行验证。对于实际切削过程,切削力影响因素众多,无法通过理论公式进行精准计算,只能通过对比高精度参照测力仪的测量结果用于评判实测效果。

考虑到目前测力仪行业,Kistler公司的产品凭借其高测试精度和高稳定性被业内所普遍认可,本文选用Kistler9257B型号板式测力仪作为参照测力仪,其技术指标如表3所示,以XK714D型号三轴立式加工中心作为切削机床,工件材质为45#钢,刀具是材质为HSS的16 mm直柄5齿立铣刀,螺旋角为42°。最终搭建了如图10所示的切削实验平台。

表3 Kistler测力仪主要技术参数Tab.3 Main technical parameters of Kistler dynamometer

图10 切削实验平台Fig.10 Cutting experiment platform

切削时,将待加工工件与板式测力仪通过M8×16螺栓固连,然后将测力仪安装在机床工作台上。通过Kistler9257B板式测力仪与测力刀柄系统同时采集切削过程中的轴向力与扭矩信号。每组切削参数切削工件3次,取其平均值作为该切削参数下的轴向力和扭矩测量结果。

当切削转速n=1 250 r/min,每齿进给量fz=0.016 mm,切削宽度ae=15 mm,切削深度ap=0.3 mm时,测力刀柄系统和Kistler测力仪测量的轴向力和扭矩波形图如图11所示。

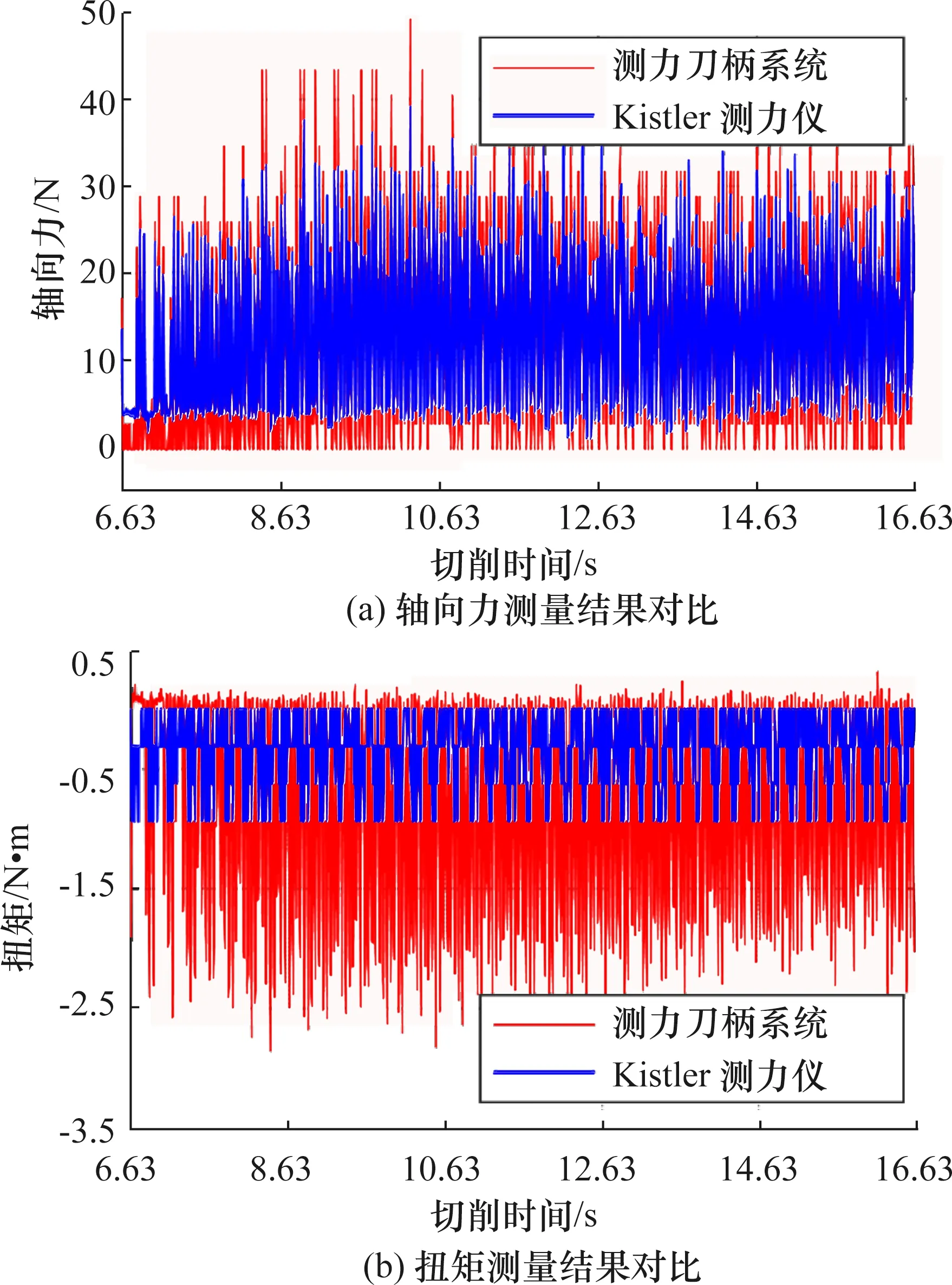
图11 测力刀柄系统与Kistler 测力仪铣削测量结果对比Fig.11 Comparison of milling measurement results between tool holder system and Kistler dynamometer

经分析可得,在轴向力方向上刀柄系统测量结果均值为13.552 1 N,Kistler测力仪测量结果的均值为13.313 5 N,其偏差为1.79%;而扭转方向上刀柄系统测量结果均值为-0.336 4 N·m,Kistler测力仪测量结果均值为-0.822 9 N·m,差值极大。

对该参数下刀柄系统测量的扭矩数据进行幅频特性分析,获取其幅频特性曲线如图12所示。通过幅频特性曲线可知,主轴的转动频率为20.8 Hz,铣刀的切削频率为104.3 Hz,低于刀柄系统的最大工作频率,符合正常切削要求,表明该切削参数下的刀柄系统动态性能表现正常,测量结果可信。因此,扭矩方向上出现较大偏差在很大程度上是由于参照测力仪导致的。

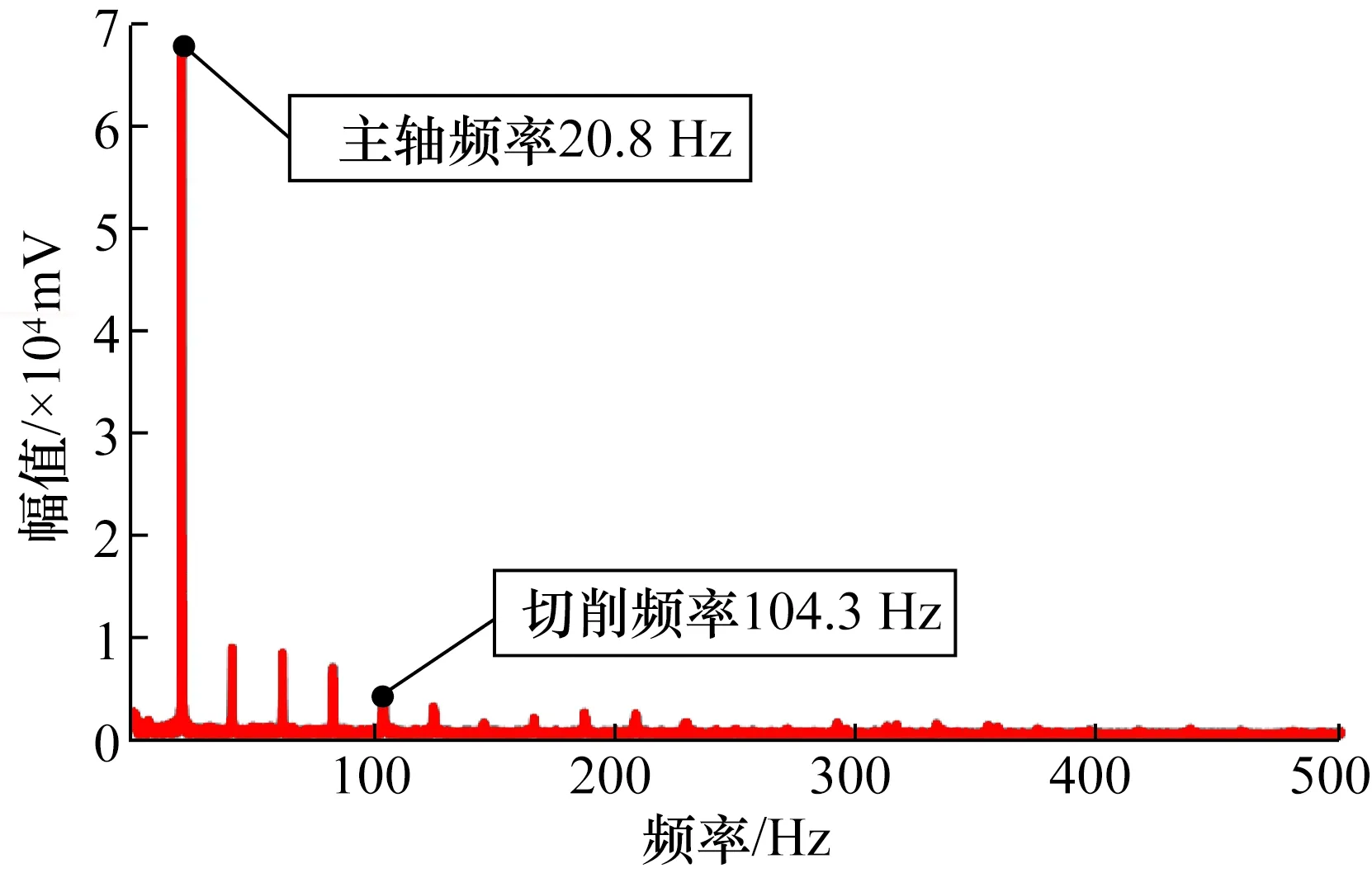
图12 轴向铣削力信号的幅频特性曲线Fig.12 Amplitude frequency characteristic curve of axial force signal

Kistler 9257B型号板式测力仪的结构简图如图13所示,其通过4个三维力传感器的信号合成实现六维力的测量,其中轴向力和扭矩的测量原理如式 (12) 所示:

图13 Kistler测力仪测量原理示意图Fig.13 Schematic diagram of measurement principle of Kistler dynamometer

(12)

式中:FZ1、FZ2、FZ3、FZ4分别为1～4号传感器测得的Z向力值;FX12是1、2号传感器测得的X向合力值;FX34是3、4号传感器测得的X向合力值;FY14是1、4号传感器测得的Y向合力值;FY23是2、3号传感器测得的Y向合力值;a、b分别为传感器中心距测力仪面板中心在X和Y向的距离。

由式(12)可知,参照测力仪在测量扭矩时,只有切削点位于面板中心位置点A时方可保证扭矩测量的准确性。但是在铣削过程中切削点B是随时间不断变化的,所以参照测力仪在上述铣削过程中测量的扭矩偏差较大。因此,刀柄系统与参照测力仪在扭矩方向上测量结果偏差较大是由于参照测力仪测量结果的不精确性导致的。

为评判测力刀柄系统在扭矩方向上测量结果的性能,设计了多组钻削实验,实验过程中将切削点位于参照测力仪面板中心位置A点上,采用材质为HSS的16 mm直柄麻花钻,螺旋角为30°,顶角为135°。当切削转速n=500 r/min,进给速度vf=50 mm/min时,测量结果如图14所示。

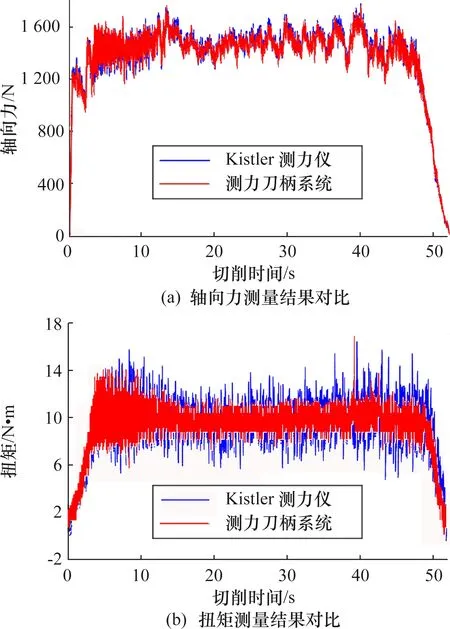
图14 测力刀柄系统和Kistler测力仪第1组钻削测量对比Fig.14 Comparison of drilling measurement between the first group of Kistler force measuring instrument and the force measuring tool handle system

在轴向力方向上,刀柄系统测量结果均值为1 355.7 N,Kistler测力仪测量结果均值为1 365.4 N,其偏差为0.7%;在扭矩方向上,刀柄系统测量结果均值为 9.015 N·m,Kistler测力仪测量结果均值为9.173 5 N·m,其偏差为1.73%。当切削转速n=600 r/min,进给速度vf=50 mm/min时,测量结果如图15所示,在轴向力方向上,刀柄系统测量结果均值为1 113.0 N,Kistler测力仪测量结果均值为1 114.3 N,其偏差为0.12%;在扭矩方向上,刀柄系统测量结果均值为 7.906 4 N·m,Kistler测力仪测量结果均值为 7.412 2 N·m,其偏差为1.02%。

图15 测力刀柄系统和Kistler测力仪第2组钻削测量对比Fig.15 Comparison of drilling measurement between the second group of Kistler force measuring instrument and the force measuring tool handle system

结果表明,测力刀柄系统与参照测力仪在测量结果上具有良好的一致性,即该系统测量精度高,可用于实际生产加工中切削力的测量。

6 结 论

针对测力刀柄系统的特殊结构和工作原理,设计了一套标定辅助工装,搭建了测力刀柄系统标定实验平台。采用逐级加、卸载法获得了系统线性误差、重复读误差、滞后误差、相间干扰、灵敏度和分辨率等静态指标,并针对相间干扰误差较大的情况进行误差补偿,补偿后的误差大大减小,静态性能误差均在5%以内;基于脉冲激励法获取了系统在轴向和扭转方向的固有频率、工作频带和阻尼等动态指标,结果表明系统动态特性可以满足切削使用要求;完成切削实验,分析了铣削时扭矩测量与Kistler测力仪产生较大偏差的原因,从原理上证明测力刀柄在扭矩测量中更加精准,进一步进行了钻削实验,表明系统与参考测力仪的测量偏差在轴向和扭矩方向上均小于2%,满足使用要求。