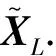矩阵方程X+A*X-2A=I极大解的扰动分析

马 伟，高景利

(南阳师范学院 数学与统计学院，河南 南阳 473061)

在控制论、梯形网络分析、统计学、动态规划等很多领域，经常会出现非线性矩阵方程

X+A*X-2A=I,

(1)

其中,A是n阶非奇异复矩阵，I是n阶单位矩阵.在本文中，我们主要讨论该方程的Hermite 正定解.

最近已有很多学者[1-8]对方程(1)进行了研究.文献[1-3,7]中提出了Hermite 正定解的存在条件及迭代计算法.文献[4]讨论了更一般的方程

Xs+A*X-tA=I,

其中s，t是自然数，利用不动点原理得出了此方程的一个正定解存在条件并提出了三个计算正定解的迭代方法.文献[5-7]中给出了矩阵方程(1)的Hermite正定解的一些扰动界.

在本文中，我们利用初等微积分给出了方程(1)的新扰动界，分析新扰动界的优势，并用数值例子与已有结果进行了比较说明.

1 扰动界

我们首先给出文献[5]中关于矩阵方程X+A*X-2A=I的一些关于扰动界的结论.

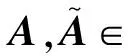
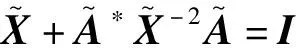
(2)

其次，文献[6]给出了矩阵方程X+A*X-nA=P的极大解的扰动界，Hassanov 和Ivanov在文献[7]中矩阵方程X±A*X-nA=Q的极大解的扰动界.特别地，当n=2，P=I，Q=I时，他们给出以下两个定理.

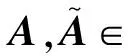
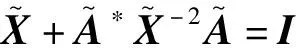
(3)

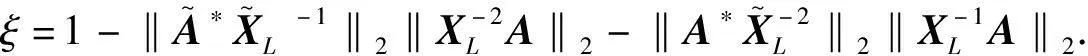
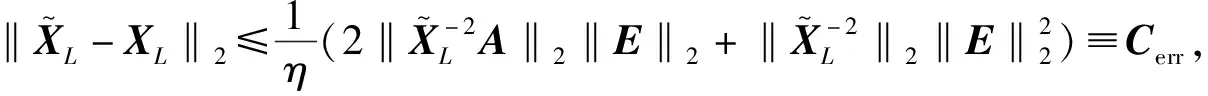
(4)

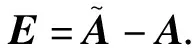
下面，利用文献[4]的一些结论以及初等微积分的知识，得到矩阵方程(1)的极大解的一个新扰动界.

对于下列多项式方程

x3-x2+λmin(A*A)=0,

(5)

x3-x2+λmax(A*A)=0.

(6)

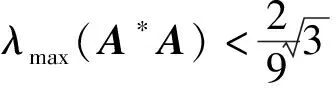
(7)

引理1[4]设A∈n×n，并且则

(a)矩阵方程(1)在[α1I,α2I]上有Hermite正定解；

(b)矩阵方程(1)在[β1I,β2I]上有唯一的Hermite正定解；

(c)矩阵方程(1)在[α2I,β1I]上没有Hermite正定解.

备注1我们称矩阵方程(1)在[β1I,β2I]上有唯一的Hermite正定解为极大解，记为XL.

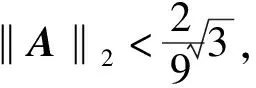
(8)

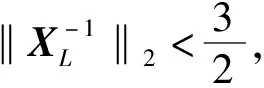
(9)

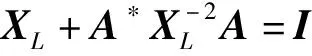
(10)

(11)

对(11)式两端取酉不变范数，

(12)

又因为

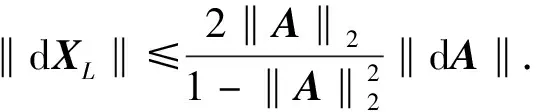
根据引理2可得矩阵方程(1)的极大解的如下扰动界.

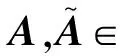
(13)

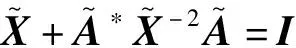
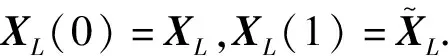
由奇异值的扰动定理可得

‖A(t)‖2≤‖A‖2+‖E‖2t，

从而

另外，根据定理4，可得如下推论.

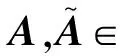
2 数值举例

本节举例验证前面我们所给的结果.其所有的计算都在精度为ε=2.2×10-16的计算机上用Matlab 2010b来完成.

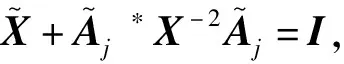
表1